1. Introduction

The infestation of pests such as fruit borers severely affects the growth of Rosa roxburghii, leading to a significant decline in its yield [1]. Traditional pest control methods that rely on manual spraying or mechanical equipment are not only labor-intensive and inefficient, but also result in substantial pesticide waste. Moreover, these approaches expose operators to the risk of pesticide poisoning, making them inadequate for large-scale cultivation [2]. Plant protection Unmanned Aerial Vehicles (UAVs) [3], with their advantages in agility, intelligence, and low carbon emissions, overcome the limitations of terrain and manual labor. They enable fast and precise operations, thereby greatly enhancing the efficiency and safety of agricultural pest control.

In the practical application of plant protection UAVs, determining an efficient and rapid path planning method is crucial to ensuring high-performance operation. Currently, mainstream path planning algorithms can be categorized into global path planning and local path planning. Local path planning refers to methods that utilize onboard sensors to detect environmental information in real time and generate a feasible path when only partial information about obstacles is available. Liu et al. [4] proposed a UAV Dynamic Path Planning Algorithm (UAV-DPPA-DWA) based on the integration of the dynamic window approach. By improving the elliptical tangent graph algorithm and adopting an adaptive obstacle avoidance strategy, their method significantly enhanced the UAV’s obstacle avoidance capability and task efficiency in complex dynamic environments. Zhang et al. [5] combined a Genetic Algorithm (GA) with an improved Rapidly-Exploring Random Tree (RRT) algorithm to successfully generate high-quality, collision-free paths for multi-objective planning in complex man-made forest areas. Yang et al. [6] integrated the multi-objective path planning algorithm MI-RRT* with an enhanced dynamic window approach, substantially improving robotic inspection efficiency in intelligent workshop environments, while also reducing operation time and path length. However, local path planning algorithms are highly dependent on real-time sensory data, making them prone to falling into local optima. Moreover, due to the lack of a holistic understanding of the global environment, they often fail to achieve globally optimal path planning.

Compared with local path planning algorithms, global path planning algorithms generate globally optimal paths based on comprehensive global map information. This approach avoids detours or redundancies caused by incomplete local information and effectively improves the accuracy and efficiency of path planning. Wang et al. [7] significantly reduced path search time and computational resource consumption in complex environments by combining Delaunay triangulation with the A* algorithm. Lu et al. [8] enhanced the performance of UAV three-dimensional path planning by improving the pheromone update rule in the ant colony algorithm and introducing a directional factor. Cao et al. [9] proposed a hierarchical multi-granularity three-dimensional UAV path planning method based on the A* algorithm, which improved search efficiency by optimizing the obstacle matrix and the open list of adjacent nodes. Allus et al. [10] developed an innovative multi-objective path planning sequencing algorithm that employs a “one distance-two angles” paradigm to optimize the visiting sequence of targets, thereby reducing computational complexity. Despite the significant advances in global path planning algorithms for path optimization, two core challenges remain. First, these algorithms are computationally intensive; when dealing with large-scale maps, the need to traverse a vast number of search points causes a surge in computation, greatly increasing planning time. Second, the smoothness of the planned paths is often inadequate. Current approaches typically generate paths by connecting discrete waypoints, neglecting the kinematic constraints of UAVs. This results in sharp-angle turns that fail to meet the smooth trajectory requirements of actual UAV operations in plant protection, thereby severely limiting the efficient control and maneuverability of such UAVs.

To address the problems of traditional path planning algorithms—namely high computational complexity, low search efficiency, and poor path smoothness due to non-compliance with kinematic constraints—this paper proposes a path planning method for plant protection UAVs based on the integration of dynamic weight functions and Bézier curves. First, an overall framework for the path planning algorithm is constructed based on the A* algorithm, and a weight function that dynamically adjusts along the path is introduced to improve the heuristic function of the A* algorithm, effectively reducing the number of search nodes and enhancing overall search efficiency. Then, second-order Bézier curves are integrated into the improved A* algorithm to reduce the number of turning points in the planning process and improve path smoothness. Finally, the effectiveness of the proposed algorithm is validated on Python and MATLAB platforms.

2. Algorithmic mechanism

2.1. Overall technical framework

This paper proposes a path planning method for plant protection UAVs based on the fusion of dynamic weight functions and Bézier curves. The overall technical framework is illustrated in Figure 1. First, parameter initialization is performed, including the start point, end point, as well as the open list and close list. Next, a dynamic weight coefficient w(n) is introduced to adjust the ratio between the actual cost and the estimated cost, thereby balancing the trade-off between search speed and path quality. The estimated cost H(N) is calculated to determine the corresponding value of the dynamic weight coefficient w(n), which is then used to modify the traditional A* algorithm. Finally, second-order Bézier curves are applied to smooth the turning points of the path generated by the improved A* algorithm, effectively enhancing the smoothness of the planned path.

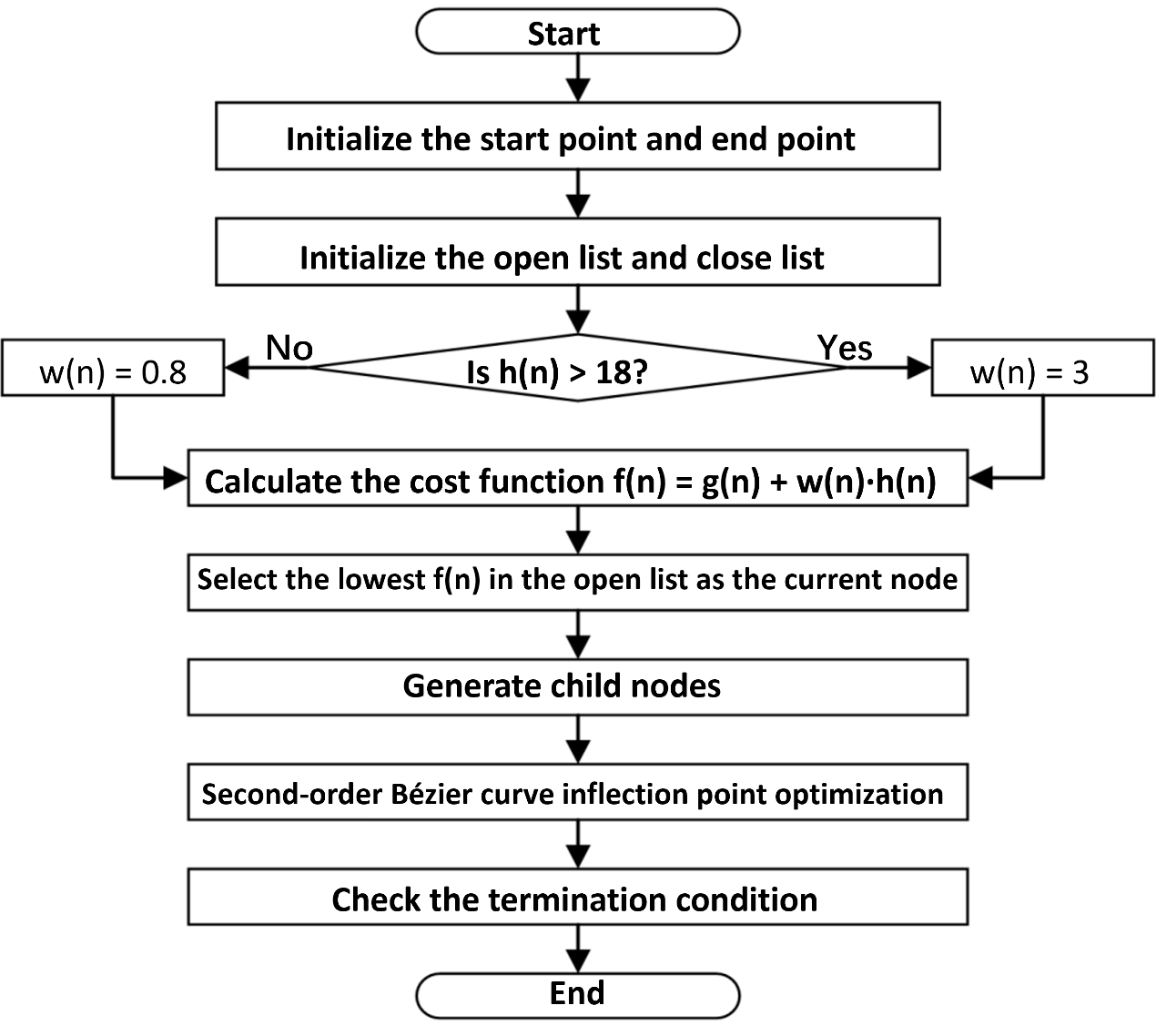
2.2. Principle of the A* algorithm

The A* algorithm is a heuristic search algorithm that improves search efficiency by introducing a heuristic function based on Dijkstra’s algorithm. First, the search area is divided into square grids, with the center of each grid cell defined as a node. Once a path is found, the agent moves from the center of one grid cell to the center of the next until reaching the destination. Next, two lists must be defined: an open list and a close list. The open list is used to store grid cells that are to be examined—these are potential candidates for the path, though not all of them will be included in the final path. Initially, the open list contains only one element, the starting point A. The close list stores grid cells that no longer need to be considered—these are cells that have been confirmed as part of the path. Then, a cost function needs to be defined.

$$$ \begin{array}{c}F\left(N\right)=G\left(N\right)+H\left(N\right)\end{array}$$$(1)

Where  $$ F\left(N\right)$$  is the cost function of node  $$ N$$ ,  $$ G\left(N\right)$$  is the movement cost from the start point to node  $$ N$$ , accumulated along the generated path to that grid, and  $$ H\left(N\right)$$  is the estimated cost from node  $$ N$$  to the designated target point, i.e., the endpoint.

$$$ \begin{array}{c}G\left(N\right)=\sum _{i=1}^{n}C\left(u_{i-1}{,u}_i\right)\end{array}$$$(2)

$$$ \begin{array}{c}H\left(N\right)=\{\begin{array}{c}\sqrt{{\left(x_g-x_n\right)}^2+{\left(y_g-y_n\right)}^2}\\ \left|x_g-x_n\right|+\left|y_g-y_n\right|\end{array}\end{array}$$$(3)

In the above formula,  $$ F\left(N\right)$$  is the cost function of node  $$ N$$ ,  $$ G\left(N\right)$$  is the movement cost from the starting point to node  $$ N$$  along the generated path to that grid cell, and  $$ H\left(N\right)$$  is the estimated cost from node  $$ N$$  to the specified target point, i.e., the endpoint;  $$ C$$  is the actual cost from the  $$ {(i-1)}^{th}$$  node to the  $$ i^{th}$$  node. The heuristic function  $$ H\left(N\right)$$  generally refers to a distance metric, which can be either the Euclidean distance or the Manhattan distance. These two distance calculation methods correspond to the straight-line distance between two points and the sum of the horizontal and vertical distances, respectively. In this experiment, the Euclidean distance method is adopted to calculate the heuristic function, namely  $$ \text{H}\left(\text{N}\right)\text{=}\sqrt{{\text{(}{\text{x}}_{\text{g}}\text{-}{\text{x}}_{\text{n}}\text{)}}^{\text{2}}\text{+}{\text{(}{\text{y}}_{\text{g}}\text{-}{\text{y}}_{\text{n}}\text{)}}^{\text{2}}}$$ , where  $$ \left(x_n,y_{n,}\right)$$  are the coordinates of node  $$ N$$ , and  $$ \left(x_g,y_g\right)$$  are the coordinates of the target point. The path generated by the A* algorithm output consists of multiple discrete points stored in the close list. Let the starting point be  $$ P_0$$  and the target point be  $$ P_n$$ ; then the generated path can be represented as

$$$ \begin{array}{c}route =\left(P_0,P_1,P_2,\dots ,P_n\right)\end{array}$$$(4)

The total cost of the path is

$$$ \begin{array}{c}distance=\sum _{i=1}^{n}d\left(P_{i-1},P_i\right)\end{array}$$$(5)

Where  $$ d\left(P_{i-1,}{P}_i\right)$$  is the distance between the previous node and the current node.

2.3. Improvement of the heuristic function

In path planning algorithms, the A* algorithm is widely used because it balances the actual path cost and the heuristic estimate. However, in the traditional A* algorithm, the cost function F $$ F\left(N\right)=G\left(N\right)+H\left(N\right)$$  assigns equal weight to the actual cost  $$ G\left(N\right)$$  and the estimated cost  $$ H\left(N\right)$$ , with a fixed ratio of 1:1. This often leads to low search efficiency. To address this, this paper proposes an improved method based on the dynamic adjustment of the weight coefficient. By introducing a dynamic weight coefficient w(n) to regulate the ratio between the actual cost and the estimated cost, the performance of the A* algorithm is optimized [11]. The cost function is modified as follows

$$$ \begin{array}{c}F\left(N\right)=G\left(N\right)+w\left(n\right)*H\left(N\right)\end{array}$$$(6)

The value of the weight coefficient w(n) is adjusted based on the estimated cost H(N) of the current node. The dynamic weighting strategy proposed in this paper essentially balances the trade-off between search speed and path quality during the pathfinding process. When the weight coefficient w(n) is relatively large, the algorithm behaves more aggressively, quickly covering a larger search space, which is suitable for the early stages of the search. Conversely, as the algorithm approaches the target, reducing w(n) makes the search more cautious, prioritizing paths with lower costs. This flexible weight adjustment mechanism effectively reduces the number of search nodes and improves overall search efficiency. The specific adjustment strategy is as follows

1) Rapid Search Phase: When  $$ H\left(N\right)>18$$ , set  $$ w\left(n\right)=3$$ . At this stage, the A* algorithm is in the initial phase of the search and far from the target point. By increasing the weight of the estimated cost, the algorithm tends to expand quickly toward the target area, thereby improving search speed.

2) Fine Search Phase: When  $$ H\left(N\right)<18$$ , adjust the weight coefficient to  $$ w\left(n\right)=0.8$$ . At this point, the algorithm is close to the target area and begins to emphasize path optimality. Reducing the weight of the estimated cost causes the algorithm to consider the actual path cost more, thus optimizing the search results.

2.4. Bézier curve smoothing

Bézier curves, developed from Bernstein polynomials, feature a simple control structure that allows for smooth processing of curves according to corresponding strategies. Therefore, this paper employs second-order Bézier curves to smooth the turning points of the path generated by the improved A* algorithm, effectively enhancing the smoothness of the flight trajectory. The parametric equation for a point on a Bézier curve [12] is:

$$$ \begin{array}{c}P\left(t\right)=\sum _{i=1}^n{P}_i{B}_{i,n\left(t\right)} \end{array}$$$(7)

Where P(t) is the motion control point on the Bézier curve;  $$ P_i$$  is the position of the  $$ i^{th}$$  point;  $$ B_i$$  is the  $$ n^{th}$$ -order Bernstein polynomial; and  $$ n$$  is the internal control parameter of the curve. The Bernstein polynomial  $$ B_{i,n\left(t\right)}$$  satisfies:

$$$ \begin{array}{c}{B}_{i,n\left(t\right)}=c_n^i{t}^i{\left(1-t\right)}^{n-1}=\frac{n!}{\left(n-i\right)!i!}{t}^i{\left(1-t\right)}^{n-i}\end{array}$$$(8)

$$$ i=\mathrm{0,1},\cdots ,n$$$

Where  $$ c_m^i$$  is the binomial coefficient for the quadratic term, and  $$ m$$  is the order of the Bézier curve. Traditional path planning methods connect given control points sequentially to form a polygon, whereas the Bézier curve algorithm infinitely and smoothly approximates this polygon. The schematic illustration of this principle is shown in Figure 2.

Define  $$ P_0$$ ,  $$ P_1$$  and  $$ P_2$$  as three control points, where the parameter  $$ t$$  takes values in the range [0,1], that is:

$$$ \begin{array}{c}{P}_{\mathrm{1,0}}\left(t\right)=\left(1-t\right)P_0+t{P}_1\end{array}$$$(9)

$$$ \begin{array}{c}{P}_{\mathrm{1,2}}\left(t\right)=\left(1-t\right)P_1+t{P}_2\end{array}$$$(10)

 $$ P_{\mathrm{1,0}}\left(t\right)$$  and  $$ P_{\mathrm{1,2}}\left(t\right)$$  are the first-order Bézier points on the line segments  $$ P_1{P}_0$$  and  $$ P_1{P}_2$$ , respectively. The expression for the second-order Bézier curve is:

$$$ \begin{array}{c}P\left(t\right)={\left(1-t\right)}^2{P}_0+2t\left(t-1\right)P_1+t^2{P}_2\end{array}$$$(11)

In the formula,  $$ P_0$$  is the starting point of the second-order Bézier curve,  $$ P_1$$  is the control point, and  $$ P_2$$  is the endpoint of the second-order Bézier curve.

3. Experimental validation

3.1. Algorithm performance comparison experiment

The experiments were conducted in the Python 3.13 environment. The initial map was set to 70 × 70 units, with a grid size of 2.0 units. To account for the UAV’s size, the robot radius was set to 1.0. The traditional A* algorithm, the A* algorithm integrated only with the dynamic weight function, the A* algorithm integrated only with the Bézier curve method, and the A* algorithm integrating both the Bézier curve method and dynamic weight function were run on the map. The same start and end points were used under identical map sizes and obstacle sparsity to observe the effects of different algorithm improvements on path planning. The start point was set at (−5, −5) and the end point at (55, 55). The simulation results are shown in Figure 3, and the performance comparison is presented in Table 1:

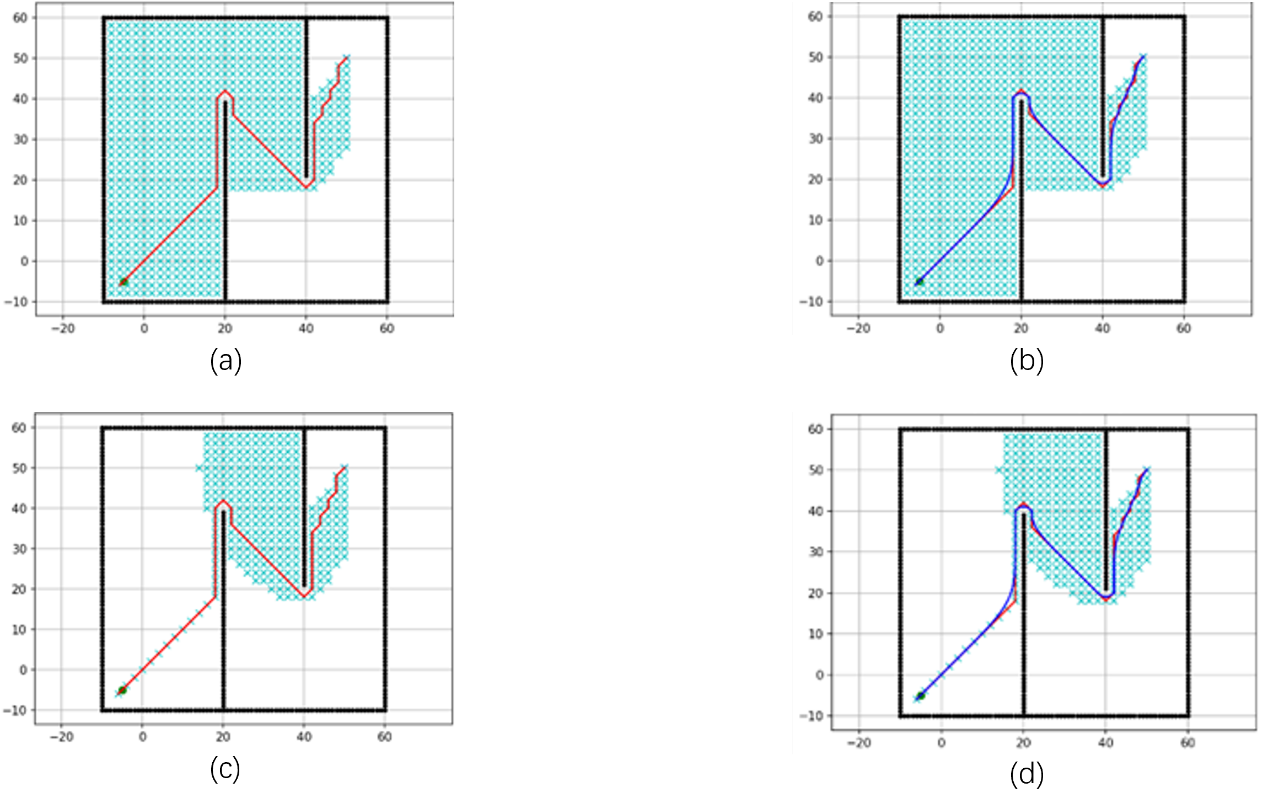
Where (a) represents the path generated by the traditional A* algorithm, (b) the path generated by the A* algorithm integrated only with the dynamic weight function, (c) the path generated by the A* algorithm integrated only with the Bézier curve method, and (d) the path generated by the A* algorithm integrating both the dynamic weight function and Bézier curve. By statistically analyzing the data from the experimental paths.

As shown in Figure 3 and Table 1, the traditional A* algorithm traverses the greatest number of search nodes (represented by blue crosses in the figure), totaling 482 nodes, and has the longest search time at 0.85 seconds. In contrast, the A* algorithm integrated with the dynamic weight function reduces the number of search nodes by 38.8% compared to the traditional A* algorithm, significantly improving search efficiency. The path planned by the traditional A* algorithm contains 18 turns, whereas after integrating the Bézier curve method, the number of turns decreases to 5, a reduction of 72.2%, markedly enhancing path smoothness. The proposed method, which fuses both the dynamic weight function and Bézier curve with the A* algorithm, reduces the number of search nodes from 482 to 295—a 38.8% decrease—and decreases the number of turns from 18 to 8, a 55.6% reduction, compared to the traditional A* algorithm. These results demonstrate that the improved path planning algorithm proposed in this paper significantly enhances both search efficiency and path smoothness.

3.2. Analysis of the impact of dynamic weight

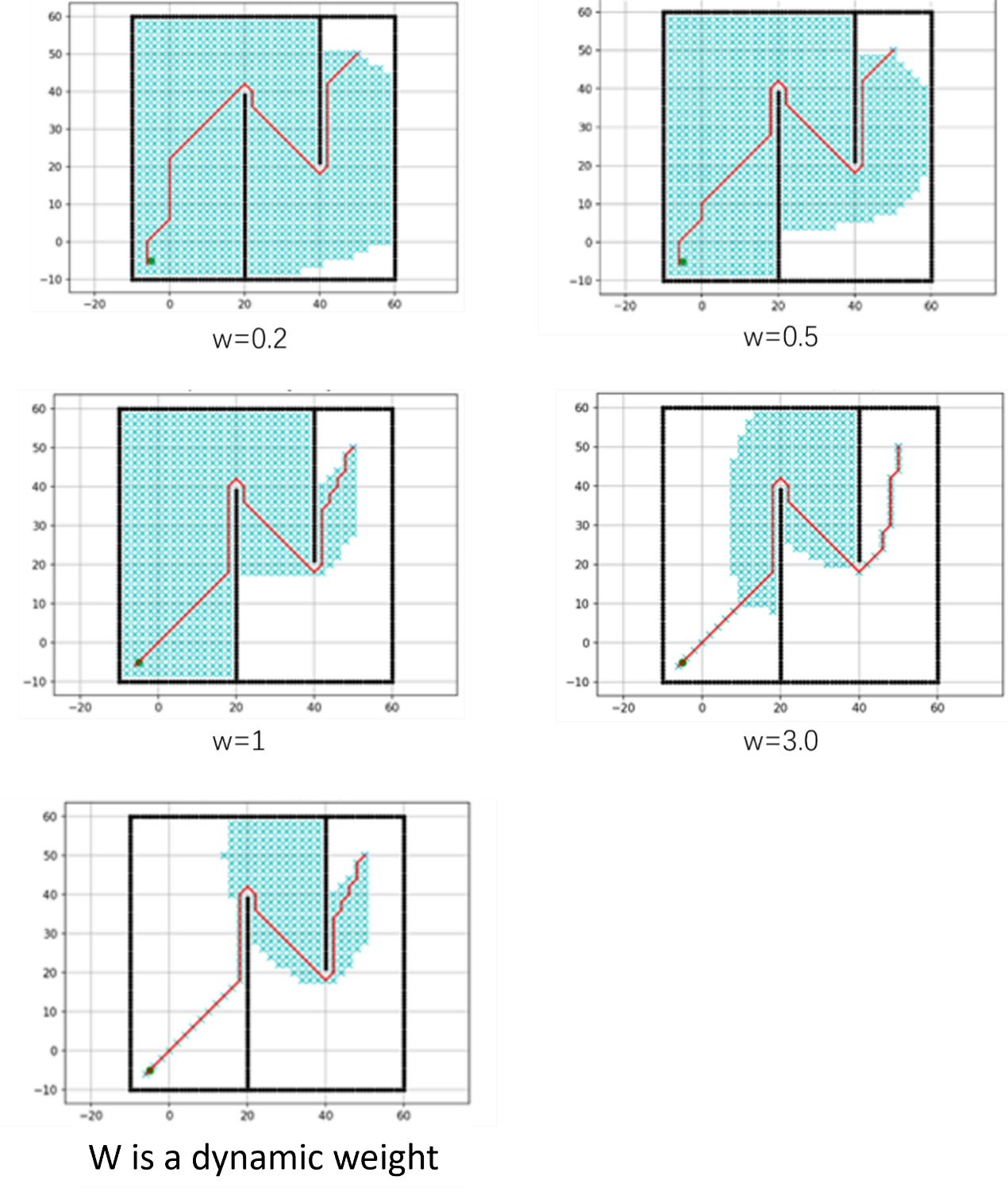
To analyze the effect of different values of the dynamic weight function on path planning performance, the heuristic function’s weight coefficient was set to 0.2, 0.5, 1.0, 3.0, and dynamically adjusted weight, respectively. The map size and the start and end points were kept the same as in the previous experiment. The comparative results are shown in Figure 4, and the performance comparison of different weighting schemes is presented in Table 2.

Path quality was evaluated using a comprehensive 10-point scoring system encompassing four core dimensions: Basic Efficiency (3 points): Focuses on path directness, measured by the deviation of the path length from the theoretical shortest path and the redundancy ratio between the total path length and the straight-line distance from start to end. Smoothness (2.5 points): Emphasizes motion stability, assessed based on whether the path’s maximum curvature complies with the robot’s tolerance and the frequency of turns (direction changes ≥ 15°). Safety (3 points): Centers on collision avoidance, primarily examining the minimum safe distance between the path and obstacles relative to the robot’s radius; in dynamic environments, additional evaluation considers the spatiotemporal overlap with moving obstacle trajectories. Feasibility (1 point): Verifies whether the path aligns with the robot’s motion capabilities, including whether the distances between adjacent points and turning angles fall within mechanical constraints. The total score is the sum of the four dimensions, with a maximum of 10 points. Scores between 9 and 10 are rated excellent, 7 to 8 good, 5 to 6 acceptable, and below 5 unacceptable. This system comprehensively reflects the overall performance of the path in terms of efficiency, smoothness, safety, and executability.

Analysis of Figure 4 and Table 3 shows that the path length, search time, and number of search nodes in path planning all exhibit a negative correlation with the weight coefficient. Specifically, as the weight coefficient increases, the path length gradually decreases, search time shortens, and the number of search nodes reduces. For example, when the weight coefficient w=3.0, the path length is minimized (128.4 m), the search time is the shortest (0.65 s), and the number of search nodes is the lowest (280). Compared to the traditional A* algorithm with w=1.0, this represents a 5.4% reduction in path length, a 49.2% decrease in search time, and a 65.9% reduction in search nodes. Unfortunately, as the weight coefficient increases, the overall path quality score declines from 8.5 to 7.5, indicating a significant drop in quality.

For the dynamic weight coefficient, the searched path length is 132.5 m, the search time is 0.78 s, and the number of search nodes is 320. Compared to the traditional A* algorithm with w=1.0, this represents a 2.3% reduction in path length, a 39.1% decrease in search time, and a 28.9% decrease in search nodes. Although the dynamic weight coefficient results in slightly higher values in path length, search time, and number of search nodes compared to the case with w=3.0, the path quality score achieved is 9.1—significantly higher than the 7.5 score at w=3.0 and only 0.1 lower than that at w=1.0. This demonstrates that the dynamic weight coefficient substantially improves the quality of path planning.

3.3. Analysis of Bézier curve smoothing effect

To analyze the improvement in path smoothness achieved by the Bézier curve algorithm, this paper constructs a three-dimensional spatial environment featuring undulating terrain that better reflects the topographical changes encountered during UAV flight. The start point is set at (11, 11, 1.5), and the end point at (1, 1, 0.6). As shown in Figure 5, the blue path represents the route planned by the traditional A* algorithm, while the red path corresponds to the path planned by the A* algorithm integrated with the Bézier curve method. Using path length, number of path nodes, and number of turning points as evaluation metrics, the performance comparison results are presented in Table 3.

As shown in Figure 5 and Table 3, the proposed A* optimization algorithm incorporating Bézier curve smoothing can be effectively implemented in a three-dimensional environment. Additionally, for the same start and end points, the path length planned by the A* algorithm with Bézier curve integration decreased from 152.34 m to 148.56 m, a reduction of 10.7%. The number of nodes decreased from 28 to 25. Most notably, the number of turning points was reduced from 12 to 5, a 58.3% decrease, indicating a significant improvement in trajectory smoothness.

4. Conclusion

This paper addresses the issues of high computational complexity, low search efficiency, and poor path smoothness caused by traditional path planning algorithms that do not comply with kinematic constraints. A path planning method for plant protection UAVs based on the fusion of dynamic weight functions and Bézier curves is proposed, and the effectiveness of the algorithm is verified on Python and MATLAB platforms. The main conclusions are as follows:

1) By introducing a dynamically adjusted weight function into the heuristic function of the A* algorithm, the number of search nodes can be effectively reduced, thereby improving overall search efficiency. Integrating the second-order Bézier curve with the improved A* algorithm reduces the number of turning points during path planning, significantly enhancing path smoothness.

2) After fusing the dynamic weight function and Bézier curve algorithms with the A* algorithm, compared to the traditional A* algorithm, the number of search nodes decreased from 482 to 295, a reduction of 38.8%; the number of path turns reduced from 18 to 8, a decrease of 55.6%.

3) Compared with the search performance at a weight coefficient of  $$ w$$ =3.0, although the dynamic weight coefficient results in slight increases in path length, search time, and number of search nodes, the path quality score achieved using the dynamic weight coefficient is 9.1—significantly higher than the 7.5 score at  $$ w$$ =3.0 and only 0.1 lower than that at  $$ w$$ =1.0. Thus, the path planning quality is significantly improved by adopting the dynamic weight coefficient.