1. Introduction

Amid the rapid advancement of artificial intelligence, Few-Shot Learning (FSL) has emerged as a key approach to mitigating the dependence of supervised learning on large-scale labeled data, especially in data-scarce scenarios such as medical diagnosis, remote sensing, and edge computing. Meta-learning excels in FSL by leveraging shared knowledge across tasks for rapid adaptation, while Multi-Armed Bandit (MAB) algorithms dynamically balance exploration and exploitation in uncertain environments, showing flexibility in task scheduling and sample selection. Although both have achieved significant progress independently, the integration of the two in few-shot learning remains underexplored in terms of improving training efficiency, generalization, and task selection strategies, highlighting the need for a unified mechanism to enhance learning performance under complex and dynamic conditions. This study aims to construct an intelligent learning framework that integrates task scheduling and rapid adaptation, promoting the practical application of FSL in complex real-world scenarios. To this end, it focuses on the synergistic mechanism and application advantages of meta-learning and MAB algorithms in FSL, exploring how to effectively integrate the two to boost training efficiency and generalization in data-scarce and non-stationary environments. By combining literature review and analysis of representative cases, this study summarizes key strategies and implementation pathways, aiming to provide theoretical foundations and practical guidance for model training in resource-constrained environments.

2. Overview of meta-learning and Multi-Armed Bandit algorithms

2.1. Foundations and key methods of meta-learning

To overcome the reliance of deep learning on large labeled datasets and fixed tasks, meta-learning introduces a paradigm for efficient generalization across diverse tasks with minimal supervision. In contrast to traditional models that rely heavily on large-scale annotations, meta-learning leverages multi-task training to acquire knowledge that generalizes across tasks. This adaptability has shown considerable promise in fields such as image recognition, natural language processing, and medical diagnosis [1,2]. Formally, meta-learning assumes tasks are sampled from a distribution  $$ \mathrm{p}\left(\mathcal{T}\right)$$ , with the objective of learning an initialization  $$ \theta $$  that enables rapid adaptation through gradient-based updates.

$$ {\theta }_i^{\mathrm{\text{'}}}=\theta -\alpha {\nabla }_{\theta }{\mathcal{ℒ}}_{{\mathcal{T}}_i}\left(f_{\theta },{\mathcal{D}}_i^{\mathrm{t}\mathrm{r}}\right)$$(1)

where  $$ \alpha $$  denotes the learning rate, and  $$ {\mathcal{ℒ}}_{{\mathcal{T}}_i}$$  is the loss function for task  $$ {\mathcal{T}}_i$$ . The meta-learning objective then minimizes the post-adaptation loss across tasks.

$$ \underset{\theta }{\mathrm{m}\mathrm{i}\mathrm{n}}{\mathbb{E}}_{{\mathcal{T}}_i\sim p\left(\mathcal{T}\right)}\left[{\mathcal{C}}_{{\mathcal{T}}_i}\left(f_{{\theta }_i^{\mathrm{\text{'}}}},{\mathcal{D}}_i^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}\right)\right]$$(2)

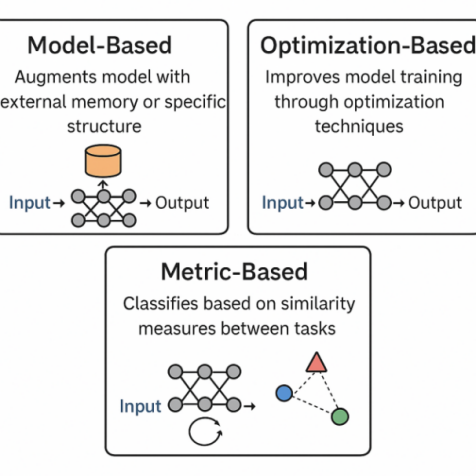
At present, meta-learning methods are generally divided into three categories, as shown in Figure 1, each reflecting a distinct mechanism for enabling rapid adaptation. Model-based methods boost a model’s capacity to store and retrieve task-relevant information by introducing external memory structures (e.g., MANN) or attention mechanisms (e.g., SNAIL), which makes them well-suited for environments with frequent task switching. In contrast, optimization-based methods learn parameter initialization or update rules that enable fast adaptation with few gradient steps. For example, Model-Agnostic Meta-Learning (MAML) achieves strong adaptability and transfer performance across tasks [3]. Metric-based methods, by comparison, construct a similarity space for comparing samples, allowing efficient classification of new instances. Approaches like Prototypical Networks and Matching Networks are particularly effective in few-shot scenarios with clearly defined classes [2]. Despite its effectiveness in few-shot learning, meta-learning still struggles with generalization and task distribution shifts. Nevertheless, challenges remain in generalization and task distribution shifts, suggesting room for further refinement and integration with other learning paradigms.

2.2. Multi-Armed Bandit algorithms and their application foundations

The MAB problem seeks to maximize cumulative rewards by repeatedly selecting from multiple options while balancing exploration of uncertain choices and exploitation of the best-known one under limited feedback. In order to manage this trade-off, several strategies have been proposed. For instance, the ε-greedy strategy performs random exploration with a fixed probability ε, selecting the highest-reward option otherwise, and is favored for its simplicity and efficiency. The UCB algorithm leverages confidence bounds to guide selection, enabling active exploration of promising options while balancing theoretical guarantees and empirical performance. Exponential-weighting methods such as EXP3 are designed for non-stationary environments, offering strong adaptability in highly uncertain settings with sparse rewards [4]. In recent years, MAB algorithms have attracted growing interest in federated learning, primarily for dynamic client selection to enhance training efficiency and communication reliability. For example, applying the UCB strategy to autonomously select clients with stable computation and representative data can reduce communication overhead and training latency while maintaining model accuracy [5,6]. In federated learning, UCB-based client selection achieves adaptive scheduling by evaluating clients across multiple dimensions:

$$ i_t=\mathrm{a}\mathrm{r}\mathrm{g}\underset{i\in {\mathcal{C}}_t}{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\underset{\text{model quality}}{\underbrace{\mathrm{Q}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\left({\mathbf{w}}_i,{\mathcal{D}}_i\right)}}+\underset{\text{system efficiency}}{\underbrace{\text{Efficiency}\left({\mathbf{c}}_i\right)}}+\beta \cdot \underset{\text{adaptive tuning}}{\underbrace{\text{Exploration}\left(n_i\right)}}\right)$$(3)

where  $$ c_i$$  captures the computational and communication characteristics of clients.

Based on Bayesian optimization, the method encodes device stability and data representativeness as confidence bounds, while using meta-learned priors to adjust exploration intensity. This hybrid mechanism preserves global model convergence and significantly reduces resource consumption during synchronous updates, making it well-suited for distributed learning environments with heterogeneous devices and unstable networks.

Moreover, by integrating MAB with meta-learning, the approach leverages MAB’s selective filtering to optimize task or data selection during meta-training. This accelerates model convergence under few-shot conditions and improves generalization. The effectiveness of this fusion lies in their theoretical complementarity: MAB ensures optimal task selection via confidence bounds, while meta-learning enables rapid adaptation across tasks through gradient-based updates. The strength of this fusion lies in the theoretical complementarity between MAB and meta-learning. MAB ensures optimal task selection via confidence-bound mechanisms, while meta-learning enables cross-task generalization via rapid gradient-based adaptation. Their synergy is formalized over the probability space  $$ (T,\Sigma ,P)$$ , where  $$ T$$  denotes the task set,  $$ \Sigma $$  the σ-algebra, and  $$ P$$  the task distribution.

$$ \mathbb{E}\left[\sum _{t=1}^T{\mathcal{ℒ}}_{{\tau }_t}\left({\theta }_t\right)\right]\le \psi \left(T\right)+\underset{\text{MAB optimality}}{\underbrace{\underset{\theta \in \Theta }{\mathrm{i}\mathrm{n}\mathrm{f}}\parallel {\nabla }_{\theta }{\mathcal{ℒ}}_{\tau }\left(\theta \right)\parallel \le \kappa ϵ}}$$(4)

where $$ \psi \left(T\right)=O\left(\sqrt{Tlog\left|T\right|}\right)$$  is the MAB regret function and  $$ \kappa $$  is the smoothing coefficient of task loss. The theoretical framework explicitly explains the robustness advantage of the strategy in complex distributional scenarios [5,7]. Hence, MAB algorithms, originally applied in reinforcement learning and recommendation systems, have proven highly adaptable to intelligent scheduling and few-shot optimization. Incorporating contextual modeling and Bayesian inference further improves their stability and generalization in dynamic environments, thus offering efficient decision-making support for multi-task systems such as federated learning.

3. Synergistic mechanisms and applications of meta-learning and Multi-Armed Bandits

3.1. Framework design and synergy principles

The strengths of meta-learning and MAB algorithms align well to enhance performance in few-shot learning. Specifically, meta-learning enables rapid adaptation by learning shared representations across tasks, allowing models to generalize from limited data. In parallel, MAB algorithms enhance data efficiency by adapting selection strategies to feedback, reducing trial-and-error costs. To enable efficient training under limited data and adapt to shifting task distributions, meta-learning and MAB can be integrated into a unified framework. Within this framework, MAB plays a critical role by balancing exploration and exploitation, with its selection mechanism formalized as:

$$ {\mathrm{a}}_{\mathrm{t}}=\mathrm{a}\mathrm{r}\mathrm{g}{m}_{\mathrm{a}\in \mathrm{A}}({\widehat{\mu }}_a+\sqrt{\frac{2\mathrm{l}\mathrm{n}\mathrm{t}}{{\mathrm{n}}_{\mathrm{a}}}})$$(5)

where  $$ {\widehat{\mu }}_a$$  denotes the return estimate for action a and  $$ {\mathrm{n}}_{\mathrm{a}}$$  is the number of historical choices. With a regret upper bound of  $$ \mathrm{O}(\surd \mathrm{T}\mathrm{ }\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{ }\mathrm{K})$$ , the algorithm minimizes trial-and-error overhead. When combined with meta-learning, the two complement each other’s strengths. Meta-learning extracts a shared representation  $$ \mathrm{\varphi }\left(\mathrm{T}\right)$$  through cross-task modeling, providing task feature embeddings that help MAB adjust its selection strategy to dynamic task distributions. This synergistic mechanism can be formalized as follows.

$$ \mathrm{\pi }\left(\mathrm{a}|\mathrm{T}\right)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{U}\mathrm{C}\mathrm{B}\left(\mathrm{\varphi }\left(\mathrm{T}\right)\right)\right)$$(6)

where the meta-learning parameter  $$ {\theta }_{meta}$$  accelerates the initialization of MAB. Experiments show that in scenarios like federated learning, the joint approach significantly reduces the number of communication rounds while maintaining stable performance improvement in non-smooth task flows, providing both efficient and robust solutions for few-shot learning. The integration of MAB and meta-learning builds a closed-loop adaptive mechanism that enhances both task selection and model generalization. MAB guides the scheduling process by estimating task or data value from historical feedback, prioritizing informative or representative inputs to suppress noise and improve training efficiency. By leveraging shared representations and updating with MAB-filtered inputs, meta-learning improves selection accuracy and speeds up convergence in few-shot learning. The mechanism generalizes across multiple scenarios. In federated learning, it reduces communication rounds by prioritizing high-utility clients and adapting to non-IID data. In semi-supervised learning, it enhances pseudo-label quality via confident sample selection. In data selection or augmentation, it filters redundancy and maximizes utility per sample. By combining global scheduling with local adaptation, the approach balances exploration and exploitation under limited supervision, offering a robust and efficient solution for complex learning environments [1,8].

3.2. Empirical applications and experimental validation

The combination of meta-learning and MAB demonstrates strong adaptability in few-shot scenarios, boosting training efficiency and generalization under data scarcity, task heterogeneity, and resource constraints. In federated image classification, large gaps in computing resources and uneven data distribution among clients often lead to inefficient training and reduced model performance when using traditional unified scheduling.

To address data scarcity, task diversity, and resource limits, MAB algorithms are combined with meta-learning in intelligent optimization schemes. For instance, the MAB module scores clients by accuracy and latency, selecting those with better data and faster response for training. This strategy achieves a theoretical regret upper bound of  $$ \mathrm{O}\left(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{ }\mathrm{T}\right)$$ , greatly outperforming random scheduling. Meanwhile, the meta-learning module initializes parameters with  $$ {\theta }_{meta}$$ , enabling selected clients to adapt with only 3-5 rounds of local updates, thereby improving overall training efficiency. This mechanism achieves 83.5% test accuracy on the CIFAR-10 non-IID dataset, 15% higher than the baseline. It reduces communication rounds by 38%, lowers energy consumption by 40%, and cuts the dropout rate from 25% to 9%. It also performs well in medical imaging, improving F1-score for rare disease detection by 20%, and in smart manufacturing, reducing model adaptation time from one day to one hour [5]. These results provide an efficient and effective solution for heterogeneous federated learning. In remote sensing image analysis, to address scale variation and uneven spatial distribution, researchers propose a MAB-based dynamic region selection strategy that trains only on regions with confidence scores above 0.9. This reduces noise by 35% and improves object detection mAP from 72.3% to 82.5%. Meanwhile, meta-learning enables fast adaptation under few-shot conditions by leveraging cross-task shared representations ( $$ \mathrm{\varphi }\ast $$ ), boosting cross-region land cover recognition mAP from 54.2% to 68.7%. For ECG classification tasks, the mechanism alleviates class imbalance via dynamic sample weighting (e.g.,  $$ \text{w(x)=}\text{1/(1}\text{+}{e}^{-\alpha (p-\tau )})$$ ), raising the F1-score for rare diseases from 0.41 to 0.66. With meta-pretraining on 12 public ECG datasets, it achieves 98.2% accuracy for common arrhythmias and increases recall for rare conditions to 89.4%. Training efficiency more than doubled while loss variance dropped by 60% [2,9]. In robotic manipulation, meta-learning enables fast transfer of grasping strategies, while MAB optimizes action paths to improve task efficiency. For industrial equipment diagnostics, the mechanism reacts to frequent state changes in real time (latency <50ms) and maintains 94.3% fault classification accuracy even in non-stationary environments. Through cross-device pretraining, the meta-learning module enables adaptation to new devices with just 3-5 updates by learning device-agnostic representations ( $$ {\theta }_{meta}$$ ) . Meanwhile, the MAB algorithm optimizes diagnostic paths, lowering the false alarm rate from 12% to 4% and reducing diagnosis time from 2.1 s to 0.3 s. Field tests show the system maintains 87% accuracy on unseen device types (vs. 68% for baseline methods) and runs stably on edge devices like Raspberry Pi (200MB RAM) [8].

3.3. Existing challenges and optimization approaches

Although the synergistic mechanisms of meta-learning and MAB algorithms have shown promising results across several tasks, key bottlenecks remain in generalization ability, strategy stability, and adaptation to complex environments. Specifically, meta-learning often overfits to local task features when faced with drastic shifts in task distribution or cross-domain transfers, hindering its ability to consistently capture high-level shared structures and reducing adaptability. This issue is especially pronounced with large inter-task variations, where the meta-model’s initialization parameters may fail to generalize effectively, slowing convergence. In addition, the deficiency of a reliable task similarity assessment hinders clear guidance for task scheduling and updates, limiting the ability to handle heterogeneous tasks. Besides, the MAB strategy faces sparse feedback and noise during early exploration. With many candidate tasks or clients, it demands extensive trial and error, leading to slow convergence, inefficient updates, and potential local optima. Traditional MAB methods face challenges in high-dimensional contexts, hampering their ability to model nonlinear task-reward relationships and undermines performance in complex scheduling.

In response to the above challenges, various optimization strategies have been developed. For the meta-learning part, incorporating a similarity discrimination module based on task meta-features like a task embedding network or attention mechanism effectively improves task matching accuracy and initialization generalization. Meanwhile, combining meta-regularization with meta-expansion greatly enhances the model’s robustness to task perturbations and reduces the risk of overfitting to local features [2]. These methods employ a unified optimization objective and a two-level automatic parameter tuning mechanism, achieving theoretically strict control over generalization error. For the MAB strategy, traditional ε-greedy and UCB approaches have been extended into context-aware or Bayesian inference frameworks. By leveraging a task feature encoder to integrate historical information, these frameworks improve the stability and noise robustness of task selection [4,5]. Experiments demonstrate that this strategy reduces selection variance by approximately 40% in federated learning scenarios. Moreover, incorporating sparse reward reconstruction techniques such as inverse reinforcement learning or fuzzy reward modeling effectively alleviates sparse feedback during exploration and accelerates strategy optimization. At present, collaborative mechanisms are shifting toward end-to-end optimization. Typical methods include embedding MAB into the outer loop of meta-learning as a scheduling method, designing unified reward functions for gradient-level collaboration, and constructing closed-loop optimization systems for strategy parameters. Future work should target heterogeneous task modeling, context awareness, and cross-domain transfer to improve stability and efficiency in dynamic, data-scarce environments.

4. Future potential and broader applications

Few-shot learning demonstrates significant advantages in scenarios characterized by limited data availability and high labeling costs, increasingly becoming a fundamental capability for deploying intelligent systems. As the integration of meta-learning and MAB algorithms continues to advance, this approach holds broad potential for rapid model adaptation and dynamic resource optimization.

In medical electrocardiogram (ECG) signal classification tasks, marked physiological differences among individuals, scarcity of pathological data, and the complexity of accurate annotation present significant challenges for traditional deep learning models to generalize effectively. Incorporating meta-learning mechanisms enables models to extract features across individuals and quickly adapt to new tasks with few samples, markedly enhancing classification accuracy and transferability. In addition, MAB strategies optimize the selection and allocation of training samples, allowing models to concentrate on diagnostically important segments and effectively mitigate overfitting risk. In the field of radar target recognition, key challenges include diverse target types, imbalanced data, and environmental interference. In response, embedding meta-learning within a multi-task framework combined with memory-augmented modules equips models with the ability to continually learn new categories while maintaining stability of previously acquired knowledge. The guidance provided by MAB in target scheduling and sample selection enhances the model’s adaptability and robustness across diverse scenarios, demonstrating particularly strong performance under long-range and low signal-to-noise ratio conditions. In the coming years, the synergy between meta-learning and MAB is poised to unlock considerable potential across diverse avenues. In particular, the introduction of contextual memory networks and meta-representation modeling may enable long-term dependency modeling across tasks and facilitate rapid knowledge transfer. Besides, dynamic weight allocation and multi-scale representation techniques can boost the model’s ability to integrate heterogeneous tasks and multi-source data. Moreover, in environments characterized by frequent task switching or rapidly changing target states, combining reinforcement learning with policy compression methods can accelerate convergence and improve deployment efficiency. This approach has already shown strong scalability in dynamic and complex environments such as remote sensing image recognition, intelligent manufacturing, and robotic control, thus providing a versatile framework for developing intelligent systems with robust generalization capabilities. Heterogeneous data fusion, robustness evaluation, and task-adaptive scheduling should receive increased focus in future research to enable true “small-data intelligence” and speed up the practical deployment of intelligent algorithms [1,7]

5. Conclusions

This paper provides a systematic review of the synergistic mechanisms, application performance and technical challenges of meta-learning and MAB algorithms in few-shot learning. It is shown that the combination strategy can effectively improve the model’s learning efficiency and adaptive ability in data-scarce scenarios, which provides new ideas for solving the generalization bottleneck and resource scheduling problems in real tasks. This study addresses the key question of improving few-shot model performance and provides theoretical support and methodological references for building an intelligent, adaptive learning system. As a next step, future research should further investigate cross-domain generalization and adaptive strategy updating to advance the development of few-shot intelligent systems.