1. Introduction

1.1. Brief Introduction to Gravitational Wave Astronomy

Ever since the establishment of general relativity and the prediction of gravitational waves (GW) that propagate at the speed of light, the community has been expecting the detection of GW for nearly one century. The seminal discovery of orbital period evolution in a pulsar binary system confirmed the (indirect) existence of GW for the first time [1], but only in 2016 we finally have the direct detection of GW signal. The GW150914 event, occurred on September 14, 2015, involved the merger of two stellar-mass black holes (BHs) with estimated masses of 29 M⊙ and 36 M⊙[2]. Since then, nearly 100 GW signals from compact binary coalescences have been successfully detected. These GW signals are primarily produced by binary BHs (BBHs), and two by binary BH-NS (neutron star), and one by binary NS. The fruitful and steady detections of GW events have made GW astronomy a reality. With detector sensitivity improving further from LIGO-VIRGO, and new GW facilities in near future (e.g., KAGRA, Taiji), more and more GW events will have tighter location constraints.

GW further strengthens the era of multi-messenger astronomy. It can coordinate the electromagnetic wave, neutrino and cosmic rays.

The detection of GW is of crucial importance in many aspects. Below we highlight two of them. First, it can test the general relativity in the relativistic and strong-gravity regime. With BBH and BNS GW signals, we can deepen our understanding in gravity itself, and probe possible deviations to general relativity. Second, it can be used to investigate cosmology, e.g., the Hubble constant. One unique feature of GW is that it follows R-1 law during propagation (for comparison, others, e.g. radiation and cosmic ray flux, all follow R-2 law). Together with the absolute strength predicted from the GW model, we can have an independent measurement of distance. Combined with redshift measurement in optical wavebands, we can calibrate the evolution of our Universe.

1.2. Urge for New Techniques in Data Analysis

The successful detection of GW signals has provided valuable experimental data for GW astronomy and initiated a wave of GW research.

Currently, the matched filtering method is primarily used by both LIGO and Virgo to detect gravitational wave signals. This technique involves building a theoretical waveform template bank to match the monitored data and capturing trigger signals as candidates for further verification. Although matched filtering has been vital in the processing of gravitational wave signal detection, it has limitations, including a full search requirement in the template bank, which limits the data processing speed. Additionally, with an expanding parameter space, the search space of matched filtering increases, leading to a reduction in processing speed. The matched filtering technique is still being used in the current third observation run, which began in April 2019. With the expected increase in data from future observation runs, it is necessary to accelerate parameter estimation algorithms to keep up with the data processing demands.

To resolve these issues, machine learning algorithms, like deep learning, are powerful tools to use. Recent advancements in machine learning have led to the development of deep learning algorithms that have achieved remarkable success in various fields, including image classification, natural language processing, and speech recognition. In particular, deep learning algorithms, such as convolutional neural networks (CNNs), have shown significant improvements in model accuracy and complexity, particularly in classification tasks [3]. Additionally, the offline training process of deep learning algorithms reduces the amount of computation required during online data analysis, which is ideal for real-time detection. Therefore, machine learning algorithms, especially deep learning, can be employed to address the issues of data processing speed and parameter estimation in GW signal detection. The only computationally intensive step in this approach is the one-time training phase, which enables low latency detection and faster parameter estimation, making it potentially much faster than other techniques.

Research on the application of deep learning algorithms in gravitational wave (GW) signal detection has been rapidly expanding. In 2017, George and Huerta were the first to apply Convolutional Neural Networks (CNNs) for real-time detection and parameter estimation of GWs using Advanced LIGO data [4]. They generated mock GW signals from binary black hole (BBH) mergers and added them to white Gaussian noise to create simulation data sets. The model accurately classifies signals as GWs or noise, and estimates the source parameters of the detected signals. The proposed deep learning method outperforms the traditional matched-filtering technique currently used by LIGO, particularly in detecting weak and short-duration signals. Their study showed that CNNs had a similar sensitivity to the traditional matched-filtering method, but with much greater speed. Gabbard et al. also conducted a similar study in the same period, comparing the false alarm rate and the receiver operating characteristic (ROC) curve between CNN models and the matched-filtering method, leading to a similar conclusion. Krastev suggests that deep learning models work better on binary neutron star (BNS) mergers than BBH mergers. Variational autoencoders and Bayesian neural networks have also been used for parameter estimation of GW signals, and the long short-term memory network has made progress in the field of GW signal noise reduction, proving that it can effectively remove environmental noise and restore the GW signal under noise. The study also highlights the ability of machine learning to extract challenging source parameters, such as neutron-star tidal deformability, which is important for understanding dense matter and fundamental interactions. Similarly, Yash Chauhan proposed a deep learning approach to improve the detection of weak GW signals using a CNN. The method is trained on simulated data and tested on weak signals from real LIGO data. All these results demonstrate that the proposed deep learning method outperforms traditional matched filtering techniques in detecting weak signals and is robust to noise and different types of time-series data.

Despite the fact that deep learning models, such as Convolutional Neural Networks (CNNs), have been widely used in the field of Gravitational Wave (GW) signal detection. However, most of the existing deep learning models are basic, leaving room for further optimization. However, there is a lack of specific research in this area. To address these issues, our research conducted experiments on the optimization effects of several deep learning techniques for GW signal detection. The results showed that the model with improved techniques outperformed the basic model, achieving higher accuracy and area under curve (AUC) scores. Furthermore, our research focused on the robustness of CNN models on GW signal detection tasks, and our experiments showed that CNN models have good robustness for data of different parameter ranges for masses and spins.

2. Constant-Q Transform

In mathematics and signal processing, the Constant-Q Transform (CQT) and Variable-Q Transform (VQT) are techniques used to transform a data series into the frequency domain. These methods have found applications in various fields. A notable development in this area is an improved version of the CQT that ensures better invertibility. This method involves performing the CQT, using the Fast Fourier Transform (FFT), octave-by-octave. Each octave is processed separately, utilizing lowpass filtered and downsampled results for progressively lower pitches. This approach enhances the accuracy of the transformation. It has been implemented in MATLAB and is also available in the Python library LibROSA. LibROSA takes the subsampled method a step further by combining it with the direct FFT method, which it refers to as “pseudo-CQT.” This hybrid method allows the processing of higher frequencies as a whole, further enhancing the efficiency and accuracy of the transformation. To achieve faster computation of the Constant-Q Transform, the sliding Discrete Fourier Transform (DFT) can be utilized. Unlike the linear-frequency spacing and fixed window size per bin in traditional methods, the sliding DFT offers more flexibility in terms of frequency spacing and window size.Alternatively, the Constant-Q Transform can be approximated by using multiple FFTs with different window sizes and sampling rates across different frequency ranges. These FFTs are then stitched together to create a multiresolution Short-Time Fourier Transform (STFT). In this approach, the window sizes for the multiresolution FFTs are different per octave, rather than per bin.The Constant-Q Transform and its variations find applications in a wide range of fields, including audio and music processing, speech recognition, image processing, and more. These methods provide valuable insights into the frequency content of signals, enabling more effective analysis and processing in various domains.

3. Data Obtaining

To conduct gravitational wave research, the first step is to obtain a suitable dataset for training and testing machine learning models. In this case, the dataset used is a training set of simulated time series data from three gravitational wave interferometers: LIGO Hanford, LIGO Livingston, and Virgo. Each time series in the dataset contains either detector noise or detector noise plus a simulated gravitational wave signal. The simulated signals are generated from 15 randomized parameters, such as masses and sky locations. These parameters enable the creation of diverse simulated signals that represent different types of gravitational wave events. Each data sample in the dataset is stored in an npy file and contains three time-series, one for each detector. Each time-series spans 2 seconds and is sampled at 2,048 Hz. This high sampling rate is necessary to capture the high-frequency nature of gravitational waves. The integrated signal-to-noise ratio (SNR) is classically the most informative measure of a signal’s detection, and a typical level of detectability is when this integrated SNR exceeds ~8. This means that the simulated gravitational wave signals in the dataset have a minimum SNR of 8, which ensures that they are detectable and can be used for training and testing machine learning models. Overall, obtaining a suitable dataset with a diverse range of simulated signals is crucial for training machine learning models to accurately detect and classify gravitational wave signals in real-world data from interferometers.

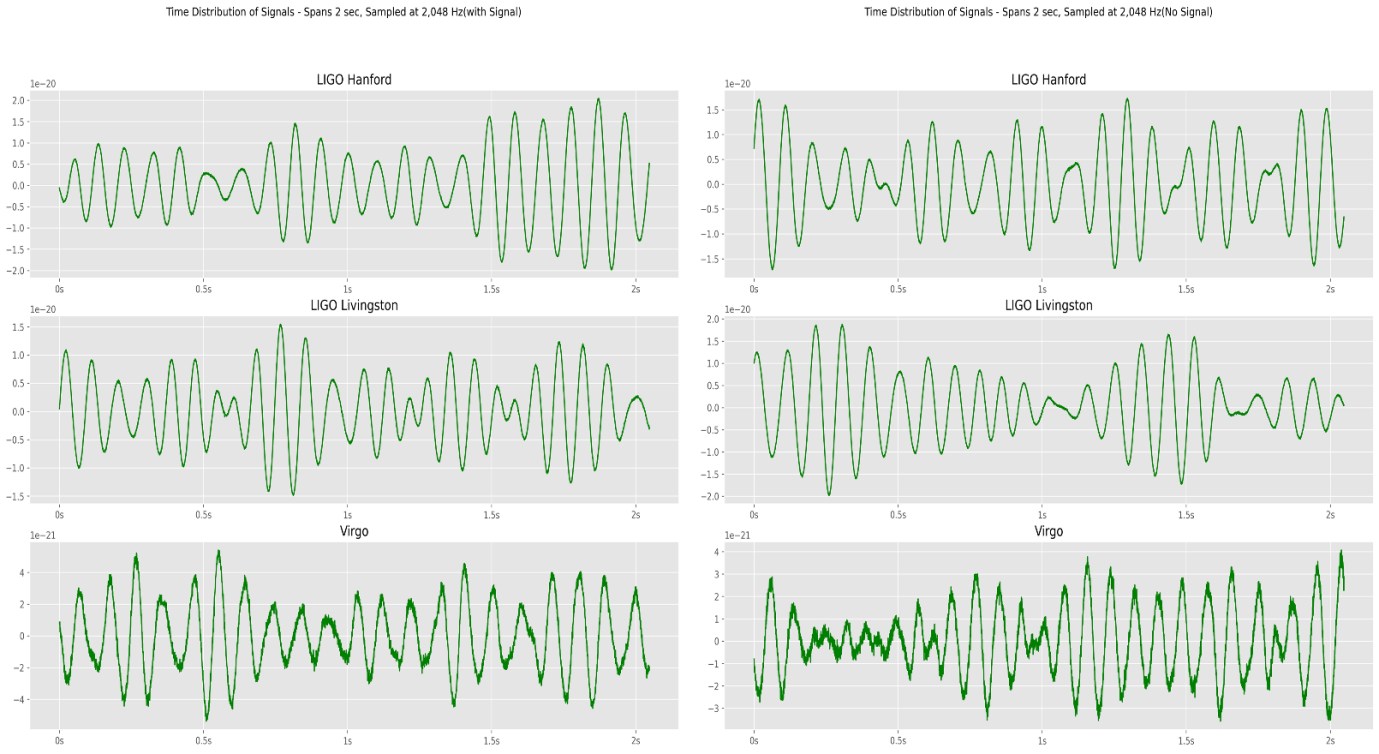
Figure 1. Time distribution of gravitational wave signal. Left: with signal. Right: pure noise [5].

4. Data Processing

4.1. Fast Fourier Transform and Constant Q-Transform

Fast Fourier Transform (FFT) is a popular method for signal processing that transforms a signal from the time domain to the frequency domain. It decomposes a signal into its component frequencies and their relative amplitudes. The FFT algorithm computes the Discrete Fourier Transform (DFT) of a sequence in a fast and efficient way. It is commonly used to analyze stationary signals with periodic components, such as audio signals or images, and is particularly useful for filtering out noise at specific frequencies.

In contrast, Constant Q-transform (CQT) is a method for signal processing that analyzes signals in the frequency domain using logarithmic frequency scales. This logarithmic scaling makes CQT a more natural choice for analyzing signals with non-linear characteristics, like those found in gravitational wave signals. In comparison to FFT, CQT preserves more non-linear information in the signal, which can better simulate the real signals.

One significant difference between FFT and CQT is the type of signals they are best suited for analyzing. FFT is useful for analyzing stationary signals with periodic components, while CQT is better suited for analyzing non-stationary signals like gravitational waves. Gravitational wave signals are non-stationary signals because they have a varying frequency over time. In addition, FFT assumes that the signal is evenly spaced in time, while CQT can handle signals with uneven time spacing.

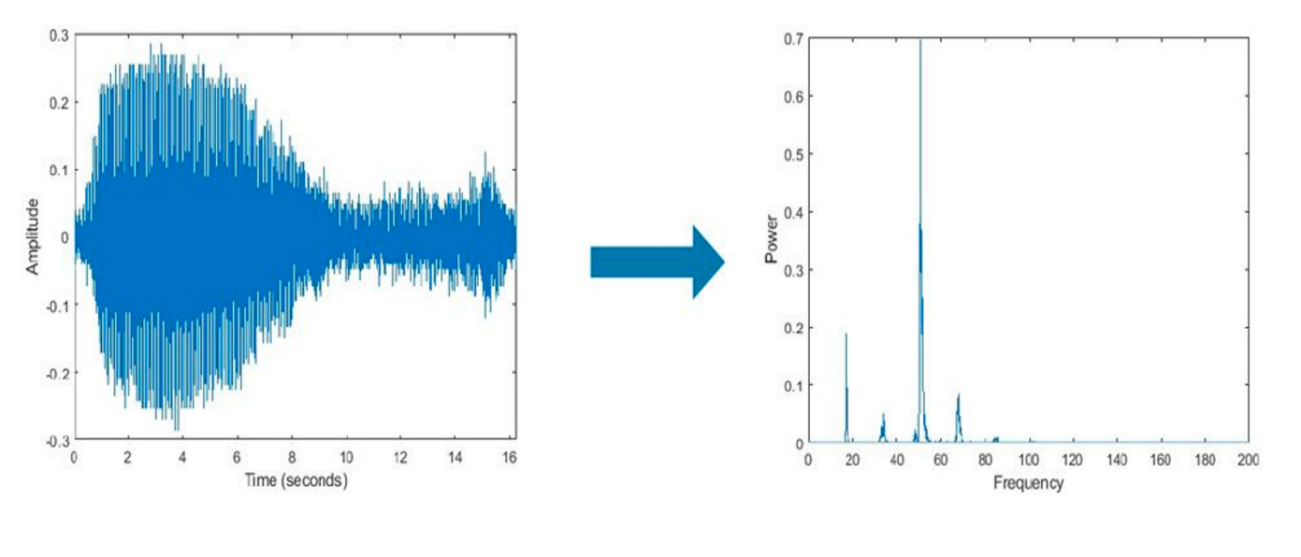
Figure 2. An audio signal decomposed into its frequency components using FFT [6].

Overall, both FFT and CQT are useful methods for signal processing and have their strengths and weaknesses depending on the type of signals being analyzed. In the context of gravitational wave research, CQT is particularly useful for denoising because it is well-suited for analyzing non-stationary signals like those from gravitational waves.

Figure 3. Constant Q transforms [7].

4.2. CNN models and pre-trained models

Figure 4. An overview of system framework.

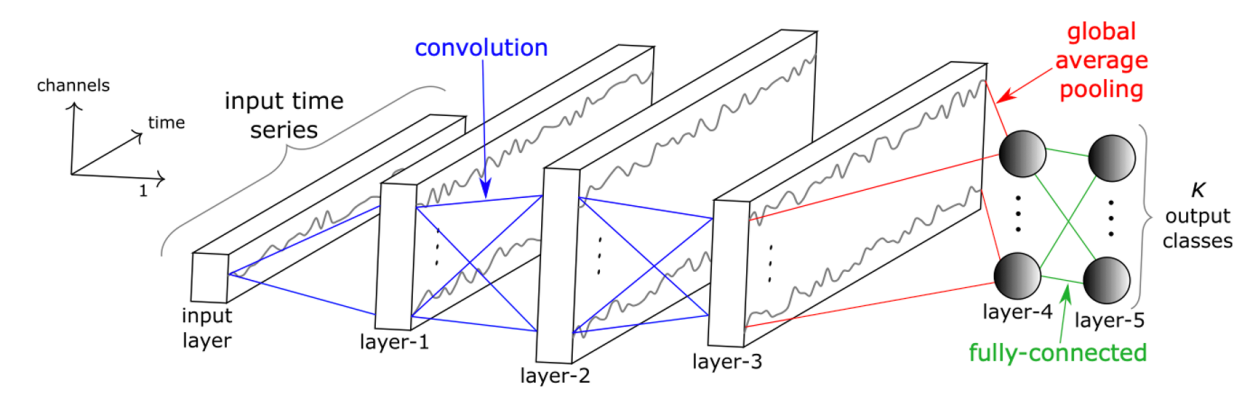
Figure 5. Convolutional Neural Network architecture with fully connected layers.

For our gravitational wave research, I explored three different models. Initially, I considered the gravitational wave signals as time-series data and attempted to use a 1D CNN binary classification model, with FFT added for denoising. However, this approach did not yield the desired results. I then turned to CQT as the denoising approach, as it is better suited for analyzing non-periodic signals and capturing non-linear information. By applying CQT, the original data shape of 3*4096 changed to 369*65. I used a 2D CNN model with CQT for denoising and obtained a significant improvement in performance.

Despite the success of the second model, I wanted to explore other possibilities and decided to load EfficientNet B7, a pre-trained model that achieves new state-of-the-art 84.4% top-1 / 97.1% top-5 accuracy on ImageNet. I combined the pre-trained model with CQT and a 1D CNN for binary classification, resulting in further improvements in performance.

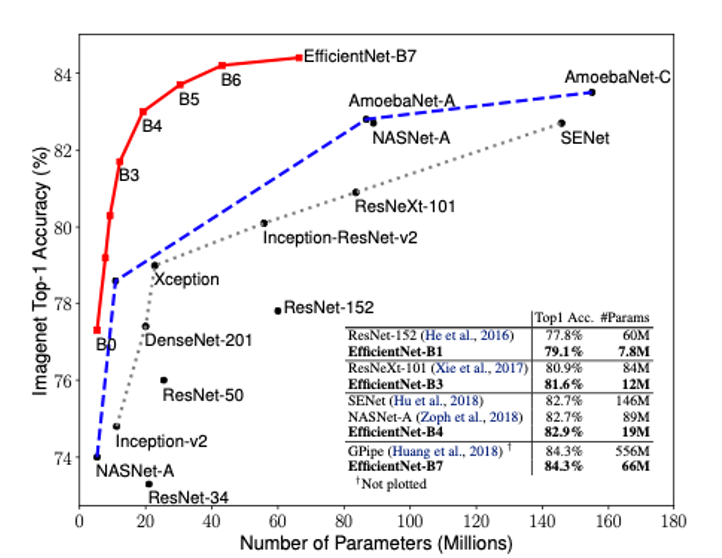
Figure 6. EfficienNet Comparison with other pre-trained models [8].

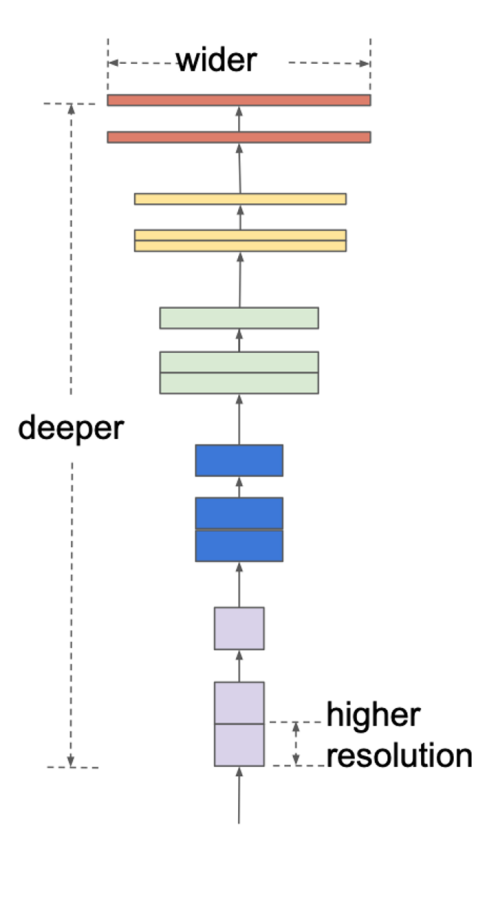
Figure 7. A compound scaling method of EfficientNet uniformly scales all three dimensions with a fixed ratio.

In addition to model selection, I also tuned hyperparameters to optimize performance. The learning rate is a crucial hyperparameter, and its value significantly affects the model’s performance. Additionally, the number of epochs trained impacts performance. Further tuning of other hyperparameters was necessary to achieve the best possible model performance.

5. Results and Conclusion

The results of the three models are presented, and it is evident that the CQT +EFN + 1D CNN (GravNet) model has the highest validated accuracy of 0.7652 and AUC of 0.8503, followed closely by the CQT + 2D CNN model with a validated accuracy of 0.7742 and AUC of 0.8438. On the other hand, the FFT + 1D CNN model showed a significantly lower validated accuracy of 0.5000 and AUC of 0.5001, indicating that it did not perform well.

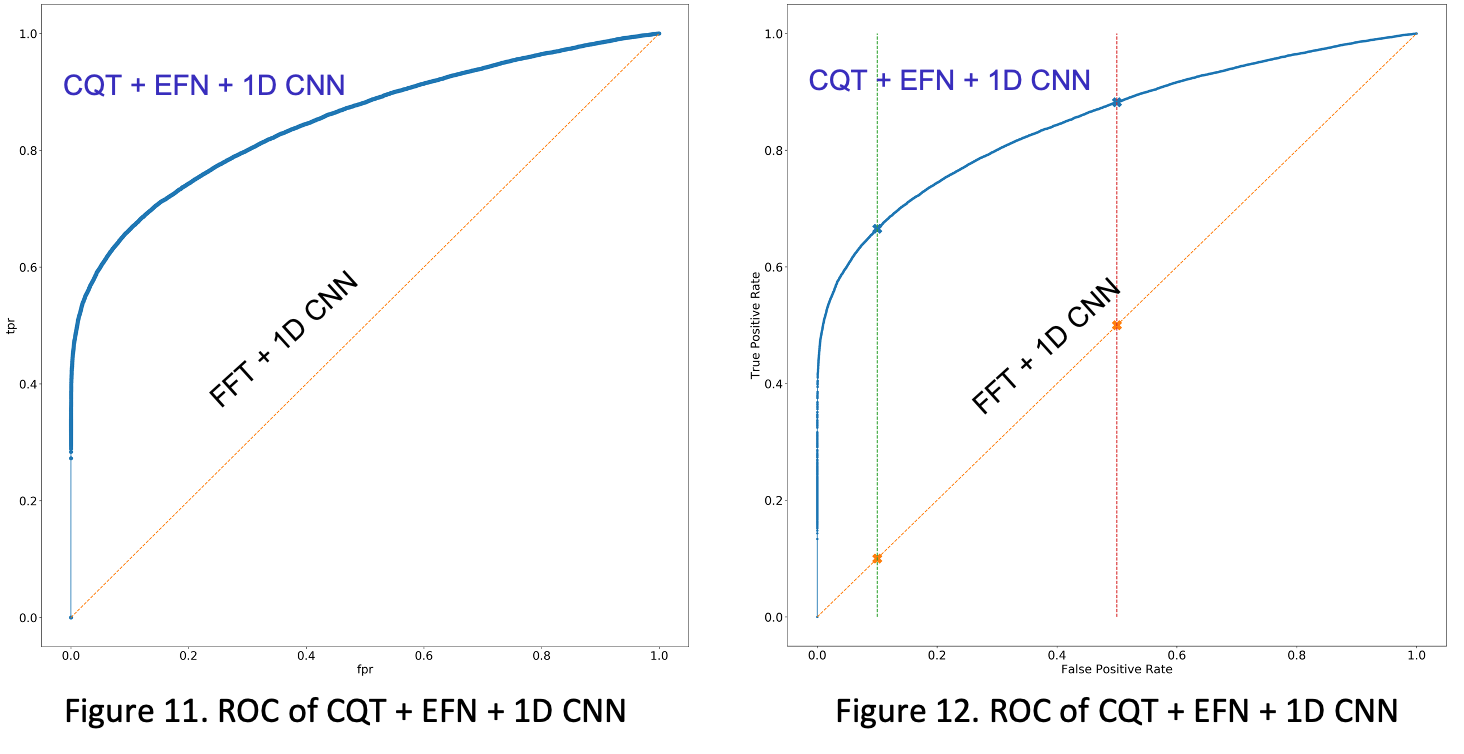
Figure 8. ROC of CQT+ 2D CNN (left) and ROC of of CQT + EFN + 1D CNN (right).

Direct comparison shows that CQT+EFN+1D CNN has the best performance while FFT+1D CNN has the worst. Through this result, the combination of the denoising approach and convolutional neural network played an important role. Due to the unideal AUC of 0.5001 of FFT+1D CNN, I concluded that The CQT is more effective in capturing signal characteristics in gravitational wave data. In contrast, the FFT may not capture the complex time-frequency patterns of the signal as effectively.

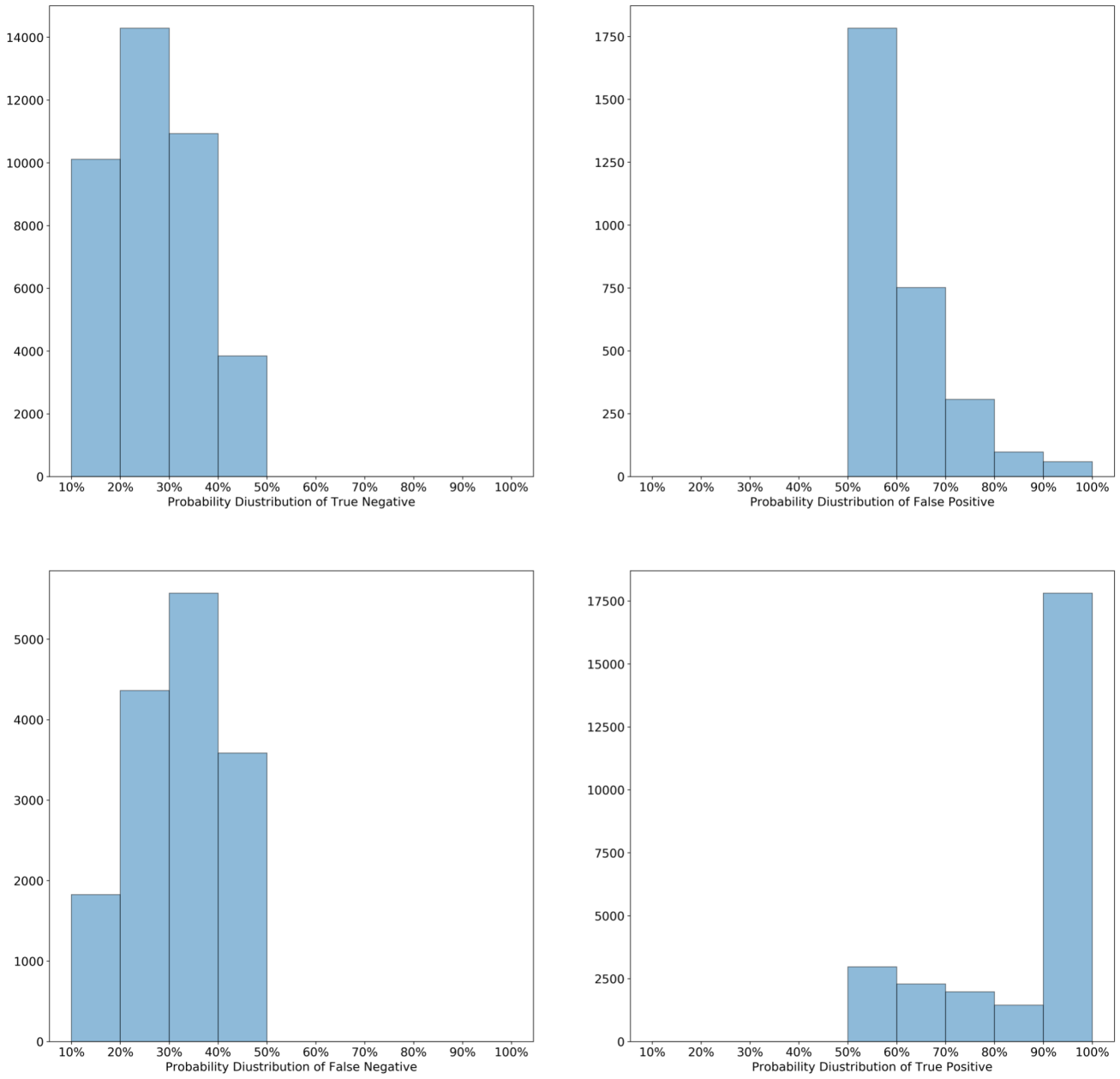
Figure 9. Probability distribution for true positive, true negative, false positive, and false negative.

Moreover, the number and complexity of the hyperparameters in each approach may also contribute to the observed differences in performance [9]. CQT + EFN + 1D CNN uses a combination of several techniques that are all known to be effective for processing and classifying image and time-series data. The use of EfficientNet-B7, a state-of-the-art convolutional neural network architecture, may have contributed to the high accuracy and AUC scores. The CQT + 2D CNN model uses a similar approach as the first one but replaces the 1D convolutional layers with 2D convolutional layers.

However, the AUC score is lower than the first one, which could be due to the use of 2D convolutional layers not being as effective in this particular problem as 1D convolutional layers in terms of analyzing times eries data. FFT + 1D CNN model only uses Fourier Transform and 1D convolutional layers, which may not be sophisticated enough. Moreover, the use of EfficientNet doesn’t make another big leap from the 2D CNN results.

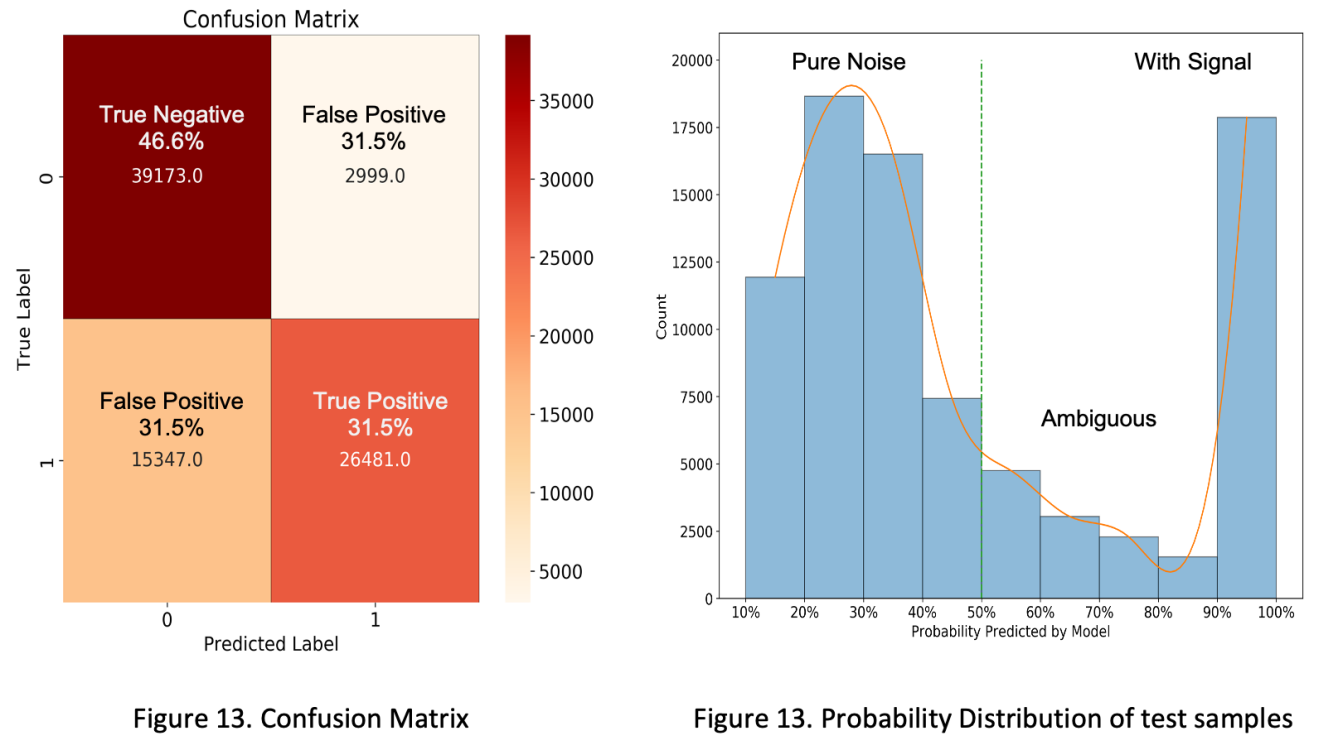
Figure 10. Confusion matrix (left). Probability distribution of test samples (right).

6. Future Studies

To further evaluate the performance of our data analysis method, we will apply it to real LIGO/VIRGO data. As our training and test data only last a few seconds each, this will provide a more realistic assessment of its effectiveness. Additionally, we plan to enhance our code with new features, including GW signal classification. Specifically, we aim to distinguish between GW signals from BH-BH mergers, BH-NS mergers, and NS-NS mergers, which will add valuable astrophysical insight to our data analysis. Finally, we will use our trained model to search for GW candidates in the LIGO/VIRGO data, leveraging our understanding of existing patterns of GW signals to identify potential signals with a lower probability of occurrence.