1. Introduction

Traveling Salesman Problem (Application of ant algorithm in solving TSP problems) requires the shortest route to travel a series of cities and then return to the initial point and has model features in many branches of mathematics, computer science and operations research [1, 2]. Although the problem statement seems simple, the Traveling Salesman Problem is a combinatorial optimization problem classified as NP-hard [2-4], and one of the classic problems in combinatorial optimization, computer science, whose solution will grow exponentially with the increase in the number of cities, and so far, no fully effective algorithms have been found for the TSP problem. However, in recent years, people have accumulated a large number of algorithms through continuous research, and in summary, The two main categories of contemporary algorithms are modern intelligent optimisation algorithms and classic optimisation algorithms. While modern intelligent optimisation algorithms derive from a variety of sources, including genetic algorithms, simulated annealing algorithms, ant colony algorithms, forbidden search algorithms, greedy algorithms, neural network algorithms, and so on, traditional optimisation is primarily divided into two directions: complete algorithms and approximate algorithms. The TSP problem, due to its combinatorial nature, can be solved using the exhaustive method when the number of cities is small, but as the number of cities increases, the solution space of the problem expands dramatically and the exhaustive method becomes inapplicable. Therefore, heuristic algorithms are needed to solve the larger-scale TSP problems.

In recent years, people's research on the ACO algorithm shows that the ACO algorithm has the characteristics of a positive feedback mechanism, heuristic probabilistic search, and distributed computational method, and it is still one of the best algorithms to solve the TSP problem compared to annealing algorithm or genetic algorithm.

2. Literature Review

2.1. Origin and Development of Ant Colony Algorithm

Ant Colony Algorithm (ACO) is an algorithm designed in nature based on the behavioral patterns of ants while searching for food, Ants move according to the amount of pheromone, the richer the amount of pheromone on the path, the more likely other ants are to follow it [5]. Shorter paths have more pheromones, so ants may tend to choose shorter paths, this experiment was demonstrated in the Twin Bridges experiment [6,7]. (As shown in Figure 1) Through this process, ants eventually find the shortest path. It was originally proposed by the Italian scholar M. Dorigo, who further elaborated the basic idea of the ACO algorithm in his PhD thesis in 1992 [8, 9].

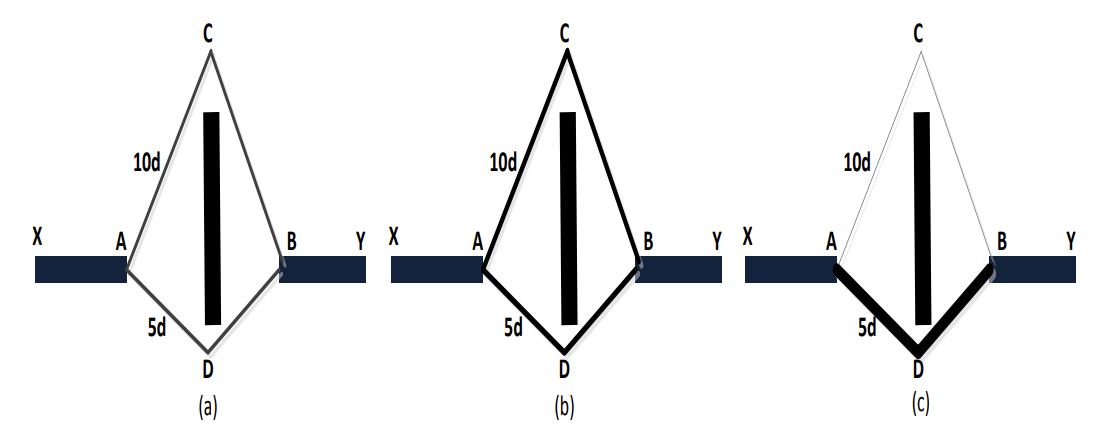
Figure 1. The basic schematic diagram of the ant colony algorithm

The advantage of the ACO algorithm is that it can avoid falling into local optimal solutions and can adaptively adjust the probability of path selection. In addition, the ant colony algorithm also has distributed solution characteristics, i.e., multiple ants search at the same time, which can accelerate the solution process.

The ant colony algorithm's fundamental idea is this:

Ants on the path first release pheromones.

Secondly, they choose a course at random when they get to an intersection, they haven't previously crossed. The path length-related pheromone is released concurrently.

Third, the relationship between pheromone concentration and path length is inverse. When the intersection recurs, subsequent ants select a path with a larger concentration of pheromones.

Next, on the ideal path, the concentration of pheromones rises.

The colony eventually determines the best route for locating food. Suppose there are n cities and i, j, n, m is the number of ants. The probability of ant K moves from node i to node j:

\( p_{ij}^{k}(t)=\begin{cases} \begin{array}{c} \frac{τ_{ij}^{α}(t)∙η_{ij}^{β}(t)}{\sum _{s∈{allowed_{k}}}τ_{ij}^{α}(t)∙η_{ij}^{β}(t)} {j∈allowed_{k}} \\ 0 otherwise \end{array} \end{cases} \) (1)

ηij(t) is the reciprocal of the distance between i and j. τij(t) shows the amount of information on the path between city i and city j. ηij(t) is the reciprocal of the distance between i and j. τij(t) shows the amount of information on the path between city i and city j.

α: represents the relative importance of path trajectory.β: represents the relative importance of path visibility.

allowedk is the set of paths that the kth ant can choose next under the premise of satisfying the 3 conditions of the artificial ant behavior law.

The global update rule is implemented as follows. Once all the ants have established their traveling group, the pheromone is based on the following equation:

\( {τ_{ij}}(t+n)= ρ ∙{τ_{ij}}(t)+ \sum _{k=1}^{m}∆τ_{i}^{k} \) (2)

M. Dorigo has proposed three computational models, they are ant-cycle system, ant-quantity system and the ant-density system, among which the latter two models are for local information, while the former utilizes global information [10]. Through experimental comparison, the ant-cycle system has better performance in solving the TSP problem, and thus it is used as the basic model in this paper.

\( ∆{τ_{ij}}=\begin{cases} \begin{array}{c} Q/{L_{k}} \\ 0 \end{array} \end{cases} \frac{ if(i, j)∈tour done by ant k}{otherwise} \) (3)

2.2. Algorithm Description of the Ant Algorithm for Solving the TSP Problem

As per the preceding introduction, every ant leaves a pheromone on the branch (i,j) it passes through on its way around. The distance between cities and the pheromone residual present on the currently linked branch influences the likelihood that an ant will select a city. The ants are prevented from visiting the cities they are visiting until after they have made one legitimate peripatetic journey (this can be managed by the taboo table). This is done to force the ants to make these journeys. This is the flow of the ACO algorithm to solve the TSP problem:

(1) Initialization:t=0, nc=0, τij (t)=C, Δτij=0, and place m ants on n cities. Where nc is the number of iterative cycles, t is a "pseudo" time control variable.

(2) Place the initial starting point of each ant in the current solution set visited-city; for each ant k (k=1, 2, ..., m), place m ants on n cities. , m) move to the next vertex j with probability pkij, and place j in the current solution set visited-city.

(3) Calculate the objective function value Lk for each ant (k=1, 2, .... , m) and record the current best solution.

(4) Update the pheromone concentration of each edge according to the pheromone concentration adjustment rule.

(5) For each edge (i,j), set Δτij=0,nc=nc+1.

(6) If nc<NC and there is no degenerate behavior (i.e., all the solutions found are the same), then skip to step (2). Otherwise, end and output the current best solution.

2.3. Different Parameter Analysis of ACO

The five parameters that make up the ant colony algorithm are Q, C, α, β, and ρ. Every parameter significantly affects how well the algorithm performs. According to the majority of academics, the optimal experimental outcomes for the ant-cycle model are m=n, 0≤α≤5, 0≤β≤5, and 0.10≤ρ≤0.99. The significance of the remaining information in each node is indicated by the value of α; that is to say, the higher the value of α, the higher the likelihood that ants will select the previously travelled path. The value of β indicates how much the heuristic information is appreciated; a high value of α will, however, force the search to end too soon in a local minimum solution. The ants choose the city close to it increases with the increase of β value; ρ represents the volatilization degree of pheromone (retention rate), and its value is very important, if it is not taken appropriately will get poor results.

According to the above analysis, the study of the optimal configuration of the parameters α, β, ρ is of great significance to play the role of ant algorithm in practical problems.

However, in addition to the three parameters α, β, ρ, the number of ants M and the total information Q also have some influence on the algorithm.

In addition, regarding the effect of the size of the number of ants m on the number of cycles (convergence performance) of the ant algorithm, when the number of ants is too large, the stability and global nature of the search will be improved, although the convergence speed will be slower.

3. Analysis of Ant Algorithm for Solving TSP Problem

Through the experiment to apply the ant algorithm to solve the data set bayg29, data from bayg29, this paper through the selection of different parameters, through the program written by MATLAB calculations, due to the results of each program run bbeing different, each different parameter I will run 5 times, take the smallest value to put in the table and record.

Number of cities N=29, number of ants M=20, Q=1000 to examine the effect of parameter ρ on the results:

Table 1. Effect of ρ on optimal path

Controlling for α, ρ, consistently, the effect of the parameter β on the results was examined:

Table 2. Effect of β on optimal path

Controls β, ρ were consistent and the effect of parameter α on the results was examined:

Table 3. Effect of α on optimal path

From the above data, it can be seen that under certain parameters M, C, and Q, for the parameters α and β that affect the size of the probability of the ant's next path selection, the β parameter is the one that mainly affects the performance of the algorithm, the α parameter's impact on the algorithm's convergence result is secondary, and the residual factor ρ of the pheromone concentration has a relatively small impact on the performance.

The number of cities is constant, the parameters α, β, and ρ are constant, Q = 1000, and the effect of the number of ants M on the results is examined:

Table 4. Effect of M on optimal path

It can be found that the value of M does not have a very significant effect on the data results, but for the convergence results are improved.

4. Conclusion

This paper focuses on the Ant Colony Algorithm and the solution to the TSP problem. Each variable is analyzed for the overall algorithm performance. Through the experimental results, This tell that the program based on this algorithm is able to solve the Traveling Salesman Problem with high performance, however, there are many challenges in parameter tuning that still need to be addressed in the future. The data used in this experiment is data set bayg29, and the number of cities is 29. However, more city data are not used in this experiment, so the influence of the number of cities on the optimal path is not tried. For the TSP problem, there may be more algorithms in the future, and the TSP problem may get better solutions.