Strategic flight planning models based on integer programming: Optimizing air traffic and airport capacity

Zhijian Ye; Qin Pang; Luodan Hu

doi:10.54254/2755-2721/65/20240502

1.Introduction

With the rapid development of the civil aviation industry and the substantial growth of the domestic economy, the annual increase in flight volume has posed new challenges to air traffic management. Particularly in the context of limited airport capacity, the imbalance between the growing demand for flights and limited airport capacity has become a critical issue in aviation operations. According to the Civil Aircraft Market Forecast Report for China (2022-2041), it is predicted that by 2041, the average annual growth rate of China’s air passenger turnover will reach 7.7%, accumulating to 2.9 trillion passenger-kilometers. This growth trend results in increased air traffic, higher probabilities of flight delays, thereby reducing the overall operational efficiency of the entire traffic network. The cascading effects of flight delays significantly impact airlines, passengers, and airports. Flight delays or cancellations not only increase the workload of air traffic control departments but also incur additional costs for aircraft maintenance management and passenger services. For passengers, these delays or cancellations disrupt travel plans, causing economic and emotional losses, severely affecting the passenger travel experience. Simultaneously, airports face problems of flight congestion on the ground apron and passenger accumulation in waiting halls, further reducing airport operational efficiency. Therefore, there is a need to consider how to balance air traffic demand and capacity to reduce flight delays effectively.

Currently, the primary consideration for addressing traffic demand and capacity issues revolves around the day-of-flight operational conditions, including gate assignments [1-3], flight sequencing [4,5], ground waiting [6,7], etc. At the strategic level, the Civil Aviation Administration of China (CAAC) has achieved centralized processing of flight plans in the strategic phase, effectively improving data quality and operational efficiency [8]. Kammoun et al. [9] proposed a method for flight plan rearrangement in their study to enhance the efficiency of air traffic flow. Using a discrete event system approach, they optimized airspace utilization and reduced flight delays by rearranging flight plans. Jacquillat and Odoni [10] introduced a comprehensive approach to addressing airport congestion, developing a new iterative solution algorithm to solve airport congestion issues by adjusting airline schedules. Li Yinfeng [11] researched a qualitative analysis method for the influencing factors of terminal airspace capacity and established a capacity assessment model for the terminal area. They predicted strategic traffic demand and capacity requirements, allowing effective management and utilization of limited airspace capacity. Tatjana [12] proposed an integer programming model for strategic reallocation of flights, considering the entire transportation network (including airports and sectors) and addressing the handling of large-scale strategic flight plans. The evaluation of the strategic results based on the presented data indicates that, when formulating flight schedules several months in advance, early arrangement of flight plans can effectively reduce flight delays. Starita et al. [13] further studied the impacts of more robust capacity planning, considering uncertainty in both traffic and capacity provisions. Yan Xu et al. [14] proposed a novel method for achieving demand-capacity synchronization within a collaborative air traffic flow management framework. This method takes into consideration the constraints of airspace sectors and discusses the proposed approach from the perspectives of adjusting aircraft speeds in the airport network and releasing times in airspace sectors. The results indicate a significant reduction in the occurrence of flight delays or cancellations, along with an improvement in the operational efficiency of airport terminals. Given the uncertainty and randomness of weather, Kicinger et al. [15] treated weather as a stochastic factor, exploring flight cooperation capabilities under different weather conditions when airport capacity is fixed. Zhang Jing [16] conducted a study on the capacity assessment influenced by weather seasonality and types. The proposed method and research theoretical model, based on weather forecast for capacity assessment, fill the domestic gap in understanding the impact of weather on airspace capacity, enhancing the research model that balances traffic demand and capacity. We Wei et al. [17] conducted a study on the impact of adverse weather conditions in complex networks on flight delays. Simultaneously, they calculated the probability of delays and the number of delayed flights between airports of different levels to assess the extent of the ripple effect of delays on other airports during adverse weather conditions. This reflects the influence of adverse weather on the aviation network. Wang Nan [18], utilizing the routine aviation weather reports and historical flight information data from Urumqi Airport for the years 2014 to 2017 at half-hour intervals, employed relevant data decomposition preprocessing methods and constructed a decision tree model. This resulted in the establishment of a meteorological factor database affecting flight delays, enabling the quantification of the impact of adverse weather on the punctuality of departing flights from Urumqi Airport. Additionally, in recent years, military aviation activities in certain regions have become increasingly complex, sophisticated, and normalized. For example, within the Lanzhou control area, military aviation activities occur for over 90% of the year, with the control authorities issuing Notices to Airmen (NOTAMs) for more than 70% of the time due to military aviation activities. The complexity of military aviation activities imposes significant restrictions on the use of airspace for civil aviation, including large restricted areas, multiple altitude restrictions, and extended restriction periods. This complexity increases the difficulty of coordination and command work for civil aviation control departments and adds to the workload of air traffic controllers [19]. When military aviation activities are unavoidable, flexible use of airspace can minimize sector capacity losses.

Previous studies have predominantly approached air traffic management from the perspective of flow management, addressing issues on a tactical level. However, in the domestic context, the balance between traffic demand and capacity has not been adequately addressed from the strategic level of flight planning. This paper, considering strategic flight plans in conjunction with the strategic aspect of flight operations, aims to balance traffic demand and capacity. In summary, departing from a strategic perspective, this paper analyzes the impact of weather and military activities on flight delays or cancellations. By formulating strategic flight plans, the objective is to achieve an effective balance between traffic demand and airport capacity, ensuring the safety, orderliness, and efficient operation of air traffic. This not only contributes to reducing costs for airlines and passengers but also enhances overall operational efficiency and the travel experience for passengers.

2.Strategic Flight Plan Formulation and Implementation Process

2.1.Establishment of the Joint Operations Management Center

To enhance airport operational efficiency, ensure accurate flight scheduling, and guarantee flight safety and smoothness, it is recommended to establish a Joint Operations Management Center. The core function is to consider flight plans in conjunction with uncertain factors such as airport capacity and weather, as shown in Figure 1. The composition of this center includes the origin airport group, destination airport group, air traffic control bureau of the origin airport location, air traffic control bureau of the destination airport location, and the person in charge of implementing strategic flight plan adjustments from the airline responsible. The center’s structural design comprises three specialized working groups: the Support Group, Meteorological Group, and Clearance Group, aiming to achieve professional and efficient management.

Core Responsibilities of the Center: The main task of the center is to coordinate the management activities of the three working groups, collect flight plan data reported in advance by airlines, and input this data into the strategic flight plan formulation model proposed in Section 2.2. The output results of the model will be fed back to the airlines to aid them in compiling the final flight schedule based on the ultimate decision.

Responsibilities of the Support Group: The Support Group is responsible for maintaining the daily operations of the origin and destination airports. They collect and organize relevant information about airport, airline, and passenger support, update and upload information in real-time, allowing relevant units to promptly understand the operational dynamics of airports and flights.

Responsibilities of the Meteorological Group: The Meteorological Group, composed of meteorological personnel from both the departure and destination airports, utilizes technologies such as big data and cloud computing for inter-regional meteorological analysis, facilitating collaborative construction and sharing of meteorological data. Through inter-regional meteorological communication and coordination, the meteorological group is dedicated to enhancing the accuracy of weather assessments and providing decision-making support for adjusting strategic flight plans.

Responsibilities of the Clearance Group: The Clearance Group is responsible for coordinating the ground support work at the origin and destination airports after implementing adjustments to the strategic flight plan. They ensure timely sharing and timeliness of information. This group maintains close communication with the airline’s operations control department, tracks the real-time flight dynamics, compiles the collected information, and uploads it to relevant units to assist in the smooth implementation of adjusted strategic flight plans.

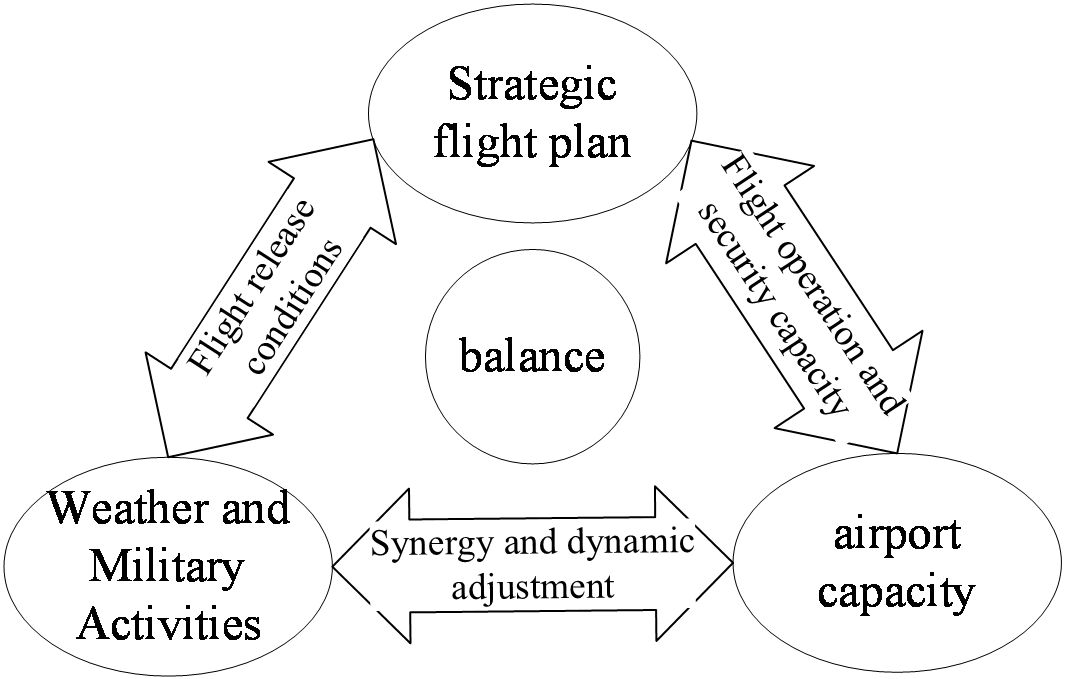
/word/media/image1.emf

Figure 1. Strategic Flight Plan Management Mechanism Chart

2.2.Strategic Flight Plan Formulation Process

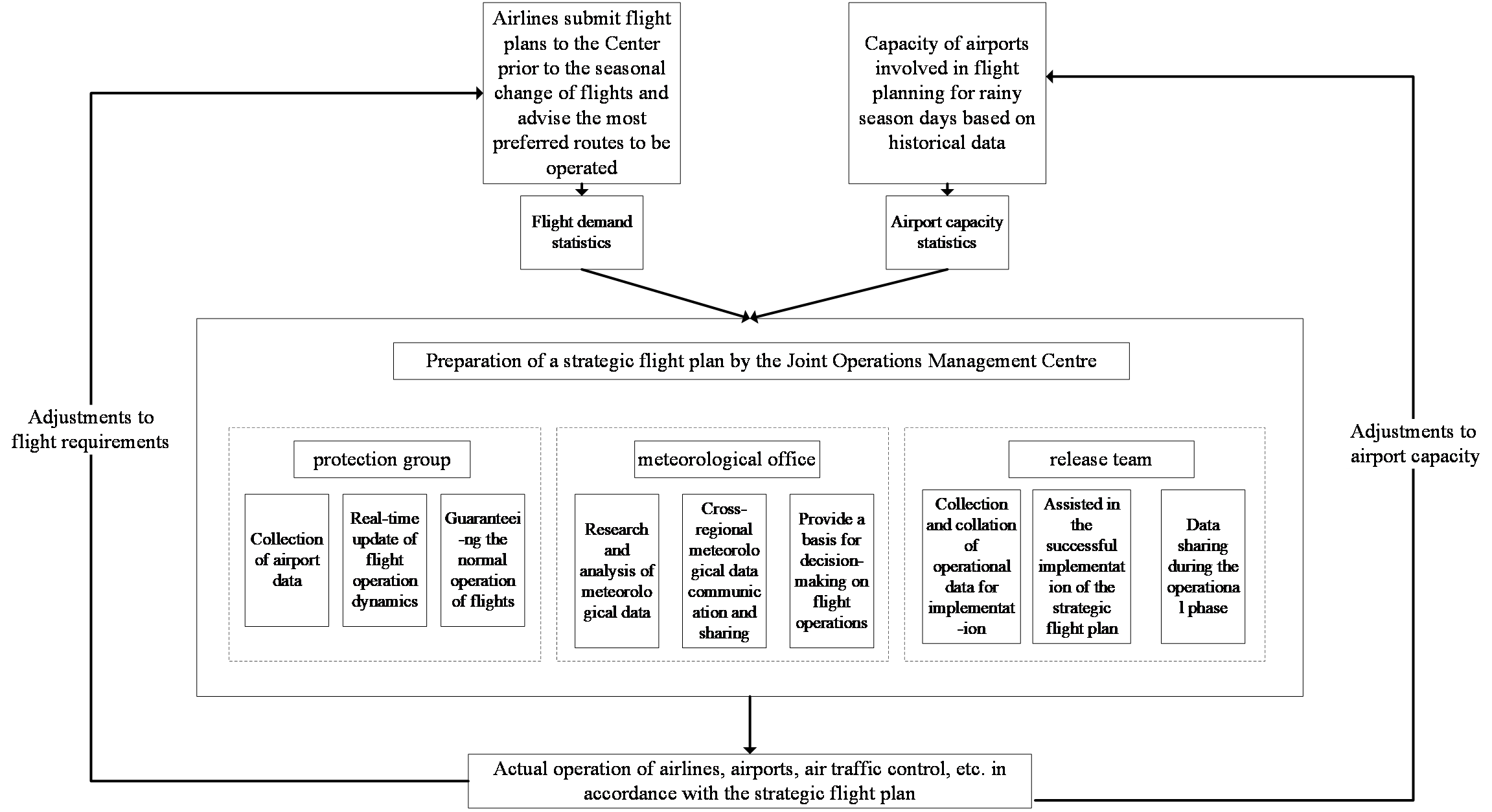
/word/media/image2.emf

Figure 2. Strategic Flight Plan Implementation Process

Implementation Steps of the Strategic Flight Plan:

Step 1: Several months before operation, airlines submit flight information, routes, departure/arrival times, various operational costs, weather information at departure/destination airports, alternative routes, and aircraft types to the Joint Operations Management Center. They also inform the center of their preference for a specific route. The relevant personnel from the Meteorological Group negotiate and assess the weather at the origin and destination airports.

Step 2: The Joint Operations Management Center calculates the adjusted strategic flight plan using the proposed model, and the results are then communicated back to the airlines.

Step 3: After receiving the final strategic flight plan, the corresponding airline officials are informed. They are asked whether they agree to change the original flight schedule. If agreed, the plan is submitted to the air traffic control department, and approval for the route change is requested.

Step 4: The Joint Operations Management Center, considering the operating principles of the current flight schedule, comprehensively evaluates the operational weather conditions at the origin and destination airports for the day. It also considers factors like military activities and compiles the final flight schedule based on the airline’s agreement to implement the strategic flight plan.

Step 5: The Joint Operations Management Center signs a notification agreement with the airlines, Shuangliu Airport, Tuofeng Airport, and Mangshi Airport, indicating unanimous operational consent for the final strategic flight plan.

Step 6: Airlines and airports execute flight support tasks as per the strategic flight plan.

Step 7: On the day of operation according to the strategic flight plan, the information about relevant flight details, such as departure and arrival times, is displayed on the boarding gate screens or communicated to passengers manually.

Step 8: The Joint Operations Management Center collects feedback from airlines, Shuangliu Airport, Tuofeng Airport, Mangshi Airport, and passengers on the operational schedule and support services of the flight. This feedback is then analyzed and summarized.

3.Formulation of the Strategic Flight Plan Model

3.1.Model Symbol Annotations

Table 1. Model Variables and Explanations:

Variable	Explanation
\( A \)	Flight set, indexed by\( a \)
\( B \)	Airport set, indexed by\( b \)
\( C \)	Aircraft type set, indexed by\( c \)
\( D \)	Aircraft type used for flight execution\( a \)
\( E \)	Origin-Destination (OD) pair set, indexed by\( e \)
\( F \)	OD pairs connected by flights\( a \)
\( G \)	Sector set, indexed by\( g \)
\( H \)	Route set, indexed by\( h \)
\( h_{e}^{c}∈H \)	Possible route set for flights between OD and\( c \)-type aircraft
\( I \)	Number of elements (airports) along the route\( h \)
\( J \)	Element\( i \)of Route\( h \)(airports)
\( K \)	Set of flight actions,\( K=\lbrace ent,dep,arr,tot\rbrace \), where\( ent \)indicates entering a sector,\( dep \),\( arr \), and\( tot \)correspond to takeoff, landing, and total (i.e., either takeoff or landing) airport maneuverability, respectively
\( L \)	A set of time periods considering flight actions
\( M \)	Element set\( G∪B \)(airports), indexed by\( m \)
\( N \)	Set of hours, indexed by\( n \)
\( O \)	A set of time periods in\( n \)hours, where element\( m \)is active.
\( P \)	The maximum number of flight operations (i.e., capacity) that may be performed on element\( m \)for action\( k \)within\( n \)hours.
\( R \)	Requested departure time for flight\( a \)
\( S \)	Requested arrival time for flight\( a \)
\( T \)	Time window for flight\( a \)along route\( h \)
\( U \)	Origin airport OD pair\( e \)
\( V \)	Destination airport OD pair\( e \)
\( W \)	Flight time from the origin to the\( i \)element of route\( h \)

3.2.Objective Function

The decision variables of the strategic flight plan model are defined as follows:

\( x_{h}^{a}(t)=\begin{cases}\begin{matrix}1;flight a departs at time t along route h. \\ 0;else. \\ \end{matrix}∀a∈A,h∈h_{e}^{c},t∈T\end{cases} \)

(1)

The objective functions of the strategic flight plan model are as follows:

(1) Flight Minimum Shift (FMS) Function:

The minimization objective is calculated by summing the negative departure offsets and positive arrival offsets for each aircraft. This approach avoids the double counting of offsets propagated from departure to arrival or from arrival to departure. The goal is to minimize the total sum of offsets for all flights, fulfilling the requirements of the flight scheduling arrangement.

\( \sum _{a∈A}(\sum _{h∈h_{e}^{c}}x_{h}^{a}(t)•(max{\lbrace R-t,0\rbrace }+max{\lbrace R+t+W-S,0\rbrace }{)^{1+{ε_{1}}}}) \)

(2)

At this point,\( W \)is\( i∈[1,I] \).\( {ε_{1}} \)is introduced to ensure fairness in the allocation of the strategic flight plan. The objective function incorporates a cost coefficient to guarantee fairness, and\( {ε_{1}} \gt 0 \)approaches zero.

(2) Flight Minimum Cost (FMC) Function:

The cost minimization objective aims to substantially reduce the strategic operational costs of flights, including ground and air operation costs as well as in-flight expenses.

\( Min\sum _{a∈A,h∈H_{F}^{D},t∈T}c_{D}^{H}(|t-R|{)^{1+{ε_{2}}}}•x_{h}^{a} \)

(3)

Among them, the strategic cost per\( τ \)minutes of operating flights along route\( h \)for aircraft type\( c \)is defined as follows:

\( C_{c}^{h}(τ)=cos{t}ga1•τ+cos{t}ga2•W+cos{t}ga3 \)

(4)

Where,\( cos{t}ga1 \)represents the land-side cost per minute for aircraft type\( c \), including ground maintenance, fleet, and crew usage costs.\( cos{t}ga2 \)represents the air-side cost per minute for aircraft type\( c \), including onboard maintenance, fleet, crew usage, and fuel costs.\( cos{t}ga3 \)represents the route fee for flights operated by aircraft type\( c \)along route\( h \), calculated as the product of distance factor, weight factor, and the unit rate defined by the Civil Aviation Administration’s route fee settlement center. To ensure fairness, the same approach as used in the FMS objective function is adopted by scaling up the flight cost to\( {ε_{2}}+1 \)and approaching zero for\( {ε_{2}} \gt 0 \).

3.3.Constraints

This model will be applied in the strategic phase, before the publication of the flight schedule. The departure or arrival times may deviate earlier or later than the requested times to avoid excessive substitutions. The maximum allowable substitution is either an earlier or later departure or arrival time. Assuming no flight cancellations, the flight time for each route is fixed, as are the departure/arrival times for each route. In the model, airport opening is considered an active state, and closure is considered an inactive state, allowing flights to re-enter routes. Taking into account factors such as weather, departure/arrival capacity, etc., the following constraints can be derived:

\( \sum _{a∈A,h∈H_{F}^{D}:U=b,t∈O}x_{h}^{a}(t)≤P_{dep,b}^{n}∀b∈B,n∈N \)	(5)
\( \sum _{a∈A,h∈H_{F}^{D}:V=b,t+W∈O,i∈I}x_{h}^{a}≤P_{arr,b}^{n}∀b∈B,n∈N \)	(6)
\( \sum _{a∈A,h∈H_{F}^{D}:U=b,t∈O}x_{h}^{a}(t)+\sum _{a∈A,h∈H_{F}^{D}:V=b,t+W∈O,i∈I}x_{h}^{a}≤P_{gen,b}^{n}∀b∈B,n∈N \)	(7)
\( \sum _{a∈A,h∈H_{F}^{D},i∈[2,I-1]:J=g,t+W∈O,i∈I}x_{h}^{a}(t)≤P_{ent,b}^{n}∀g∈G,n∈N \)	(8)
\( \sum _{h∈H_{F}^{D},t∈T}x_{h}^{a}(t)=1∀a∈A \)	(9)
\( x_{h}^{a}(t)∈\lbrace 0,1\rbrace ∀a∈A,h∈H_{F}^{D},t∈T \)	(10)

Equations (5)-(7) respectively enforce the departure, arrival, and total capacity constraints for the airport. The total number of flights at the airport includes both departure and arrival flights, and the airport capacity constraint is defined by Equation (8). Equations (9) and (10), under the condition that the decision variable\( x_{h}^{a}(t) \)is binary, mandate each flight to select a single departure time and route.

4.Model Instance Verification

4.1.Data Acquisition

Air traffic data for flights from Shuangliu Airport to Tuofeng Airport and flights from Shuangliu Airport to Mangshi Airport were collected, including flight information, routes, departure/arrival times, various operational costs, departure/destination airport weather information, alternative routes, airport capacities, routes, aircraft types, and airline types. The historical data mentioned above were obtained by consulting relevant websites and materials from the Civil Aviation Administration of China, Southwest Air Traffic Management Bureau, Yunnan Air Traffic Management Sub-Bureau, Shuangliu Airport, Tuofeng Airport, and Mangshi Airport, among others. Some of the data are presented in Table 2.

Table 2. Data Collection

Departure Airport	Destination Airport	Departure Time	Arrival Time	Destination Airport Hourly Capacity
Shuangliu Airport	Tuofeng Airport	18:40	20:30	9
Shuangliu Airport	Mangshi Airport	21:10	23:00	16

This paper estimates the operational strategic cost for each flight, using the maximum takeoff weight as the classification criterion. The description of routes and departure times is based on clustering flight data from Shuangliu Airport to Tuofeng Airport and Shuangliu Airport to Mangshi Airport during the months of June to September each year. It determines three groups of available route sets for each OD pair-aircraft type, allowing takeoff times 30 minutes before and after the originally scheduled departure time. The description of route toll costs is based on the Civil Aviation Administration’s settlement center and relevant regulatory documents, as shown in Table 3.

Table 3. Civil Aviation Administration’s Route Toll Standards

Aircraft Type	Cost per Kilometer (CNY)	Cost per Flight Hour (CNY)
Boeing 747-400 (Full Pax)	202	174528
Boeing 747-400CMBI	148	127872
Boeing 747-200CMBI	135	116640
Boeing 747-SP	135	116640
Boeing 767-300	113	93564
Boeing 767-200	104	86112
Boeing 757	95	66868
Boeing 707	73	54604
Boeing 737-300	66	44676
Boeing 737-200	61	39420
Boeing 737-500	63	42048
Airbus 300	130	96214
Airbus 310-300	96	69350
Airbus 310-200	108	75628
McDonnell Douglas MD-11	160	133298
McDonnell Douglas MD-82	70	47158
BAE 146-100	45	26426
BAE 146-300	56	38080
Ilyushin Il-8	30	12147
Antonov An-24	25	8978
Yun-7	25	8978
Yun-12	10	2146
Shorts 360	19	6832
SAAB-340	20	9200

The selection of departure and arrival times during the rainy and foggy period from June to September is strategic. During this period, both Tuofeng Airport and Mangshi Airport face weather restrictions on their capacities. However, the capacity limitation at Mangshi Airport is smaller than that at Tuofeng Airport. Choosing to fly to Mangshi Airport during the same time frame for the same flight is more economical and results in lower operational costs, providing decision criteria for allocating strategic flight plans in the model.

To better illustrate the variation in airport capacity with changing weather conditions, and despite the simultaneous reduction in capacity at both Tengchong and Mangshi airports, the capacity of Mangshi Airport is larger than that of Tuofeng Airport. This paper presents the flight statistics for direct flights from Shuangliu Airport to Tuofeng Airport and from Shuangliu Airport to Mangshi Airport for the months of June to September in 2020, as shown in the following figure.

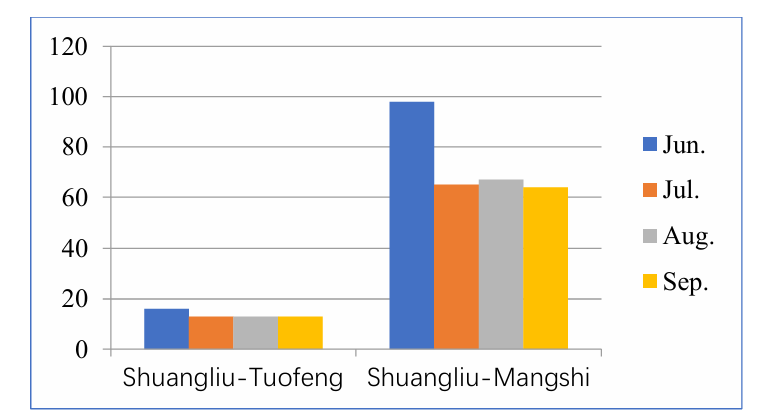
Figure 3. A Comparison of Flight Volumes from Chengdu to Tengchong and Chengdu to Mangshi Airports in June-September 2020

4.2.Results and Analysis

By solving the model, two scenarios, FMS1 and FMC1, were compared. Although they share the same variables and constraints, the difference in the objective functions led to variations in the solution results. In terms of flight replacements, as indicated by the data in Tables 4 and 5, it is evident that FMS1 has the fewest replaced flights, while FMC1 has more than twice the number of replaced flights compared to FMS1.

Taking flights from Chengdu Airport directly to Tuofeng Airport as an example, where the hourly capacity of Tuofeng Airport is 9, actual weather conditions may reduce the airport’s capacity to below 9. However, the number of flights remains at 9, leading to a situation of demand exceeding capacity, resulting in flight delays or cancellations. In contrast, Mangshi Airport is less affected by weather, and although its airport capacity is lower than 16, it is still higher than 9. This provides a prioritized solution for adjusting the flight schedule from Chengdu Airport directly to Tuofeng Airport to the flight schedule from Chengdu Airport directly to Mangshi Airport. In both the FMS1 and FMC1 scenarios, most flights require only minor departure or arrival replacements, with few significant changes. To balance airport capacity, timely replacements are necessary for some flights. This replacement is not only a part of the model’s decision but also involves the reselection of routes. Meanwhile, considering the simulated hourly capacity of Tuofeng Airport/Mangshi Airport as 9/16, the route selection only leads to a small number of departure and arrival replacements for a few flights, resulting in a relatively minor overall impact on the strategic flight plan.

Table 4. Number of Replaced Flights for Departure and Arrival

	Replaced Flights	Departure Replacement Flights (minutes/flight)	Arrival Replacement Flights (minutes/flight)	Departure Replacement Flights (minutes/flight)	Arrival Replacement Flights (minutes/flight)
Original Submission Plan	187	N/A	3.11	N/A	0.11
MS1	365	4.97	4.97	0.18	0.18
MC1	931	4.74	4.85	0.24	0.25

In terms of flight operational costs, an analysis of various costs under different scenarios was conducted based on the data in Table 4. The results indicate that while the costs for aircraft and fuel are nearly identical across different scenarios, there are variations in average route costs. Flight operational costs represent the average cost of flights displaced in space or time, i.e., these flights will have different strategic flight plans. In the comparison between the FMS1 and FMC1 scenarios, the total cost of FMS1 is lower than that of FMC1, indicating that the strategic flight plans allocated by FMS1 are more optimized in terms of cost. The model results lean towards replacing flights originally from Chengdu Shuangliu International Airport to Tuofeng Airport with flights from Chengdu Shuangliu International Airport to Mangshi Airport, thus achieving cost savings. To assess the changes in costs more accurately, we introduced the standard deviation formula to represent the precision of the cost set. The calculation of the standard deviation can help us understand the range and reliability of cost data. The specific standard deviation formula is as follows:

\( σ=\sqrt[]{\frac{1}{N}\sum _{v=1}^{N}({x_{v}}-μ{)^{2}}} \)

(11)

Where,\( N \)is the number of samples,\( {x_{v}} \)represents the specific value of each sample,\( μ \)is the mean, and\( σ \)is the standard deviation.

Table 5. Average Strategic Cost Items

	Original Submission Plan	FMS1	FMC1
Airside Cost (CNY)	21789.74	21789.45	21789.57
Fuel Cost (CNY)	28418.11	28416.75	28418.14
Landside Cost (CNY)	N/A	2899	3051
Route Cost (CNY)	3218.67	3299.39	3224.64
Total Cost (CNY)	53426.52	56404.59	56483.35
Standard Deviation\( σ \)	12032.70	11249.14	11230.16

Based on the above results, the model adjusts the flight schedules originally designated for direct flights from Shuangliu Airport to Tuofeng Airport to now be directed to Mangshi Airport. This adjustment ensures that the results fall within 9/16 of the simulated airport hourly capacity. Compared to resolving this issue through tactical means, employing strategic measures to adjust the strategic flight plan provides airlines and flight crews with more suitable flight schedules. This approach avoids solving the imbalance between traffic demand and capacity by resorting to flight delays or cancellations on the day of operation. In terms of flight utilization, the adjusted flight plan still accomplishes the mission without wasting flight resources. In operational costs, adhering to the adjusted schedule reduces subsequent costs for airlines, such as expenses for passenger meals and accommodation, saving on fuel, airport usage fees, and route charges. Regarding airline services, it promotes the operational efficiency of airlines and airports, ensures the timely travel rights of passengers, and enhances the corporate image of both airlines and airports.

5.Conclusion

This study addresses a critical challenge currently faced by the aviation industry— the imbalance between airport capacity constraints and the increasing demand for flights. An innovative integer programming model aimed at efficiently formulating strategic flight plans is proposed. Through empirical research focused on the rainy and foggy season from June to September, the study confirms the feasibility of adjusting flight schedules from Chengdu Shuangliu International Airport directly to Tuofeng Airport to instead fly directly to Mangshi Airport. This adjustment not only effectively reduces the risk of flight delays or cancellations but also lowers operational costs for airlines and airports, demonstrating the practicality and value of the model.

However, the model in this study has certain limitations. Firstly, it primarily focuses on airport capacity constraints and does not adequately consider restrictions related to route and sector capacity. Secondly, data collection is predominantly concentrated on the months of June to September, failing to comprehensively cover various seasons and diverse weather conditions throughout the entire year. Additionally, the implementation of policy support and coordination mechanisms for adjusting strategic flight plans still needs improvement, potentially affecting the widespread application and practical effectiveness of the model.

Future research efforts will be dedicated to addressing these limitations. Specifically, the model will be expanded to incorporate constraints related to route and sector capacity, thereby providing more comprehensive flight plan optimization solutions. Furthermore, extensive data collection and analysis will be conducted to ensure the model’s applicability and accuracy across different seasons and varied weather conditions. Simultaneously, exploration will be undertaken to identify more effective policy support and coordination mechanisms to facilitate the seamless implementation of strategic flight plans. These anticipated improvements aim to enhance the model’s computational efficiency and precision, providing the aviation transportation industry with a more efficient and reliable decision support tool.

Funding

Key Technology Research and Verification of Air-Ground Integration for Small and Medium Airport Clusters (U233320025); Research on Airport Cluster Collaborative Effects and Dynamic Collaborative Development Mechanism Based on Spatiotemporal Network Characteristics of Air-Ground Traffic Systems (23JCYBJC00050)

References

[1]. LI Chenlin, SUN Zhiping, FAN Pengcheng, et al. On the Optimal Allocation of Flights and Gates for Airports with Newly-builtSatellite Hall [J]. China Transportation Review, 2019, 41(09):27-32+49.

[2]. Zhao Shupeng. Research on flight-gate allocation optimization problem based on greedy algorithm[J]. Intelligent City, 2020, 6(04):130-131.

[3]. DING H, LIM A, RODRIGUES B, et al. The over-constrained airport gate assignment problem[J]. Computers & Operations Research, 2005, 32(7):1867-1880.

[4]. ZHANG Yunpeng, MU Yao. Study on Optimization Model of Departure Flight Scheduling in Multi-runway Airports [J].Journal of Civil Aviation Flight University of China, 2023, 34(05):5-9+15.

[5]. Wei-Wei Chen, Rui Geng, De-Guang Cui. Optimization of sequencing and scheduling for arrival flights in the approach area [J]. Journal of Tsinghua University(Science and Technology, 2006, (01):157-160.

[6]. Li, Keyang. Establishment and Simulation of Ground Waiting Model Based on Flight Timing Optimization [J]. Modern Computer, 2023, 29(01):50-53+73.

[7]. ZHANG Yuzhou, ZHANG Ziwei, JIANG Keqin. Modeling and Co-optimization of Multi-Runway arrival-departure ground-holding Problem modeling and collaborative optimization[J]. Journal of Nanjing University (Natural Science), 2020, 56(01):132-141.

[8]. Xiang Zheng, He De Yong, Gao Hua, et al. Comparative study of centralized processing of flight plans in China and Europe[J]. China Science and Technology Information, 2019, (11):35-37.

[9]. KAMMOUN MOHAMED ALI S A, REZG NIDHAL, . A Flight Plan Rescheduling in Air Traffic Management Problem: A Time Discret Event System Approach[J], 2012, 45(6):285-290.

[10]. JACQUILLAT A, ODONI A R. An Integrated Scheduling and Operations Approach to Airport Congestion Mitigation[J]. Operations Research, 2015, 63(6):1390-1410.

[11]. Chen Fenglan. Research on the influence of the relationship between military aviation activities and route location on sector capacity[J]. Technology Innovation and Application, 2016, (23):81-82.

[12]. BOLIĆ T, CASTELLI L, COROLLI L, et al. Reducing ATFM delays through strategic flight planning[J]. Transportation Research Part E: Logistics and Transportation Review, 2017, 98:42-59.

[13]. STARITA S, STRAUSS A K, FEI X, et al. Air Traffic Control Capacity Planning Under Demand and Capacity Provision Uncertainty[J]. Transportation Science, 2020, 54(4):882-896.

[14]. XU Y, PRATS X, DELAHAYE D. Synchronised demand-capacity balancing in collaborative air traffic flow management[J]. Transportation Research Part C: Emerging Technologies, 2020, 114:359-376.

[15]. KICINGER R, CHEN J-T, STEINER M, et al. Airport Capacity Prediction with Explicit Consideration of Weather Forecast Uncertainty[J]. Journal of Air Transportation, 2016, 24(1):18-28.

[16]. Zhang Jing. Research on airport capacity and delay assessment of weather impact [D]. 2012.

[17]. YU Wei, SHAO Tsuen, XIANG Hongyi, et al. Research on lmpact of Bad Weather Based on Complex Network on Flight Delay [J]. Aeronautical Computing Technique 2018, 48(02):48-51+56.

[18]. Wang N, Yang H R, Zhou J J, et al. Quantitative study on the impact of severe weather on departure flight delays at Urumqi Airport[C]. The 35th Annual Meeting of the Chinese Meteorological Society, 2018:12.

[19]. Li Yinfeng. Research on key technology of airspace resource allocation in complex airport terminal area [D]. 2015.

Cite this article

Ye,Z.;Pang,Q.;Hu,L. (2024). Strategic flight planning models based on integer programming: Optimizing air traffic and airport capacity. Applied and Computational Engineering,65,210-221.

Data availability

The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.

Disclaimer/Publisher's Note

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

About volume

Volume title: Proceedings of Urban Intelligence: Machine Learning in Smart City Solutions - CONFSEML 2024

ISBN：978-1-83558-427-9(Print) / 978-1-83558-428-6(Online)

Editor：Omar Marwan

Conference website: https://www.confmss.org/

Conference date: 2 February 2024

Series: Applied and Computational Engineering

Volume number: Vol.65

ISSN：2755-2721(Print) / 2755-273X(Online)

© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license. Authors who publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See Open access policy for details).