1. Introduction

In real-time strategy games, players' decisions critically shape the game's outcome, with each choice impacting their probability of success [1]. Players strive to identify the most effective strategy to optimize their chances of winning, yet often rely solely on personal experience for decision-making. Incorporating algorithms that make optimal choices can significantly enhance a player's likelihood of winning and deepen their understanding of various strategies.

The multi-armed bandit (MAB) problem, addressing the exploration-versus-exploitation dilemma, offers a robust method for finding a balance between these two strategies. The core focus of MAB is determining the operational approach that maximizes cumulative rewards [2]. MAB algorithms have found applications in diverse fields such as online marketing, medical trials, and website design, proving effective in scenarios that require dynamic decision-making. In online marketing, for instance, they assist in optimizing ad placement to enhance user click-through rates. Real-time strategy games share parallels with such models [3], where the primary objective is to maximize rewards and ultimately secure a victory, necessitating a balanced approach to exploration and exploitation. Moreover, the advent of game updates and downloadable content has facilitated the dynamic alteration of strategies, a significant shift from past gaming practices.

This paper focuses on applying MAB algorithms to decision-making in real-time strategy games, specifically using Space Craft as the experimental platform [4]. In Space Craft, players continuously make decisions affecting the final outcome. Given the game's complexity, the study concentrates on the initial series of decisions to construct a simplified model. Classic MAB algorithms, including Explore-Then-Commit (ETC), Upper Confidence Bound (UCB), and Thompson Sampling, are applied to this context. The algorithms' effectiveness is assessed through simulations yielding a dataset reflective of the game's potential outcomes [5]. The key performance indicator employed is cumulative regret, an essential metric for evaluating an algorithm's superiority. Through comparative analysis, the study aims to ascertain the most suitable algorithm for decision-making in real-time strategy games.

2. Theoretical Foundations

2.1. Defining Multi-Armed Bandit

At every stage of behavior and decision-making, from animals to human, there is a need to strike a balance between exploration and exploitation [6]. And the key of the multi-armed bandit problems is the balance between exploration and exploitation. There are several muti-armed bandit algorithms, such as \( \varepsilon \) -greedy algorithm, Explore-Then-Commit (ETC) algorithm, Upper Confidence Bound (UCB) algorithm and Tompson Sampling and so on.

The first algorithm that will be introduced in this passage is ETC algorithm, which commits to the arm that showed the best during exploration and then explores by playing each arm a set number of times. The number of times ETC examines each arm, represented by a natural number m, is what defines it. The algorithm will search for mk rounds due to the k actions, and then select one action for each of the next k rounds [7].

Let \( \mu_i \) (t) be the average reward received from arm I after round t, which is \( \mu_i(t)=\frac{1}{T_i(t)}\sum_{s=1}^{t}{I\ {A_s=i}\ X_s} \) , where \( T_i(t)=\sum_{s=1}^{t}{I\ {A_s=i}\ } \) is the number of times action I has been played after round t. What’s more, the mean rewards of action \( \mu_1,...{,\mu}_k\ \) are unknown. The goal of this algorithm is to maximize total reward and minimize the cumulative regret.

The cumulative regret of ETC is written as \( R_n=\sum_{i=1}^{k} ∆_{i} E[T_{i}(n)] \) , where \( ∆_{i}=μ^{∗} - μ_{i} \) and \( \mu^\ast=max\ \mu_i \) .

The core of ETC algorithm is to explore by playing each arm a fixed number of times and then exploits by committing to the arm that appeared the best during exploration. Epsilon-greedy, or \( \varepsilon \) -greedy, is a popular ETC algorithm that chooses an arm by choosing a random arm \( \varepsilon \) % of the time and being greedy and choosing the best arm (1- \( \varepsilon \) )% of the time. This algorithm is simple to use and doesn’t require any previous understanding of the reward distributions. One of the difficulties is that the algorithm will continue to choose at random \( \varepsilon \) % of the time regardless of whether it converges to the optimal result. Although there are methods to cause \( \varepsilon\ to \) deteriorate with time, they are not employed in this passage [8].

The next algorithm to be discussed is Upper Confidence Bound (UCB) algorithm. UCB algorithm has some advantages over ETC algorithm. It behaves better when there are more than two arms and it doesn’t depend on advance knowledge of the suboptimality gaps [9]. The optimism principle, according to bandits, involves employing the data that has been observed thus far to assign a value-known as the upper confidence bound to each arm that is most likely an overestimation of the unknown mean. The core idea of UCB is to assign an upper confidence bound to each action and select the action with the highest bound. The UCB formula is given by: \( a_t=argmax({\bar{x}}_a+\sqrt{\frac{2\ ln\ t}{n_a}\ } \) ), where \( a_t \) is the action selected at time t, \( {\bar{x}}_a \) is the average reward of action a, \( n_a \) is the number of times action a has been selected and t is the current time step.

The first component of the formula, \( {\bar{x}}_a,\ \) stands for exploitation, or the selection of courses of action that have historically yielded positive results. The second component \( ,\sqrt{\frac{2\ ln\ t}{n_a}\ } \) , stands for exploration; it encourages exploration by providing a greater upper confidence level for actions that haven’t been tried as often. The formula for cumulative regret is \( R_T=\sum_{t=1}^{T}\left(x^\ast - x_{a_t}\right), \) where \( R_T \) is the cumulative regret at time T, \( x^\ast \) is the expected reward of the best action, \( x_{a_t} \) is the expected reward of the action chosen by the algorithm at time t, and T is the total number of time steps.

And the last algorithm talking in this passage is Tompson Sampling, which is also known as Bayesian Bandits. The core idea of Tompson Sampling is to keep a probability distribution for reward linked to every action, which reflects our perception of how well the action was performed. These distributions change when more information is obtained by carrying out activities and observing their results. The algorithm selects the action with the greatest sampled value by taking samples from various distributions before making a decision [10]. The exploration and exploitation process are naturally balanced: actions with wider distributions and higher levels of uncertainty are more likely to be examined, while actions with higher expected rewards are more likely to be exploited.

The process of Tompson Sampling algorithm is as follows: it begins by initializing a probability distribution for each action, usually a Beta distribution with parameters \( \alpha=1\ and\ \beta=1 \) , which express our initial estimation of how likely each action is to succeed. The first step is to sample a value from its Beta distribution and then choose the action with the highest sampled value. Next step is to observe the reward for the selected action, which is usually 1 for success and 0 for failure. Last step is to update the Beta distribution for the selected action based on the observed reward.

Tompson sampling adjusts its exploration-exploitation technique in an effort to maximize the process of making decisions over time by iteratively updating the probability distributions in response to observed rewards.

2.2. Comparative Analysis of Algorithms

In this part, the performances of different algorithms are showed through testing them with the same dataset. Cumulative regret is the index that is used to evaluate the performance.

These three algorithms, ETC, UCB and TS are tested with the same dataset and the same horizon. It can be found that different algorithms show different performance when horizon n is different.

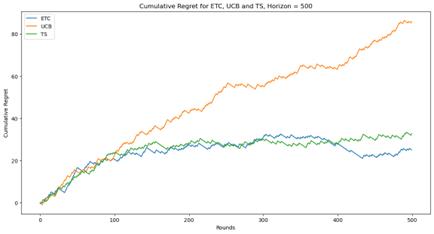
(a)

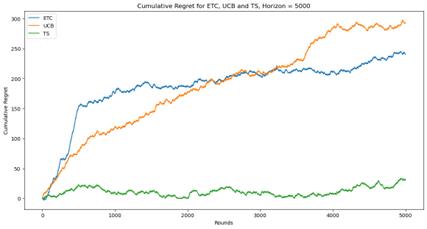
(b)

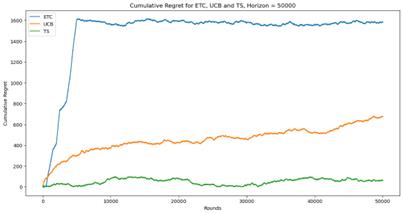
(c)

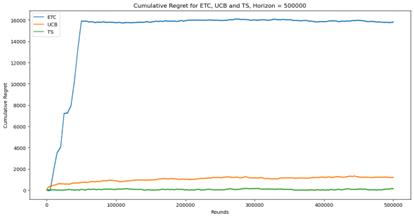
(d)

Figure 1. Cumulative regret for ETC, UCB and TS (Photo/Picture credit: Original).

As shown in Figure 1, When n=5000, the TS algorithm shows a logarithmic behavior. When n=50000, the UCB algorithm shows a logarithmic behavior. When the value of n is low, none of these three algorithms has a clear advantage. But when n is large enough, the TS algorithm is obviously better. The ETC algorithm shows great effectiveness when n is small, but when n increases, the effect becomes very poor.

Actually, these three algorithms have their own advantages and disadvantages. ETC algorithm is the simplest way to handle the problem of the balance between exploration and exploitation. But the length of the stage of exploration needs to be known before using this algorithm, which is hard to realize in the practical application. When entering the stage of committing, ETC algorithm will stop explore new actions, which may miss a better choice. UCB and TS algorithm can solve this disadvantage easily. They can adjust the proportion of exploration and exploitation dynamically according to the practical situation. But the cost of calculation and storage will increase dramatically and the time to run the algorithm will increase too. The difference between UCB and TS algorithm is that UCB is calculating the upper confidence bound to balance exploration and exploitation while TS is using the probabilistic model. Thus, they are suitable for different situations.

2.3. Broad Applications

Recently, multi-armed bandit (MAB) framework has garnered significant interest in a number of applications in recent years, including recommender systems and information retrieval to healthcare and finance, as a result of its exceptional performance paired with a few desirable characteristics, like learning with less feedback.

The first application is healthcare. In clinical trials, MAB algorithms are used to design adaptive allocation strategies to improve the efficiency of data collection. This method uses exploration and exploitation between different treatment options to find the most promising treatment options. For instance, using the MAB algorithm can gradually allocate more samples to a well-performing treatment over the course of a trial, while reducing investment in a poorly performing treatment. What’s more, with the MAB algorithm, doctors can find the most appropriate initial dose for each patient, thereby reducing the risk of adverse reactions.

Next comes the application in the financial sector. The MAB algorithm is used for online portfolio selection to maximize cumulative rewards by exploring the exploiting across multiple assets. While in practical application, it is possible to use the MAB algorithm to construct an orthogonal portfolio based on a risk-adjusted return function to derive the best portfolio strategy that combines passive and active investing.

What’s more, the MAB algorithm is used tin the dynamic pricing problem of online retailers to determine the real-time price of a product by making a trade-off between immediate profit and future profit learning. The MAB algorithm is also used to solve the exploration-exploitation dilemma in recommendation systems, that is, the need to explore new items that the user may be interested in while exploiting known user preferences.

3. Applications in Real-Time Strategy Games

3.1. Game Theory Context

One of the most played real-time strategy games in history is StarCraft. When Blizzard Entertainment released it in 1998, it sold an astounding 9.5 million copies. A major factor in the game’s success was its competitiveness. Over the years, hundreds of events attracted thousands of professional players.

In StarCraft, there are three different playable races: Protoss, Zerg, an Terran. The Protoss represent a highly developed and sentient species of alien humanoids. A race of aliens known as the Zerg go for genetic perfection. Finally, the Terrans are the near future humanity. StarCraft is known for its competitive balance. Every race has its own strengths and weakness so players have to use suitable strategies in the game.

Destroying the opponent's base is the aim of the game. Each player must construct his own base, gather resources, train units, and deploy the army to both attack and defend his base against opponent attacks in order to do this. Each unit can be given a variety of instructions, including attack, hold position, move, and attack move.

Since the model of this whole game is too complicated to analyze, a strategy called Overkill is taken as an example. It is a situation that happen at the beginning of a game. In this situation, players have to choose between three deployment strategies. They are welveHatchMuta, TenHatchMuta, and NinePoolling, which are replaced by strategy A, strategy B, strategy C since it looks simpler and easier to understand.

3.2. Algorithm Implementation

The arms are these three different strategies they are TwelveHatchMuta, TenHatchMuta, and NinePoolling. And the result is win or lose. It is used in the algorithm that 1 for win and 0 for lose. The bot will decide which strategy to take next time according to the result of last n games.

Since the strategies in the game needs to be adjusted and changed in real time, ETC algorithm can not achieve the requirement. So UCB algorithm and TS algorithm are chosen to be implemented in the test.

The first one is Upper Confidence Bound algorithm, in the algorithm, winning rate of each strategy (which can also be called arm) are unknown. Therefore, the method of generating random number is used here to simulate the winning rate of each strategy. Although this method may not be very accurate at the beginning, when the dataset is large enough, it can still simulate the real situation in the game. Random seed is used for reproducibility of results. Next, the outcome of a trail for a given strategy is simulated. 1(success) or 0(failure) are returned based on the true success rate of the strategy. The next step is the core of the entire algorithm implementation. The UCB algorithm is used to calculate the upper confidence bound value of each strategy, and make a choice to balance exploration an exploitation. Next, the algorithm chooses the strategy with the largest UCB value and calculate the rewards. The computation of cumulative regret, or the difference between the total reward that might have been gained by consistently selecting the best strategy and the total reward that was actually obtained, is the last step in the algorithm's calculation.

Next one is the Tompson Sampling algorithm. Their simulation environment is the same, but the core algorithm is different. For each strategy, there are two main parameters, ‘alpha’ and ‘beta’, which represent the number of success and failures respectively. Firstly, the algorithm samples a value from the Beta distribution for each strategy. Then the strategy with the highest sampled value will be chosen, and the outcome of the chosen strategy will be stimulated. Lastly, the corresponding ‘alpha ’and ‘beta’ is updated and the cumulative regret will be calculated too.

3.3. Results Analysis

Three distinct arms are chosen for the experiment, and there are 1000000 rounds total. They are tested using the UCB and TS algorithms, respectively, and their cumulative regret values are calculated. The Figure 2 depicted the curve of their cumulative regret values changing with the number of rounds.

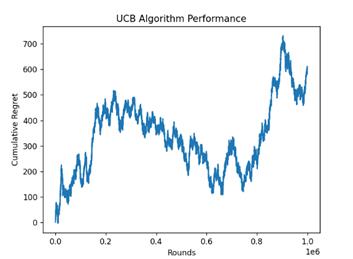
(a)

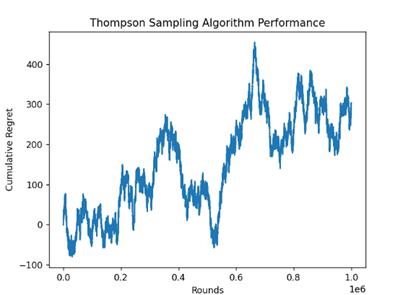
(b)

Figure 2. Performance of UCB and TS algorithm (Photo/Picture credit: Original).

It is common to observe that when the number of experimental rounds rises in both graphs, the cumulative regret value of both algorithms increases. The cumulative value of the loss incurred by choosing the less-than-optimal option in comparison to the ideal choice is represented by the cumulative regret index, which is frequently used to assess how well a multi-arm bandit algorithm is performing.

The cumulative regret of UCB algorithm showed an overall upward trend, but there is a large fluctuation in the late stage of the experiment, which may indicate that the UCB algorithm faces some challenges in determining how to choose the best arm, especially in the case of non-stationary or complex reward distributions.

The cumulative regret of TS algorithm also increase rapidly in the initial stage of the experiment, and then the growth slows down, which indicates that the algorithm learns quickly and approaches the optimal strategy. On the whole, the cumulative regret fluctuate within a certain range, but there is no significant upward trend, indicating that the TS algorithm has a good balance between exploration and exploitation.

3.4. Algorithm Enhancement

There are other algorithms that can handle this problem of real-time strategy games, and contextual algorithms may be one of them. In each round, the algorithm first observes the current context information, then selects a strategy (or action) based on this information, and then receives a reward associated with the chosen strategy. The goal of the algorithm is to maximize long-term rewards, which is usually achieved by learning the relationship between contextual information and strategic rewards.

Reinforcement learning or neural networks can be used to determine the corresponding context model, and after learning from large amounts of data, the model will become more accurate and the results will be better.

4. Challenges and Future Prospects

The first challenge in real-time strategy games is the uncertainty of the reward, because the player does not know the reward when making a strategy choice, that is whether the strategy choice will lead to win or lose.

In addition, the player’s choice is also particularly random, because each opponent’s preferences are different, so the choice of strategy is also different. This will definitely increase the difficulty of the algorithm operation.

Since the application of muti-armed bandits on real-time strategy games is a new topic, there are still lots of avenues for further research. Research in this area is definitely valuable, not only for improving the winning rate of ordinary players, but also for training professional players, or for game developers to design more powerful Non-Player-Characters.

5. Conclusion

The findings regarding cumulative regret values indicate that employing UCB and TS algorithms can significantly diminish cumulative regret, thereby enhancing players' win rates in games like StarCraft. This application is not only effective in StarCraft but also holds potential for extension to other real-time strategy games and more complex scenarios. Multi-armed bandits effectively assist players in selecting the optimal strategy, maintaining a delicate balance between exploration and exploitation. The application of multi-armed bandit algorithms in this context is particularly intriguing, as it represents a largely uncharted area of exploration. In fields with more established applications, such as recommendation systems and clinical medicine, even minor algorithmic optimizations can yield substantial benefits. In this novel field, every discovery and achievement carries substantial value and potential for impact. Although certain aspects of this research remain to be refined, future investigations promise to deepen understanding and uncover more findings in this area. Concurrently, the development and implementation of more sophisticated and effective code models is anticipated, further advancing this field of study.