1. Introduction

In the evolving landscape of the cinematic domain, the role of movie recommendation systems has grown profoundly. Amidst the digital age, individuals face an overwhelming amount of information online, making it increasingly challenging to discern and identify content tailored to personal preferences [1]. This challenge becomes even more evident in the realm of cinematography, where discerning aficionados seek titles aligned with their tastes from an ever-growing array of choices [2]. Such a scenario underscores the need for an adept recommendation system. When effectively employed, such systems not only satiate individual cinematic inclinations but also augment the commercial value of platforms that harness these algorithms [3].

While the academic canvas is adorned with a myriad of notable studies on the subject, there's a pressing need to critically reassess the methodologies steering movie recommendation systems. Among the prevalent methods, we identify three broad categories: The Demographics-Based Recommendation Algorithm, the Content-Based Recommendation Algorithm, and both User-Based and Item-Based Collaborative Filtering. These methods have their unique characteristics and applications [4].

This paper seeks to shed light on these methods, particularly homing in on the comparative nuances of Enhanced KNN-based Techniques in movie recommendations. A significant contribution of this work is the introduction of a novel approach named Hybrid User-Movie KNN, which synergizes user KNN and movie KNN, offering a refined perspective in the field. By undertaking a meticulous exploration, we endeavor to propose incremental refinements to the existing landscape, thereby enriching both the theoretical paradigms and their pragmatic applications.

The discourse is systematically segmented into five distinct sections. Post this introduction, the second section embarks on a journey through the annals of seminal literature, furnishing insights into antecedent studies on recommendation algorithms. The third section delves deep into the intricacies of Enhanced KNN-based Techniques, including the Hybrid User-Movie KNN, exploring their potential and implications. The fourth section offers a critical vantage point, dissecting the advantages and potential pitfalls of these techniques or their contextual application. Concluding the narrative, the fifth section encapsulates the overarching themes, accentuating the inherent constraints of our exploration while charting the trajectory for impending scholarly pursuits.

2. Literature Review

2.1. Recommendation system

In the realm of recommendation systems, various methodologies have been explored and developed. Herlocker, et al. [5] investigated collaborative filtering, emphasizing the importance of neighborhood size and similarity metrics. Pazzani and Billsus [6] focused on content-based recommendation systems, discussing feature selection methods and similarity measures. Burke [7] presented hybrid models, combining collaborative filtering and content-based methods, and highlighted their advantages. Zhang, et al. [8] provided an extensive overview of deep learning techniques, emphasizing the potential of deep learning in capturing complex patterns. Adomavicius and Tuzhilin [9] explored challenges and future directions in personalized recommendation, considering various contextual factors such as time, location, and social connections.

The literature on recommendation systems underscores the multifaceted nature of this field, encompassing collaborative filtering, content-based methods, hybrid models, deep learning, and personalized recommendation. The selected studies contribute to a foundational understanding of the current landscape, revealing the complexity and potential of various approaches. The ongoing evolution of these methodologies offers rich opportunities for research and innovation, pointing to exciting avenues for future exploration and development in recommendation systems.

2.2. KNN algorithm

The K-Nearest Neighbors (KNN) algorithm has been a foundational technique in various domains, including recommendation systems, classification, and regression. Sarwar, et al. [10] applied KNN in collaborative filtering for recommendation systems, demonstrating its effectiveness in predicting user preferences based on similarity measures. The authors emphasized the importance of selecting appropriate distance metrics and neighborhood sizes to enhance recommendation accuracy. Desrosiers and Karypis [11] extended the KNN algorithm by introducing item-based collaborative filtering. They highlighted the benefits of item-based approaches over traditional user-based methods, particularly in handling sparse data and scalability issues. The study provided insights into the adaptability of the KNN algorithm in different collaborative filtering paradigms. In the context of hybrid models, Park and Pennock [12] integrated KNN with matrix factorization techniques to create a more robust recommendation system. The authors showed that the combination of KNN with other algorithms could overcome some inherent limitations of KNN, such as sensitivity to noisy data. He, et al. [13] proposed a novel approach to enhance the KNN algorithm by incorporating implicit feedback and localized item-item models. Zhang, et al. [14] explored the application of the KNN algorithm in content-based recommendation systems.

The literature on the KNN algorithm illustrates its wide applicability and adaptability in various recommendation contexts. From collaborative filtering to hybrid models and content-based recommendations, the KNN algorithm continues to be a vital tool, with ongoing research enhancing its efficiency, scalability, and accuracy. The selected studies contribute to a comprehensive understanding of the KNN algorithm's role in recommendation systems, revealing its multifaceted applications and potential for future innovation.

3. Research methods

3.1. Research design

The first is to collect Movie data. This experiment uses the movie data in The Movie Database (TMDB). The collaborative filtering model and SVD model are used in this project. The experimental results were verified by 5-fold cross-checking.

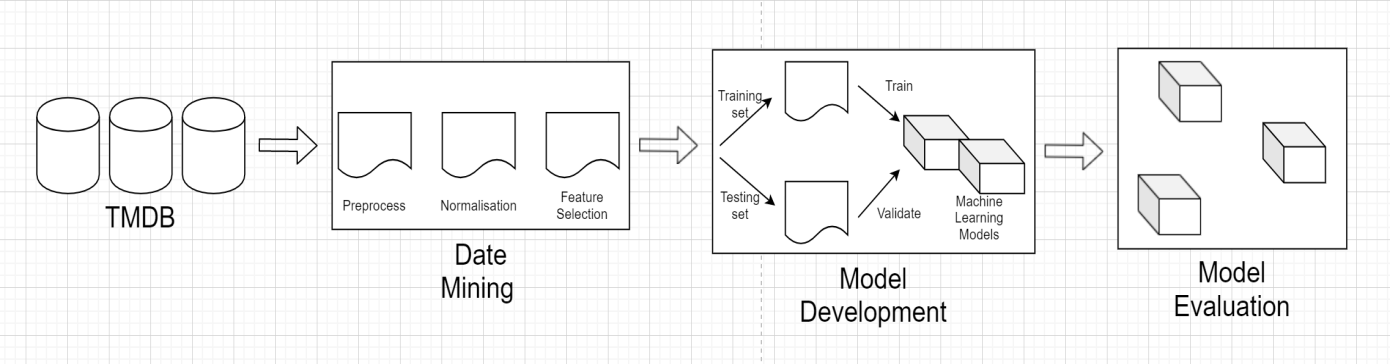
Figure 1. The progress of machine learning.

3.2. Data collection

As shown in Figure 1, firstly, an account was registered on the TMDB website, and a request for an API key was submitted. To obtain the key, the "Settings" section was navigated to, followed by the "API" tab, where the instructions for key creation were duly followed. This key subsequently facilitated access to the TMDB API by enabling the transmission of HTTP requests.

Data Cleaning: An essential preliminary step involved the cleansing of the data. Missing values and anomalies were addressed using the delete method, ensuring the integrity and consistency of the data set.

Data Preprocessing: In addition to the existing data, supplementary information pertaining to the movies was incorporated. This augmentation included details such as the release date, rating, popularity, and other relevant attributes. A carefully structured division of the user rating matrix was then implemented for the training and testing phases. Specifically, 85% of the matrix was allocated for training, while the remaining 15% was designated for testing. The partitioning strategy employed was systematic: for each user's rating of a particular movie, a random number was generated. If the value exceeded 0.85, the data was assigned to the test set. Conversely, if the value was less than or equal to 0.85, the data was allocated to the training set.

3.3. Model selection

3.3.1. KNNBasic. KNNBasic, or K-Nearest Neighbors Basic, is a non-parametric method utilized in classification and regression tasks. It operates on the principle of feature similarity, identifying the k closest training examples to a given input and making predictions based on the majority class among these neighbors or the mean value in the case of regression [15].

The algorithm consists of the following key components:

• Number of Neighbors (k): A predefined number of nearest neighbors to be considered for predictions.

• Distance Metric: A measure such as Euclidean or Manhattan distance to quantify the similarity between instances.

• Prediction Rule: For classification, a majority vote among the k neighbors is used, while for regression, the mean value may be employed.

• Optional Weighting Scheme: Neighbors may be weighted based on their distance to the query point, giving closer instances more influence on the prediction.

KNNBasic is known for its simplicity and ease of implementation but can be computationally demanding due to the need to compute distances between all pairs of instances. Its application spans various domains, including recommendation systems, where it can be employed in both user-based and item-based collaborative filtering.

3.3.2. KNNWithMeans. KNNWithMeans is an extension of the k-Nearest Neighbors (KNN) algorithm, incorporating mean-centered ratings in its prediction process. This algorithm is particularly suited for collaborative filtering tasks in recommendation systems [16].

The key components of KNNWithMeans include:

• Number of Neighbors (k): A predefined number of nearest neighbors to be considered for predictions, similar to the basic KNN algorithm.

• Distance Metric: A measure to quantify the similarity between instances, such as cosine similarity or Pearson correlation coefficient.

• Mean Centering: Unlike KNNBasic, KNNWithMeans adjusts the ratings by subtracting the mean rating of the corresponding user (or item) from each rating. This mean centering helps in reducing the bias due to different user rating behaviors and brings the ratings to a comparable scale.

• Prediction Rule: The prediction is computed by taking a weighted sum of the mean-centered ratings of the k nearest neighbors and adding back the mean rating of the target user (or item).

• Optional Weighting Scheme: Similar to KNNBasic, neighbors may be weighted based on their similarity to the query point.

KNNWithMeans offers an advantage over KNNBasic by considering the underlying rating patterns of users or items, thus providing more personalized recommendations. By centering the ratings around the mean, it mitigates the effects of different rating scales among users, leading to more accurate and robust predictions.

3.3.3. KNNBaseline. KNNBaseline is a specialized form of the k-Nearest Neighbors (KNN) algorithm, designed to incorporate baseline estimates in the prediction process. This algorithm is particularly applicable in collaborative filtering contexts, such as recommendation systems [17].

The key components of KNNBaseline include:

• Number of Neighbors (k): A predefined number of nearest neighbors to be considered for predictions, consistent with traditional KNN approaches.

• Distance Metric: A similarity measure, often Pearson correlation coefficient or cosine similarity, adjusted by baseline estimates, to quantify the similarity between instances.

• Baseline Estimates: Unlike KNNBasic or KNNWithMeans, KNNBaseline considers both user and item biases in its predictions. The baseline estimate for a given rating is calculated as the overall mean rating plus the user bias and the item bias. These biases represent the tendencies of individual users and items to rate higher or lower than the average.

• Prediction Rule: The prediction is computed by taking a weighted sum of the baseline-adjusted ratings of the k nearest neighbors.

• Optional Weighting Scheme: Neighbors may be weighted based on their similarity to the query point, with more similar instances having a greater influence on the prediction.

KNNBaseline offers a more nuanced approach compared to other KNN variants by considering the systematic tendencies of users and items in the rating process. By incorporating these baseline estimates, it provides a more accurate representation of underlying rating patterns, leading to more precise and personalized recommendations.

3.3.4. KNNWithZScore. KNNWithZScore is an adaptation of the k-Nearest Neighbors (KNN) algorithm, incorporating Z-score normalization in the prediction process [18]. This algorithm is particularly relevant in collaborative filtering scenarios, such as recommendation systems.

The key components of KNNWithZScore include:

• Number of Neighbors (k): A predefined number of nearest neighbors to be considered for predictions, in line with traditional KNN methodologies.

• Distance Metric: A measure to quantify the similarity between instances, such as cosine similarity or Pearson correlation coefficient.

• Z-Score Normalization: Unlike other KNN variants, KNNWithZScore standardizes the ratings by transforming them into Z-scores. This is achieved by subtracting the mean rating of the corresponding user (or item) from each rating and dividing by the standard deviation. This transformation brings the ratings to a comparable scale and reduces the bias due to different user rating behaviors.

• Prediction Rule: The prediction is computed by taking a weighted sum of the Z-score normalized ratings of the k nearest neighbors and converting back to the original rating scale by multiplying by the standard deviation and adding the mean rating of the target user (or item).

• Optional Weighting Scheme: Neighbors may be weighted based on their similarity to the query point, as in other KNN variants.

KNNWithZScore offers a more sophisticated approach by considering not only the mean but also the variability in user or item ratings. By standardizing the ratings using Z-scores, it accounts for different rating scales and variances among users, leading to more robust and personalized recommendations.

3.3.5. SVD. Singular Value Decomposition (SVD) is a technique used in recommendation systems to break down a user-item rating matrix into three separate parts. These parts represent underlying patterns in how users rate items[19].

In the context of recommendation systems, SVD serves several purposes:

• Discovering Hidden Relationships: It identifies underlying connections between users and items, helping to understand why certain items are rated similarly.

• Predicting Missing Information: SVD can predict how a user might rate an item they haven't seen before, allowing for personalized recommendations.

• Reducing Complexity: By focusing on the most significant patterns, SVD reduces the amount of data needed to make accurate recommendations, making the process more efficient.

SVD is a powerful tool in collaborative filtering, providing a mathematical way to offer precise and personalized recommendations. Its application is widespread in modern recommendation systems.

3.3.6. Hybrid User-Movie KNN. The KNN algorithm plays a pivotal role in the recommendation system described herein. Initially, the algorithm is employed to identify a cohort of users that exhibit the closest resemblance to the current user, based on a predefined set of criteria. Specifically, the algorithm searches for the 10 users whose preferences or behaviors are most akin to those of the current user, as determined by a suitable distance metric.

Upon identifying these similar users, the system then examines the movies that have been viewed by this cohort but remain unseen by the current user. These films are subsequently designated as candidate movies, forming a preliminary pool for potential recommendation. This selection process ensures that the recommendations are both relevant to the current user's preferences and novel in terms of their viewing history.

Following the identification of candidate movies, the KNN algorithm is once again invoked, this time to process the movie data. The algorithm analyzes the attributes and features of these candidate movies, comparing them to the specific movie input by the user. Through this comparative analysis, the algorithm selects the 10 movies that are closest in similarity to the user's input movie.

The final selection of these 10 movies is predicated on a comprehensive analysis that considers both user similarity and movie attributes. By leveraging the KNN algorithm in this dual capacity, the system is able to provide recommendations that are highly tailored to the individual user's tastes and viewing habits. The integration of user-based and item-based collaborative filtering in this manner underscores the robustness and sophistication of the recommendation process, promising a more personalized and engaging user experience.

3.4. Performance metrics

3.4.1. Cross-validation. Cross-validation is a prevalent method in machine learning for model construction and parameter verification. It involves the division of the dataset into k equal parts, allowing for repeated use of the data through various training and test set combinations.

Cross-validation ensures that all data is involved in training and prediction, reducing the risk of overfitting. However, it may entail a bias-variance tradeoff; choosing the number of partitions (k) requires balancing these aspects. In this study, k was set to 5, optimizing the balance between potential bias and variance.

3.4.2. MSE. The mean square error (MSE) is a standard measure for evaluating a model's performance. It calculates the square of the distance between the predicted value and the actual value (i.e., the error), reflecting the closeness of the predicted value to the true value. Mathematically, the MSE can be expressed as:

\( MSE=\frac{1}{N}\sum _{t=1}^{N}{(observe{d_{t}}-prⅇdictⅇ{d_{t}})^{2}} \)

where observed(t) represents the actual output value (observed value) of data t, and predicted predicted(t) is the corresponding predicted value. A smaller MSE indicates better accuracy, allowing the prediction model to describe the experimental data more precisely.

3.4.3. RMSE. The root-mean-square error (RMSE), also referred to as the standard error, is obtained by taking the square root of the mean square error (MSE). The motivation for employing RMSE is analogous to that of standard deviation; it serves to ensure that the error metric is expressed in the same dimension as the data. Since the MSE is in squared units, taking the square root rectifies this disparity, making the error metric more interpretable. The mathematical expression for the RMSE is:

\( RMSE=\frac{1}{N}\sum _{t=1}^{N}{(observⅇ{d_{t}}-prⅇdictⅇ{d_{t}})^{2}} \)

Here, the RMSE provides a measure of the model's prediction error in the same units as the observed values, offering a more direct reflection of the dispersion degree.

4. Experimental Result

The performance of various recommendation algorithms was evaluated using both the Root Mean Square Error (RMSE) and the Mean Absolute Error (MAE). These metrics provide insight into the accuracy and robustness of the different models. The table below summarizes the results:

Table 1. Formatting sections, subsections and subsubsections.

As shown in table 1, the comparative evaluation of several recommendation algorithms, categorized under " Hybrid User-Movie KNN " methods, is delineated through the application of two widely accepted error metrics: Root Mean Square Error (RMSE) and Mean Absolute Error (MAE). The algorithms under examination include KNNBaseline, which integrates baseline estimates and recorded an RMSE of 0.8793 and an MAE of 0.6769; KNNWithMeans, which adjusts for mean ratings and achieved an RMSE of 0.8789 and an MAE of 0.6760; KNNBasic, representing the foundational KNN approach with an RMSE of 0.8802 and an MAE of 0.6766; KNNWithZScore, employing Z-score normalization and registering an RMSE of 0.8795 and an MAE of 0.6764; and Singular Value Decomposition (SVD), a matrix factorization method, yielding an RMSE of 0.8790 and an MAE of 0.6761.

The results provide a nuanced perspective on the relative efficacy of these algorithms. While the differences in performance are marginal, they offer valuable insights for practitioners seeking to tailor recommendation systems to specific contexts or objectives. The choice between RMSE and MAE as evaluation metrics may further reflect the particular emphasis on either the magnitude of errors or their absolute values. This comparative analysis contributes to the broader understanding of recommendation algorithms, facilitating informed decision-making in their application and optimization.

5. Discussion

The comparative analysis of recommendation algorithms, including KNNBaseline, KNNWithMeans, KNNBasic, KNNWithZScore, and Singular Value Decomposition (SVD), reveals subtle yet insightful differences in their performance. Measured through Root Mean Square Error (RMSE) and Mean Absolute Error (MAE), the results reflect the nuanced characteristics of each algorithm.

KNNBaseline's integration of baseline estimates, KNNWithMeans' adjustment for mean ratings, KNNBasic's foundational approach, KNNWithZScore's employment of Z-score normalization, and SVD's matrix factorization method each contribute to the specific performance metrics observed. While the differences in RMSE and MAE across these algorithms are marginal, they may have significant implications in specific applications or contexts.

The choice of evaluation metrics also warrants consideration. RMSE emphasizes the magnitude of errors, penalizing larger deviations more heavily, while MAE focuses on the absolute values of errors, treating all deviations equally. The selection between these metrics may align with particular objectives or constraints within a recommendation system.

6. Conclusion

This study offers a comprehensive examination of various recommendation algorithms, shedding light on their relative strengths and weaknesses. By employing RMSE and MAE as evaluation criteria, the analysis provides a multifaceted perspective on the effectiveness of each algorithm.

The findings underscore the importance of understanding the underlying characteristics and assumptions of different recommendation algorithms. While no single algorithm markedly outperformed the others, the subtle variations in performance may guide practitioners in tailoring algorithms to specific needs and contexts.

The comparative analysis contributes valuable insights to the field of recommendation systems, enhancing the understanding of algorithmic behavior and facilitating more informed and nuanced decision-making. Future research may explore additional algorithms, diverse datasets, or alternative evaluation metrics to further enrich the landscape of recommendation system research and practice.