1. Introduction

Since particle swarm algorithms have been proposed, improvements for various aspects of them such as control of convergence rate, balance between local and global search have emerged, e.g. Garg [1] proposed GA-PSO for constrained optimization problems where the PSO algorithm module operates towards improving the vectors while the GA module is used for modifying the decision vectors using the genetic operators to take advantage of their common strengths for solving the nonlinear design optimization problems. In addition, Zhan et al. [2] proposed a parameter adaptive control strategy for PSO, which utilizes Sigmoid mapping so the weights can be constantly changed with continuous iteration and state evolution, and different strategies are adopted at different stages of the algorithm operation. In this paper, on the basis of the previous research results, the hybrid particle swarm algorithm is added with an adaptive module to realize that it can stably maintain the convergence speed in the case of short iteration number setting, so as to get the better solution faster, and it is applied to the TSP problem to test its performance. At present, the convergence speed of various swarm intelligence algorithms is relatively satisfactory after continuous improvement, and how to integrate their advantages to make them work well in a wide range of application scenarios is a more important issue in the future.

2. Related work

2.1. Introduction to PSO algorithm

Particle Swarm Optimization (PSO for short) is a computational method in computational science that optimizes a problem by continuously iterating over the candidate solutions given a measure of merit. The algorithm optimizes the problem by setting a group of candidate solutions (particles) and moving these particles in the search space according to a simple mathematical formula that updates the positions and velocities of all particles. The motion of each particle is influenced by its local optimal position, but it is also guided to the global optimal position in the search space, and this global optimal position is also updated with better positions found by other particles [3],with the following basic formula:

\( V_{id}^{t+1}=ωV_{id}^{t}+{c_{1}}{r_{1}}×(P_{id}^{t}-X_{id}^{t})+{c_{2}}{r_{2}}×(G_{d}^{t}-X_{id}^{t}) \) (1)

\( X_{id}^{t+1}=X_{id}^{t}+V_{id}^{t+1} \) (2)

which,

\( V_{id}^{t} \) denotes the velocity of the i-th particle in the t-th iteration in the d-th dimension;

\( ω \) is the inertia weight;

\( P_{id}^{t} \) is the individual extreme value of the i-th particle in the d- th dimension;

\( G_{d}^{t} \) is the global extreme value;

\( {c_{1}} \) and \( {c_{2}} \) are the positive constants that regulate the relative importance of the individual extreme value and the global extreme value;

\( {r_{1}} \) and \( {r_{2}} \) are the random numbers generated randomly on the interval [0,1].

The velocity formula can be divided into three parts. The first part indicates the degree of influence of the current velocity and direction on the next moment. The second part indicates the influence of the optimal position in the particle history information on the next moment at the current moment. And the third part indicates the influence of the optimal position in the particle history information on the next moment for all particles up to the current moment. Obviously, the basic idea of the PSO algorithm is to use the information of individuals and populations to continuously learn and adjust, while parameters such as \( ω \) , \( {c_{1}} \) , \( {c_{2}} \) , \( {r_{1}} \) , \( {r_{2}} \) , are reflected as the algorithm has flexibility.

In practical use, the particle swarm optimization algorithm has the advantages of faster search and simple parameter setting, but it also has the shortcomings of weak global search ability and the fact that the diversity of the population will be reduced at the later stage of the algorithm. In response to its shortcomings, many improvements have been proposed by previous authors, and one of the ideas is to combine it with genetic algorithms, where the introduction of genetic operators can enhance the information exchange between particles and increase the diverse characteristics of the population, and then it is no longer limited to the local optimum [4].

2.2. PSO algorithm applied on TSP problems

In solving the TSP problem, given a set of cities and inter-city accesses and their lengths, our objective is to determine the sequence of visits to a city that minimizes its cost. Therefore, when applying the tsp algorithm, the author choose to make each particle represent a feasible solution (i.e., a sequence of visits). For example, in a tsp problem with five cities, a particle xi = (1, 3, 2, 4, 5) means a visit sequence of 1-3-2-5-4-1, and the fitness function is expressed in terms of the total travel length. Instread, the concept of swap sequence is chosen to be introduced in the representation of the genetic operator with particle update. Still taking the above example as an example, let its selected swap sequence swap=(1, 3) at the time of update, that is, the current sequence of cities in the 1st and 3rd visit swap order to get the new xi=(2, 1, 3, 4, 5). For the swap operation, when we compare two particles, the difference in their sequences can be represented by multiple pairs of swap sequences, such as ss = ((1, 2), (3, 5), (7, 9)), and for the swap sequence to perform the swap operation is equivalent to the swap operator to take place. In addition, when reproducing the variation operation of the original paper, it can also be represented by the exchange sequence, i.e., the occurrence of variation in the tsp problem can be represented as a randomly generated exchange of access order in a sequence.

3. Methodology

3.1. The idea of self-adaptive parameters

All parameters of the hybrid particle swarm algorithm in the original paper are given before the algorithm is run and do not change throughout the iterative process [5]. However, considering that particle swarm optimization has different requirements at different stages of the algorithm's operation, the idea of adaptivity is used to reduce the influence of individual optima and global optima in the early stage, so that the algorithm can explore more extensively in the solution space. In the latter stage, the increasing importance of the individual optima and the global optima can also help accelerate the convergence speed.

To achieve this improvement, the initial values for \( {r_{1}} \) and \( {r_{2}} \) are given, and at each algorithm iteration they are recalculated by using the exponential function based on the current number of iterations and the initial values, ensuring they can continuously increase with the iteration.

3.2. The idea of simulated annealing

A round of iterations of simulated annealing can be briefly described as generating a new solution from the current solution space by a generating function, calculating its difference from the objective function corresponding to the current solution, judging whether the new solution is accepted, and replacing the current solution according to the given criteria. In this algorithm, this idea is applied to the exchange operation using the criterion that when the fitness value of new access order obtained by performing the swap operation is inferior to that of the one before swap, the new solution will not be rejected directly, but will be accepted with a certain probability. By introducing the simulated annealing idea, the particles can have a greater probability of jumping out of the local optimal solution and have a stronger global optimization ability.

And about the probability function, the former part is related to the current number of iterations, while the latter part is related to the relative difference between the fitness of the current solution and the new solution, both of which are calculated using an exponential function of the form \( {e^{∧}}(-i∕j) \) .

3.3. Program flow chart

Figure 1 reflects the basic framework of the improved algorithm. The first two steps initialize each parameter, enter the loop from the lowest three steps, continuously iteratively perform mutation and cross-operation, calculate the fitness of the new solution, and judge whether to accept it until the end condition is met.

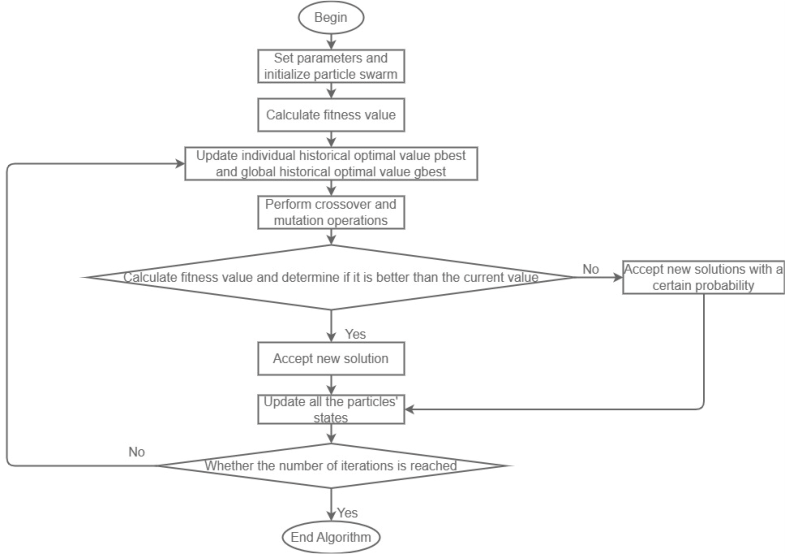
Figure 1. Program Flow Chart

4. Experiments

4.1. Overview of conditions

In the configuration of experimental conditions, the specified parameter cities generated by random seeds is selected in the given range of 100*100 as the conditions for TSP problems to find the shortest path. The algorithm of original paper is used as baseline [4], comparing with our improved algorithm at three iteration counts of 30, 50 and 70.

4.2. Results

4.2.1. 30 iterations result

Improved algorithm generation optimal: 2864.65. Original algorithm generation optimal: 3110.04. The optimal value above shows that improved algorithm performs better when iteration was set 30.

4.2.2. 50 iterations result path map

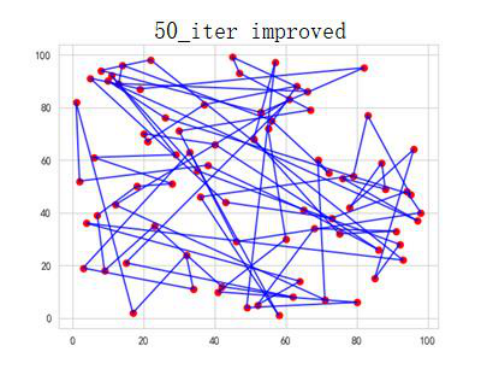
Figure 2. 50 iteration of improved algorithm

Improved algorithm generation optimal: 2712.17

Improved order of access: [71 28 59 29 54 77 70 27 11 15 37 40 36 60 17 72 68 12 4 762 7 52 0 30 14 49 47 10 20 9 26 55 75 19 25 3 16 41 5 61 13 74 38 32 78 79 51 69 1 57 24 64 65 58 50 45 34 67 35 53 8 63 42 21 33 23 31 18 6 39 22 56 73 66 48 44 46 43 62]

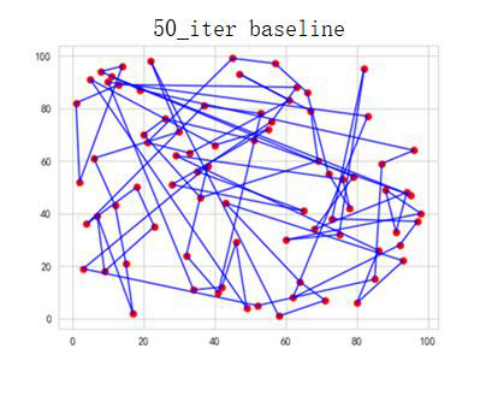
Figure 3. 50 iteration of baseline algorithm

Baseline generation optimal: 2955.52. Baseline order of access: [51 20 75 8 5 15 53 37 11 55 76 32 63 56 7 62 44 46 43 47 26 66 65 73 18 57 35 4 60 68 67 45 64 24 22 49 41 13 19 23 30 40 25 59 36 39 33 71 31 27 74 61 3 79 34 14 21 29 16 52 12 28 50 69 0 42 2 77 17 72 48 54 10 70 58 6 1 389 78].

The comparison between optimal value and the access of order reflects that improved algorithm performs better under the condition of 50 iterations.

4.2.3. 70 iterations result path map

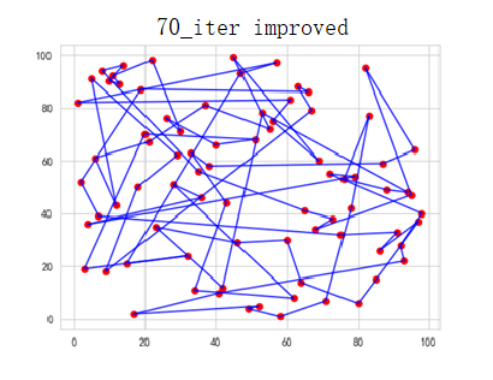
Figure 4. 70 iteration of improved algorithm

Improved algorithm generation optimal: 2158.07. Improved order of access: [71 1 7 26 10 23 58 77 15 37 25 78 74 19 2 76 36 60 20 68 32 39 22 51 0 79 69 70 54 66 64 34 72 65 4 57 45 52 28 50 56 73 30 63 62 46 24 12 67 40 17 44 3 61 42 75 11 21 31 16 49 43 47 59 135 8 9 53 18 6 14 27 48 29 33 55 41 35 38].

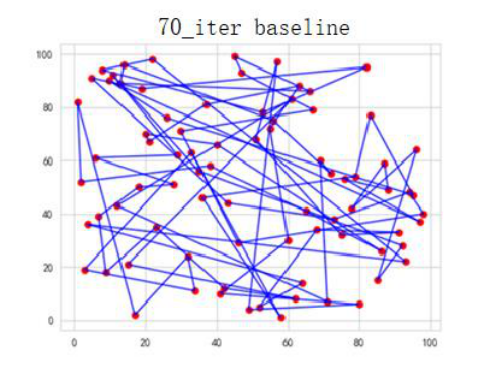
Figure 5. 70 iteration of baseline algorithm

Baseline generation optimal: 2710.74. Baseline order of access: [51 20 75 8 5 15 53 33 11 6 76 7 63 56 32 62 44 46 29 47 26 48 68 73 66 57 35 4 60 36 67 45 64 24 13 78 41 58 19 72 30 40 25 79 65 39 18 31 49 27 74 61 9 59 34 14 21 3 16 52 23 28 50 69 0 42 2 71 17 22 77 54 10 70 12 43 1 55 38 37].

The comparison between optimal value and the access of order reflects that improved algorithm performs better under the condition of 70 iterations.

4.2.4. 70 iteration process diagram

As Figure 6 shows, when iteration value was set 70, the convergence speed of baseline algorithm slows down after 15 iterations, while the improved algorithm keeps the speed relatively stable.

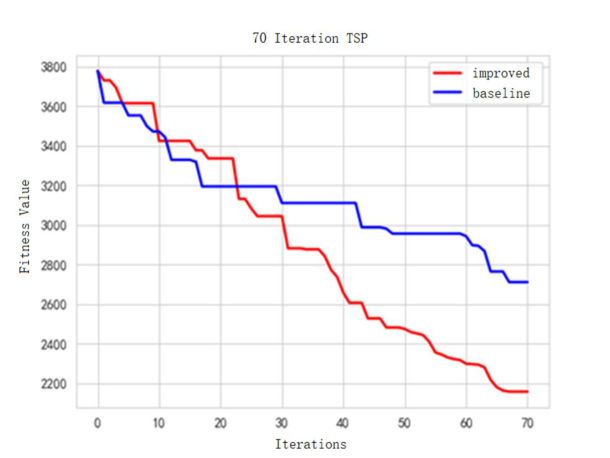
Figure 6. Line chart of 70 iterations’ fitness value

5. Conclusion

The above experimental results and Figure 2-6 show respectively that the improvements we have made can optimize the algorithm to a certain extent at 30, 50, 70 iterations, and it is mainly because the improved algorithm can maintain the convergence speed stable for more iterations. However, the algorithm can still be further improved. The first is judgment about the end of the loop. Currently, only the number of iterations is used, and new judgment conditions related to fitness can be added in the future. And the second is that the performance of the improved algorithm will decrease when the given number of iterations is too large, further research is needed in this aspect.