1. Introduction

In the preparation stage of traditional open surgery, surgeons need to determine the different physiological characteristics (such as abdominal cavity size, abdominal wall thickness, lesion position, etc.) of different patients according to medical images, and make targeted surgical planning [1].The application of robot technology in the field of open surgery can solve some shortcomings of traditional open surgery, such as the physiological jitter of the doctor, the tremor of the window during the operation, etc. Reasonable trajectory planning can significantly improve the accuracy of surgical operation and the success rate of surgery, and can also achieve the purpose of reducing the length of the incision path, reducing postoperative pain and shortening postoperative recovery time [2].In robotic laparotomy, it is necessary to formulate a reasonable trajectory planning scheme. The content of trajectory planning can be summarized as: identification of surgical incision, planning of surgical incision trajectory.

The trajectory planning problem of open surgery is a special and typical multi-joint robot trajectory planning problem[3,4]. In the algorithm of robot trajectory planning, there are many researches on the robot trajectory planning algorithm under the optimal path[5,6]. In recent years, the use of intelligent methods to optimize the trajectory method has become a hot spot. The purpose is to make its accuracy and distance optimal given its path points [7].It has certain guiding significance for the trajectory planning of surgical robot in clinical application [8].Due to the non-linear nature of the surgical incision itself and the high real-time requirements of the robot system, it is very difficult to accurately solve it. Therefore, it is feasible to use genetic algorithm to optimize the problem solution [9].Although the existing robot trajectory planning algorithms are very rich, and there are many excellent planning strategies with high maturity, they are difficult to meet the above various interrelated and influential performance indicators at the same time[10,11]. For example, shortening the movement time of the robot and increasing the speed and acceleration of the robot may cause excessive torque; The motion angle of each axis and the amount of end execution may be large, increasing the operation time and risk. [12].These performance indicators will affect the accuracy and success rate of open surgery[13,14,15].

In this paper, a method based on machine vision and improved genetic algorithm is proposed to solve the trajectory planning of open surgery of surgical robot. The contour curve of human open surgery incision is extracted from the image by feature recognition algorithm, and then the curve is discretized and integrated into the trajectory planning stage. Based on the discretized model, the optimal surgical incision trajectory is identified, and the spline curve is segmented by combining the biological characteristics of the human abdomen and the improved genetic algorithm (GA). Trajectory planning, and optimize the minimum number of segments. Finally, the trajectory planning results are converted to Cartesian space for programming according to the spatial pose relationship, and the optimal surgical tool path is obtained to realize the trajectory planning of surgical robot laparotomy.

At present, there are few examples of applying the improved genetic algorithm to the trajectory planning of surgical robots by modeling the biological characteristics of human abdomen and combining with machine vision. This paper studies the above problems and expounds the methods of the process.

2. Process description

2.1. Surgical robot open surgery

This paper focuses on the trajectory planning of the incision of the skin and subcutaneous tissue by the surgical robot.

2.2. Robot calibration

The mutual translation distance of the robot, the bracket and the camera refers to the basic drawings and placement positions. When placed, the z-axis of each coordinate system is vertical, parallel or collinear. First, the robot is calibrated, as shown in Figure 1. Because the end tool axis is parallel to the z-axis of the sixth axis of the robot, the TCP and the end center point do not change the upper orientation, only move in the position, and the tool coordinate system calibration method adopts the ' three-point method '. Through the calibration of the tool coordinate system, the coordinate position relationship between the robot end and the tool is established. \( {{^u}C_{h}} \) is defined as the coordinate of TCP in the world coordinate system, which is also the origin of the user coordinate system. \( {{^u}T_{e}} \) is the translation matrix between the two. The coordinate relationship established by the calibration of the tool coordinate system is expressed as

\( {{^u}C_{h}}={{^u}T_{e}}\cdot {{^e}C_{h}} \) (1)

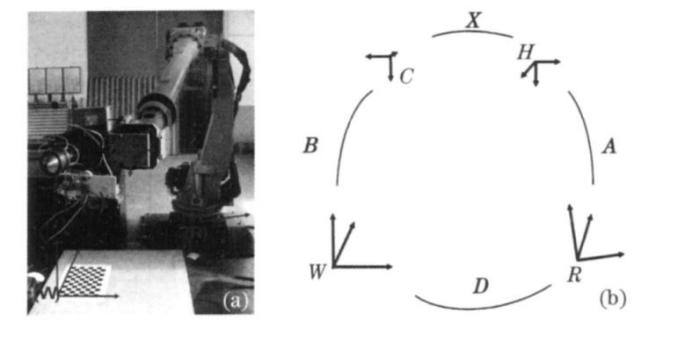
Figure 1. Hand-target-eye calibration coordinates[16]

The calibration of the user coordinate system requires the use of a lattice plate, which is placed on the x-y plane of the user coordinate system. The plane where the lattice plate is placed is also the median sagittal plane of the human abdominal incision. The position of the center point of the lattice plate is defined as the origin of the user coordinate system, and the TCP of the teaching robot points to this point. The transformation relationship between the origin of the user coordinate system and the base coordinate system of the robot is determined by kinematics.Several coordinate points in the horizontal and vertical directions of the lattice plate are taken to determine the x-axis and y-axis directions of the user coordinate system, and then the z-axis direction is determined.

\( {^u}C \) is defined as the coordinate in the user coordinate system. By calibrating the user coordinate system, the relationship between the two can be established:

\( {^u}C={{^u}T_{r}}\cdot {{^u}R_{r}}\cdot {^r}C \) (2)

Place the dot matrix plate at the target position and take a picture. The point spacing of the lattice plate and the focal length \( f \) of the camera are known. The points in the picture are identified by computer to obtain the recognition offset matrix, and several points with large recognition errors in the matrix are removed. Finally, the dot matrix with high recognition accuracy is used as a sample for visual calibration calculation. Based on the theory of camera monocular vision calibration, the monocular vision calibration of the camera can be completed with the input of accurate dot matrix samples and known parameters.

Define \( {^c}C \) is the corresponding coordinate of the camera coordinate system, \( {{^c}H_{v}} \) is the internal parameter matrix between the image coordinate system and the camera coordinate system, and \( {^v}C \) is a pixel point of the image coordinate system. Camera calibration establishes the relationship between the two:

\( {^c}C={{^c}H_{v}}\cdot {^v}C \) (3)

The external parameter equation between the camera coordinate system and the user coordinate system is:

\( {^u}C={{^u}T_{c}}\cdot {^u}R\cdot {^c}C \) (4)

\( {^b}C \) is defined as the coordinate of the base coordinate system. The corresponding posture matrix of robot \( {{^e}H_{b}} \) can be obtained by calling relevant interface function.

\( {^e}C={{^e}H_{b}}\cdot {^b}C \) (5)

According to the inverse kinematics solution, the motion angle of each joint is:

\( θ=[{θ_{1}},{θ_{2}},⋯,{θ_{6}}{]^{T}}={F^{-1}}[{{^b}C^{-1}}\cdot {^e}C] \) (6)

Therefore, with the user coordinate system as the spatial relationship link, the spatial pose transformation relationship of hand-target-eye is established.

2.3. Image recognition and trajectory planning

The camera is used to identify the contour of the open surgical incision of the human body. Keep the position of the camera unchanged. In the images captured by the camera, the lower part of the human abdominal surgery can be artificially selected from the pictures displayed by the instrument. The abdominal curve features in the selected area will be extracted according to the algorithm.

After the contour features of the abdominal curve in the region are identified, the algorithm will give an initial point of TCP close to the curve features according to the geometric features of the curve. According to the expected entry position, the initial point is transferred to the entry point of the tool path, and the spatial coordinates of the point are obtained by Equation (4). The location of the entry point should be adjusted according to the different physiological characteristics of different patients.

After recognizing the contour curve of the human abdomen, the spatial pose of each point on the curve can be calculated by the hand-target-eye spatial kinematics relationship. In theory, the robot can refer to the curve trajectory to complete the cutting task. However, the abdominal curve is a high-order function curve, and there is no suitable decoder for the surgical robot to complete the continuous motion planning of this high-order spline curve. Similar to the problem of complex numerical control curve fitting, we use arc interpolation or linear interpolation to solve it.

Because the contour curves of the lower part of the abdomen of different patients are slightly different, the arc interpolation method is not reliable and is not considered for the time being. The continuous line segment trajectory interpolation method is mainly used to fit the entire contour curve using continuous multi-segment straight lines. The characteristics of the contour curve of the lower part of the abdomen are very obvious in the selected area of the image box. The coordinates of a large number of pixels on the contour curve are extracted by the method of pixel gray step, and the characteristic function is obtained by m-order spline fitting:

\( {F_{v}}(x)=\sum _{t=0}^{m}{a_{t}}{x^{t}} \) (7)

According to Equation (4), in the user coordinate system, the first and last two points \( {P_{0}} \) , \( {P_{n}} \) , \( n+1 \) are the total number of path points, \( n∈N \) . A straight line can be obtained by connecting the first and last two points:

\( {F_{0-n}}(x)={P_{0,y}}+[({P_{n,y}}-{P_{0,y}})/({P_{n,x}}-{P_{0,x}})](x-{P_{0,x}}) \) (8)

As shown in Figure 2, the line segments between the first and last points are divided into n line segments. Do the vertical line of \( {F_{(0-n)}}(x) \) at the adjacent points of all line segments:

\( \begin{cases} \begin{array}{c} {f_{i}}(x)=[({P_{0,x}}-{P_{n,x}})/({P_{n,y}}-{P_{0,y}})](x-{V_{i}})+{U_{i}} \\ {U_{i}}={P_{n,y}}+\frac{i({P_{0,y}}-{P_{n,y}})}{n-1},i=1,⋯,n-1 \\ {V_{i}}={P_{n,x}}+\frac{i({P_{0,x}}-{P_{n,x}})}{n-1},i=1,⋯,n-1 \end{array} \end{cases} \) (9)

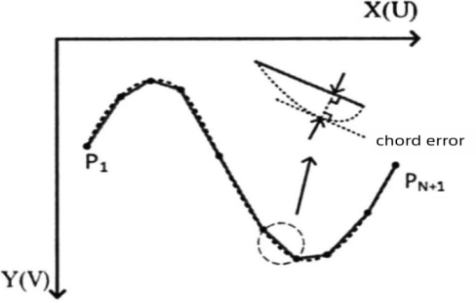
Figure 2. Principles of segmented path planning[17]

The \( n-1 \) intersection points of \( {f_{i}}(x) \) and \( {F_{v}}(x) \) are obtained. The bow height error between the line of two path points and the curve is the chord error. Firstly, the coordinate \( ({x_{i}},{F_{v}}({x_{i}})) \) is calculated to conform to:

\( {{F_{v}}^{ \prime }}({x_{i}})=\frac{{P_{k-1,y}}-{P_{k,y}}}{{P_{k-1,x}}-{P_{k,x}}} \) (10)

Where, \( i=1,⋯,n-1,k=1,⋯,n,{F_{v}}({x_{i}})∈({P_{k-1,y}},{P_{k,y}}) \)

The chord error of the fitting line segment i is as follows:

\( \begin{cases} \begin{array}{c} {ε_{i}}=\frac{|{M_{{x_{i}}}}-{F_{v}}({x_{i}})-M{P_{k-1,x}}+{P_{k-1,y}}|}{\sqrt[]{{M^{2}}+1}} \\ M=\frac{{P_{k,x}}-{P_{k-1,x}}}{{P_{k-1,y}}-{P_{k,y}}},i=1,⋯,n-1,k=1,⋯,n \end{array} \end{cases} \) (11)

The chord error caused by curve segmentation fitting is difficult to avoid. However, the human abdomen has a peritoneal cavity, that is, the parietal peritoneum and the visceral peritoneum continue and migrate with each other, forming a potential gap, as shown in Figure 3. The physiological structure of the peritoneal cavity is exactly an error buffer layer for open surgery. If the chord error is controlled within the range of the buffer layer, the above method is feasible. Moreover, the discretization of the curve can reduce the length of the incision path, thereby reducing the postoperative pain of patients, and then shortening the postoperative recovery time. The thickness δ of the peritoneum is determined, and the thickness δ is used as the thickness of the buffer layer. The minimum number of segments n can be optimized by GA.

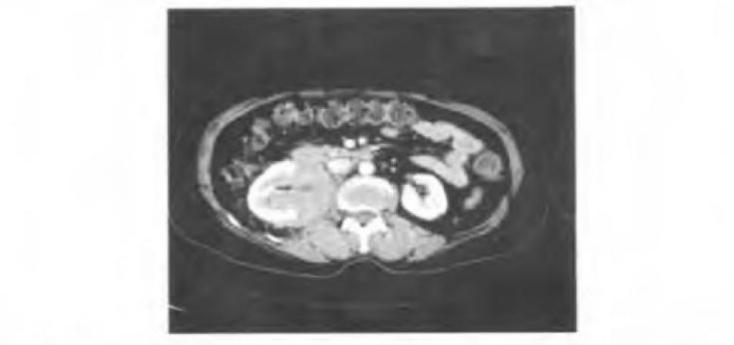
Figure 3. Cavum peritonaei shown by axial unenhanced CT[18]

GA often uses roulette to retain the next generation, which often misses some good genes, so that the population can not develop well, and even 'reverting' phenomenon. If the selection of crossover and mutation rate is not careful, there will be 'premature' phenomenon. After each iteration of the algorithm, the improved GA retains the gene group with the highest fitness and replaces the population with the lower fitness of the next generation, which can solve the phenomenon of 'reversion'. The algorithm flow is shown in Figure 4.

In addition, the improved GA uses an adaptive way to increase the activity of the population. After several generations of iterations, when the algorithm finds signs of 'precocity', it will automatically adjust the probability of recombination, crossover and mutation to prevent the population from falling into a local optimal state. If the 'precocity' phenomenon is avoided, the default probability is restored. Through the above changes, the improved genetic algorithm can converge to the optimal solution stably and quickly, and its gene fitness function is:

\( {f_{k}}=({u_{0}}+{u_{1}}\sum _{i=1}^{n}{ε_{i}})/{u_{2}}{v_{k}} \) (12)

Where \( {f_{k}} \) is the fitness function of the gene, \( {v_{k}} \) is the floating point value of the \( k \) gene (the number of path points), \( {ε_{i}} \) is the chord error of the \( i \) segment, and \( {μ_{0}},{u_{1}},{u_{2}} \) is the weight coefficient. The weight coefficient can balance the influence of various limiting factors on the fitness, and can adjust the weight coefficient according to the importance of each item of the fitness function. The weight coefficient function is:

\( {u_{0}}={k_{0}},{u_{2}}={k_{2}} \) (13)

\( {u_{1}}=\begin{cases} \begin{array}{c} 0,{ε_{1}} \lt δ \\ {k_{1}},{ε_{1}}≥δ \end{array} \end{cases} \) (14)

Through the formula (9), (10) to calculate the unknown n-1 discrete path points and through the formula (6) inverse solution of all n+1 path points of Cartesian space coordinates, finally teach programming.

The method of human open surgery is generally an empirical teaching-reproduction method. In the preparation of surgery, feature recognition is the first step. The parameters in the identification process need to be combined with the physiological characteristics of the patient and the actual experience of the attending doctor. After starting the surgical procedure, the surgical robot will get the curve entry point according to the image, and finally call the teaching program to start the surgical robot for laparotomy.

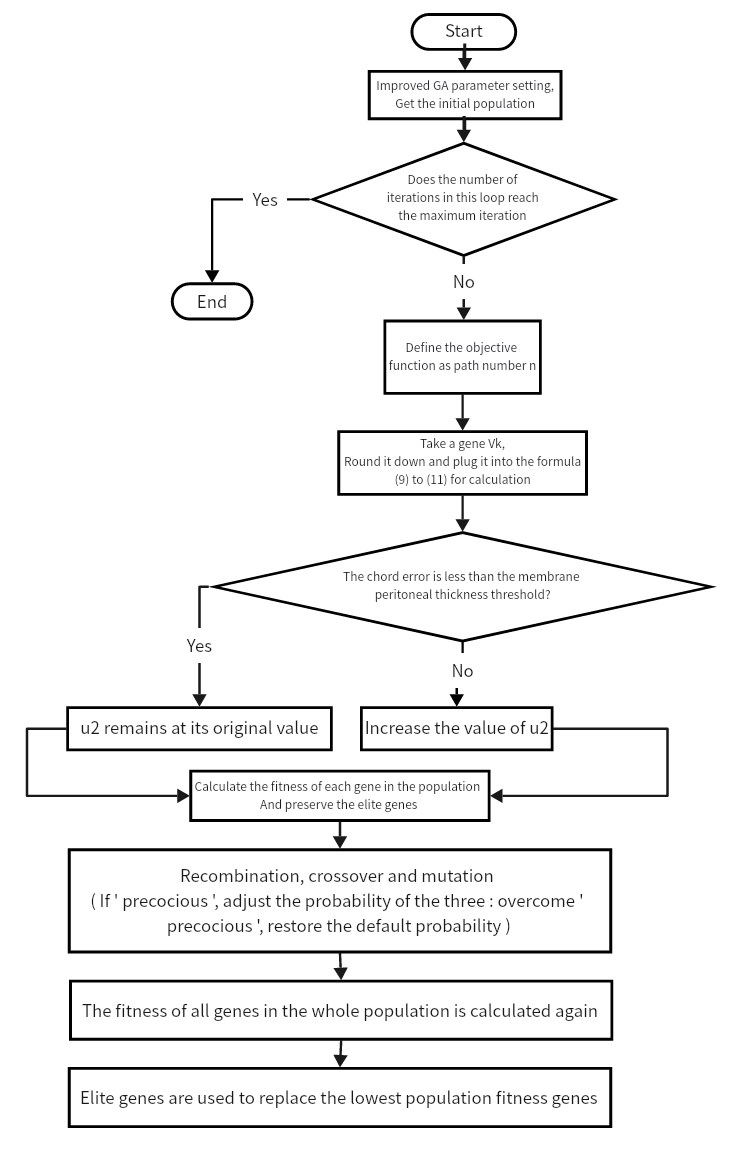
Figure 4. Trajectory planning based on the improved GA[19,20]

3. Experiment results

The probe-probe method was used to measure the "hand-eye-target" calibration error. The coordinates of the probe vertex in the image coordinate system are obtained, and the coordinates of the corresponding world coordinate system are solved to control the TCP to reach the point. Based on the existing errors in coordinate system conversion calculation, spatial position measurement and robot mechanical transmission, and according to the surgeon 's experience and the physiological characteristics of patients with CT plain scan at the operation site, the empirical value of peritoneal thickness of adult human body is 1.5mm ± 0.5mm.In the algorithm, the minimum value of 1mm is taken as the chord error threshold, and the chord error \( ε \) should be included in the buffer layer of the biological model to ensure that the visceral peritoneum is not damaged after cutting.

The main parameters of the genetic algorithm and the improved genetic algorithm are the same. The difference is that the improved genetic algorithm adds the elite population and the adaptive mutation probability in the operation process. The GA operation is prone to the phenomenon of ' reversion ', and the improved GA does not have this phenomenon. According to the contour curve of feature extraction, the multi-line segment optimization is carried out, and the integer 10 is obtained by the convergence of the least path points.

In the experiment preparation phase, the relative positions of the components were arranged and the robot was calibrated. First start the whole control program. Then, the images were collected by CT plain scan, and the coordinates of several waypoints were obtained by image recognition and converted into the robot base coordinate system. The contour photos of the human lower abdomen are transmitted to the computer to extract the contour curve. The points at different positions are extracted on the curve and the curve is fitted with a function. The chord error, cumulative calibration error and contour curve fitting error between the fitting path and the actual path are all within the allowable range of peritoneal thickness. Finally, the robot completes the laparotomy operation according to the motion command and returns to the initial position. The robot performs surgery according to the optimization results. In theory, it can cut the abdominal skin of the human body without damaging the dirty peritoneum and the intestine, which meets the experimental requirements.

4. Conclusion

With the rapid development of robotics and medical technology, open surgery robots have been more and more deeply studied and widely used. Accurate and stable trajectory planning is the key to open surgery robots. Aiming at this problem, this paper proposes a trajectory planning technology for open surgery of surgical robot based on machine vision and improved genetic algorithm. The combination of surgical robot and machine vision is applied to human abdominal surgery to improve the accuracy and success rate of laparotomy, so as to reduce the length of incision, reduce postoperative pain and shorten postoperative recovery time. For the surgical process, the identification and path planning of the abdominal curve is the key to affect the experimental results. Through this experiment, the feasibility and practicability of the whole method are verified. The next step will be to combine the theory with the clinical laparotomy.