1. Introduction

Nowadays, video games are increasingly dominant in the market and the corresponding technologies are constantly improving. With the aim of researching effective algorithms for game map generation, our team focused on procedural content generation, and seek out several algorithms that are of utility. Our study is conducted in Perlin noise, a procedural generation algorithm. To track the development and improvements of Perlin noise, our team select several algorithms that derive from Perlin noise, explaining the process of overcoming its drawbacks, and introducing the improvements which solve its lacks.

2. Background

The procedural generation of maps in games greatly increases the playtime and enjoyment of players. According to Nicolas A. Barriga[1], Procedural Content Generation is the automation of media production, and it has the potential to reduce development cost and developer time, which can be used to add/improve features in the product. Also, through procedural content generation, parts of the game can be randomly generated each game, and the replayability can be enhanced significantly. After analysing of chosen procedural content generation algorithms, our team select Perlin noise as our object of study and the reason for it is as followed:

1. Popularity: Perlin noise is prevalent in games, especially in the aspects of visual elements generation.
2. Wide Application: Perlin noise enables game developers to handle various content generation, including 2D and 3D game texture.
3. Speed and Simplicity: Perlin noise can generate complex patterns with high efficiency, and the execution time is relatively small compared with other procedural content generation algorithms.

2.1. Terminology

1. Noise: Perlin defined a noise function Noise()[2], which is a good texture modeling primitive since we may use it in a straightforward manner to create surfaces with desired stochastic characteristics at different visual scales, without losing control over the effects of rotation, scaling, and translation.
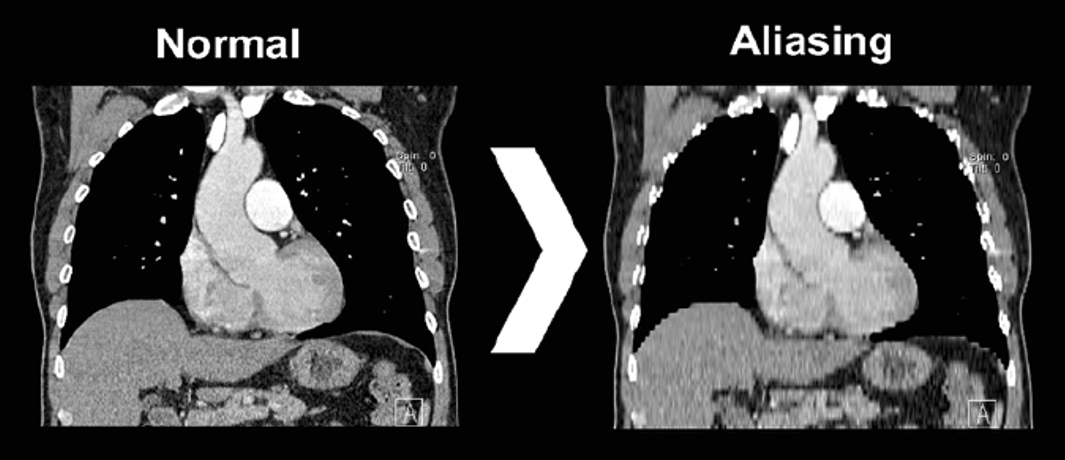
2. Aliasing artifact: Aliasing artifact appears only in the phase encoding axis of current MR imaging systems and can be directly influenced by the radiologist/technologist's choice of image parameters. [3] Aliasing artifact can reduce graphics quality of game surface dramatically by making textures and terrain look unnatural. Figure 1 shows how it affect graphics quality.

3. Perlin Noise

Perlin Noise was first proposed by Ken Perlin in 1985 and then improved in 2002. It is a high performance noise algorithm which can be used in any dimension and usually have a good quality. Although there are some better noise algorithm, it is still popular used in game development, since it is easy to understand and implement.

3.1. Generation Principle

In Perlin Noise, it will divide a coordinate system into pieces of lattice with uniform size, which is normally 1. Then, each peak will get a vector of length 1. In this way, each time, when using Perlin Noise to get the noise value of a point, the algorithm will find out distance vector between peaks around it and itself, and dot product this distance vector with the gradient vector of that peak. All those vectors will be used to do a interpolation to get the weight of each vector and the final noise value. Doing a interpolation can make the noise look smoother and here is the ease curve for interpolation used in 1985: [2] \[ s(t) = 3t^2 - 2t^3 \]

\begin{tikzpicture} \begin{axis}[title=Comparison of Two Ease Curve,grid=both,minor tick num=1] \addplot[color=black,domain=-0.25:0,forget plot]{0}; \addplot[color=black,domain=1:1.25,forget plot]{1}; \addplot[color=gray,domain=0:1]{x}; \addplot[color=green,domain=0:1]{-2*pow(x, 3)+3*pow(x, 2)}; \addplot[color=red,domain=0:1]{6*pow(x, 5)-15*pow(x, 4)+10*pow(x, 3)}; \legend{Linear,Cubic (1985),Quintic (2002)} \end{axis} \end{tikzpicture}

3.2. 2002 Improvement

In 2002, Perlin improved his algorithm to make it more efficient and have a higher quality. [4] In this version, the algorithm will not use a random vector for each peak. All vectors for peaks are chosen from a fixed array. This new algorithm also have a better ease curve for interpolation. \[ s(t) = 6t^5 - 15t^4 + 10t^3 \] Using a value between 0 and 1, the first and second derivatives of this new curve is 0, which means that the noise generated could be smoother at junctions of lattices. [4] Actually, the new algorithm could be faster because it does not need to do expensive floating point multiplication caused by random vectors. However, a more complex interpolation will slow its speed. Thus, this algorithm is only about 10% faster than the original one. However, for high-dimensional noise generation, Perlin Noise's generation speed is still slow because of the exponential time needed to generate and interpolate between  \(2^n\)  vectors at every point, on top of the exponential number of points. Therefore more complex but faster algorithms have been developed, such as simplex noise.

3.3. Issues

Although Perlin Noise can satisfy many situations, it still has some problems. For example, its performance is not good when generating high dimensional noise because of a time complexity of  \(O(2^n)\) . Besides, the noise generated by Perlin Noise also have some manual and directional marks. In order to solve those problems, there are many other algorithms, like Simplex Noise and Wavelet Noise, which have different applications.

3.4. Layered Perlin Noise

By generating multiple Perlin Noise samples at increasing frequency but decreasing magnitude, then overlaying them together, fractal noise can be generated. Each layer is called an octave. For a map generation example, each noise layer represents smaller but more number objects, like mountains to hills to rocks. The frequency increases (number) but the amplitude (size) decreases. Although layering octaves increases generation time, it is worth the cost. Many games use layered Perlin Noise with erosion algorithms to generate natural terrain.

4. Simplex Noise

From previous sections, we have established that the time complexity for Perlin Noise is  \(O(2^n)\) , which means that as the dimension of noise becomes higher, the algorithm's execution time increases exponentially. At the same time, there will be more permutation and interpolation operation and it will also be more difficult to code and maintain. In this way, at 2001, Ken Perlin optimised Perlin Noise and overcame many of its drawbacks, and this algorithm is named Simplex Noise. A more detailed information about why Simplex Noise is better will be described later. [5]

4.1. Main Difference Compared with Perlin Noise

The main difference between Perlin Noise and Simplex Noise is that Simplex Noise uses simplices instead of simple lattice. For example, when generating two dimensional noise, the unit shape for Simplex Noise is an equilateral triangle while Perlin Noise's is a square.

4.2. Generation Algorithm

Thus using Simplex Noise to find the value of a point  \(P\)  would be like this:

1. Find out which simplex  \(P\)  is in.
2. Calculate the vector from each lattice point to  \(P\) .
3. Get the gradient value for each vertex.
4. Weighting each gradient vector and get the final noise value or gradient.

In this procedure, step [???] and [???] are very similar to Perlin Noise and the difficult part would be step [???] and [???] which are how to find out which simplex the point  \(P\)  is in and how to calculate the vector between each lattice point and  \(P\) . The solution is to skew the simplex lattice into a square grid, which is much easier to calculate. [6]

In order to achieve such transformation, some formulas can be used to calculate the coordinates of a point and here is a two dimensional version: ( \(x\)  and  \(y\)  is the coordinate in simplex lattice;  \(x'\)  and  \(y'\)  is the coordinate in a square grid) \[x' = x + (x + y) * F\] \[y' = y + (x + y) * F\] \[F = \frac{\sqrt{n+1}-1}{n}\] And the reversed formulas would be like this: \[x = x' - (x' + y') * G\] \[y = y' - (x' + y') * G\] \[G = \frac{1-\frac{1}{\sqrt{n+1}}}{n}\]

4.3. Advantages

When generating a three dimensional noise using Perlin Noise, it needs to do a total of 24 multiplies, because there will be three multiplications on each eight vertexes of a regular cube. However, multiplication is very expensive on hardware. Therefore, people need a new algorithm which can generate noise using fewer multiplies and having a even better result. Using such a "screw" design, the times of multiplication decreases substantially and it will be more difficult for people to find out the screw. This is also the reason why Simplex Noise would be less directional. [5] Simplex Noise have many advantages compared with Perlin Noise. For instance, Simplex Noise works better at higher dimensions, since the time complexity of a classical noise algorithm and Perlin Noise is  \(O(n^n)\)  and  \(O(2^n)\)  respectively while Simplex Noise only has a time complexity of  \(O(n^2)\)  in a  \(n\)  dimensional noise. [7] It usually has no noticeable directional artefacts and a more continuous gradient, which means that the image generated by Simplex Noise will be more natural and people will find fewer manual marks on it. It can also be implemented in hardware much easier than Perlin Noise because of its fewer multiplications and less dependence on the presence of tables. Perlin even mentioned some ways to optimise this algorithm for hardware. For example, the whole process would be fairly inexpensive if it is worked in a limited bit depth. [5] Using Simplex Noise, it is much easier to get a more complex and clear image or terrain in maps. Besides, it will usually spend less time for Simplex Noise to calculate and render. Here is a demo (depends on noisejs):

5. Wavelet Noise

Despite the noise functions introduced by Perlin becoming increasingly popular for their simplicity and speed, several problems still exist. Before constructing noise patterns, the band of noise that limited to a range of frequencies are collected. The different bands are able to construct complex noise patterns. However, part of Perlin bands contain both needed low frequencies and excessively high frequencies. In this situation, if the band is excluded, the generated game map would lose part of details, otherwise aliasing artifacts would be caused. Another severe problem is that the 2D surfaces sampled by 3D noise will not be band-limited so that the former problem cannot be solved simply by employ a band-limited 3D function.[8] The same problems would happened if simplex noise is used because of the similarity in band. The wavelet noise, a derivative product of Perlin noise, is constructed to overcome these drawbacks.

5.1. Generation Algorithm

In paper Wavelet Noise, Robert L. Cook and Tony DeRose address the problems for special scenarios that the loss of detail is unacceptable by adopting wavelet noise. To construct and analyse wavelet noise, the wavelet analysis [9,10], also known as multiresolution analysis is used by them. Their algorithm in two-dimensional cases consists of multiple steps:

1. Create an image R filled with random noise
2. Downsample R to create half-size image R \(^{\uparrow}\) 
3. Upsample R \(^{\uparrow}\)  to a full size image R \(^{\uparrow\downarrow}\) 
4. Subtract R \(^{\uparrow,\downarrow}\)  from the original R to create noise band N
5. Construct multi-resolution noise  \(M(x)\)  by using noise band  \(N\) 
6. Model the way of noise that used in rendering process
7. Render the game content

In step [???], the pixels typically are constructed by filter kernel and scene function. In this paper, Robert and Tony utilized the orthogonality between the fine scale versions of noise band  \(N(x)\)  and renderer's filter kernel  \(K(x)\)  in specific conditions. \[\int N(2^jx-l)K(x-i) dx=0\] Under this circumstance, they choose an uniform quadratic B-spline basis function  \(B(x)\)  as filter kernel, and the reason for it is as followed:

1. The  \(B(x)\)  can be applied by most renderers for its good approximation;
2. It promises the computationally efficient because since it has small support and low degree;
3. It generates differentiable noise that is useful in procedual content generation.

The wavelet noise bands constructed in this step will lie in the wavelet space and the problem that the constructed noise band with excessively wide range of frequencies will be overcome. For the second issue that the 2D noise sampled by 3D noise will not be band-limited, Robert and Tony bring to the method of wavelet orthogonality machinery. Instead of simply point sampling, they perform a special line orthogonal to 2D surface, assuring the orthogonality condition. The wavelet noise, overcoming these significant issues, has great potency to improve the game content quality.

5.2. Advantages

Wavelet noise has better performance in procedural content generation when comparing with Perlin noise or Simplex noise. Figures 7 and 8 demonstrate wavelet noise has higher performance, surpassing the image created by Perlin noise and achieving the optimal tradeoff between detail and aliasing.

6. Conclusion

In conclusion, our study documents and explains the development of noise generation algorithms. Through an analysis of multiple research papers, we have introduced the principle of Perlin noise and improvements upon it. Through the efforts of scholars, the Perlin noise and its derivatives have overcome numerous issues, including the problems of complexity, loss of details as well as aliasing artifact. The improvement process for Perlin Noise is shown in figure 9.

As we confront the game map generation, the implications of our research are far-reaching. Our literature review can be regard as a reference for algorithm researchers to develop game algorithms and enable them to avoid unnecessary effort. Also, the game developers will benefit from this article as it provides useful details and evaluation to choose between noise generation algorithms.

Acknowledgment

We would like to express our deepest gratitude to Dr. William Nace for his guidance and insights throughout the course of this research project. His expertise and encouragement have been invaluable.