1. Introduction

Group decision making (GDM) is the process by which multiple individuals come together to participate, negotiate, discuss, and select the best solution from a set of possible options. The problem of group decision-making is ubiquitous in daily life and is closely related to people. For example, the management of the company formulates the company's development strategy, the team members negotiate teamwork projects, and various government departments, experts, scholars and social representatives jointly decide on public policies. With the development of information technology and data science, the amount of information has increased dramatically, and the problems to be solved have become increasingly complex [1]. Individual decision-makers are relatively lacking in knowledge and experience, and the information they have is not comprehensive enough, so it is difficult to fully consider all aspects of the problem, and there is inevitably subjectivity and arbitrariness in the decision-making process. In contrast, the study of group decision-making can make full use of the experience and wisdom of multiple decision-makers, give full play to the advantages of different knowledge structures, overcome the shortcomings of a single decision-maker, and improve the objectivity and accuracy of decision-making. With the development of society, more and more people participate in decision-making activities, and the complexity of decision-making also increases, which makes group decision-making more important.

Most of the traditional group decision-making problems assume that decision-makers are independent of each other and ignore the connections between them [2]. However, in actual group decision-making, there may be specific relationships between decision-makers, such as friends, superiors and subordinates, relatives, etc., which may affect the decision-making results. Communication and interaction between decision-makers may lead them to consider the opinions of others, and experienced decision-makers may influence other decision-makers. Therefore, social relations are an important feature of decision-makers, and they are also an urgent factor to be considered in the process of group decision-making [3]. In practice, group decision-making will be more conducive to making accurate and feasible decisions if it can take into account the connections and interactions between decision-makers.

At the same time, the development of social networks and online communities has accelerated the interaction and information transmission between decision-makers, facilitated group decision-making, and attracted much attention to social network group decision-making (SNGDM). On the one hand, social networks are used as a platform for information exchange and communication, and the social relationship between users has increasingly become the main factor influencing decision-making behavior [4]. Social networks can be used to study the relationships between users. Some studies have shown that social networks play an important role in decision-making, such as providing information and knowledge, sharing advice based on trust, and influencing interactions [5]. Therefore, the problem of group decision-making in social networks is a topic worthy of in-depth study.

Different from the traditional group decision-making problem, which is guided by the consensus of decision-makers, the social network group decision-making problem considers the impact of network expansion on the decision-making results, and incorporates the relationship between decision-makers into the decision-making process [6]. For example, in social networks, people express their views and opinions through social media platforms or other channels, providing a new source of information for decision-makers. In addition, in some practical problems, the relationship between group decision-makers will also have an important impact on the decision-making results, for example, in the decision-making within the company or the government, the cooperation and competition between decision-makers will directly affect the decision-making results [7]. Therefore, the study of group decision-making in social networks has a wide range of application scenarios and important research significance.

The traditional approach to group decision-making considers that the members involved in decision-making are independent of each other and have no other connection between members. However, with the rapid development of network technology and the widespread utilization of social media and applications, decision-makers can communicate and exchange freely in the process of group decision-making, and this interaction promotes the evolution of decision-makers' views and accelerates the transmission of information [8]. A social network is a topological structure in which each node represents a member, including individuals, teams, and communities, and the lines between nodes represent interdependencies.

The group decision-making method based on social network analysis (SNA) models the relationship between decision-makers, so as to better understand the connection and interaction behavior between decision-makers. The three main elements of social network analysis are the decision-maker set, the relationship itself, and the decision-maker attributes [9]. It studies the relationships between social network entities, such as members of an organization, company, or country, and analyzes the structure and location attributes of nodes, such as centrality, prestige, and structural balance, among others. Based on social network analysis, it focuses on the social relationship between nodes and edges, and can accurately and clearly describe and characterize the mutual relationship between decision-makers, including the relationship of interest and trust.

2. Related Work

Trust is an essential component in group decision-making (GDM), impacting various models like trust propagation, trust-based consistency, and conflict resolution through trust networks. Trust in GDM can arise from past interactions, authority, expertise, reputation, or familiarity. Wu et al. [10] developed a trust-based estimation method alongside a visual consensus model that provided adjustment suggestions for less contributing members, aiming to enhance the efficiency of reaching consensus. Similarly, Wu et al. [11] introduced a new consensus model that improves the level of group decision-making by offering adjustments for those not in consensus, and defined a distributed language trust decision-making space. Additionally, Liu et al. [12] leveraged trust relationships to calculate the opinion adjustment coefficients for decision-makers, thereby facilitating consensus formation. Dong et al. [13] established a model to determine decision-maker weights based on trust relationships, enabling a probabilistic linguistic method for reliably ranking alternatives in a social network. Research on the influence of empathy in group decision-making, especially within social networks, remains scarce. In GDM, empathy enables decision-makers to adopt the perspectives of others, which is crucial during various decision-making processes like voting in elections, choosing restaurants, or recommending products. Empathy is significant for understanding other group members, binding preferences and interests appropriately, and promoting orderly social development. Salehi-Abari et al. [14] proposed a social choice framework that allows decision-makers to derive utility from their own preferences and those influenced by their neighbors' empathy, translating this into a weighted classical preference aggregation. Chen et al. [15] presented an empathy-driven group decision-making model in a homogeneous network, accounting for how the empathy effect from friends or their social groups influences individual decisions. This model underscores the role of empathy in enhancing group cohesion and decision-making quality.

3. Methodologies

In order to optimize group decision-making in social networks and analyze the influencing factors, we propose a novel model method that combines Graph Neural Networks (GNN) and deep learning techniques.

3.1. Network Represents Learning and Impact Assessment

A social network can be represented as an undirected graph \( G=(V,E) \) , where \( V \) is the set of nodes and \( E \) is the set of edges. Each node \( {v_{i}} \) has an eigenvector \( {x_{i}} \) , and each edge \( ({v_{i}},{v_{j}}) \) has an eigenvector \( {e_{ij}} \) . In a graph neural network (GNN), the representation of nodes is updated by a graph convolution operation. This process can be described as being represented as \( h_{i}^{(k)} \) at layer \( k \) , where each node \( {v_{i}} \) is represented as h. The formula for the graph convolution operation update node representation is shown in Equation 1.

\( h_{i}^{(k+1)}=σ({W^{(k)}}∙h_{j}^{(k)}+{b^{(k)}})\ \ \ (1) \)

Where \( h_{i}^{(k)} \) represents the representation of node \( {v_{i}} \) at layer \( k \) . \( N(i) \) represents the set of neighbor nodes of node \( {v_{i}} \) . \( {c_{ij}} \) is the normalization constant, which is usually the number of neighbor nodes \( |N(i)| \) . \( {W^{(k)}} \) is the weight matrix of layer \( k \) . Parameter \( {b^{(k)}} \) is the bias vector of the \( k \) layer. \( σ(∙) \) is the activation function.

The representation of the current node is updated by the weighted sum of the representations of neighboring nodes, and then through linear transformations and nonlinear activation functions. Through multilayer graph convolution operations, node representations can effectively capture the complex relationship structures in social networks. The influence of each decision-maker is calculated using the node representation. Influence can be defined as the centrality of a node by applying betweenness centrality. The centrality metric helps to assess the importance of nodes in the network. Betweenness centrality measures how often a node acts as an intermediary on the shortest path between other nodes in the network, which is expressed as Equation 2.

\( BC({v_{i}})=\ \ \ (2) \)

Where \( {σ_{st}} \) is the number of shortest paths from node \( s \) to node \( t \) , \( {σ_{st}}({v_{i}}) \) is the number of shortest paths through node \( {v_{i}} \) . By calculating the centrality metrics of each node, it is possible to assess the influence of decision-makers in social networks, which is shown in Equation 3.

\( Influe({v_{i}})=Cen({v_{i}})\ \ \ (3) \)

3.2. Group Preference and Optimization Algorithms

In group decision-making, each decision-maker \( {v_{i}} \) has his or her own personal preference \( {p_{i}}(a) \) for a certain option \( a \) . In order to aggregate these individual preferences to form the overall preferences of the group, we need to consider the influence of each decision-maker in the group. If the influence of decision-maker \( {v_{i}} \) is \( Influe({v_{i}}) \) , then the group's overall preference \( P(a) \) for option \( a \) , can be calculated by a weighted average, which is shown in Equation 4.

\( P(a)=\sum _{i=1}^{n}Influe({v_{i}})∙ {p_{i}}(a)\ \ \ (4) \)

Where \( {p_{i}}(a) \) is the decision maker's \( {v_{i}} \) personal preference for option \( a \) , which can be obtained by scoring, voting, or other means. \( Influe({v_{i}}) \) is the influence of the decision-maker \( {v_{i}} \) , calculated from centrality metrics of betweenness centrality. \( P(a) \) is the overall preference of option \( a \) , which is the sum of the weighted preferences of all decision makers.

In order to optimize the decision-making process, the gradient descent algorithm can be used to search for the optimal scheme in the high-dimensional decision space. The loss function can be defined as the difference between group preference and optimal decision goals. Assuming the target preference is \( Target(a) \) , the loss function \( L \) can be defined as Equation 5.

\( L=\ \ \ (5) \)

Where \( Target(a) \) is the target preference for option \( a \) , which is usually the ideal or desired preference. \( L \) is the loss function, which represents the difference between the overall preference and the target preference.

Subsequently, by iteratively updating the parameters, the loss function is minimized to find the optimal solution. Initialize decision parameters \( θ \) randomly, the gradient for each parameter is calculated based on the loss function \( {∇_{θ}}L \) . Update the parameters according to the gradient descent method, which is shown in Equation 6. Where \( μ \) is the learning rate.

\( θ←θ-μ{∇_{θ}}L\ \ \ (6) \)

Repeat the calculation of the gradient and update the parameters until the loss function converges or reaches a preset number of iterations.

4. Experiments

4.1. Experimental Setups

In this experiment, the election dataset of the 2002 Irish general election was used as the preference information of decision-makers to learn the representation of nodes and edges in the social network, and the influence of decision-makers was evaluated through centrality indicators. The group preference is summarized by weighted average, and the gradient descent algorithm is used to optimize the decision in the high-dimensional decision space, and the loss function is defined as the difference between the group preference and the optimal decision goal. The experimental evaluation is carried out by the indicators of accuracy, decision consistency and computational efficiency, which verifies the superiority of the proposed method compared with the traditional group decision-making method.

4.2. Experimental Analysis

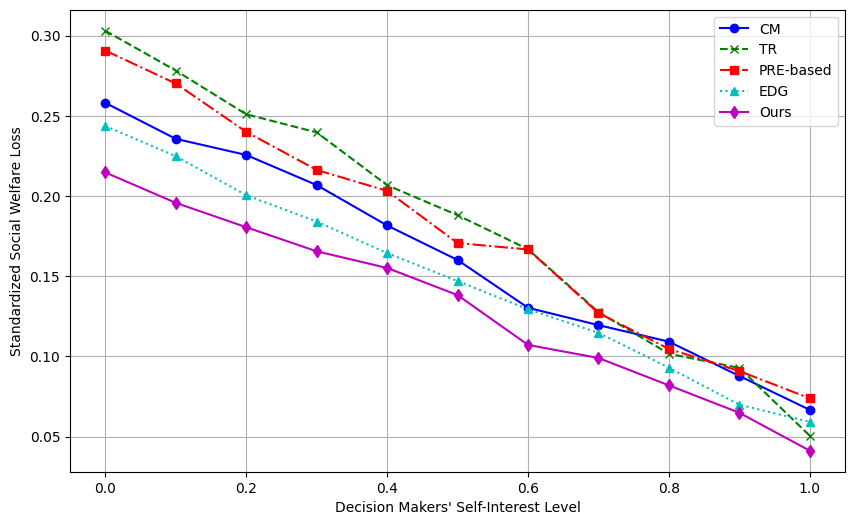
Standardized social welfare loss (NSWL) is an indicator used to evaluate the degree to which a group decision-making scheme deviates from the optimal decision-making goal, and measures the welfare loss by quantifying the difference between the actual decision-making outcome and the goal preference. Standardized social welfare losses can help to assess the quality of decision-making, compare different methods and optimize the decision-making process, and provide a unified evaluation standard through standardization. Following Figure 1 shows standardized social welfare loss results with existing methods.

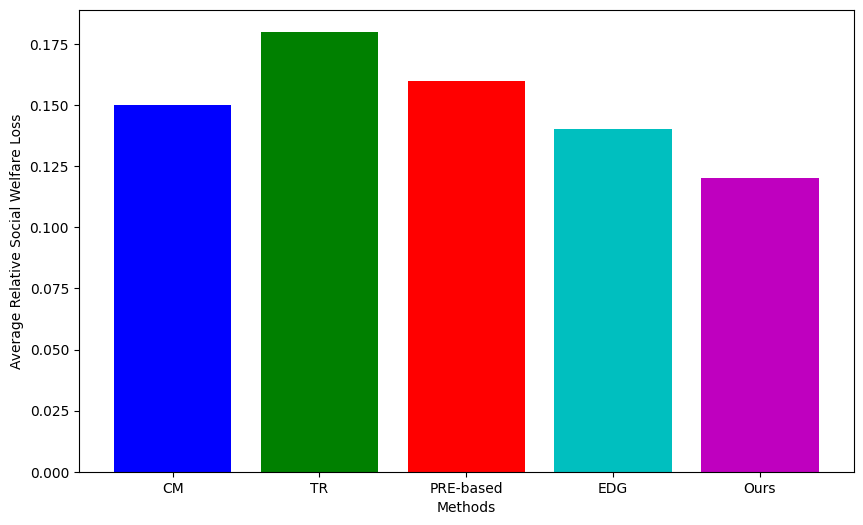
Average relative social welfare loss is an indicator used to evaluate the effectiveness of group decision-making programs, and the loss of social welfare is measured by calculating the relative deviation between the decision-making outcome and the optimal decision-making goal. Figure 2 shows average relative social welfare loss comparison results.

5. Conclusion

In conclusion, by using graph neural networks to learn the representation of nodes and edges in social networks, and evaluating the influence of decision-makers based on centrality indicators, we propose a machine learning-based method for group decision-making optimization in social networks. Experimental results show that the proposed method is superior in improving the accuracy and efficiency of decision-making, especially in terms of standardized social welfare loss and average relative social welfare loss, which is significantly better than the traditional method, which verifies its effectiveness and advantages in practical application.