1. Introduction

Credit scoring is a crucial component of the financial sector, playing a vital role in various financial operations. It involves the selection of credit customers, the assessment of risk levels, and the monitoring of loans both before and after issuance. Additionally, it is integral to comprehensive performance reviews and the management of portfolio risks. As the frequency of bank failures and significant financial losses increases, global banking regulators are pushing for the development of more refined credit risk models to effectively manage their loan portfolios. At its core, credit scoring is a binary classification challenge where loan applicants are categorized as either creditworthy or non-creditworthy based on factors like their annual income, bank account details, occupational status, marital status, age, and educational background [1]. Good credit applicants are more likely to repay their debts, while bad credit applicants are more likely to default. Credit scoring models predict whether loan applicants or existing borrowers will default or become delinquent in the future, mainly through quantitative analysis methods.

The essence of credit scoring is a binary classification problem that divides credit applicants into good and bad credit applicants according to their characteristics, such as annual income, type and balance of bank accounts, type of occupation, marital status, age and level of education. Credit applicants rated as good are more likely to pay off their debts, while those rated as bad are more likely to default. The United States was the first country to develop modern credit scoring methods and has developed a relatively mature system of personal and business credit scoring. Conventional credit scoring methods primarily utilize statistical techniques, aiming to derive the most effective linear combination of explanatory variables to model, examine, and forecast corporate default risks [2]. Nevertheless, these traditional approaches often suffer from limitations like reduced accuracy and inefficiency in handling vast datasets. As internet technologies become increasingly intertwined with the financial sector, machine learning-based credit scoring models have emerged, supplanting traditional methods due to their superior accuracy. This transition has sparked significant interest in the research community [3].

The social control and value-added nature of credit give it the dual role of stabilising market order and improving the utilisation rate of capital in market activities. However, credit risk is unavoidable in the trading process. Credit rating can provide risk information to the market, thereby strengthening the market's constraints on enterprises, so it plays an important role in the healthy development of the capital market [4]. The occurrence of credit risk is often the result of risks faced by various aspects, such as the use and repayment of loans, as well as market risks, such as changes in market interest rates and exchange rates. From the perspective of commercial banks, personal credit risk is also known as personal credit risk or personal default risk [5].

Deep learning is based on neural network structures, upon which more complex network structures are built to mimic the neural circuits of the human brain. To understand deep learning models, one must first understand the structure of neural networks. Neural networks are largely parallel, interconnected networks of adaptive, simple units organised to mimic the real-world interactions of a biological nervous system. The smallest unit in a neural network is a neuron. Each neuron in biology is connected to other neurons and, when activated, sends chemical signals to the neurons to which it is connected. When a neuron's potential exceeds a threshold, it is activated [6].

2. Related Work

The utilization of machine learning methods is increasingly recognized for enhancing the accuracy of complex credit risk analyses. Common techniques in this domain include Support Vector Machines (SVMs), Decision Trees (DTs), and Random Forests (RFs). For instance, in their exploration of SVM-based models, Huang et al [7] developed a hybrid approach to credit scoring that significantly outperformed traditional data mining techniques. In parallel, Chern et al [8] introduced a decision tree methodology tailored to navigate the complexities of large and dynamic data sets pertinent to credit regulation. Similarly, Itoo et al [9] employed Logistic Regression (LR), K-Nearest Neighbors (KNN), and Bayesian methods to assess the creditworthiness of individuals.

Recent advancements have also seen the rise of ensemble methods, which leverage multiple classifiers to enhance predictive accuracy. Zhang et al [10] crafted a novel multi-stage ensemble model that exhibits improved adaptation to outliers and has demonstrated robust performance across various real-world credit scoring datasets. Unlike traditional statistical models, machine learning approaches eschew subjective judgments, offering superior capabilities in predicting outcomes for complex, nonlinear problems—making them particularly apt for intricate personal credit assessments.

The advent of deep learning has further propelled interest in its application to credit scoring. Notably, Neagoe et al [11] have applied a Deep Convolutional Neural Network (DCNN) and a Deep Multilayer Perceptron (DMLP) to this field, while Kvamme et al [12] utilized CNNs to analyze consumer transaction data for mortgage default predictions. Additionally, Dastile et al [13] developed an interpretable deep learning model for credit scoring, underlining the potent efficacy of DCNNs in this area, albeit noting the challenges posed by their complex structures and the substantial data requirements for effective training. These advancements underscore a shift towards more sophisticated, data-driven models in financial assessments.

3. Methodologies

Personal credit scoring models are based on deep learning and aim to improve the accuracy of credit scoring using large amounts of data. The model mainly uses deep neural networks (DNNs) and combines a variety of input features, including the user's transaction history, social behaviour and other relevant data.

3.1. Notions

To begin with, the main parameters are summarised in Table 1 below.

3.2. Deep Neural Network

A neural network consists of several layers, including an input layer, a hidden layer and an output layer. The nodes in each layer are connected by weights and non-linearly transformed by activation functions. The following points describe the structure of a neural network.

• The input layer accepts raw data input. The input data is a vector \( x \) with a dimension \( n \) . Each node of the input layer corresponds to an element of the input vector.

• Hidden layers are responsible for extracting and transforming features, and the nodes of each hidden layer are connected to the nodes of the previous layer through weights and offsets. For a given input vector \( x \) , the hidden layer node is computed as follows Equation 1.

\( {h_{j}}=σ(\sum _{i}{w_{ji}}{x_{i}}+{b_{j}})\ \ \ (1) \)

Where \( {h_{j}} \) is the output of the hidden layer node \( j \) . Function \( σ(∙) \) is the activation function, and \( {w_{ji}} \) is the weight of the connecting input node \( {x_{i}} \) and the hidden layer node \( {h_{j}} \) . Parameter \( {b_{j}} \) is the bias of the hidden layer node \( j \) . The purpose of the activation function \( σ(∙) \) is to introduce nonlinearity, allowing the neural network to handle complex nonlinear problems.

• The number of nodes in the output layer is contingent upon the specific task at hand. In a binary classification problem, the output layer typically comprises a single node, with the classification probability determined by the activation function. In a multi-classification problem, the number of nodes in the output layer is equal to the number of categories. The probability of each class is calculated by the softmax activation function.

Additionally, we utilize the deep neural network with multiple layers, the layer-to-layer computation can be expressed as Equation 2.

\( {a^{(l+1)}}=σ({W^{(l)}}{a^{(l)}}+{b^{(l)}})\ \ \ (2) \)

Where \( {a^{(l)}} \) is the activation value of layer \( l \) and the output of layer \( l \) nodes. \( {W^{(l)}} \) is the weight matrix of the layer \( l \) . \( {b^{(l)}} \) is the bias vector of layer \( l \) .

The activation value \( {a^{(l)}} \) of each layer is calculated by the activation function after the output of the previous layer is linearly transformed by the weight matrix and bias vector. This process is repeated at each layer of the network until the output layer produces the final prediction.

3.3. Back Propagation and Optimization

Backpropagation refers to the process of computational of gradients from the output layer to the input layer to update the weights and biases of the network. The gradient of the calculated loss function \( L \) is expressed as Equation 3.

\( ∇=\frac{dL}{d{W^{(l)}}}+\frac{dL}{d{b^{(l)}}}\ \ \ (3) \)

Following Equation 4 updates weights and biases.

\( {W^{(l)}}={W^{(l)}}-μ\frac{dL}{d{W^{(l)}}}, {b^{(l)}}={b^{(l)}}-μ\frac{dL}{d{b^{(l)}}}\ \ \ (4) \)

Where \( μ \) is the learning rate. Through the above steps, the neural network can gradually optimize its parameters and improve the prediction accuracy.

The goal of the model is to minimize the error between the predicted and true values. For classification problems, the cross-entropy loss function is defined as Equation 5.

\( L=-\frac{1}{N}\sum _{i=1}^{N}[{y_{i}}log{({\widetilde{y}_{i}})}+(1-{y_{i}})log⁡(1-{\widetilde{y}_{i}})]\ \ \ (5) \) where \( N \) is the sample size, \( {y_{i}} \) is the true label, and \( {\widetilde{y}_{i}} \) is the predicted probability. Use gradient descent to update the weights and biases of the network.

4. Experiments

4.1. Experimental Setups

To test the performance of the advanced algorithm introduced in this study, we utilized two prominent datasets: the Australian Credit dataset and the Default of Credit Card Clients dataset. Preliminary steps in our experimentation included data preprocessing, which encompassed filling missing values, normalizing data, and encoding categories. We implemented a Deep Neural Network (DNN) as our model framework, which consists of several fully connected layers equipped with suitable activation functions. During the training phase, we utilized the binary cross-entropy loss function and the Adam optimizer, setting the training to 100 epochs and batch size to 32 records. Our evaluation metrics were accuracy, precision, recall, and F1-score, and we enhanced the model's robustness through 5-fold cross-validation.

The Australian Credit dataset, sourced from the UCI machine learning repository, includes 690 entries with 14 attributes each, typically used for binary classification tasks. Attributes of this dataset include age, gender, income, credit history, loan amount, and repayment history, making it a benchmark dataset in credit scoring and risk prediction. On the other hand, the Default of Credit Card Clients dataset contains 30,000 entries, each with 24 attributes, and is designed to predict defaulting behaviors among credit card holders. Key attributes include credit limits, gender, educational background, marital status, age, and financial behaviors over the previous 24 months, such as bill amounts and payments. This dataset is invaluable for researching sophisticated credit scoring models due to its extensive customer data and detailed historical records.

4.2. Experimental Analysis

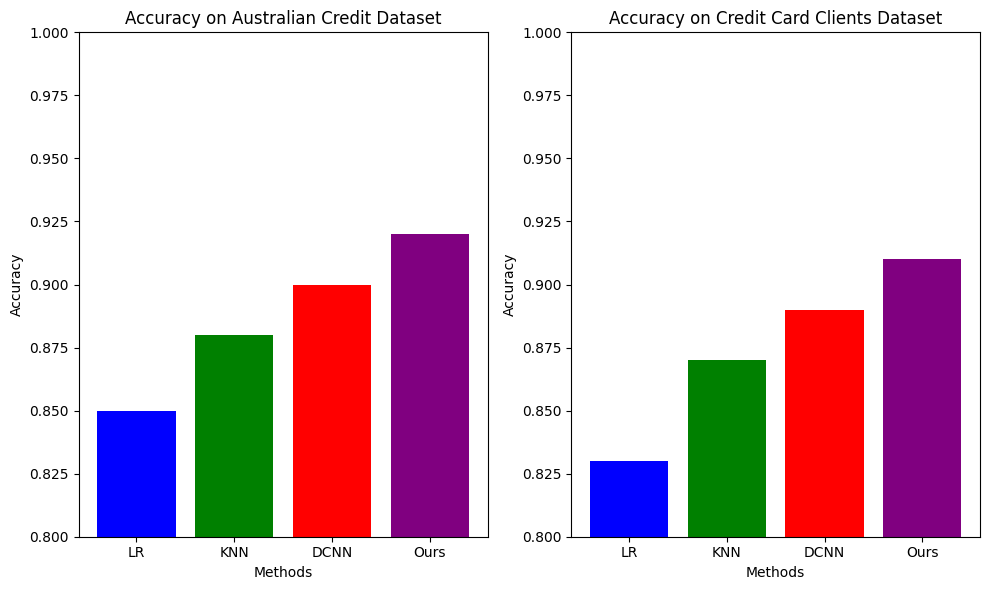
Accuracy is a frequently employed metric in the assessment of classification models, signifying the ratio of correctly predicted samples to the total number of samples. Accuracy gauges the comprehensive predictive precision of the model, representing the extent to which the model's predictions are accurate. However, in the context of datasets characterised by imbalanced categories, relying solely on accuracy may yield misleading outcomes. As illustrated in Figure 1, the scoring results with existing methods are presented.

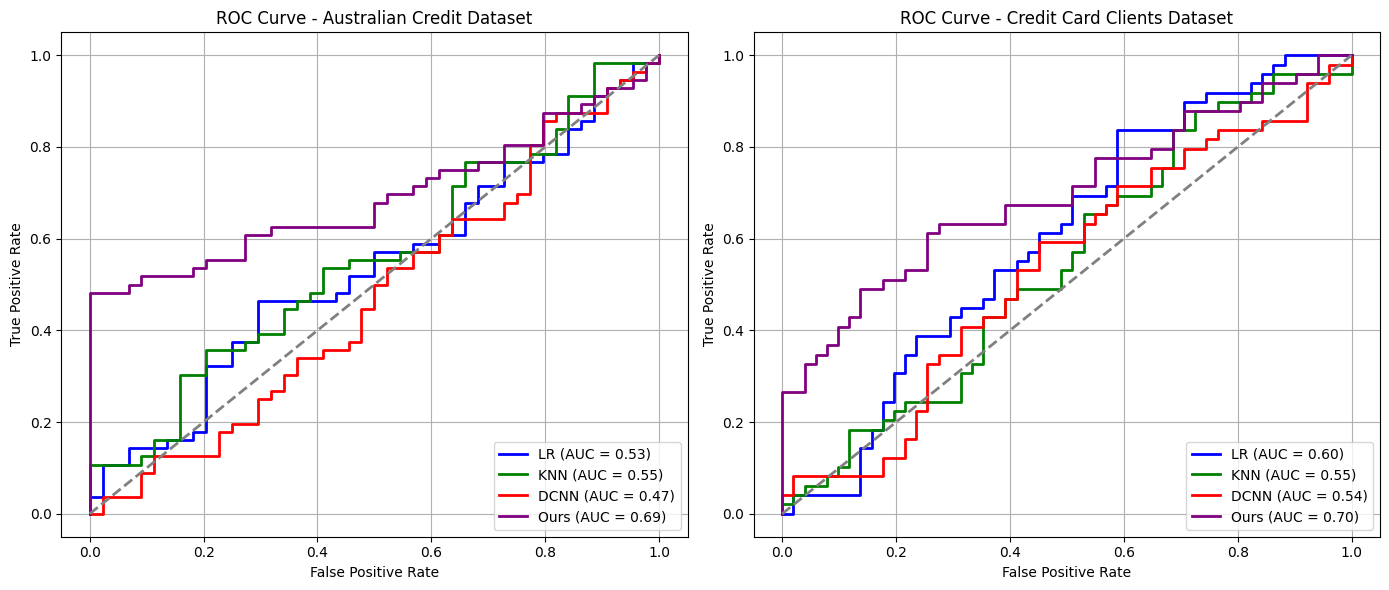
The Roque curve (Resif, Opatincharat, Charaktrichkov) is a tool to evaluate the performance of a classification model, measuring the classification ability of a model by demonstrating the relationship between the true positive rate (Truposti Tivrat, Tepper) and the false positive rate (Fars Postivrat, Vorper) at different thresholds. The area below the Rock curve (Oak, Aryaendekov) is an important indicator of the overall performance of the model, and the larger the Oak value, the better the classification performance of the model. The Roque curve and Oak value can intuitively reflect the effect of the model in processing positive and negative sample classification, which is especially suitable for model evaluation of unbalanced datasets. Figure 2 shows the ROC curve comparison results.

5. Conclusion

In conclusion, the personal credit scoring model based on deep learning improves the accuracy and robustness of credit evaluation by employing deep neural networks (DNNs) and rich data features. Experimental results show that the proposed model is superior to the traditional LR, KNN and DCNN methods on both the Australian Credit dataset and The Default of Credit Card Clients dataset, and shows higher AUC values and better classification performance. This proves the potential of deep learning in complex nonlinear systems, especially in the field of credit risk assessment, to provide financial institutions with more reliable decision support tools.