1 Introduction

Cybersecurity is concerned mainly with ensuring the confidentiality, integrity and availability of digital data that is either stored, sent or received by the use of diverse security principles, protocols, and measures. With the ubiquitousness of computing and the corresponding information technology revolution, an unparalleled progression has been witnessed continuously in the number of cyber-attacks and their corresponding impact in terms of monetary damages, reputation and data theft. Also visible is a growing trend in the newer forms of attacks with complexity, stealth, scale, tenacity, and strategic penetration.

The control over the computer and the IT systems is literarily a cyber-battle between the cybercriminal and the cyber-defender. Whereas the defender is persistently expending effort to exercise firm control over the computer at all times, the attacker is concerned with wrestling away and exercising illegitimate control over the entire computing process [1].

Cyber-attacks are often prosecuted through digital weapons that are often indiscernible to human cognition. These attacks are neither limited by geographic nor by ideological boundaries; and they require highly sophisticated and technical know-how. Most especially, they could be highly dynamic and widely distributed. Hence, a defender in the cyber world may need strategies that are dynamic and strategic for sophisticated attackers.

Several mathematical models have been proffered and used in the academia and industry to model and analyze the decision-making problems and processes in security. For example, Decision Theory (which is the classical mathematical tool to study decision problems), Control Learning, and Machine Learning [2]. In addition, Probability theory, utility theory, decision analysis and their subfields have developed tools and mechanisms for understanding and assisting decision making in environments with tendencies toward probabilistic risk [3]. However, Game Theory has gained prominence to study cybersecurity problems since it captures the adversarial nature of the cyber conflict and provides principled way to frame modern security challenges.

2 Game Theory

Game theory is the name given to the methodology of using mathematical tools to model, analyze, and understand situations of interactive decision making among independent, self-interested agents which could be any of conflict, cooperation, and coordination [4]. It aims at equilibria, situations in which no participant would abandon his strategy, if one else does it as he would lose. Game theory was introduced into the security domain to confront strategic human adversaries and to proffer quantitative insights and solutions in security management [5][6][7].

2.1 Components of a game

The essential elements of a game are: the players, actions, strategies, payoff functions, and an equilibrium [8][9].

Players are the persons, systems, institutions or entities making their own independent decisions, with a bias toward personal selfish goals and preferences. Other entities or players could be nations, organizations, animals, computing systems etc. It is assumed that each entity is rational with an objective or end goal to maximize his utility. Utility here, refers to the measure of happiness, gratification or satisfaction derived from a behavior. Utility theory has become the central approach to model an agent’s interests as it quantifies the agent’s degree of preference when faced with multiple choices and alternatives.

Actions are the decisions made by each player and each player is presumed to have perfect information concerning the possible choice or actions to be taken by other players.

Payoff refers to the concept that describes or quantifies the satisfaction that a player derives from taking an action. At the end of each game, the payoff is often made known.

Strategy is a player’s set of actions a player has in mind to respond to past and expected set of actions of other players. A pure strategy is an unconditional and defined choice that a player makes.

Equilibrium of a game refers to a set of mixed strategies (a group of randomized pure strategies), one for each player, a condition in which a player will continue with his initial strategy, with no incentive to deviate from it whatsoever, after taking into consideration the opponent's strategy. John Nash proposed the Nash equilibrium in the 1950s and was able to conclude that with each normal-form game, there is a corresponding Nash equilibrium [10].

2.2 Representing Games

Games are usually represented as normal-form and extensive form.

The normal-form is the best-known representation scheme for games (also referred to as the strategic form, or, the bi-matrix form, in the case of two players).

The extensive-form games allow modeling of the temporal and informational structure of a game. Shows the sequential order of decisions and actions.

Every game written in the normal-form represents the description of every player’s utility for every state of the world, especially in cases where the states depend only on the players’ joint actions.

For example, if the strategy profile for an N player game in a network security game is represented by:

\( { a_{1}}, {a_{2}},{a_{3}},…a_{N}^{*} \) (1)

where \( a_{N}^{*} \) is the Nash equilibrium, if each player \( i, \) has payoff of \( {U_{i}} \) then

\( { U_{i}}(a_{i}^{*}, a_{-1}^{*})≥{U_{i}}(a_{i}^{*}, a_{-1}^{*}) \) (2)

has to be established for each player \( i \) where \( a_{i}^{*} \) is the action profile of player \( i \) and \( a_{-1}^{*} \) is the equilibrium action of all other players.

A normal-form game \( A \) , can be represented by a tuple \( (N, A, u), \) where

\( N \) is a finite set of \( n \) players, indexed by \( i \) ;

\( A={A_{1}}×…× {A_{n}}, \) where \( {A_{1}} \) is a finite set of actions available to player \( i. \) Each vector

\( a= \) ( \( {a_{1}},…, {a_{n}} \) ) \( ∈ A \) is called an action profile;

\( u= \) ( \( {u_{1}},…, {u_{n}} \) ) where \( {u_{i}}:A⟼R \) is a real-valued utility or payoff function for player \( i \) .

The usual approach of representing games is often through an n-dimensional matrix. Consider the Transmission Control Protocol (TCP) user’s game in Fig. 1. Two colleagues, Kim and Sasha are the only people using the internet during late hours of the University. Internet packet-streaming and traffic is regulated by the TCP protocol that has a feature, backward mechanism to regulate the rates at which packets are sent into the network by users and thus avoid congestion.

A correct implementation requires that whenever Kim and Sasha release information packets into the network, and it causes congestion as a result of the unrestricted rates, each one of the two backs off and reduces the rate for a while until the congestion abates. Both colleagues are presented with two strategies \( C \) for using a correct implementation, and \( D \) for using a defective one. If both Kim and Sasha choose option \( C \) (a correct implementation), then their individual packet delay is 1 ms. However, if they both implement \( D \) (a defective implementation), then their average packet delay is 3 ms.

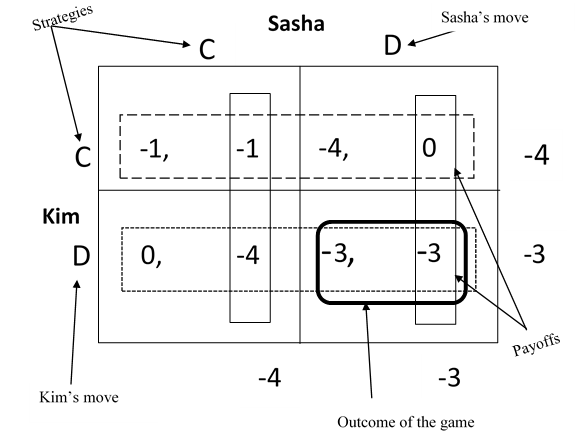
Fig. 1. The TCP packet regulating game (or the Prisoner’s Dilemma).

Kim is the row player, while Sasha plays from the columns. The first number in each cell signifies Kim’s payoff (or, the negative of her delay) and the second number represents Sasha’s payoff (or, the negative of her delay).

This is an example of the unique situation known as the prisoner’s dilemma. Kim and Sasha are better off if they both agree and choose strategy (C, C), that is the option (-1, -1) as it represents the least regular packet delay of 1 ms for the two. However, if the network operator forbids the two from communicating with each other, both colleagues will choose the option (D, D), that is (-3, -3) as it maximizes their expected utility as a result of information asymmetry between the two of them. Option (-3, -3) represents a delay of 3 ms. Notwithstanding, the two colleagues, uncertain of what the strategy the other person is scheming for, will settle for the strategy that yields her minimum packet delay irrespective of what her colleague chooses.

This is called the Nash equilibrium and it is the solution for the game. Thus option or strategy (D, D) is referred to as the dominant strategy or equilibrium of the game since it gives either player a larger payoff than any other, irrespective of what the other party chooses.

3 Classification of Games

Games are of several kinds, however, they are mainly classified into three categories of games of skill, games of chance, and games of strategy depending on the perspective [11]. Games of strategy are particularly applicable in cybersecurity. Fig. 2 shows the classification of game models applied to cybersecurity and their security concerns [12]. The two major categories of game theory and application in cyber security are in the cyber attack-defense analysis and in cyber security risk assessment [13]. Through modeling the defense and attacker’s actions as games, the attacker’s actions can be accurately predicted and the optimal defense move can be computed accordingly. The final equilibrium state of the game can then be used as the foundation of cyber security policies and valuation.

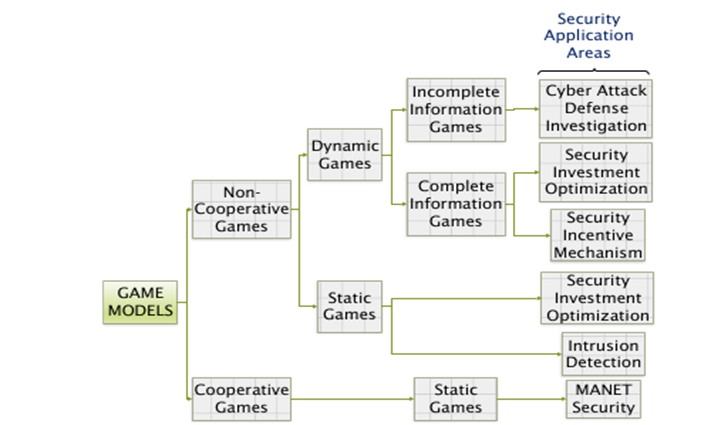
Fig. 2. A classification of game models.

3.1 Definitions and Classifications of games

Cooperative game theory aims to determine what people get when they are in a coalition(s) that tries to improve participant’s collective welfare. As a result, decision-makers or players can make a binding agreement to enforce some action on one another.

Non-cooperative game, on the other hand is the tool used for analyzing interactions in strategic interdependence. Non-cooperative game theory aims to find out what happens in a strategy combination or in a society when the players make independent and strategic decisions. Thus, decision-makers or players cannot make a binding agreement to enforce some action on one another. Many cyber security challenges and scenarios in reality are classified as non-cooperative games.

A static, or otherwise strategic game is a one-shot game whereby each player chooses his plan of strategy and all the decisions made by the opposing players are simultaneous. In such a game, players are ignorant of their opponent’s behavior.

Dynamic games or extensive games in contrast to static games are games in which players move sequentially and not all-together, for example, extensive-form games. Players in this mode often have some information pertaining to the behavior of their opponent; the execution of the game is carried out in series of steps.

A Complete information game describes a scenario where all the players involved in the game are privileged to have complete knowledge of their opponents’ behaviors and their strategies.

An Incomplete information game on the other hand refers to a scenario where any one of the set of players participating in the game will have no information concerning the opponents. This results in a player not been able to make perfect strategy to win the game.

A Perfect Information game describes a game in which each player knows all the previous actions of their opponent before making his own move.

An Imperfect information game refers to at least one player who is not privileged to know the past moves of his opponent. As a result of lack of perfect information concerning opponent’s moves, decision making and counter moves are often difficult. Most games in cyber security are classified as games of imperfect information.

Repeated games are iterative and extensive games with perfect information and simultaneous moves in which a history is a sequence of action in the game. Often, they are either finitely repeated or infinitely repeated.

Stochastic game is a version of repeated game where the state changes from one state to another according to a transition that is dependent on the current state and the moves of both players.

Zero-Sum games are non-cooperative games between two players in which one is a maximizer and the other a minimizer. The gain by the maximizer is from the loss of the minimizer.

Non-zero sum games on the other hand are types of game played by multiple players, and the summation of the payoff values of the players is dynamic throughout the game. All the players have the objectives of maximizing or minimizing without having any constraints on the overall payoff value as is the case with zero-sum games.

Stackelberg games, often referred to as the leader-follower game are used for modeling two competing actors where one of the actors is the leader of the game who chooses an action from a specific set \( {A_{1}}, \) and the other player, the follower observes the previous action and responds accordingly by choosing from a different set \( {A_{2}} \) [14].

3.2 Evolutionary Games

Evolutionary games was developed in Biology to model evolving and dynamic groups of players having a distribution of strategies. Classical game theory offers a fixed approach to recognizing Nash equilibria and the accompanying utilities for players in a game. It has limitations in a real-world scenario. To overcome this limitation, evolutionary game theory was developed since it can model evolving populations of players having a distribution of strategies. Unlike traditional game theory models, however, the payoffs for evolutionary game are often interpreted as corresponding to fitness [15]. Thus, evolutionary game theory has to do more with survival of the fittest; and natural selection replaces rational behavior (a major basic assumptions of traditional game theory). Evolutionary game theory refines the notion of a Nash Equilibrium to an evolving equilibrium by introducing the Evolutionary Stable Strategy (ESS) notion that is sufficient to thwart modified strategies.

3.3 Behavioral Games

Behavioral game models enables the modeling of strategic antecedents of intelligent adversaries and equips the defender with insights of their most likely actions and how to counter them. Social motives do often occur in strategic situations such as altruism, fairness, trust, vengeance, hatred, reciprocity and spite, and when they do, behavioral game theory is often the preferred choice of analysis [16].

Traditional game theory assumes players to be rational. However, behavioral economists have proved otherwise. Behavioral game theory slightly deviates from the game theory assumption of perfect rationality by taking irrational factors into consideration and thus makes a game model more socialized. In it, human behavior is not motivated solely by gain, it is also shaped by complex ideas like fairness, injustice, and even revenge. One common feature in behavioral game theory is the demand on individuals to learn about their opponents’ strategies through direct and repeated feedback.

3.4 Signal Games

Signals are actions that more informed players use to convey information to less informed players about the unobservable type of the more informed player.

Signal games are an important dynamic games of incomplete information [17] with a two-stage game, where a first player (with private information) moves first and this move is observed by a second player. Inadvertently, the second player (with no knowledge of the first player’s private information) moves second; then the payoffs are realized.

Games with incomplete information can be categorized by a preceding move by nature which is unobserved by at least one player. When nature moves, it is often done randomly, and this often determines the game structure or the types of players.

3.5 Differential Games

Differential games lies at the intersection of game theory and control theory and it is used in addressing optimal control problems. They model strategic interactions between two or more agents that control the evolution of a system over time [18]. Differential game theory studies conflict situations in systems driven by differential equations. It is a kind of cooperative where players interact with each other continuously to achieve their own optimal objectives.

4 Game theoretic models review in Cyber Security

Cyber-security can be modelled mathematically as a conflict between two types of agents: the attackers and the defenders. Thus, cyber security scenarios are classified as the non-cooperative dynamic game model and structure.

The authors in [19] proposed a novel approach that models cyber security in terms of signaling games involving transfer of an app from a sender (an app store) to a receiver (an app receiver). Because of the information asymmetry, it is possible for the sender to be deceptive, as is often in cyber scenarios. Pawlick and Zhu [20] investigated a model of signaling games, cheap talk in which the receiver can detect deception with some probability. Feng, Zheng, Cansever, Swami and Mohapatra [21] showed that the defender, who has the objective of protecting a critical resource across a network of nodes, may exploit the uncertainty created by moving target defense (MTD) through the use of a signal game to adjust the attacker’s behavior for its own benefit.

Tosh, Sengupta, Kamhoua, Kwiat & Martin [22] propose evolutionary game theoretic framework for Cyber Threat Intelligence sharing to determine suitable conditions under which a player’s stability can be attained. Also, the authors in [23] present one of the most recent economic studies on Cybersecurity Information Sharing (CIS) using evolutionary game theory between organizations, and analyze Information sharing advantages. The authors in [24] used evolutionary game to study Advanced Persistent Threats (APTs) that symbolize stealthy, potent, lasting, and well-financed attacks against cyber facilities, such as smart grids, data centers and cloud storage. Bouhaddi, Adi & Radjef [25] use evolutionary game theory to investigate the optimal behavior of the ad-hoc network nodes in the presence of malicious actors.

The authors in [26] used a two-layer differential game in an open-loop setting to examine the dual threats from the Advanced Persistent Threat, APT attacker and insiders over an extensive time-span within a general framework in which insiders are prone to be exploited for the APT attacks through information-trading. While the authors in [27] used a differential game model to obtain two possible closed-loop Nash equilibrium solutions in an interaction between the botnet herder and the defender group comprising of network and computer users.

4.1 Cyber Security and the Insider Threat

In typical conventional battlefields, human beings face one another in deathly combat, however, the cyber battlefield is different, it is synthetic, i.e., not naturally found, and highly mutable. All of the components in the cyber battlefield are man-made. Hence, it follows that the components and the cyber battlefield may be equally altered by human beings [1].

Until recently, much of cyber security has focused on external perimeter defense against threats such as unauthorized access to networks, denial of service attacks, viruses, Trojan Horse attacks, Worms, etc. However, the greatest threat to computer systems and their information comes from humans, often referred to as the weakest link in the cybersecurity chain through actions that are either malicious or ignorant [28]. When the action is malicious, some motivation or goal is generally behind the attack. This is known as the insider threat and is more destructive than outsider attacks. Insider threat describes malicious actions that cause harm to an organization’s computing systems and network facilities, applications, or services on the part of a trusted employee who has legitimate access to the organization’s information assets [29].

Insider threats can have a profound impact on an organization. The impact can range from financial loss, loss of reputation, loss of competitive advantage, and prolonged impacts on organizational goals.

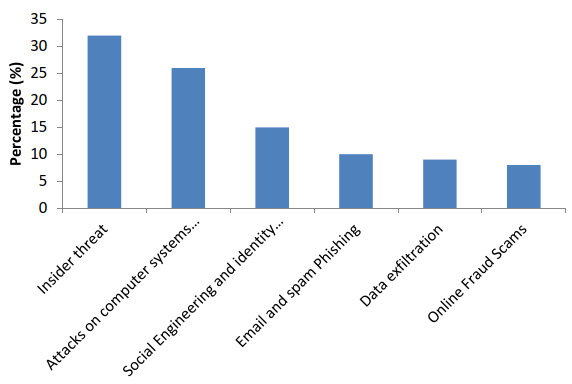
Fig. 3. Distribution of the cyber-attacks cost per type of attacks in 2016 in Africa

From Fig. 3 above, Tambo and Adama [30] showed the distribution of the cyber-attacks cost per type in Africa in 2016. This clearly shows that the insider threat is the biggest security concern in most African organizations and closely followed by attacks on computers, social engineering and utility theft.

Human threat is often associated with the factors of motivation, opportunity, and capability. Thus, these factors ought to be included in insider threat assessment. Most practical and procedural measures are available that can be used for quantifying opportunity and capability, but tackling motivation is often very challenging.

Many game-theoretic models have been proposed for detection and mitigation of the insider, however, most of the works have assumed a risk-neutrality status on the part of the attacker [28][31][32]. A decision maker in a risky situation can be either risk averse, risk seeking (or risk loving), or risk neutral.

5 Future Research and Conclusion

Popular and widely-used game-theoretic models of competition most usually, and very often ignore risk preferences and attitudes toward risk by assuming that players, when faced with uncertainty, are risk neutral. With this assumption of risk neutrality, the utility functions are therefore linear in the payoffs accordingly. Thus, according to the expected utility theory (the major model for investigating risk preference or attitude) a player’s equilibrium behavior may be altered [33]. In reality, decision-makers could be either risk loving or risk averse, which has not been given much attention extensively in most of the attacker-defender game literature.

Generally, risk neutrality is supposedly appealing theoretically, and often computationally convenient. However, it is a well-established fact that when individuals are faced with situations involving uncertainty, they often deviate from risk neutrality and exhibit varying degrees of risk aversion. For example, a malicious insider with the intent of data theft of Intellectual Property is aware of the likelihood of failure and the penalties associated with being apprehended [34]. In framing his decisions, the model should incorporate his risk-perception in order to arrive at a more reliable Nash equilibrium since the risk-averseness directly shapes his utility function [35].

When defenders understand the dynamic processes, the decision making processes of insiders, and their attitudes toward risk, they can use that knowledge to choose among alternatives that have different uncertainties with risks and benefits. The performance of an optimal defense strategy critically depends on how accurately the attackers’ responses are predicted. Thus, there is a growing need to integrate human factors discipline with behavioral cybersecurity.