1. Introduction

Traffic route and transportation are important points in any city planning [1,2]. MST is a way to find the best path, and Kruskal’s algorithm is one of the ways to make the MST. In a graph, assume the weight of the edges between the vertexes is time or cost, not just geographical distances. Kruskal’s algorithm provide the shortest path. Thus, many researchers are working on transportation and traffic problems by Kruskal’s algorithm.

Recently, Dutta et al. developed the open vehicle routing problem, and proposed a new Kruskal’s algorithm [3]. Rani and Owais mentioned that use Kruskal’s algorithm to get the flow of air traffic [4]. Hu, Dong, and Xu show a way to use Kruskal’s algorithm to plan the path of underground logistics system network for parcel delivery, automated construction, demolition, waste collection [5].

However, the application of MST in bus route planning and how to solve the impact of different factors on traffic research, such as weather, road condition, and time did not be solved.

Thus, in this paper, the classical Kruskal’s algorithm will be consider to application on bus route plan, and how to include the several factors to improve the accuracy of the route. In the real environment, the time to arrive target or choose the route is influenced by many factors. Driver will decrease the speed at rain day; be careful on a bad road section; get stuck in traffic during rush hour. Those factors will be considered to plan the route.

This paper researched base on Kruskal’s algorithm, and include the different factors to change the weight of edges between the vertexes.

This research will help us to plan the bus route to improve the efficiency with when people are traveling. On the other hand, it can help us improve the environment. Bus is one of the public traffic. If the efficiency of bus improved, more people tend to take bus and less people drive the private car. It will cause that greenhouse gas emissions are reduced.

2. Preliminaries

2.1. Kruskal’sAlgorithm Steps

Kruskal's algorithm appeared in 1956 and was first proposed by Joseph Kruskal. Loberman & Weinberger rediscovered it in 1957 [6,7].

Consider anundirected graph G(V, E) which V is a set of vertexes V = {1, 2, 3 …}and E is a set of edges (i, j), where i, j ∈ V.

Kruskal’s algorithm has 3 steps: firstly, sorted all edges by weight.

Secondly, choose the lowest weight and check to see if it makes a cycle with the tree already formed. If it did, discard it. Oppositely, include it in the tree.

Finally, repeat the second step to get all vertexes. In another word, get V-1 edges.

2.2. Pseudocode

Kruskal_function(G, w): //G is graph, wis weight

1 S={} // create an empty set to keep final MST

2 for each vertexes in G

3 create a new set V

4 sort edges by ascending order

5 for each edges (i, j) in ascending order by weight: // number of edges is (V-1)

6 choose the lowest weight edges

7 if this edge does not create a cycle with exist tree:

8 add the edge to S //use union and find function, log(E) runtime in theory

9 increment the index to move to next edge

10 return S // return final MST created

3. Proposed Method

In the real environment, we need to consider how these external influences affect our trip. Put it in the algorithm, it is that how weight was influenced by these factors. Thus, the Kruskal's algorithm does not need to change. Before the sort, consider the external factors to change all weight of edges. Then, use the changed edges weight to do Kruskal's algorithm like the pseudocode 2.2. Finally, the result is the path but route researchers need.

This research will find the data and factors from past journals to do the forecast of influence. In this paper, the weather, and road condition are considered primarily.

3.1. Weather

Table 1. Rain Division.

Table 2. Snow Division.

Table 3. Fog Division.

To avoid the accident, a part of driver will slow down when they are on the road [8,9]. According to the Zhao et al., the severe weather will obstruct the driver's view. In rainy days, the windows will be covered with water droplets; in snowy days, the windows will be covered with snow particles and reduce ground friction coefficient at same time; and in foggy days, the vision will be directly reduced [9].

In the rain day, the light rain will decrease 2% - 4% speed of vehicles, the heavy rain will decrease 4% - 7% speed of vehicles.

In the snow day, the light snow will reduce 3% - 5% speed of vehicles, the heavy snow will reduce 30% - 40% speed of vehicles.

In the foggy day, Light fog hardly reduces driving speed, but dense fog reduces driving speed by 25%-30%.

3.2. Road Condition

Jägerbrand and Sjöbergh supported that the driving speed will be influenced by road light [10]. For the road without road light, there are almost no difference between the daylight and dark for driving speed. However, if the road did not hold the road lights, the driving speed at rain day and snow day will decrease 1.4% and 3.8% especially. Nevertheless, they did not do the research of foggy day, but foggy day can be assumed no influenced. Because the foggy and dark are both decrease the visibility directly. Even if there was light, it was useless in thick fog.

4. Transportation and Traffic Network Application

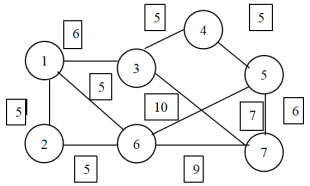
Figure 1. A traffic routes example.

In the graph, assumed the weight is time which run in common condition between two vertexes. The weight of edge between 5 and 6 is 10, weight of edge between 3 and 7 is 7.

In this section, the MST will be built by Kruskal's algorithm which base on change weight with weather and road condition. The classical Kruskal's algorithm will be run after the weight change by weather and road condition.

There are three conditions that we use these factors to get closer to the real environment.

4.1. Base on Weather

In the most of time, the rain or snow or fog will cover whole city. Thus, the weather will change all weight of edges. For example, in the heavy snow day, assumed the speed of the vehicles will reduce 30%. Because other elements remain the same, only speed was changed. The changed weight is original weight divided by (1-30%).

In this step, the final MST will not be changed. Because the default snowfall will cover the whole city, so all the weights will be changed. If all weights were changed, the order of weights after change will not change, too. The order should be (1-2, 7.14), (1-6, 7.14), (2-6, 7.14), (3-4, 7.14), (4-5, 7.14), (1-3, 8.57), (5-7, 8.57), (3-7, 10), (6-7, 12.86), (5-6, 14,29). If run Kruskal's algorithm after this step, the MST will be (1-2), (1-6), (3-4), (4-5), (1-3), (5-7).

Table 4. The Weight change in Snow Day.

4.2. Base on Lighting

According to the Jägerbrand and Sjöbergh, the driving speed will be changed by lighting condition at night in bad weather. Specifically, at night of snow day, the driving speed will decrease 3.8%, if there are no road lighting [10]. Assumed that edges 1-2, 5-7, 6-7 did not hold the road lighting, the weights of these edges will be divided by (1-3.8%).

Table 5. The Weight change in Snow Day.

In this step, the researcher got the weight at night of snow day. After these weights were ordered, the Kruskal's algorithm can be ran by them. The order is (1-6, 7.14), (2-6, 7.14), (3-4, 7,14), (4-5, 7.14), (1-2, 7.42), (1-3, 8.57), (5-7, 8.91), (3-7, 10), (6-7, 13.37), (5-6, 14.29). Finally, if we run the Kruskal's algorithm here, we can get (1-6), (2-6), (3-4), (4-5), (1-3), (5-7). Compare with the route from snow daytime, the (1-2) became (2-6). The weight of night weight of (1-2) is 7.42. It is bigger than weight of (2-6) 7.14. Thus, the preference improved. Thus, we can use the first route at daytime, and use the second route at night.

On the other hand, there are other two ways to apply the external factors. First, the weights are changed according to the most common weather in the local climate. Second, according to the weather changes of the day, different routes can be updated every day.

5. Conclusion

In this paper, the weights required by the Kruskal's algorithm are processed and reordered in advance through the collected data, so as to bring the best path obtained to real life. Two key factors were addressed: weather and road lighting. By comparing the changed path with the original path, we can see that taking into account the weather and road lighting will change the final path and actually improve the optimal path in real life. This method can be applied not only to bus routes, but also to all general car route planning (navigation), where the effects of weather and road lighting are taken into account, as well as transportation (long distance). Even because long-distance travel will pass through

different regions, it is impossible to have the same weather all the way, the weather will also change the final ordering of the weights and the final path.

However, this is not mean that this method is perfect. There are more factors need to consider in the real world, such as quality of road, width of road, and rush hours. In the future, if enough data can be collected and connected to the Internet and the Climate Bureau, even real-time route changes can be achieved.

Acknowledgment

The author thanks anonymous and their valuable suggestions. The Greg Silber from University of Delaware and Venkatesan Guruswami from UC Berkeley teaches the basics of the algorithm.