Federated machine learning in finance: A systematic review on technical architecture and financial applications

Ruixin Kang; Qihui Li; Haodong Lu

doi:10.54254/2755-2721/102/20241017

1. Introduction

In recent years, the growth in the number of customers in the financial industry, coupled with the diversification of services and advancements in technology, has led financial institutions to adopt modern computer technology to complement traditional manual methods [1]. The significant advancements in machine learning have made it widely used in the financial industry and achieved good results [2]. To obtain a high-performance machine learning model, a large amount of data is often required for training [3]. However, in real life, data usually exists in the form of 'data islands' [4], and it is difficult for engineers to obtain enough data directly from a single data source. The traditional approach involves centralized learning, where data from various sources is aggregated onto a single server for model training [5]. However, data leakage can occur during the data transmission process. Customer data stored in financial institutions is sensitive and private. Such leakage can have significant negative impacts on both financial institutions and their customers. Therefore, this data should remain within local financial institutions. Additionally, the introduction of the General Data Protection Regulation (GDPR) [6] also emphasizes the importance of privacy protection when sharing data across different sources. Therefore, aggregating customer data stored by various financial institutions to train a high-performance machine learning model while ensuring data security is a critical and practical challenge in real-world scenarios.

Federated Learning (FL) is a technique for training machine learning models on distributed datasets [7]. FL enables data to remain on local computer for model training, eliminating the need to transfer data to a central server. The FL process is illustrated in Figure 1. Different local computers \( C_i \) use locally stored data \( D_i \) to train sub-models \( M_i \) , which are uploaded to central server \( S \) for integration. The server \( S \) returns the integrated model \( \bar{M} \) to the local computers \( C_i \) for the next round of training. Since FL does not require data to be uploaded to the server during training, it can effectively avoid data leakage that may occur during data upload. Consequently, this approach is widely adopted in the financial industry. This paper reviewed and summarized the FL algorithms used in the financial industry in recent years, besides, sample dataset will be introduced, moreover, challenges faced by current FL algorithms will be identified.

2. Core Methodologies

In this section, we provide an overview of federated learning algorithms related to financial applications. We will start with the most basic algorithm and gradually introduce some variants of the algorithm. In addition, in order to have a clearer layout, this section will focus on several different aspects from the perspective of improving performance.

2.1. Aggregation Algorithm

The algorithm is designed mainly based on the training process of federated learning to improve model quality, accelerate model convergence, and ultimately reduce the amount of communication data. [10]

The core idea of the aggregation algorithm is to merge the local model updates of multiple clients to generate a global model. The following formula 1 well illustrates this idea. It indicates that the global objective function of federated learning is the weighted average of the local loss functions of each client, where the contribution of each client is proportional to the amount of data it has.

\( min\sum_{i = 1}^{N} \frac{n_{i}}{n}ℓ_{i}(x_{i},y_{i};ω) (1) \)

Where the ω is the parameter of the model, N represents the number of the clients, n_i represents the sample numbers of C_i, n is the total number of samples, l_i (x_i,y_i ;ω) is the loss function of the local client C_i. [8] After introducing the core idea of the aggregation algorithm, there are two classic federated learning aggregation algorithms that deserve further discussion: FedAvg (Federated Averaging) and FedSGD (Federated Stochastic Gradient Descent).

2.1.1. Federated Stochastic (FedSGD)

Inspired by stochastic gradient descent (SGD), FedSGD is an extension of SGD and is suitable in federated learning. By assuming there are multiple edge devices, each of the device calculates the gradient or parameters in the local data and send them to the central server for averaging and use the updated parameters for global model. [9]

2.1.2. Federated Averaging (FedAvg)

The FedAvg (Federated Averaging) algorithm is a variant based on stochastic gradient descent (SGD). The basic idea is that each client independently performs multiple iterations of model training on local data (performs multiple gradient updates), and then sends the updated model parameters to the central server. After the server receives the model parameters of all clients, it updates the global model by weighted averaging these parameters. [10] The equations below Shows the process of updating the model on the client and central server respectively.

\( w_k\gets\ w_k−\ \eta\nabla F_k(w_{k}) (2) \)

\( w_{t+1}\gets\ \sum_{k=1}^{k}\frac{n_k}{n}w_{k\ \ }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \)

Equation 2 calculates the local gradient and updates the local model \( w_k \) , among the parameters, \( \mathrm{\nabla}F_k(w_{k}) \) represents the loss function of the client k. Equation 3 shows the server aggregates updates from all clients to update the global model, among the parameters, \( n_k \) represents the number of client k, and n represents the total number of client data.

These two algorithms appear quite similar as both utilize SGD (Stochastic Gradient Descent) for training and send parameters to a central server. However, FedSGD is simpler in comparison because, unlike FedAvg, it sends updates to the server after every small computation rather than after multiple iterations of local training. One of the key characteristics of FedSGD is its intensive communication requirement, as clients must frequently send updates to the server after each computation. Due to this frequent communication, FedSGD may be less efficient than FedAvg in certain situations. [9]

2.1.3. Federated Proximal Optimization (FedProx)

FedAvg may experience slow or unstable convergence when processing highly heterogeneous data, because the model update directions of different clients may be quite different, causing interference in the optimization process of the global model. Hence, federated proximal optimization (FedProx) is proposed based on FedAvg. FedProx is a distributed proximal algorithm. Its core is to introduce a proximal term in each local gradient descent process to control the deviation between local updates and the global model. Specifically, FedProx limits the difference between the local model and the global model by adding a regularization term to the local loss function, thereby reducing the negative impact of data heterogeneity on model convergence. The proximal term is shown as below. [11]

\( f_{i,t}\ =\ arg{argmin}_{f\epsilon H}\left\{\ell_i\left(f\right)+\ \frac{1}{2\eta}\left|\left|f−f_{t−1}\right|\right|_H^2\right\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \)

Where \( \ell_i\left(f\right) \) represents the local loss function of the client. \( \eta \) is the step size or learning rate parameter. \( f_{t−1}\ \) are the global model parameters after the last round of communication.

2.2. Further protection using FL framework

Even though the FL algorithms above have provided a significant protection for model training in federated environment. But they do not by themselves fully address all the privacy issues inherent in federated learning. In order to further enhance data privacy and security, technologies such as Differential Privacy (DP) and Secure Multi-Party Computation (SMPC) can be introduced in the federated learning framework. [12]

2.2.1. Differential Privacy (DP)

DP introduces noise (normally Gaussian noise and Laplacian noise) to data such as model parameters to ensure that the results do not change significantly when a certain data point is added or removed. In other words, DP ensures that regardless of whether an individual's data is included, the results are almost the same to an attacker, thus protecting the privacy of individual data. [12] By adding artificial noise in model updates, DP can effectively prevent information leakage. Meanwhile, according to the way noise is introduced in the federated learning framework and the level of privacy protection, DP is divided into three different kinds, namely Centralized Differential Privacy (CDP), Local Differential Privacy (LDP), Distributed Differential Privacy (DDP). [13] The differences are listed in the table below.

Table 1. Comparison between different DPs

DP Method	Noise Addition Location	Trust Assumption	Privacy Protection Scope	Advantages	Disadvantages
Centralized Differential Privacy (CDP)	Central Server	Requires trusting the central server	Model updates from all clients	Easy to implement, high model accuracy	Relies on server trustworthiness, potential privacy leakage
Local Differential Privacy (LDP)	Locally at each client	Does not require trust in the server	Local data of each client	Comprehensive privacy protection, no need to trust the central server	High noise, may reduce model accuracy
Distributed Differential Privacy (DDP)	During distributed computation, often with MPC	Partially trusts the central server	Model updates and aggregation process	Balances privacy protection and model performance	Higher computational and communication complexity

2.2.2. Secure Multi-Party Computation (SMPC)

SMPC has been researched for over 40 years, the basic concept is to have multiple parties compute a function together, but each party does not expose its own input data. Under the FL framework, SMPC applications can be divided into two categories: server-based and client-based.

Server-side SMPC: All clients send processed data fragments to multiple independent servers, assuming that these servers are independent and not all corrupted.

Client SMPC: Usually there is only one server, and most of the security calculations are done by the client. [14]

By using SMPC in the FL framework, which significantly improves the security of the data, hence has been used widely in many industries, such as finance.

3. Applications

In the big data environment, users' private information and various data may be recorded by edge servers or smartphones. In this case, providing privacy protection is crucial for intelligent development. [15] This is where FL comes into play. With the help of many scholars, FL has become very important in many different fields, especially in finance. FL largely eliminates the possibility of fraud, theft and data breaches. [16] In this section, we will discuss some finance-related topics to fully demonstrate the application of FL in finance and explain some corresponding algorithms to provide a better understanding. Among them, financial fraud detection, as a main application, will be elaborated in detail, and some other applications will also be listed.

3.1. Financial Fraud Detection

Financial fraud is a serious problem that can cause huge losses to banks and consumers and has increased dramatically in recent years. As a result, financial fraud detection has become a hot topic, however, there are many shortcomings when using traditional method for financial fraud detection. For example, the shared data is quite limited due to cardholder privacy issues, moreover, traditional federated learning usually trains on their own private dataset. [17] In order to handle these issues, federated learning is introduced, it trains the dataset distributed on participating devices under certain coordination of a central sever. [18]

Among FL, several works have made impressive contribution. In the work done by Yang et, al, they proposed a fraud detection method based on federated learning framework. [17] The demonstration diagram is displayed below in Figure 2.

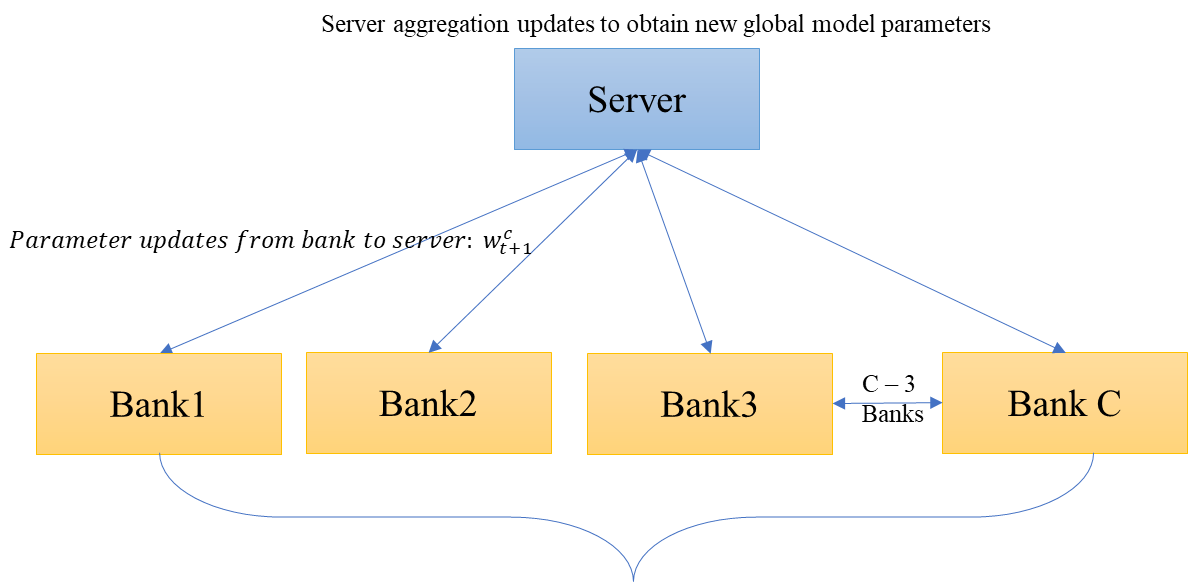
Figure 2. Basic flowchart of data transferring between central server and local banks

In the graph, \( w_{t+1}^c \) represents the updated parameters of the local bank, and it follows the equation below:

\( w_t→w_{t+1}^{c}=w_{t}−η∇Lc(x_{c},y_{c};w_{t}) \) (4)

Where \( w_t \) represents the current parameters, \( \eta \) represents the learning rate, \( \mathrm{\nabla Lc}(x_{c},y_{c};w_{t}) \) represents the loss gradient calculated by bank c based on its private dataset at time step t. Each bank downloads the shared model and trains it on local data. Then the model updates on each bank are sent to the central server, which aggregates the updates to improve the shared model, and the above process is repeated until the model converges. The formula for aggregated updates is shown in equation 4.

\( w_{t+1}=w_{t}−\sum_{c=1}^{C} \frac{n_{c}}{n}a_{t+1}^{c}w_{t+1}^{c} \) (5)

Where \( a_{t+1}^c \) is the model performance metrics for bank c, it indicates the influence for the whole model, making it play a more important role in the global model update. \( w_{t+1}^c \) represents the local model parameters update.

This approach allows different banks to jointly train fraud detection models without sharing their private data, which greatly helps protect user privacy. Not only that, the author used the deep learning model CNN for training and achieved good results. Using a dataset of European credit card (ECC) transactions made by European cardholders in September 2013 provided by ULB ML Group, which contains 284,807 transactions, only 0.172% (492 cases) of transactions were fraudulent. Therefore, using SMOTE to rebalance the dataset, the results are greatly improved compared to traditional methods, with AUC=95% and F1 score=82%.

Not only this, in the work done by Lv et, al, on the premise of meeting privacy protection requirements, they proposed an idea of using vertical federated learning technology to combine financial and social features to build a federated learning model for social financial fraud accounts. [19] Different from the first sample, this work incorporates social characteristics. Not only that, but the application scenarios are also different. This work is more applied to two different companies, and calculations and model parameter updates are completed through encryption model training., the data is always kept locally, and only encrypted intermediate results are calculated. Figure 3 below shows the working process of the framework.

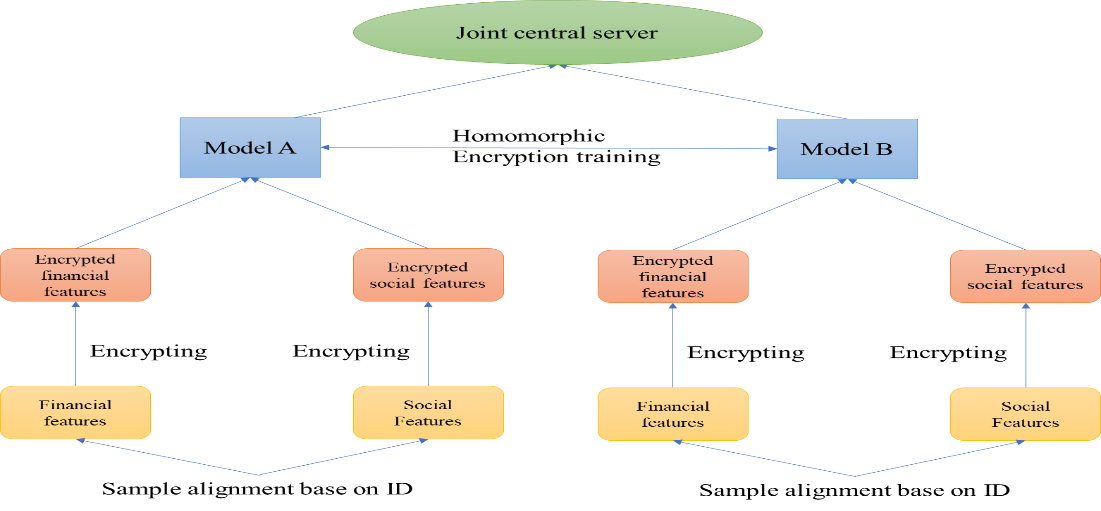
Figure 3. Working process of the framework.

From the given diagram, it is clear that the process follows a certain step, First, the features of financial and social data are extracted respectively, and the data is encrypted during the alignment and transmission process. Then, each bank performs model training locally, calculates the gradient update, and sends the encrypted gradient update to the central server after training. Finally, the central server aggregates the updates from each bank, updates the global model parameters, and distributes them back to each bank.

Then, based on this framework, the author uses two different algorithms to train separately under different conditions to compare the results. In the experiment, logistic regression (LR) which is designed for linear model, and Gradient Boosting Decision Tree (XGBoost), which is suitable for complex non-linear relationships are used here, meanwhile, author utilized two situations, with financial features and with both financial and social features respectively and had gotten the result listed in the table 2.

Table 2. The result gotten of two models and two situations

features model LR XGBoost

Only financial features

Accuracy: 0.693

AUC: 0.8

Accuracy: 0.947

AUC: 0.95

Financial and social features

Accuracy: 0.752

AUC: 0.845

Accuracy: 0.959

AUC: 0.96

From the result, it is clear that the performance of the models is improved when using federated learning framework with both financial and social features.

In addition, there are other works that have made great contributions. They are listed in the table 2 below in chronological order. For each work, the year, the name of the author, the data set, method used, and the results obtained will be listed one by one in the table 3.

Table 3. Other related works

Year	Author	Method	Dataset	Result
2019 [17]	W. Yang et.al	FL + CNN	ULB ML (ECC transaction)	AUC = 95% F1 = 82%
2020 [21]	W. Zheng et.al	FL + like metric learning + Deep K-tuplet network + ResNet-34	Four datasets: ECC, RA, SD, Vesta	Best accuracy: 99.98% on ECC dataset
2021 [19]	B. Lv et.al	FL + LR / FL + XGBoost	Customized Dataset	FL + LR: Accuracy: 0.752 ACU: 0.845 FL + XGBoost: Accuracy: 0.959 AUC: 0.96
2024 [20]	M. Abdul Salam et.al	FL + Hybrid Methods) - Classifiers (RF, LR, KNN, DT, GaussianNB)	ULB ML (ECC transaction)	Best accuracy: Random Forest (RF): 99.99%
2024 [22]	T. Baabdullah et.al	FL + Blockchain + machine learning algorithms	ULB ML (ECC transaction)	Best accuracy: 99.99% with Random Forest (RF)
2024 [23]	Md. S. I. Khan et.al	SWIFT Dataset AMLSim dataset	FL + Relational Data (Fed-RD) / Differential Privacy (DP) / Secure Multiparty Computation (MPC)	Achieved maximum AUPRC of 80% on the SWIFT dataset and 90% on the AMLSim dataset

3.2. Other Applications

3.2.1. Supply Chain Financing Prediction

When assessing an enterprise's credit and supply chain financing risks, the company may be reluctant to share detailed order-level information with the funder. [24] applies the FL framework based on 1D-CNN to assess supply chain financing risks while minimizing the exposure of sensitive order information, thereby enabling order-level risk assessment.

Due to regulatory restrictions, lenders' credit data cannot be centrally modeled. [25] proposed an explainable vertical federated learning (EVFL) framework incorporating a counterfactual explanation module. This framework helps banks address lender assessment challenges without centralizing credit data. The explainable model allows bank staff to intuitively understand customers' credit levels.

3.2.2. Financial Audit

As companies enhance their financial supervision, large audit firms must audit clients' multi-dimensional information while ensuring that auditors maintain confidentiality and accountability. [26] employed the FL framework to train deep learning models, enabling auditors to review the multi-dimensional accounting information of multiple clients while safeguarding data security. The framework incorporates differential privacy and segmentation learning to mitigate the risk of data leakage.

3.2.3. Malicious Transactions in Digital Currency

The anonymity of digital currency offers a natural shield for financial criminals, leading to the rise of various malicious digital currency transactions. Centralized learning methods heighten the risk of user transaction data leakage. [27] employs the federated learning framework to train a graph neural network model, constructing graphs of transaction data from different sub-nodes and submitting the gradient data of the local graphs to a server for aggregation, enabling the identification of malicious transactions in the digital currency market. This approach safeguards user transaction data privacy while effectively detecting malicious transactions and preserving the integrity of the virtual financial market.

4. Dataset

This section discusses several datasets for training federated learning in the financial domain.

4.1. Elliptic Dataset

The Elliptic dataset [28] comprises over 200,000 Bitcoin transactions, represented as a graph network. In this network, nodes signify individual Bitcoin transactions, while edges illustrate the flow of Bitcoin between users. The dataset categorizes transactions into legal transactions (such as exchanges, legal services, etc.) and illegal transactions (such as scams, malicious activities, Ponzi schemes, etc.).

4.2. Lending Club Dataset

The Lending Club dataset [29] includes loan issuance information from 2007 to 2018. It contains financial details such as users' credit scores and the number of financial inquiries, which are used to predict loan statuses (e.g., 'overdue,' 'paid in full').

4.3. Kaggle Credit Card Fraud (2013) Dataset

The Kaggle Credit Card Fraud (2013) dataset [30] contains transactions made by European cardholders over two days in September 2013. It includes a categorical variable indicating whether a transaction was deemed fraudulent (True) or not (False). The dataset comprises a total of 284,807 transaction records, with only 492 marked as fraudulent.

5. Challenges and Future Works

5.1. Challenges

The FL algorithm allows data to remain on local devices for training, with the trained sub-models uploaded to the cloud for aggregation. This approach effectively mitigates the risk of data leakage associated with data uploads. However, uploading models introduces security vulnerabilities. During the process of uploading the model to the server, malicious actors may exploit opportunities to attack the model's parameters, potentially degrading its performance or even stealing sensitive data [31],[32]. Model attacks can have significant negative impacts. For instance, attackers might distort the model's judgment, preventing it from identifying malicious digital currency transactions or accurately auditing the financial status of relevant individuals, thereby aiding financial criminals in evading legal sanctions. As discussed in the chapter 2.2.1, differential privacy [33] is a method used in FL to protect models by adding perturbations to sub-models before uploading them. However, a 2023 study [34] found that attackers can exploit noise to evade anomaly detection, making it difficult to identify perturbations that have been maliciously injected into the model. Therefore, how to protect the model during the uploading process is still one of the issues that deserves attention.

Since the FL algorithm allows different users to train sub-models on local computers, varying architectures among these sub-models can hinder effective aggregation, leading to model heterogeneity [35]. Similar challenges include statistical heterogeneity [36]. Even within the same subfield, user data from different financial companies may vary significantly. For example, one audit firm may possess records of a client’s expenses and income, while another may also hold documentation of the client’s real estate holdings. These discrepancies result in data across companies not following the same distribution, leading to inconsistent convergence when updating sub-models. Additionally, when different financial institutions use varying devices to train sub-models, device heterogeneity arises [37], leading to models being effectively updated on devices with strong computing power, while devices with weaker capabilities may struggle to do so. This disparity can result in some financial institutions' models not being updated in a timely manner, exposing them to attacks from financial criminals who exploit outdated models or engage in data theft and other illegal activities.

5.2. Future Works

Future work will focus on developing model protection algorithms to safeguard sub-models from attacks during the upload process. The simplest approach to addressing the heterogeneity problem is for the server provider to specify the data format, model architecture, and device requirements. Additionally, the use of knowledge distillation techniques can be explored to address the challenge of fusing models with different architectures.

For example, the server model is regarded as the teacher model, while the sub-models trained by each user are considered student models. Users can utilize a public dataset to obtain output from the teacher model and adjust their sub-models, accordingly, aligning their outputs with that of the teacher model. Finally, the user's private dataset is used to fine-tune the sub-model.

6. Conclusion

In this paper, we provided a comprehensive overview of federated learning algorithms and their applications within the financial sector. We began by reviewing existing literature, covering a range of federated algorithms from basic aggregation methods to more advanced frameworks incorporating Differential Privacy (DP) and Secure Multi-Party Computation (MPC). A comparative analysis of these algorithms was conducted, with the results presented in tabular form. We then explored the application of federated learning in the financial domain, particularly focusing on financial fraud detection. We reviewed existing works in this industry, conducted a thorough comparison, and highlighted other relevant financial applications. Then, the sample dataset is introduced. Finally, we discussed the challenges associated with applying federated learning in financial contexts. These challenges provide valuable insights for future research directions and underscore the potential for further advancements in federated learning within the financial sector.

Acknowledgments

Kang Ruixin, Li Qihui and Lu Haodong contributes equally and should be considered co-first authors

References

[1]. P. Weber, K. V. Carl, and O. Hinz, “Applications of Explainable Artificial Intelligence in Finance—a systematic review of Finance, Information Systems, and Computer Science literature,” Management Review Quarterly, Feb. 2023, doi: 10.1007/s11301-023-00320-0.

[2]. L. Cao, “AI in Finance: Challenges, Techniques, and Opportunities,” ACM Computing Surveys, vol. 55, no. 3, pp. 1–38, Feb. 2022, doi: 10.1145/3502289.

[3]. M. Alazab, S. P. Rm, P. M, P. K. R. Maddikunta, T. R. Gadekallu, and Q.-V. Pham, “Federated Learning for Cybersecurity: Concepts, Challenges, and Future Directions,” IEEE Transactions on Industrial Informatics, vol. 18, no. 5, pp. 3501–3509, May 2022, doi: 10.1109/tii.2021.3119038.

[4]. C. Zhang, Y. Xie, H. Bai, B. Yu, W. Li, and Y. Gao, “A survey on federated learning,” Knowledge-Based Systems, vol. 216, p. 106775, Mar. 2021, doi: 10.1016/j.knosys.2021.106775.

[5]. S. Sun, C. Si, G. Wu, and S. Gong, “Federated zero-shot learning with mid-level semantic knowledge transfer,” Pattern Recognition, p. 110824, Jul. 2024, doi: 10.1016/j.patcog.2024.110824.

[6]. J. P. Albrecht, “How the GDPR Will Change the World,” European Data Protection Law Review, vol. 2, no. 3, pp. 287–289, Jan. 2016, doi: 10.21552/edpl/2016/3/4.

[7]. F. Yang, Y. Qiao, M. Z. Abedin, and C. Huang, “Privacy-Preserved Credit Data Sharing Integrating Blockchain and Federated Learning for Industrial 4.0,” IEEE Transactions on Industrial Informatics, vol. 18, no. 12, pp. 8755–8764, Dec. 2022, doi: 10.1109/tii.2022.3151917.

[8]. A. Grataloup, S. Jonas, and A. Meyer, “A review of federated learning in renewable energy applications: Potential, challenges, and future directions,” Energy and AI, vol. 17, p. 100375, Sep. 2024, doi: 10.1016/j.egyai.2024.100375.

[9]. Z. Li, V. Sharma, and S. P. Mohanty, “Preserving Data Privacy via Federated Learning: Challenges and Solutions,” IEEE Consumer Electronics Magazine, vol. 9, no. 3, pp. 8–16, May 2020, doi: 10.1109/mce.2019.2959108.

[10]. H. B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. y Arcas, “Communication-Efficient Learning of Deep Networks from Decentralized Data,” arXiv.org, Feb. 17, 2016. https://arxiv.org/abs/1602.05629

[11]. L. Su, J. Xu, and P. Yang, “A Non-parametric View of FedAvg and FedProx: Beyond Stationary Points,” arXiv.org, Jun. 29, 2021. https://arxiv.org/abs/2106.15216

[12]. D. Byrd and A. Polychroniadou, “Differentially Private Secure Multi-Party Computation for Federated Learning in Financial Applications,” arXiv.org, Oct. 12, 2020. https://arxiv.org/abs/2010.05867

[13]. S. Yu and L. Cui, “Differential Privacy in Federated Learning,” in Digital Privacy and Security, Singapore: Springer Nature Singapore, 2022, pp. 77–88. Accessed: Aug. 10, 2024. [Online]. Available: http://dx.doi.org/10.1007/978-981-19-8692-5_5

[14]. S. Yu and L. Cui, “Secure Multi-party Computation in Federated Learning,” in Digital Privacy and Security, Singapore: Springer Nature Singapore, 2022, pp. 89–98. Accessed: Aug. 10, 2024. [Online]. Available: http://dx.doi.org/10.1007/978-981-19-8692-5_6

[15]. J. Wen, Z. Zhang, Y. Lan, Z. Cui, J. Cai, and W. Zhang, “A survey on federated learning: challenges and applications,” International Journal of Machine Learning and Cybernetics, vol. 14, no. 2, pp. 513–535, Nov. 2022, doi: 10.1007/s13042-022-01647-y.

[16]. M. Narula, J. Meena, and D. K. Vishwakarma, “A comprehensive review on Federated Learning for Data-Sensitive Application: Open issues & challenges,” Engineering Applications of Artificial Intelligence, vol. 133, p. 108128, Jul. 2024, doi: 10.1016/j.engappai.2024.108128.

[17]. W. Yang, Y. Zhang, K. Ye, L. Li, and C.-Z. Xu, “FFD: A Federated Learning Based Method for Credit Card Fraud Detection,” in Lecture Notes in Computer Science, Cham: Springer International Publishing, 2019, pp. 18–32. Accessed: Aug. 06, 2024. [Online]. Available: http://dx.doi.org/10.1007/978-3-030-23551-2_2

[18]. J. Konečný, H. B. McMahan, F. X. Yu, P. Richtárik, A. T. Suresh, and D. Bacon, “Federated Learning: Strategies for Improving Communication Efficiency,” arXiv.org, Oct. 18, 2016. https://arxiv.org/abs/1610.05492

[19]. B. Lv, P. Cheng, C. Zhang, H. Ye, X. Meng, and X. Wang, “Research on Modeling of E-banking Fraud Account Identification Based on Federated Learning,” in 2021 IEEE Intl Conf on Dependable, Autonomic and Secure Computing, Intl Conf on Pervasive Intelligence and Computing, Intl Conf on Cloud and Big Data Computing, Intl Conf on Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech), Oct. 2021. Accessed: Aug. 07, 2024. [Online]. Available: http://dx.doi.org/10.1109/dasc-picom-cbdcom-cyberscitech52372.2021.00105

[20]. M. Abdul Salam, K. M. Fouad, D. L. Elbably, and S. M. Elsayed, “Federated learning model for credit card fraud detection with data balancing techniques,” Neural Computing and Applications, vol. 36, no. 11, pp. 6231–6256, Jan. 2024, doi: 10.1007/s00521-023-09410-2.

[21]. W. Zheng, L. Yan, C. Gou, and F.-Y. Wang, “Federated Meta-Learning for Fraudulent Credit Card Detection,” in Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Jul. 2020. Accessed: Aug. 07, 2024. [Online]. Available: http://dx.doi.org/10.24963/ijcai.2020/642

[22]. T. Baabdullah, A. Alzahrani, D. B. Rawat, and C. Liu, “Efficiency of Federated Learning and Blockchain in Preserving Privacy and Enhancing the Performance of Credit Card Fraud Detection (CCFD) Systems,” Future Internet, vol. 16, no. 6, p. 196, Jun. 2024, doi: 10.3390/fi16060196.

[23]. Md. S. I. Khan, A. Gupta, O. Seneviratne, and S. Patterson, “Fed-RD: Privacy-Preserving Federated Learning for Financial Crime Detection,” arXiv.org, Aug. 03, 2024. https://arxiv.org/abs/2408.01609

[24]. L. Kong, G. Zheng, and A. Brintrup, “A federated machine learning approach for order-level risk prediction in Supply Chain Financing,” International Journal of Production Economics, vol. 268, p. 109095, Feb. 2024, doi: 10.1016/j.ijpe.2023.109095.

[25]. P. Chen, X. Du, Z. Lu, J. Wu, and P. C. K. Hung, “EVFL: An explainable vertical federated learning for data-oriented Artificial Intelligence systems,” Journal of Systems Architecture, vol. 126, p. 102474, May 2022, doi: 10.1016/j.sysarc.2022.102474.

[26]. M. Schreyer, T. Sattarov, and D. Borth, “Federated and Privacy-Preserving Learning of Accounting Data in Financial Statement Audits,” Oct. 2022, doi: 10.1145/3533271.3561674.

[27]. H. Du, M. Shen, R. Sun, J. Jia, L. Zhu, and Y. Zhai, “Malicious Transaction Identification in Digital Currency via Federated Graph Deep Learning,” IEEE INFOCOM 2022 - IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), May 2022, doi: 10.1109/infocomwkshps54753.2022.9797992.

[28]. A. Mohan, K. PV, P. Sankar, K. M. Manohar, and A. Peter, “Improving anti-money laundering in bitcoin using evolving graph convolutions and deep neural decision forest,” Data Technologies and Applications, vol. 57, no. 3, pp. 313–329, Nov. 2022, doi: 10.1108/dta-06-2021-0167.

[29]. S. Fu, C. Xie, B. Li, and Q. Chen, “Attack-Resistant Federated Learning with Residual-based Reweighting,” arXiv (Cornell University), Jan. 2019, doi: 10.48550/arxiv.1912.11464.

[30]. A. D. Pozzolo, O. Caelen, R. A. Johnson, and G. Bontempi, “Calibrating Probability with Undersampling for Unbalanced Classification,” Dec. 2015, doi: 10.1109/ssci.2015.33.

[31]. Y. Huang, S. Gupta, Z. Song, K. Li, and S. Arora, “Evaluating Gradient Inversion Attacks and Defenses in Federated Learning,” arXiv (Cornell University), Jan. 2021, doi: 10.48550/arxiv.2112.00059.

[32]. A. Yazdinejad, A. Dehghantanha, H. Karimipour, G. Srivastava, and R. M. Parizi, “A Robust Privacy-Preserving Federated Learning Model Against Model Poisoning Attacks,” IEEE Transactions on Information Forensics and Security, p. 1, Jan. 2024, doi: 10.1109/tifs.2024.3420126.

[33]. M. Abadi et al., “Deep Learning with Differential Privacy,” Oct. 2016, doi: 10.1145/2976749.2978318.

[34]. M. Yang, H. Cheng, F. Chen, X. Liu, M. Wang, and X. Li, “Model poisoning attack in differential privacy-based federated learning,” Information Sciences, vol. 630, pp. 158–172, Jun. 2023, doi: 10.1016/j.ins.2023.02.025.

[35]. G. Long, Y. Tan, J. Jiang, and C. Zhang, “Federated Learning for Open Banking,” in Lecture notes in computer science, 2020, pp. 240–254. doi: 10.1007/978-3-030-63076-8_17.

[36]. Y. Liu et al., “Vertical Federated Learning: Concepts, Advances, and Challenges,” IEEE Transactions on Knowledge and Data Engineering, pp. 1–20, Jan. 2024, doi: 10.1109/tkde.2024.3352628.

[37]. T. Li, A. K. Sahu, A. Talwalkar, and V. Smith, “Federated Learning: Challenges, Methods, and Future Directions,” IEEE Signal Processing Magazine, vol. 37, no. 3, pp. 50–60, May 2020, doi: 10.1109/msp.2020.2975749.

Cite this article

Kang,R.;Li,Q.;Lu,H. (2024). Federated machine learning in finance: A systematic review on technical architecture and financial applications. Applied and Computational Engineering,102,61-72.

Data availability

The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.

Disclaimer/Publisher's Note

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

About volume

Volume title: Proceedings of the 2nd International Conference on Machine Learning and Automation

ISBN：978-1-83558-693-8(Print) / 978-1-83558-694-5(Online)

Editor：Mustafa ISTANBULLU

Conference website: https://2024.confmla.org/

Conference date: 12 January 2025

Series: Applied and Computational Engineering

Volume number: Vol.102

ISSN：2755-2721(Print) / 2755-273X(Online)

© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license. Authors who publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See Open access policy for details).