1. Introduction

PID controllers are important in the field of robot and mechanical system control because of their strength in adaptability and simplicity. There are still research gaps in the theory and clever tuning strategies of PID controllers when dealing with nonlinear systems and uncertainties, despite the current control theory's rapid progress and the widespread use of classical PID methods. The objective of this research is to investigate this gap, look at the PID controller's theoretical design, and look at how intelligent tuning technology is used in mechanical systems. This research aims to analyze PID parameter optimization techniques and investigate the shortcomings of current tuning procedures through a review of relevant literature and case examples. The importance of this research lies in its capacity to bridge the gap between conventional control strategies and contemporary tuning methods, offering both theoretical and practical assistance for enhancing system performance and stability in unpredictable and complex situations.

2. The theory and architecture of PID controller

2.1. The structure of PID controller

A PID controller is called a PID controller because its output is the sum of three variables: the proportional, integral, and derivative terms, expressed as \( K_P \) , \( K_I \) and \( K_D \) . These parameters \( K_P \) , \( K_I \) and \( K_D\ \) are related to the error item e between the input and output parameters.where \( K_P \) , \( K_I \) and. \( K_I \) and \( K_D \) stand for the relevant P, I, and D parameters.

can be represented by Equation(1).

\( K_I=K_P\times T_i \) , \( K_D=K_P\times\frac{1}{T_d} \) (1)

where \( T_i \) and \( T_d \) stand for the respective derivative and reset times.

A system's response type is determined by its reset and derivative timings. The properties of the controller variables P, I, and D are introduced and explained in brief as follows:

Proportional term(P)The closed-loop time constant reduces as the proportional parameter does, which aids the reaction. However, because the output is precisely proportionate to the input, it guarantees that the system order remains unchanged. Nevertheless, the steady-state error or offset persists even after the proportional parameter is decreased. The proportional element's primary responsibility is to proportionally check the error's size and the PID controller's reaction.P is represented by Equation (2) in the proportional term as

\( P_{out}=K_{p^e} \) (2)

Where

\( P_{out} \) : percentage of the controller's output,

\( K_p \) : proportionate profit,

\( e \) : error phrase

Integral term (I):The offset is removed when this parameter increases the nature and order of the system by one. This option causes the system to oscillate continuously while simultaneously speeding up the system's reaction time. Integral control aims to address the proportional control problem, which analyzes how errors evolve with time and gradually raises a minor error. The integral control adjustment is represented by a temporal factor called reset rate.

\( L_{out}=\frac{1}{T_i}\int\ e \) \( dt=K_I \) \( \int\ e \) \( dt \) (3)

Where

\( L_{out} \) :is a crucial component of the controller's output.

\( T_i \) :integral time, reset time,

\( K_i \) :integral gain, \( e \) : erroe phrase

Term of derivative (D): In essence,the oscillatory response of the system is reduced by this setting. It is unrelated to the offset, nature, or order of the system. It looks at the rate of change of the error signal.

Derivatives lead to larger systematic responses to fast change. Over time, derivative phrases change. Overshooting or control instability may result from using too many derivative terms.The symbol for it is Equation (4).

\( D_{out}=T_d\frac{d}{dt}e=K_D\frac{d}{dt}e \) (4)

\( D_{out} \) :is the controller's output derivative,

\( T_d \) :derivative time,

\( K_d \) :derivative gain, \( \ e \) :error phrase

A PID control system's typical configuration is shown in Fig. 1. The error term \( \ e(t) \) between the set value and the actual output is recalculated when the set value \( r(t) \) changes.The \( K_P \) , \( K_I \) , and \( K_D \) parameter actions are constructed using the \( e(t) \) error signal or term, and the weighted and summed signals are then applied to the plant model as the \( u(t) \) control signal.This results in the output signal \( y(t) \) . This corrected, real signal will be sent to the controller, which will then recalculate the incorrect signal. The newly received control signal \( u(t) \) is received by the plant. This procedure will continue until a steady-state error is encountered.

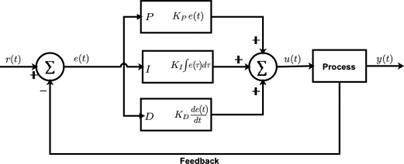
Figure 1. Fundamental PID control structure.

3. PID controller tuning methods

3.1. Classical tuning methods

Classical methods of tuning PID controllers found in the literature include the trial and error method, the Ziegler-Nichols step response method (Taylor Instrument Company, USA, 1941 and 1942), the Ziegler-The Cohen-Kuhn method (1953), the relay tuning method, and the Nicholz frequency response method [1]. Furthermore, for processes with a dead-time constant ratio between 0.1 and 1, Weng Kun-ho et al. examine the robustness and efficiency of the well-known PID formulas (Ziegler-Nichols, Cohen-Kuhn, and tuning formulas) [2].It has been noted that Ziegler-Nichols achieves a gain margin of around 1.5. The tuning formula is adjusted to determine the load perturbation integral's integral absolute error (IAE), integral square error (ISE), and integral time absolute error. The phase margin rises from around 30 to 60 as the process's dead-time to time constant ratio goes from 0.1 to 1. The phase margin is around 65 and the proper gain margin is 2.Observe how to maximize the set point response by utilizing the adjustment formula.

In order to eliminate process poles, these formulas mainly utilize the zero point of the PID controller. The traditional tuning method looks for a graphical or analytical feature in the process that may be used to determine the controller setting, based on a number of assumptions about the factory and the intended output. These techniques are incredibly quick to calculate and easy to put into practice. These approaches work well initially, but because of the assumptions made, they may not always produce the intended results. As a result, more modifications are required

3.2. Intelligent tuning methods

After the advent of classical PID controller tuning techniques, complex system and controller designer performance requirements require the introduction of new tuning design techniques. We have made several helpful advancements in PID tuning techniques over the years, enabling us to handle more complicated systems and more precise performance requirements. Only the FOPDT (first order plus dead time) and SOPDT (second order plus dead time) models could be tuned using the earlier classical techniques. One drawback of the conventional PID control tuning approach is it.In 1988, Fong-Chwee et al. created self-tuning PID controllers using pole assignment technology. Three kinds of self-tuning PID controllers that can provide better control over certain dead zone process aspects are discussed. Some researchers were creating adjusting techniques in 1992,such as self-adjustment [3], genetic algorithm methods [4] Pattern matching method [5].Alberto Leva, in 1993, suggested an automatic relay-based PID tuning technique to get regulator tuning by describing the process frequency response at a point and assuming a process model structure.[6]The algorithm can commonly offer accurate and performance results that are sufficient if the imagined process structure is near to reality. (1993) Chuang and Atherton assessed the process required to attain the best configuration for their PID controller. A formula for configuring the parameters of the FOPDT (first order plus dead time) factory controller, which is widely used in the process industry, is subsequently obtained using this method.[7]. In 1999, Wang Qinguo [8] introduced a new PID tuning method, which performs well across a number of linear self-tuning techniques.The basis is to adjust the process's frequency response to a specific SOPDT structure, which can mimic the oscillatory and monotonic characteristics of the process.

4. PID applications in the field of mechanics

PID control technology is essential to the automation and precision engineering domains. In-depth discussion of PID controller applications in robotic manipulators and other mechanical systems, along with an analysis of their benefits and drawbacks in various control scenarios, will be covered in this article. The evolution and innovation of PID control technology will be demonstrated by the important research projects that this article reviews, ranging from conventional PD or PID algorithms to more sophisticated intelligent control techniques.

4.1. PID for robotic manipulator

Despite advancements in modern control theory, conventional PD or PID algorithms are still often used by robotic manipulator controllers, mostly because to their conceptual simplicity and straightforward tuning processes. A distributed pole assignment feedback-based robot control approach was proposed by Y. Bestaoui [9]. In addition, Zhang Hong [10] performs the optimal PID digital implementation of the robot operator. Later, the stability of PID control of an industrial robot arm was demonstrated by Paul Rocco and Dong Sun et al. Robots and other comparable dynamic devices with nonlinear models are now able to use PID control.

There are three primary areas of study for PID controllers used in robot applications. The first section deals with the use of intelligent controls for PID gain modification, such as fuzzy control, neural networks, or genetic techniques. The second field of study focuses on PID gain selection strategies that employ control strategies like inverse dynamic control or optimal control. PID gain selection techniques that directly and similarly use Lyapunov stability analysis constitute a third category of study areas, in [11] addressing global asymptotic control of robotic manipulations under input limitations, with and without velocity measurements.

For nonlinear second-order objects, Chang et al. presented the gain selection method of robust PID control [12]. PID gain for erroneous models can also be easily and effectively adjusted using the method in [12]. Furthermore, it offers a comparable relationship in the discrete time domain between PID control and TDC (time delay control). According to a recent study [13]. A new nonlinear self-tuning PID controller (NSPIDC) was presented by Pradhan and Subudhi to regulate the joint position and linkage deflection of a flexible link robotic arm (FLM) under varying payload conditions.Robotic hands were the subject of an application of a novel discrete-time PID control technique dubbed PID + by Shaban et al.[14].

4.2. PID for mechanical systems

PID control technique is used in most industrial mechanical systems. PID control method is explored for the following applications: traction crane, grab, continuous tension control system, magnetic deviation system, milling process, four-wheel turbine, double-rotor MIMO system, and so on.

In [15] Matinen et al., for cascade PID controllers used in crane applications, a straightforward root technique is offered. Homberg et al. a PID control method is suggested for laser surface hardening of steel. A class of mechanical systems (such inertia wheels, cranes, ball oscillations, etc.) that may be globally stabilized with linear PID was identified by Jose Romero et al.[16]. The algorithm and associated findings from Chun-Shen Wei and Dirksovke's design of a magnetic bearing controller, which includes optimization through multi-objective genetic algorithms, are presented [17]. In a similar vein, [18] suggests a novel active control method to lessen flutter noise during milling.

Otis et al. In [19], A nonlinear robust controller design and implementation technique for attitude correction in an experimental pilot's aerial vehicle (UAV) framework is provided. A PID-based control approach for a maglev system is provided. To control paw rotation, a fuzzy PID controller tuning approach based on saturation is provided. A recent research proposes an optimal fractional fuzzy PID control for constant tension control systems.

5. Conclusion

The PID controller, due to its simple structure and easy implementation, has been widely used in the field of industrial control. With the advancement of technology, PID control theory is also continuously progressing, with many improved and optimized methods emerging. For example, the fractional-order PID controller introduces the concept of fractional calculus, providing more flexibility and precision, especially suitable for systems with nonlinearity, time-varying characteristics, or long time delays. Intelligent PID control combines artificial intelligence technology, giving the control system more intelligent performance and features, and has been widely used in the fields of industrial control and robotics. In the future, PID control will continue to develop towards more intelligent, adaptive, and optimized directions. Intelligent PID control will combine advanced intelligent algorithms and technologies to adapt to more complex and variable industrial environments. At the same time, research and application of PID controllers will continue to expand into fields such as numerical control systems, providing more accurate and efficient control solutions. The automatic tuning function of PID controllers will also continue to be of interest to industrial users, becoming a major area of research