1. Introduction

The Multi-Armed Bandit (MAB) algorithms is an effective solution to sequential decision-making under uncertainty. When decision-makers fall into an Exploration-Exploitation (EE) dilemma, MAB algorithms balance exploration and exploitation, updating the expected reward of each option in the process of constantly trying different options, thereby helping agents make better choices in uncertain environments. MAB algorithms have gradually become a powerful tool for solving online decision-making problems due to its advantages such as effective balance between exploration and utilization, strong adaptability, and solid theoretical foundation.

MAB application scenarios often involve real-time decision-making and dynamic environments, which makes the algorithm extremely practical in modern technology and business. Upper Confidence Bound (UCB) Algorithm and Thompson Sampling (TS) Algorithm are typical and efficient MAB algorithms.

Previously, some studies have compared the performance of some classic MAB algorithms. For example, Hu conducted a comprehensive comparison and analysis of the performance of three algorithms (UCB, ETC, and TS) in different environments by analyzing the algorithm principles and experimental simulations. The characteristics and some limitations of these algorithms were pointed out, emphasizing the stability of the UCB algorithm through the strategy of selecting actions by selecting the maximum confidence upper bound, as well as its ability to quickly adapt to the environment; and the flexibility of the TS algorithm due to its randomization [1]. Kong et al. analyzed the practical application of the MAB algorithm in the problem of two-sided matching markets, solved some challenges faced by the TS algorithm in this problem, compared the differences between the TS algorithm and the UCB algorithm in this problem, and through a large number of experiments, concluded that the TS algorithm has unique advantages over the Explore-Then-Commit (ETC) algorithm and the UCB algorithm [2].

In addition, Banaeizadeh et al. proposed a solution to the problem of severe interference of the uplink of high-altitude Unmanned Aerial Vehicle (UAV) line-of-sight channels to ground users. The results of the simulation experiment show that by simulating ε-Greedy algorithm, UCB algorithm and TS algorithm, the optimal action pair is selected to alleviate the problem of UAV uplink interference, which can effectively reduce the interference of UAVs to their ground users on the same channel. At the same time, the performance of these three algorithms in dealing with this problem is also evaluated in the simulation results, emphasizing that the UCB algorithm and the TS algorithm have higher accuracy in selecting the best action [3]. Shi et al. analyzed and compared ε-Greedy, UCB with TS, demonstrated several applications of TS in multiple fields and their modeling process, and emphasized the advantages of TS algorithm in solving MAB problems [4]. In their research, Umami and Rahmawati used TS, ε-Greedy and UCB-1 to optimize A/B testing in the context of advertising marketing, and compared the three algorithms, proposing that the behavior of ε-Greedy is very unstable. TS can improve long-term results overall, but produces more noise, while UCB-1 is more reliable due to its better accuracy and noise tolerance [5].

There are many papers pointing out the advantages and wide applications of the TS algorithm. For example, Kalkanli and Ozgur's study on the asymptotic convergence of the TS algorithm emphasized the accuracy and consistency of the TS algorithm in finding the optimal action [6]. Zhong et al. re-studied cascading bandits and pointed out that based on the experience of previous studies on cascading bandits, the TS algorithm has more advantages than the UCB algorithm. Then, a more stringent regret upper bound was proposed for the TS algorithm with Beta-Bernoulli prior than the conclusions of previous researchers. The TS algorithm with Gaussian updates was also proposed and analyzed, and the performance of the TS algorithm proposed in the paper was proved to be better than the existing UCB-based algorithms [7]. Chaouki et al. designed a new search algorithm, Thompson Sampling Decision Trees (TSDT), based on the classic prediction model decision tree in machine learning and combined with the TS algorithm. They proved the excellent performance of the algorithm in generating the best tree through a large number of experiments. The test results from many aspects show that TSDT is superior to the existing algorithms [8]. Wang's research mentioned three application scenarios of the TS algorithm, namely advertising delivery, multi-target search and tracking, and Fog Computing. It pointed out that the TS algorithm has a very broad application prospect. At the same time, it also pointed out that the algorithm has low efficiency under certain conditions and urgently needs to improve its universality [9]. Zhu and Tan's research focused on the risk problem in online decision-making, explored the Mean-Variance Bandits that measure risk with mean variance, and introduced the TS algorithm for it, achieving the best regret bound of Mean-Variance MABs and performing well in risk tolerance [10].

Sometimes researchers combine TS with other exploration-exploitation policies, such as ε-Greedy, to improve the performance of the algorithm. Jin et al. proposed ε-Exploring Thompson Sampling (ε-TS) in their research. Through theoretical analysis and experimental results, they proved that ε-TS is more computationally efficient than TS and achieves a better regret bound [11]. Do et al. studied TS in Bayesian optimization and improved TS by combining ε-Greedy. They proved that the improved algorithm has excellent performance through empirical evidence [12]. Current studies comparing and analyzing several MAB algorithms focus on classic multi-armed bandit algorithms, such as UCB, ETC, and TS algorithm. There are few studies on hybrid algorithms such as the ε-TS, and no studies have compared and analyzed the performance of hybrid strategies with TS and the classic MAB algorithm in the context of multi-armed bandits. This study is based on the environment of custom-designed simulated Multi-Armed Bandits where rewards follow bernoulli distribution, and the data analyzed in this study are generated from the custom-designed simulated Multi-Armed Bandits.This paper compares and analyzes the performance of UCB, TS, and ε-TS. It provides an empirical basis for the selection of algorithms for the MAB problem in this context, and also provides a new perspective for algorithm design and optimization in complex environments. By studying the advantages and disadvantages of various TS-type algorithms, researchers can use these algorithms to solve practical problems more efficiently.

2. Methodology

2.1. UCB Algorithm

The UCB algorithm is a classic algorithm for solving the MAB problems. Its purpose is to balance the contradiction between exploration and exploitation. In MAB problems, agents need to choose among multiple options, and the payoff of each option is unknown and uncertain. The UCB algorithm introduces a confidence bound to help decision-makers choose options that have both higher expected rewards and greater uncertainty, thereby optimizing long-term benefits [13].

The UCB algorithm will first "explore" all arms of the multi-armed slot machine and obtain the corresponding reward data by selecting each option once. The upper confidence bound index is calculated for each option, and this upper confidence bound index is determined by the current average reward and exploration reward of the option. The formula for the confidence upper bound index is usually expressed as:

\( UC{B_{i}}(t-1)={\hat{μ}_{i}}(t-1)+{(\frac{2ln{t}}{{T_{i}}(t-1)})^{\frac{1}{2}}}\ \ \ (1) \)

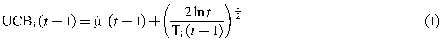
In equation (1), the first term represents the average reward of option i in the past t-1 rounds, t represents the current round number and represents the number of times option i was selected in the past t-1 rounds. At each decision, the UCB algorithm selects the option with the largest confidence upper bound index. This method ensures that the options that currently appear to perform best are frequently selected, while also allowing less certain options to have a chance to be explored, thereby achieving a sub-linear growth of cumulative regret.

1.1. TS Algorithm

The TS algorithm is a Bayesian method widely used in Multi-Armed Bandits problems. Its core idea is to sample according to the posterior distribution of rewards and select the optimal action based on the sample value to maximize long-term benefits [9]. TS represents the return rate of each action with a probability distribution, which we usually call the prior distribution. First, sample from the prior distribution of all actions and perform Bayesian update. At each decision, the TS algorithm samples from the posterior distribution of each action and selects the action with the highest sample value. The Bernoulli distribution discussed in this article has the Beta distribution as a conjugate prior, which is easy to do Bayesian update [9]. Over time, the algorithm adjusts the degree of trust in different actions by updating these probability distributions. In the initial stage, the return rate distribution of all actions is the same. Each time an action is selected, and its return is observed, the algorithm updates the return rate distribution of the action to make it closer to the true distribution. After multiple selections and updates, the TS algorithm can gradually identify actions with higher return rates. Beta distribution is a continuous distribution defined on the interval [0,1]. The probability density functions of Beta distribution and 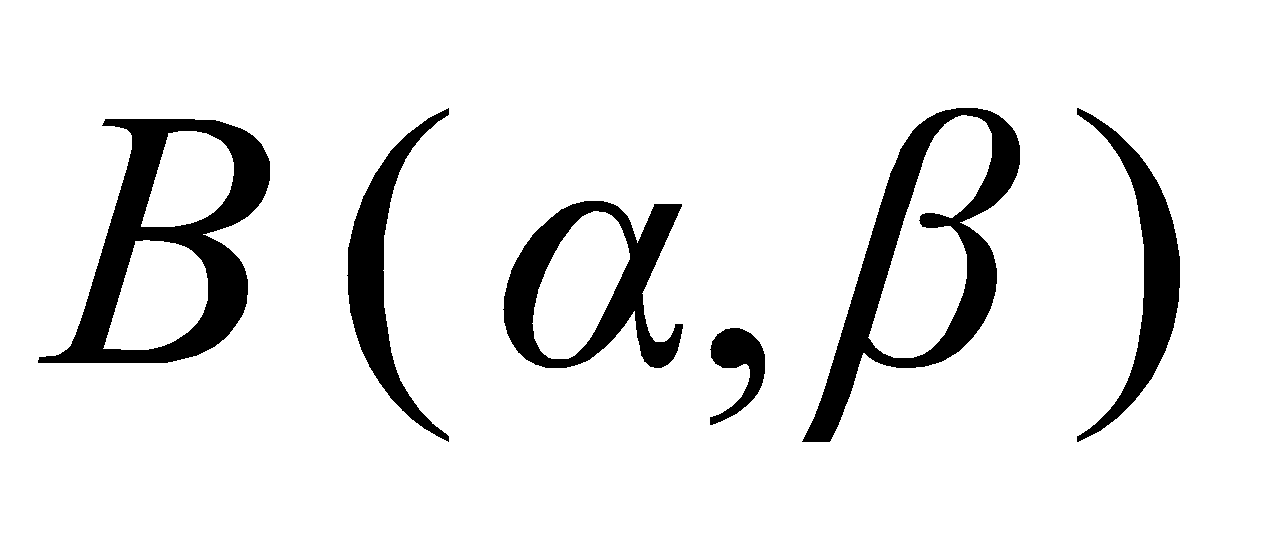are shown in equation (2):

1.2. ε-TS Algorithm

ε-Greedy algorithm and TS are two different MAB algorithms. The ε-TS Algorithm in this study combines the two. Set a small ε, here set to 0.1. Generate a random number, when it is greater than ε, use Thompson Sampling to select the arm, otherwise randomly select an arm for exploration. ε will decay over time, that is, 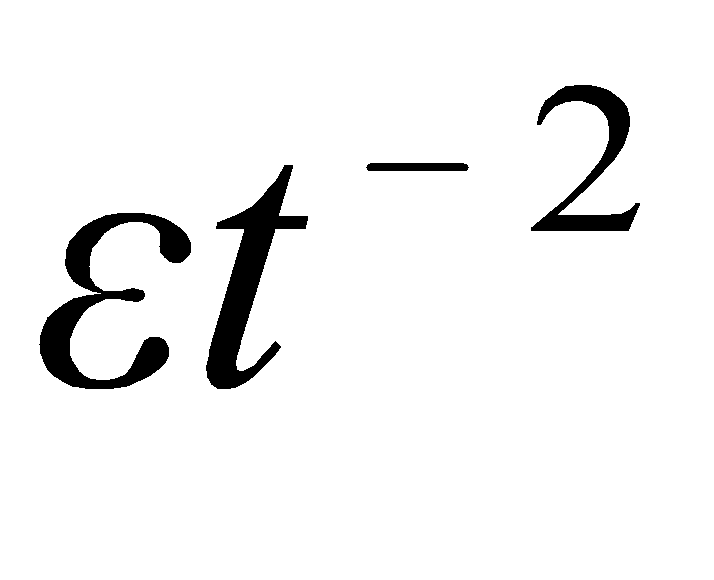, because over time, the confidence in each arm is gradually accumulated, and it should be used more instead of too much exploration, reducing unnecessary exploration.

2. Experimental Design

When designing the simulation experiment, to minimize randomness and enhance the accuracy of the results, experiments were conducted under varying conditions, including different numbers of arms and rounds. Use R software to design and simulate the Multi-Armed slot machine and initialize the basic parameters of the multi-armed slot machine model. In this experiment, it is assumed that the reward of each arm of the Multi-Armed slot machine follows the Bernoulli distribution. By modifying the number of arms (k) and the number of rounds of the experiment, calculate the cumulative regret under the corresponding parameter conditions. By comparing the size of the cumulative regret of each algorithm in the experiment, compare their performance. Since we know the expected cumulative reward of the best arm, the calculation formula for cumulative regret is:

In equation (3), 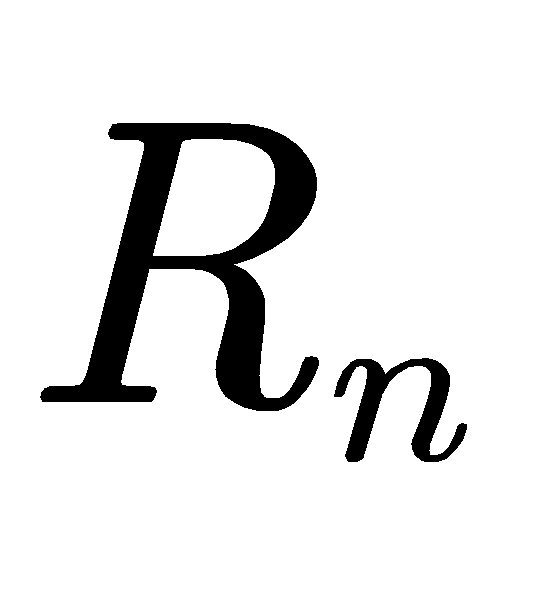represents regret over n rounds, 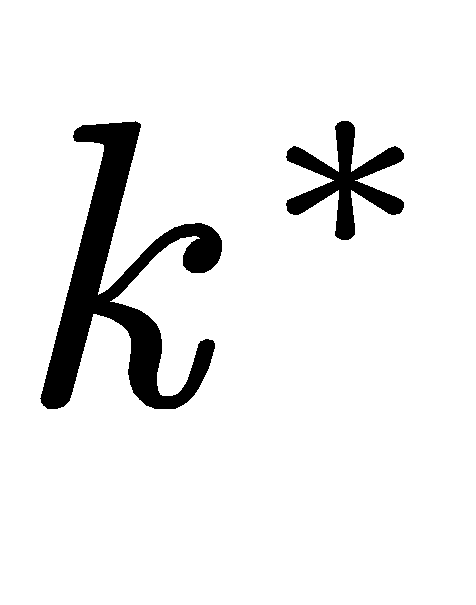is the optimal arm, 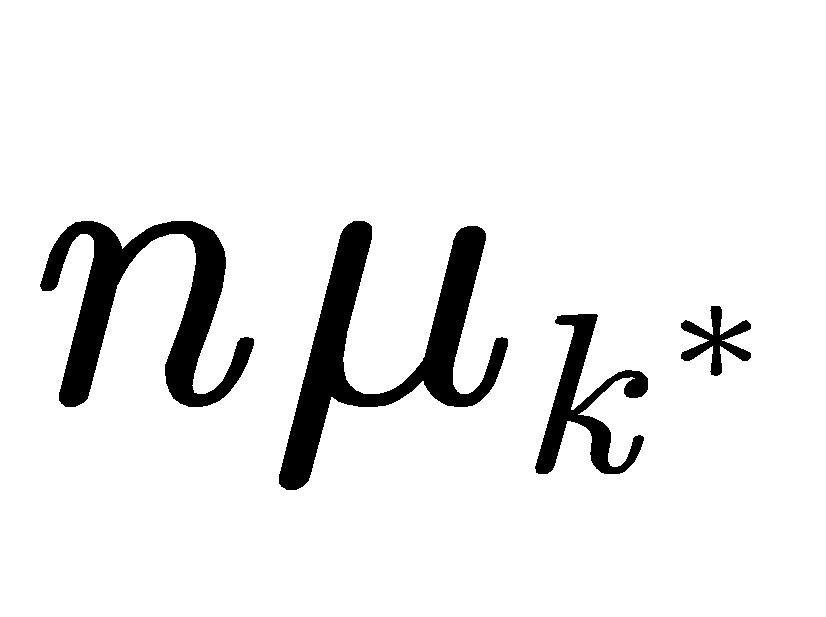represents the expected cumulative reward of the best arm, and the second term of the equation is the expected cumulative reward of our policy.

2.1. Performance comparison of UCB, TS and ε-TS

Experiment 1: Set k=5, and include three sub-experiments, with the number of rounds of the sub-experiments being 1000, 10000, and 100000 respectively. In each sub-experiment, each algorithm runs the specified number of rounds as one time, and all three algorithms run 100 times. Calculate the average value of the cumulative regret of the 100 experiments as the cumulative regret of the sub-experiment. Comparing the cumulative regret, the algorithm with a larger cumulative regret performs worse.

Experiment 2: Set k=8, and include three sub-experiments, with the number of rounds of the sub-experiments being 1000, 10000 and 100000 respectively. In each sub-experiment, each algorithm runs the specified number of rounds once, and all three algorithms run 100 times. Calculate the average value of the cumulative regret of the 100 experiments as the cumulative regret of the sub-experiment. Comparing the cumulative regret, the algorithm with a larger cumulative regret performs worse.

2.2. Performance comparison of TS and ε-TS

Experiment 3: Set k=5, including three sub-experiments, and the number of rounds of the sub-experiments is 1000, 10000 and 100000 respectively. In each sub-experiment, each algorithm runs the specified number of rounds as once, and both algorithms run 100 times. Calculate the average value of the cumulative regret of the 100 experiments as the cumulative regret of the sub-experiment. Finally, compare the cumulative regrets as in Experiments 1 and 2.

Experiment 4: Set k=8, including three sub-experiments, and the number of rounds of the sub-experiments is 1000, 10000 and 100000 respectively. In each sub-experiment, each algorithm runs the specified number of rounds as once, and both algorithms run 100 times. Calculate the average value of the cumulative regret of the 100 experiments as the cumulative regret of the sub-experiment. Finally, compare the cumulative regrets.

Experiment 5: Set k=15, including four sub-experiments. Compared with experiments 3 and 4, the exploration space is expanded, and the number of rounds of sub-experiments is set to 1000, 10000, 100000 and 1000000 respectively. In each sub-experiment, each algorithm runs the specified number of rounds once, and both algorithms run 100 times. The average value of the cumulative regret of the 100 experiments is calculated as the cumulative regret of the sub-experiment. Finally, the cumulative regret is compared.

3. Results and Discuss

3.1. Experiment 1 and 2

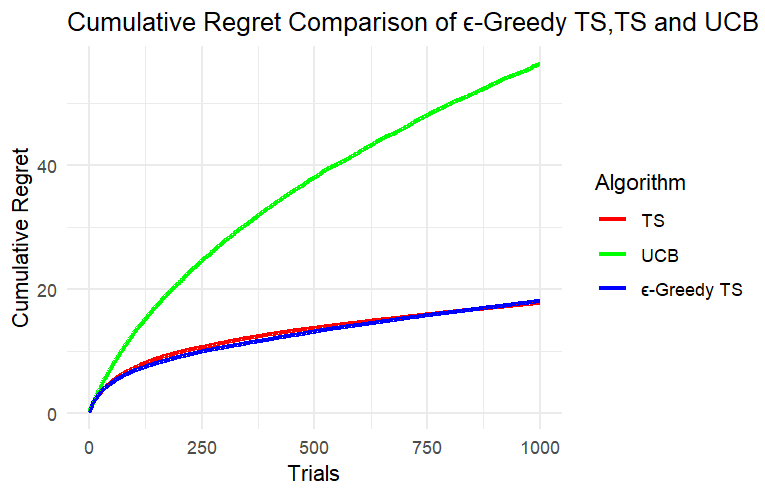
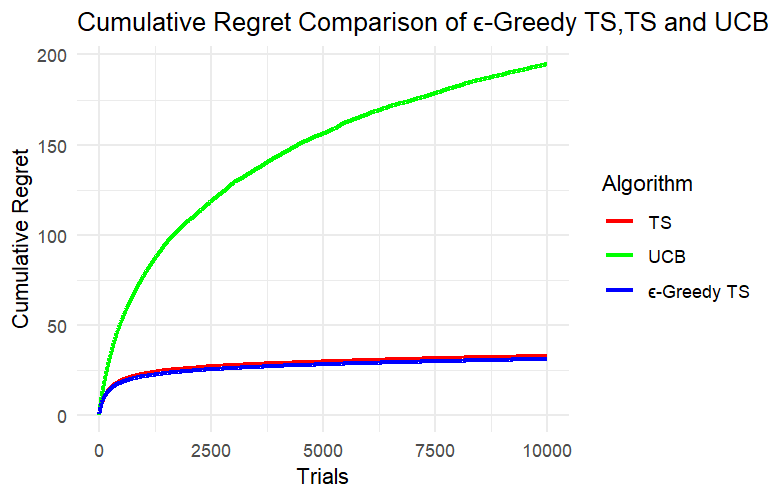
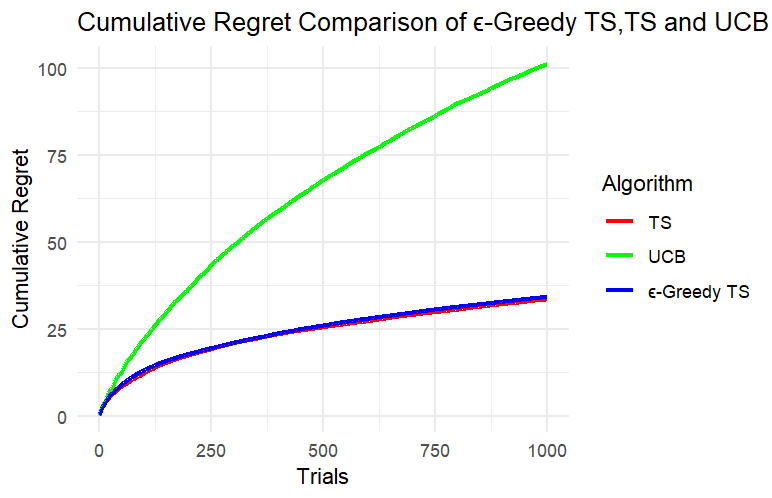
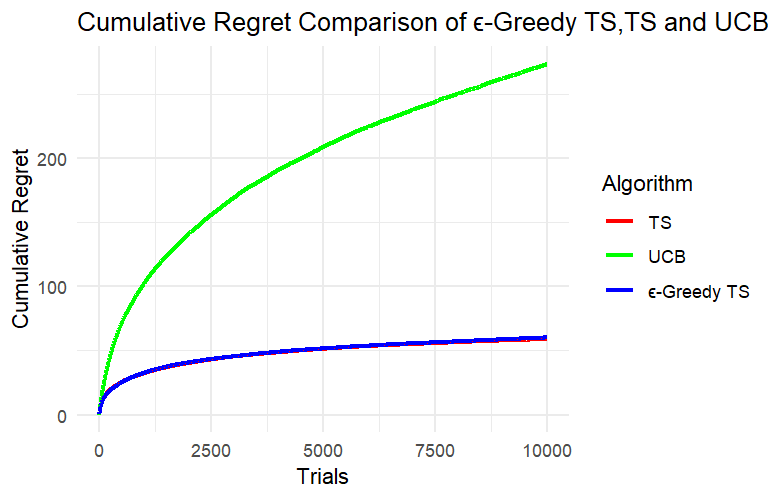
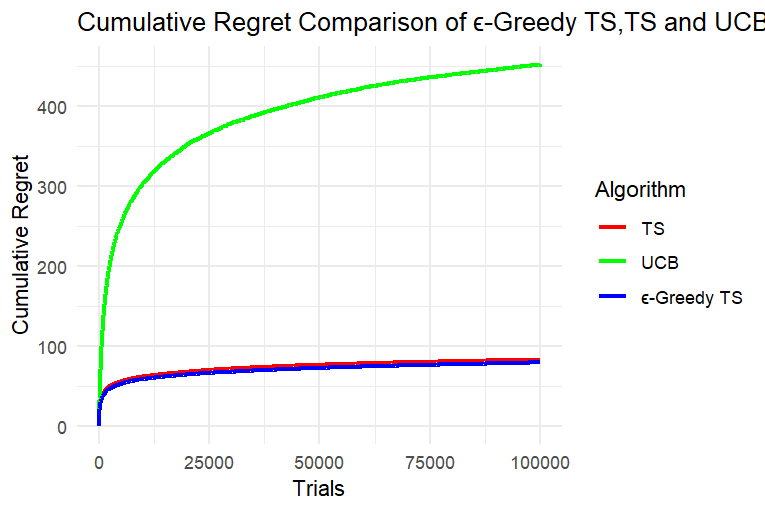
According to Figure 1, (A), (B) and (C) are the experimental results when k=5, and (a), (b) and (c) are the experimental results when k=8.

(A) (B)

(C) (a)

(b) (c)

Figure 1. Results of Experiment 1 and Experiment 2

Through the results of Experiment 1 and Experiment 2, we can clearly see that in this simulated slot machine model, after setting different numbers of arms and experimental rounds, the cumulative regret of the UCB algorithm reaches more than three times that of the other two algorithms after a period of operation and performs the worst in this model. Since the cumulative regret of the UCB algorithm in the two experiments is much greater than the cumulative regret of the other two algorithms, it is not conducive to analyzing the cumulative regret curves of the three algorithms together. Next, we can only analyze TS and ε-TS, which have similar performance when dealing with this problem.

3.2. Experiment 3, Experiment 4 and Experiment 5

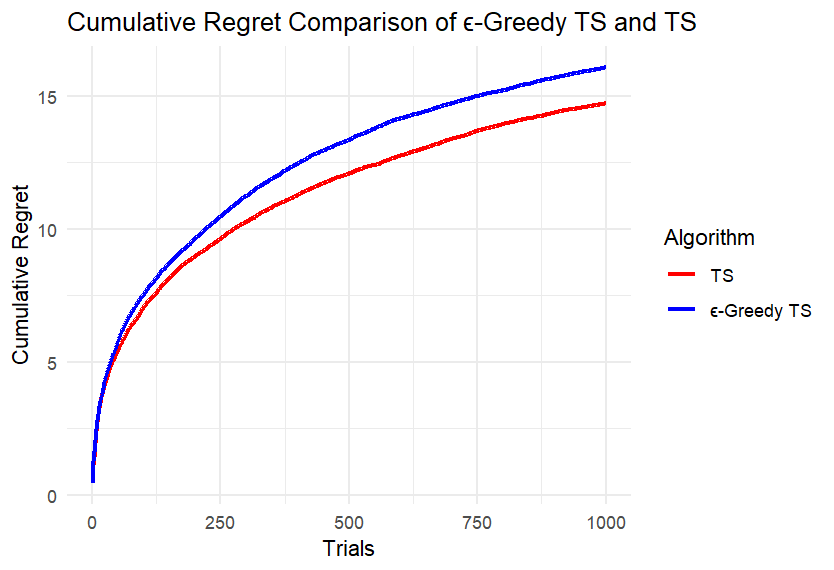
According to the visualized curves Figure 2 and Figure 3, (d), (e) and (f) are the experimental results when k=5; (g), (h) and (i) are the experimental results when k=8; (j), (k), (l) and (m) are the experimental results when k=15.

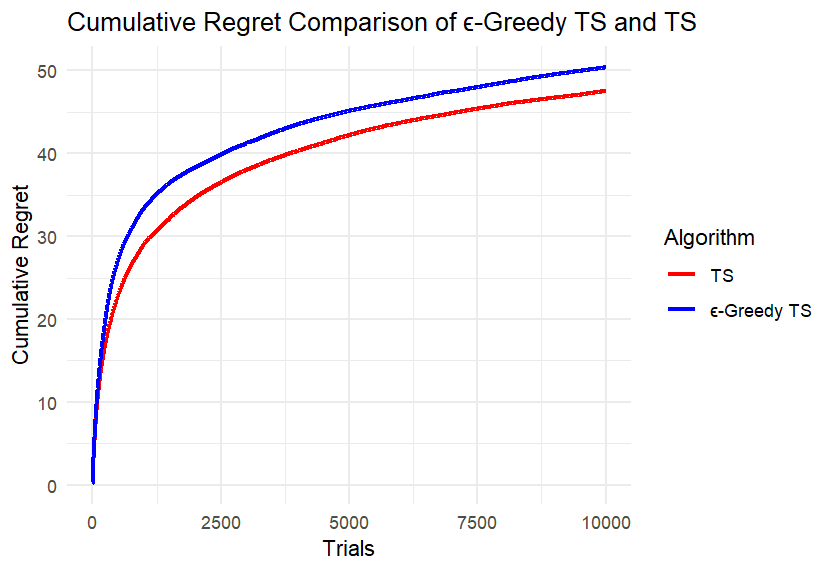
(d) (e)

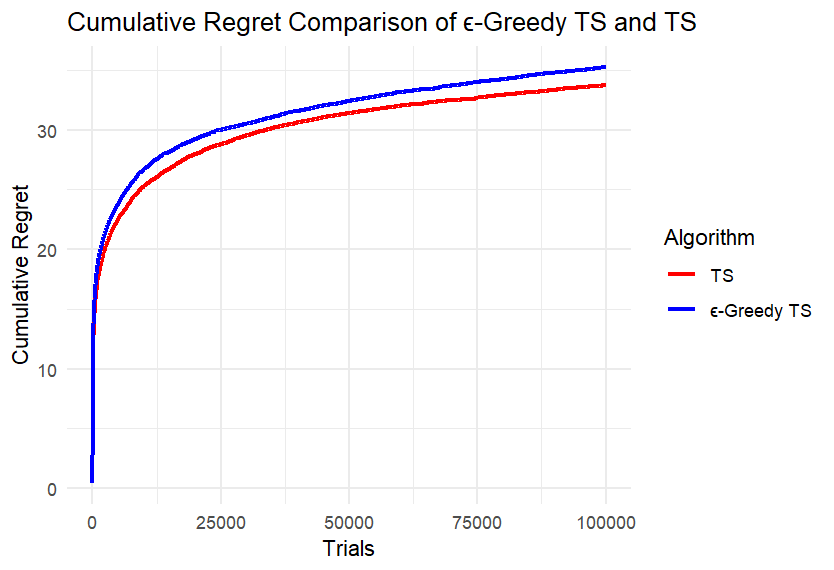
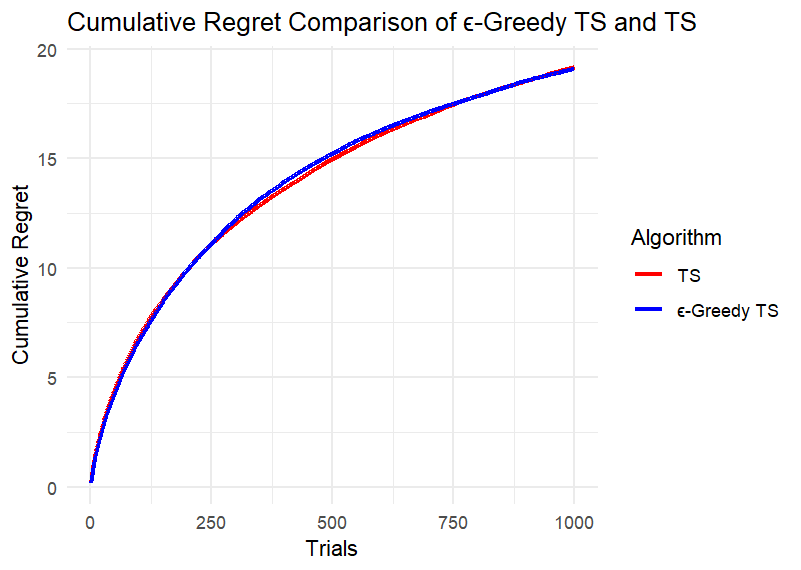
(f) (g)

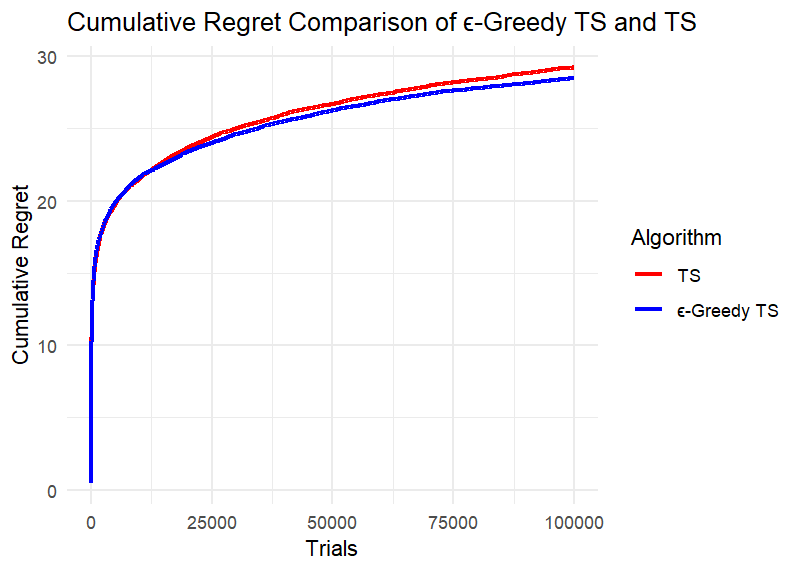
(h) (i)

Figure 2. Results of Experiment 3 and Experiment 4

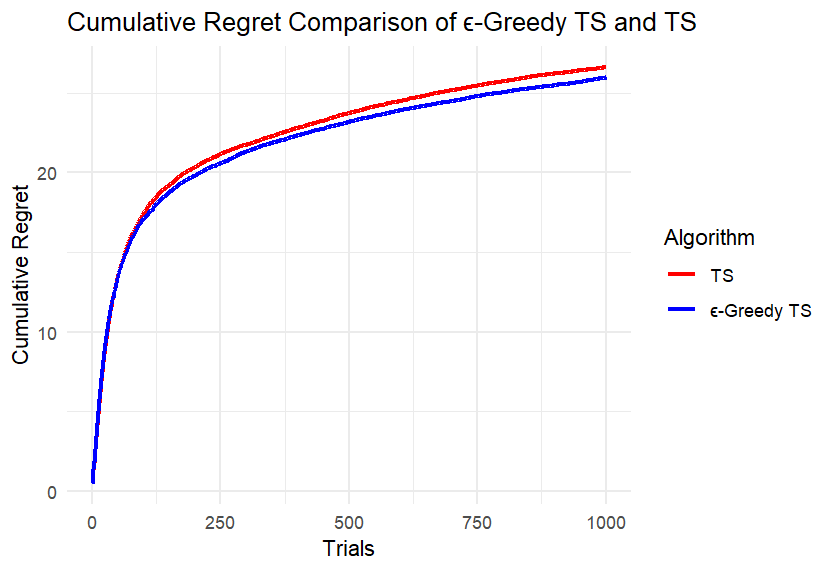
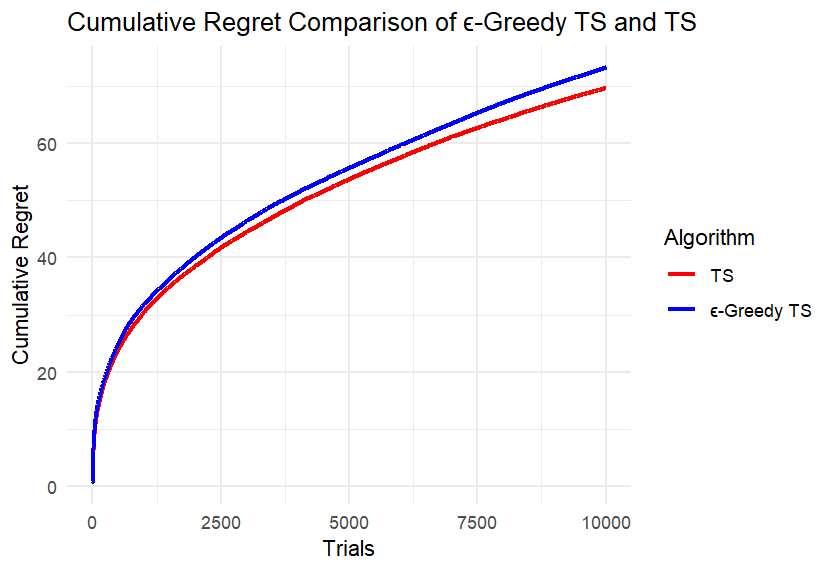
(j) (k)

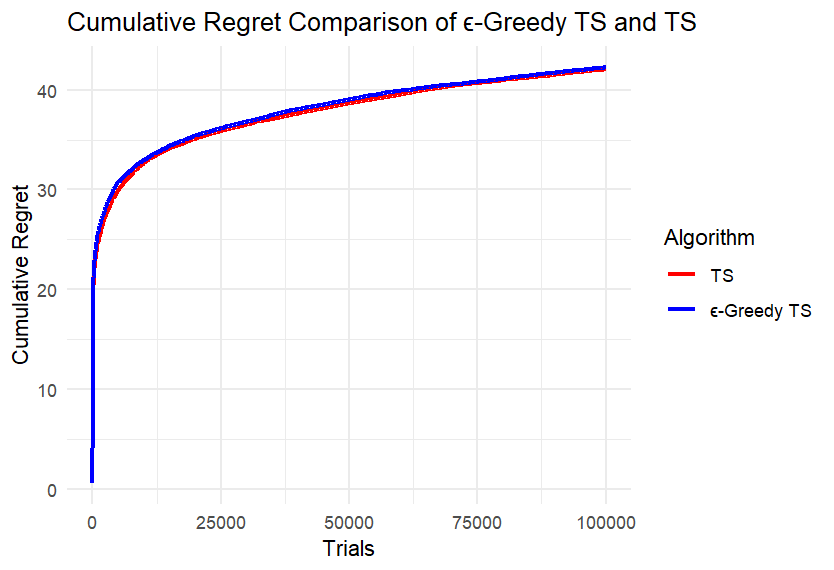
(l) (m)

Figure 3. Results of Experiment 5

We can first intuitively find that the difference between the two algorithms is not large. Take four points equally spaced along the x-axis of each image, record the cumulative regret values of the two algorithms at these points, and calculate the difference, retaining two decimal places. Record the maximum difference in each image in the table below. Calculate the ratio of each difference to the corresponding larger cumulative regret value and also record it in the Table 1.

Table 1. Difference Analysis of Cumulative Regret

According to Table 1, under different conditions of k and n, the ratio of the maximum difference of the cumulative regret of the two algorithms to the corresponding larger cumulative regret is mostly less than 5%; only when k is small and the number of rounds is small, the difference is slightly larger, and the ratio does not exceed 14%. This is because at the beginning, the ε-TS Algorithm will explore more than TS, and the regret may be larger. When the total number of rounds is small, the operation of the algorithm is not yet stable.

3.3. Efficiency of the Algorithm

In addition, we analyze the performance difference between the two algorithms from the perspective of efficiency. Table 2 records the actual time it takes for the two algorithms to run once when the number of rounds is n and k is 8.

Table 2. Difference Analysis of Cumulative Regret

According to Table 2, under the experimental conditions, the number of algorithm rounds increased by 10 times, and the running time almost increased by 10 times. If the total number of rounds is required to be very large, there will be a significant difference in the running efficiency of the two algorithms.

4. Conclusion

This study evaluated the performance of the UCB algorithm, TS algorithm and ε-TS algorithm in the context of a simulated multi-armed bandit machine with Bernoulli distribution through theoretical analysis and simulation experiments. Unlike previous studies, this paper introduces a custom-defined ε-TS algorithm, developed based on the characteristics of the TS and ε-greedy algorithms, as well as the original ε-TS algorithm. This custom ε-TS algorithm is employed in the comparative analysis.The results of the study showed the differences in the performance of the three algorithms. TS algorithms (TS and ε-TS) have better performance in finding the optimal choice due to their higher randomness. After running for a period of time under the multiple parameter conditions set by the study, the cumulative regret of the UCB algorithm is more than three times the cumulative regret of the TS algorithm.

From the perspective of minimizing cumulative regret, the ε-TS algorithm has a mechanism for making random choices with a certain probability compared to the TS algorithm, which has higher flexibility. However, determining an appropriate value for ε is a significant challenge. The algorithm will explore more and may produce more regrets in some exploration processes. This study shows that in the simulated multi-armed bandit problem where the reward follows the Bernoulli distribution, the cumulative regrets of the two algorithms are extracted, and the ratio of their difference to the larger cumulative regret is basically no more than 5%, which shows that when dealing with this problem, the difference between TS and ε-TS is very small. However, from the perspective of algorithm efficiency, the TS algorithm uses the current Bayesian posterior information to make decisions at each selection, making each selection optimal, or at least suboptimal. However, the ε-TS makes random selections under the ε probability, and this randomness introduces a certain degree of inefficiency, especially when a large amount of data has been accumulated and a relatively accurate estimate of the reward distribution has been made. This inefficiency is particularly obvious. Research shows that when the number of algorithm rounds increases by m times, the algorithm running time will also increase by m times; when the total number of rounds is large, the operating efficiency of TS will be much higher than that of ε-TS. So overall, in this multi-armed bandit model, it is wiser to choose the TS algorithm.

Due to the constraints of computational power, the total number of rounds for each experiment and the number of repetitions to accurately determine cumulative regret are limited, which may affect the accuracy of the results. At the same time, the study was carried out in the environment of a simulated multi-armed bandit whose rewards follow a Bernoulli distribution, and further exploration is needed for other reward distributions. In the future, we can further explore the performance of these three algorithms in the MAB problem when the reward distribution follows a Gaussian distribution; we can also focus our research on optimizing the ε-TS algorithm. This study uses the ε-TS algorithm as a basic method, and we can further explore the scientific setting of ε and the design of the algorithm and improve the algorithm's ability to minimize cumulative regret through optimization; or, we can apply the explored model to actual scenarios, such as using TS algorithms to solve advertising delivery problems.