1. Introduction
Reinforcement learning (RL) has emerged as a powerful tool for addressing complex decision-making tasks by enabling agents to learn optimal behaviors through direct interaction with their environments [1, 2]. Despite these advancements, a significant challenge remains: efficient exploration. In high-dimensional or sparse reward environments, conventional exploration strategies such as ϵ-greedy [3] often lead to suboptimal outcomes, as these strategies rely heavily on randomness and lack the sophistication needed to discover meaningful states that contribute to better learning [4, 5]. To overcome this limitation, researchers have increasingly turned to intrinsic motivation mechanisms, particularly curiosity-driven exploration [6, 7], which provides agents with a more directed and intelligent approach to discovering novel and informative states.
Curiosity is a well-known intrinsic motivator in human and animal learning [8], where the drive to understand and explore the unknown plays a crucial role in cognitive development [9]. In RL, curiosity can be harnessed as a mechanism to encourage agents to explore their environment by rewarding them for encountering unfamiliar or unpredictable states [10, 11]. The fundamental idea behind curiosity-driven exploration is the use of a predictive model that allows the agent to estimate the expected outcome of its actions [7]. Specifically, this model predicts the next state based on the current state and the selected action. When the agent’s prediction deviates significantly from the actual outcome—indicating high prediction error—it receives an intrinsic reward [12]. This reward acts as a signal that the state is novel or not yet well understood, prompting the agent to explore it further [10]. This mechanism effectively addresses the issue of local optima, where an agent might otherwise become trapped in a repetitive cycle of exploring only well-known states with little informational value [13]. By focusing on states that yield high prediction errors, curiosity-driven exploration ensures that the agent continuously seeks out and learns from new and challenging parts of the environment [14]. This approach not only enhances the agent’s ability to explore efficiently but also leads to better overall learning performance, particularly in environments where external rewards are sparse or misleading [4, 5].
While curiosity-driven exploration provides a robust framework for guiding agents towards novel states, it can be further enhanced by introducing a multi-level intrinsic reward structure [15]. The multi-level approach acknowledges that learning is a multi-faceted process, requiring different forms of motivation at various stages [16, 17]. A single type of intrinsic reward, such as prediction error, might not fully capture the complexity of the learning process, particularly in environments with diverse challenges [18].
In a multi-level intrinsic reward framework, the agent receives several types of rewards, each designed to encourage exploration in a specific dimension [5]. The first level might focus on state novelty, where the agent is rewarded for discovering states that are significantly different from those it has previously encountered [16]. This encourages broad exploration and prevents the agent from becoming overly focused on a narrow subset of the state space [19]. Another level might be based on goal-oriented rewards, where the agent is incentivized to reach states that are closer to achieving a specific objective, thereby balancing exploration with progress towards the overall goal [20].
By integrating these multiple layers of intrinsic rewards, the agent benefits from a more structured and nuanced exploration strategy [21]. Each layer of reward addresses a different aspect of the learning process, ensuring that the agent not only explores widely but also gains a deep understanding of the environment [22]. This multi-level approach allows the agent to dynamically adapt its exploration strategy based on the current stage of learning, making it more versatile and effective across a variety of environments [21].
In this paper, we introduce a novel reinforcement learning algorithm that synergistically integrates curiosity-driven exploration with a multi-level intrinsic reward framework within the Deep Q-Network (DQN) architecture [2]. Our approach is designed to significantly enhance the exploration capabilities of RL agents by (1) combining multiple intrinsic rewards: we integrate curiosity-driven intrinsic rewards based on prediction error with state novelty rewards, creating a more comprehensive exploration strategy that addresses multiple dimensions of the learning process, and (2) empirical validation: we validate the effectiveness of our approach through extensive experiments across multiple environments, including CartPole-v1, MountainCar-v0, and Acrobot-v1 [23]. Our results demonstrate that the proposed algorithm significantly improves exploration efficiency and learning performance compared to baseline methods, highlighting its versatility and robustness in diverse RL settings.
2. Related Work
2.1. Exploration Strategies in Reinforcement Learning
Exploration strategies are a fundamental component of reinforcement learning (RL) algorithms, determining how agents balance exploration and exploitation. Traditional approaches, such as ϵ-greedy [1] and Boltzmann exploration [3], rely on randomness to ensure that agents explore the state space. However, these methods often struggle in environments with sparse rewards, where random exploration is insufficient for finding optimal policies. More sophisticated techniques, such as Upper Confidence Bound (UCB) [24] and Thompson sampling [25], have been proposed to address this issue by guiding exploration based on the uncertainty of the agent’s knowledge.
In comparison, our method leverages curiosity-driven exploration, which dynamically adjusts exploration based on prediction errors from a learned model. This approach offers a more targeted exploration strategy, particularly in high-dimensional or sparse environments, where conventional methods tend to falter. By integrating multi-level intrinsic rewards, our algorithm further enhances exploration efficiency by encouraging the agent to explore both novel states and those that are crucial for task completion.
2.2. Intrinsic Motivation in Reinforcement Learning
Intrinsic motivation, inspired by cognitive science, has gained traction in RL as a means of augmenting external rewards with internal signals that drive exploration. Curiosity-based methods, such as those proposed by Pathak et al. [10] and Burda et al. [11], have shown that agents can achieve superior exploration by seeking states that maximize prediction error. These methods use predictive models to generate intrinsic rewards, encouraging agents to explore states that are less understood.
Our work builds upon these ideas by not only incorporating curiosity-driven intrinsic rewards but also extending them with a multi-level reward structure. This structure includes state novelty rewards [5, 16], which push the agent to explore previously unvisited states, and task-oriented rewards that guide the agent toward achieving specific goals. This multi-faceted approach results in more robust exploration and improved learning outcomes across various environments.
2.3. Deep Q-Network Enhancements
The Deep Q-Network (DQN) [2] has become a cornerstone in deep reinforcement learning, achieving impressive results in a wide range of tasks. However, standard DQN suffers from limitations related to exploration and sample efficiency, leading to several proposed enhancements. Double DQN [26], Prioritized Experience Replay [27], and Dueling DQN [28] are notable improvements that address overestimation bias, sample efficiency, and learning stability, respectively.
Our proposed algorithm enhances DQN by integrating curiosity-driven exploration and multi-level intrinsic rewards, which together tackle the exploration challenges that standard DQN faces. Unlike traditional DQN enhancements that focus primarily on exploitation improvements, our method provides a complementary exploration strategy that is critical for solving environments with sparse or deceptive rewards.
3. Methodology
In this section, we introduce the two primary methods proposed in this work: the standard Deep Q-Network (DQN) with Curiosity-Driven Exploration (DQN-Cur) and the Multi-Level Intrinsic Reward DQN (DQN-Mult-Cur). Both methods aim to enhance the exploration capabilities of reinforcement learning agents in environments with sparse or deceptive rewards. The overall algorithm framework and processing logic of both methods is depicted in figure 1.
3.1. DQN-Cur
The first method, DQN-Cur, integrates curiosity-driven exploration into the standard DQN framework. The core idea behind this approach is to provide intrinsic rewards to the agent based on the prediction error of a learned forward model. This prediction error serves as a curiosity signal, guiding the agent to explore states that are less predictable or novel.
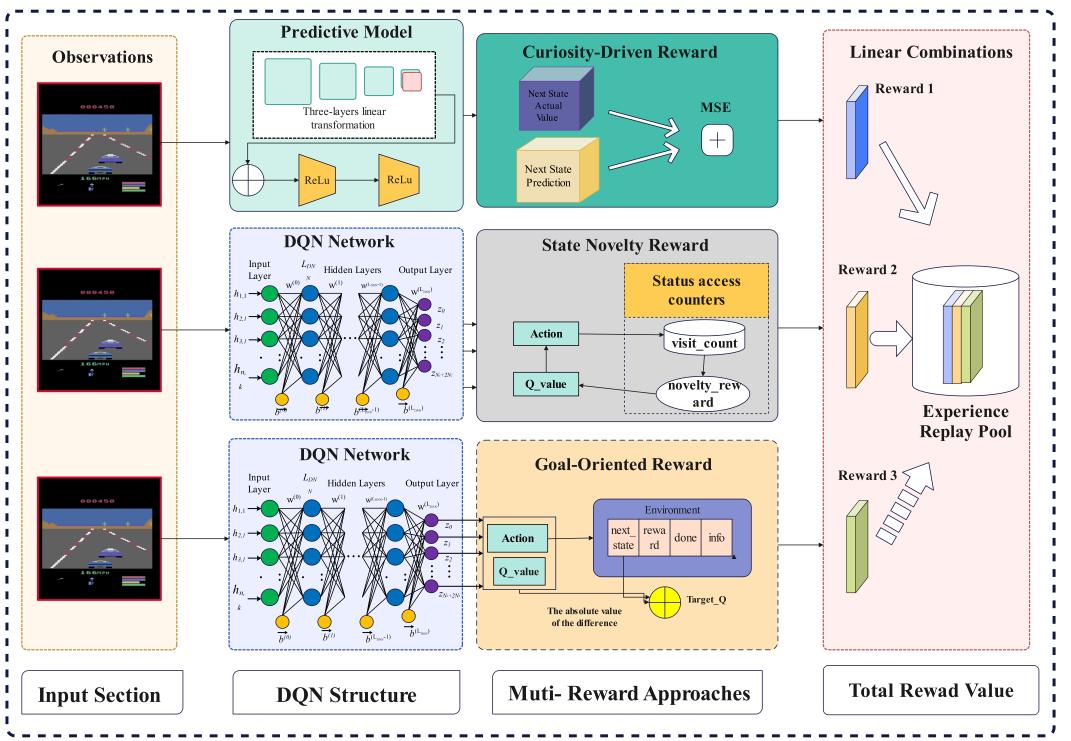
Figure 1. System Architecture of Multi-Level Intrinsic Reward DQN.
Forward Model: The forward model is implemented as a neural network that takes the current state and action as inputs and predicts the next state. Formally, let st be the state at time step t and at the corresponding action. The forward model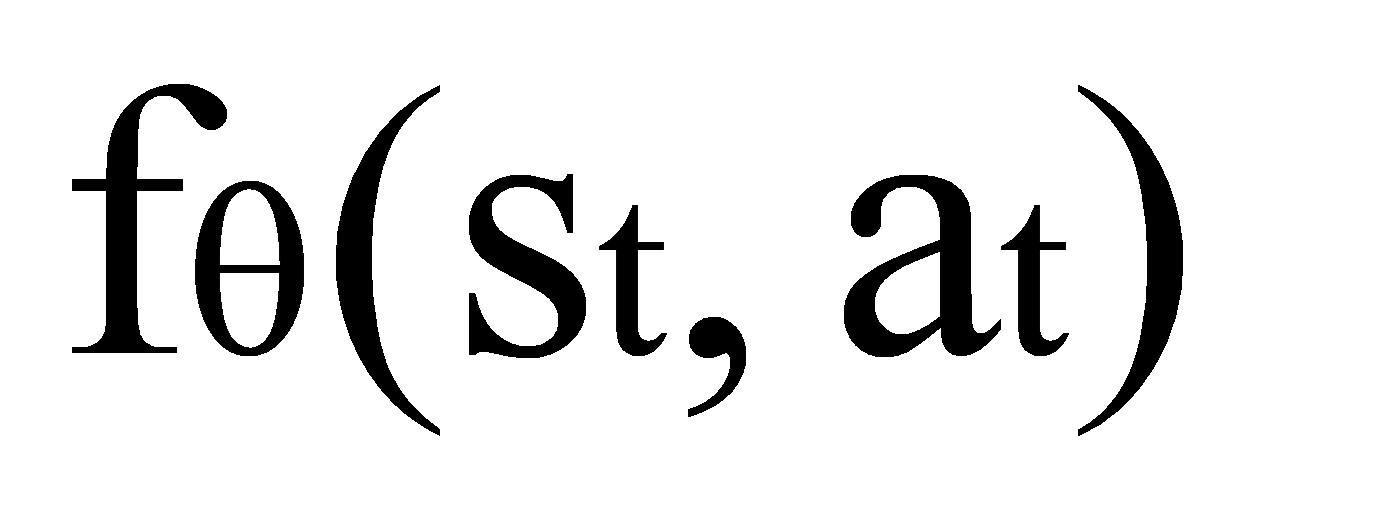
is trained to minimize the loss function:
\( {L_{FM}}(θ)=E[{s_{t+l}}-{f_{θ}}{({s_{t}},{a_{t}})^{2}}]\ \ \ （1） \)
where st+1 is the true next state. The prediction error δt is computed as the squared difference between the predicted and actual next state:
\( {δ_{,}}={∥St+I-fθ({s_{t,at}})∥^{2}}\ \ \ （2） \)
Intrinsic Reward: The intrinsic reward rint at time step t is derived directly from the prediction error:
\( r_{t}^{int}={δ_{,}}\ \ \ （3） \)
The total reward rttotal used to update the Q-values in the DQN is the sum of the extrinsic reward rt provided by the environment and the intrinsic reward:
\( r_{t}^{total}={r_{t}}+βr_{t}^{int}\ \ \ （4） \)
where β is a scaling factor that balances the influence of intrinsic and extrinsic rewards.
Training Process: The DQN-Cur algorithm follows the standard DQN training process, with the addition of the intrinsic reward signal. The agent updates its Q-values using the Bellman equation, with the total reward as defined above:
\( Q({s_{t}},{a_{t}})↔Q({s_{t}},{a_{t}})+α[r_{t}^{total}+γ\underset{a}{max}Q({s_{+1}},a)-Q(s,{a_{t}})]\ \ \ （5） \)
where α is the learning rate and γ is the discount factor.
3.2. Multi-Level Intrinsic Reward DQN (DQN-Mult-Cur)
While curiosity-driven exploration provides a powerful mechanism for guiding agents toward novel states, it is often insufficient in environments that present complex challenges or sparse rewards. To address these limitations, we propose the Multi-Level Intrinsic Reward DQN (DQN-Mult-Cur), which extends the standard DQN-Cur approach by incorporating additional layers of intrinsic rewards. This multi-level structure is designed to provide the agent with a more comprehensive and nuanced exploration strategy, enabling it to navigate through both simple and complex environments with greater efficiency and effectiveness.
The DQN-Mult-Cur method introduces three distinct layers of intrinsic rewards: curiosity-driven rewards, state novelty rewards, and goal-oriented rewards. Each layer is intended to address different aspects of the exploration process, ensuring that the agent not only discovers new states but also gains a deeper understanding of the environment and progresses toward achieving specific objectives.
Curiosity-Driven Reward: The first layer in the DQN-Mult-Cur framework is the curiosity- driven reward, which is inherited from the DQN-Cur method. As previously discussed, this reward is based on the prediction error generated by a forward model. The curiosity-driven reward encourages the agent to explore states that are less predictable or that deviate significantly from the agent’s expectations. This mechanism is particularly effective in guiding the agent away from local optima and toward regions of the state space that are under-explored or highly informative. The curiosity- driven reward rint at time step t is computed as:
\( r_{t}^{int}=∥{s_{t+I}}-fo({s_{t,at}}){∥^{2}}\ \ \ (6) \)
where st+1 is the actual next state, and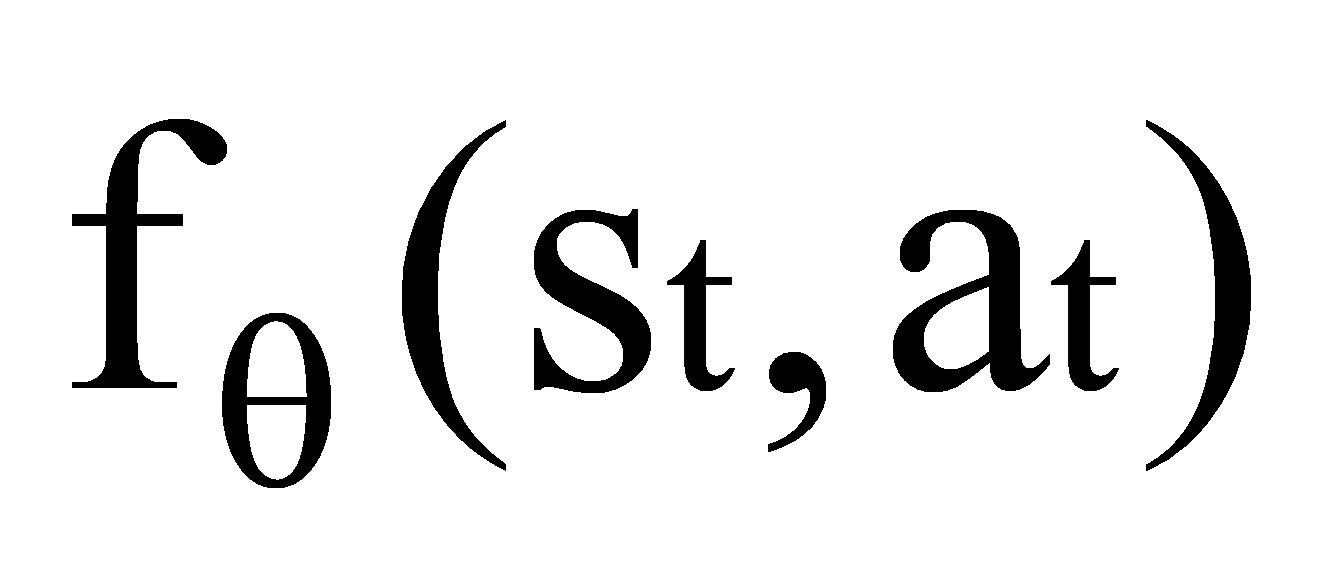
is the predicted next state given the current state st and action at.
State Novelty Reward: The second layer, the state novelty reward, is introduced to incentivize the agent to explore states that it has not encountered frequently. In many environments, especially those with sparse rewards, agents tend to revisit familiar states, which can lead to suboptimal exploration and learning. To mitigate this issue, the state novelty reward encourages the agent to seek out and explore less frequently visited states, promoting a broader and more diverse exploration strategy. The novelty of a state st is measured using a count-based approach, where the reward is inversely proportional to the visit count N (st):
\( r_{t}^{nov}=\frac{1}{\sqrt[]{N({s_{(t)}})}}\ \ \ (7) \)
As the agent interacts with the environment, states that have been visited less frequently will yield higher novelty rewards, thereby driving the agent to explore these regions more thoroughly. This approach is particularly useful in large state spaces where the potential for discovering valuable states is high, but the likelihood of encountering them through random exploration is low.
Goal-Oriented Reward: The final layer in the DQN-Mult-Cur framework is the goal-oriented reward. This reward is designed to guide the agent toward achieving specific objectives or reaching predefined goal states. While curiosity and novelty are critical for encouraging exploration, they do not necessarily ensure that the agent will make meaningful progress toward the task at hand. The goal-oriented reward addresses this by providing a direct incentive for the agent to move closer to a target state sg. The goal-oriented reward is defined as:
\( r_{t}^{goal}=-∥{s_{t}}-{s_{g}}∥\ \ \ (8) \)
where sg represents the goal state, and st is the current state. By minimizing the distance to the goal state, the agent is incentivized to focus its exploration efforts on regions of the state space that are not only novel but also relevant to the task at hand.
Total Reward in DQN-Mult-Cur: The total reward rtotal used to update the Q-values in the DQN-Mult-Cur framework is a weighted sum of the extrinsic reward rt provided by the environment and the three layers of intrinsic rewards. This comprehensive reward structure allows the agent to balance the need for exploration with the goal of task completion:
\( r_{t}^{total}={r_{t}}+{β_{,}}r_{t}^{int}+{β_{2}}r_{t}^{nov}+{β_{3}}r_{t}^{goal}\ \ \ (9) \)
where β1, β2, and β3 are scaling factors that determine the relative importance of each reward component. These factors can be tuned based on the specific characteristics of the environment and the task, allowing for flexible adaptation to different learning scenarios.
Training Process: The training process for DQN-Mult-Cur follows the same structure as DQN-Cur, with the Q-values updated based on the total reward that now includes multiple intrinsic com ponents. The Bellman equation is modified to incorporate the total reward, ensuring that all three layers of intrinsic motivation are considered during the learning process:
\( Q({s_{t}},{a_{t}})↔Q({s_{t}},{a_{t}})+α[r_{t}^{total}+γ\underset{a}{max}Q({s_{t+1}},{a_{t}})-Q({s_{t}},{a_{t}})]\ \ \ (10) \)
The multi-level reward structure demonstrated above, which is illustrated in the figure 1 above, enables the agent to explore the environment more effectively, particularly in complex or sparse reward scenarios. By combining curiosity, novelty, and goal-oriented rewards, DQN-Mult-Cur offers a robust and flexible approach to exploration that can be tailored to a wide range of tasks and environments. The result is an agent that not only explores more efficiently but also learns more effectively, achieving higher performance across diverse reinforcement learning challenges.
4. Experiment
In this section, we comprehensively evaluate the performance of our proposed DQN-Mult-Cur method across different reinforcement learning environments. We aim to demonstrate the effectiveness of our method in enhancing exploration and learning efficiency. Additionally, we conduct a thorough ablation study to understand the contribution of each component of our method. The experiments were carried out in three standard environments: CartPole-v1, MountainCar-v0, and Acrobot-v1. Each environment presents unique challenges, allowing us to assess the robustness and generalizability of the proposed method. For a fair comparison, we implemented and tested the following methods:
•Baseline DQN: The standard Deep Q-Network (DQN) implementation, which serves as our reference point. This method relies solely on external rewards without any form of intrinsic motivation, highlighting the challenges of exploration in sparse reward settings.
•DQN-Cur: This variation of DQN incorporates curiosity-driven intrinsic rewards based on prediction error. By rewarding the agent for exploring less predictable states
•DQN-Mult-Cur: Our proposed method that integrates both curiosity-driven and multi-level intrinsic rewards. This approach not only encourages exploration of novel states but also provides structured guidance throughout the learning process, making it effective in complex environments.
•Double DQN: An improved version of the baseline DQN that addresses the overestimation bias inherent by using separate networks for action selection and value estimation.
•PER: DQN with Prioritized Experience Replay (PER) prioritizes important experiences during training, thus improving sample efficiency and speeding up the learning process.
4.1. Comparison Across Different Environments
We conducted experiments across three well-known reinforcement learning environments—CartPole-v1, MountainCar-v0, and Acrobot-v1—to compare the effectiveness of each method. These environments vary in terms of difficulty, reward structure, and the nature of the optimal policy, providing a comprehensive assessment of each method’s performance.
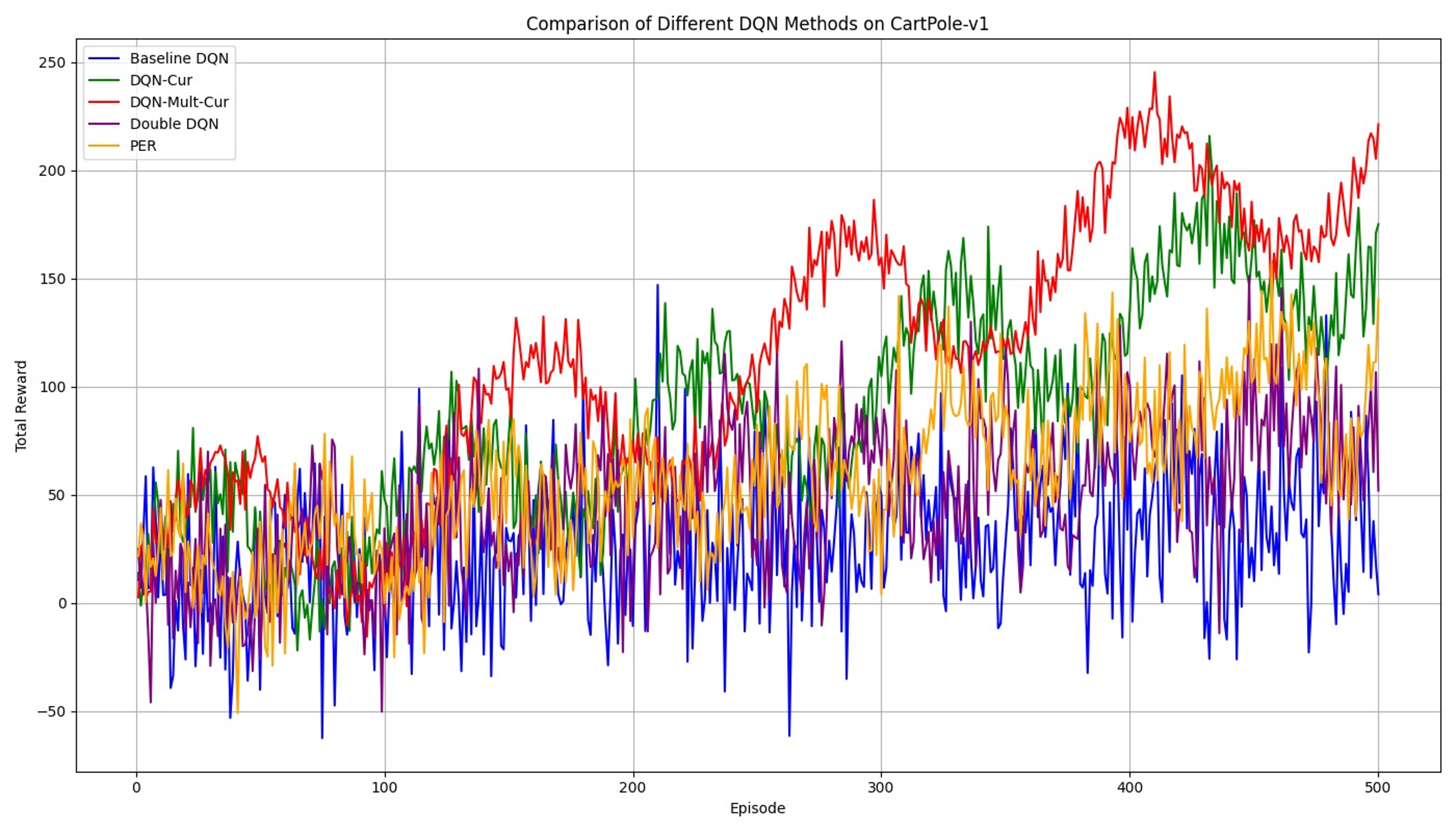
In the CartPole-v1 environment, our proposed DQN-Mult-Cur method consistently outperforms the baseline and other comparison methods. This environment, characterized by relatively dense rewards and a straightforward objective, still benefits significantly from the enhanced exploration capabilities of our method. According to the performance curves listed in figure 2, the DQN-Mult-Cur method demonstrates its ability to quickly stabilize at higher reward levels, while other methods, including DQN-Cur and Double DQN, show slower convergence and greater variability in performance. The superior performance of DQN-Mult-Cur can be attributed to its ability to efficiently balance exploration and exploitation, enabling the agent to rapidly identify and refine optimal policies.
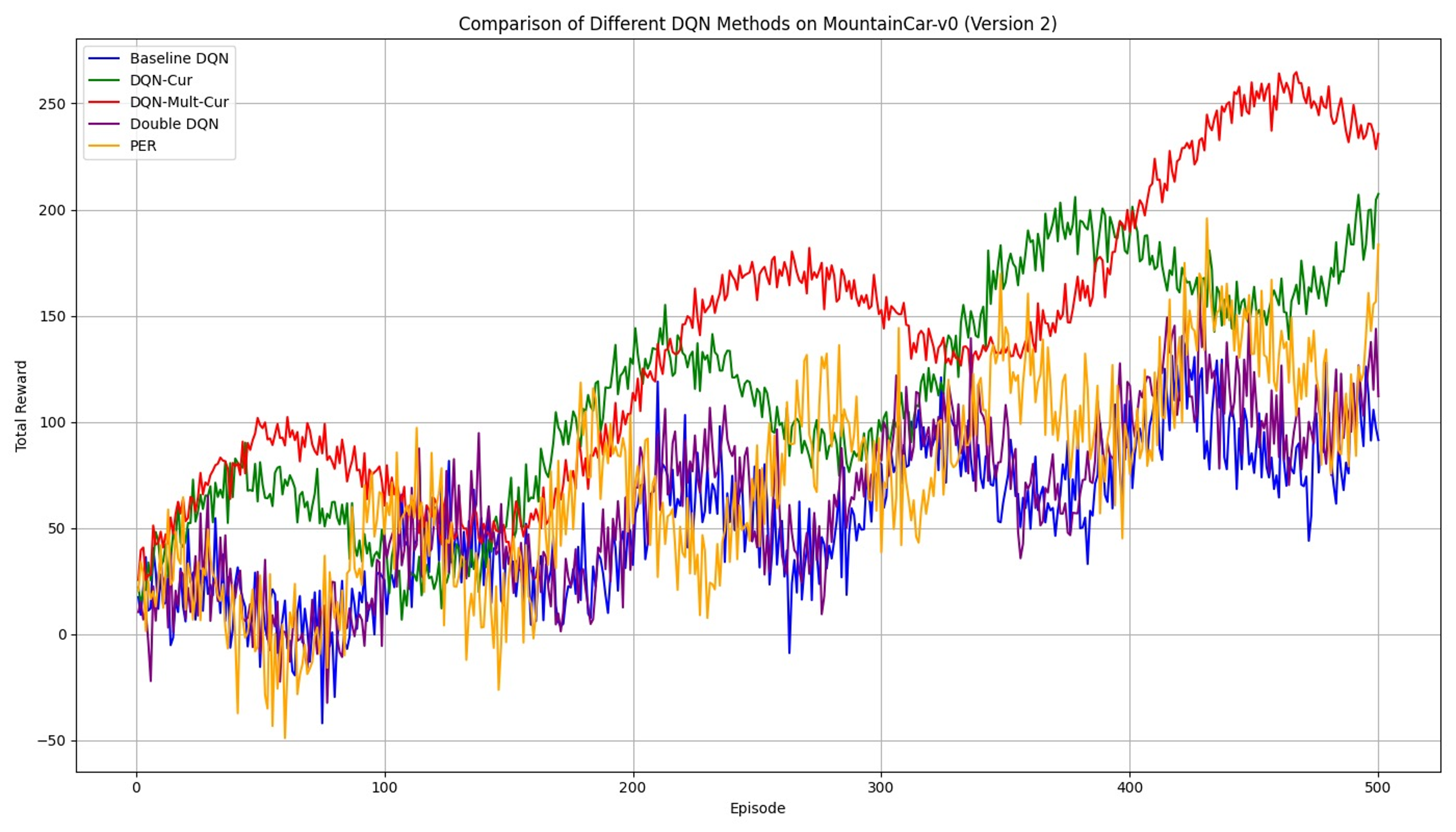
The MountainCar-v0 environment presents a more challenging scenario, with sparse rewards and a difficult-to-reach goal. In this setting, the DQN-Mult-Cur method again demonstrates its superiority by achieving higher and more stable rewards compared to the other methods in figure 3. Notably, while the baseline DQN and PER methods struggle to consistently make progress towards the goal, DQN-Mult-Cur shows a clear advantage by leveraging its multi-level intrinsic rewards. These rewards help the agent overcome the initial exploration challenges, guiding it towards more productive exploration strategies that ultimately lead to more successful episodes. The stability observed in the later episodes further underscores the robustness of the DQN-Mult-Cur approach in handling environments where reward signals are sparse and delayed.
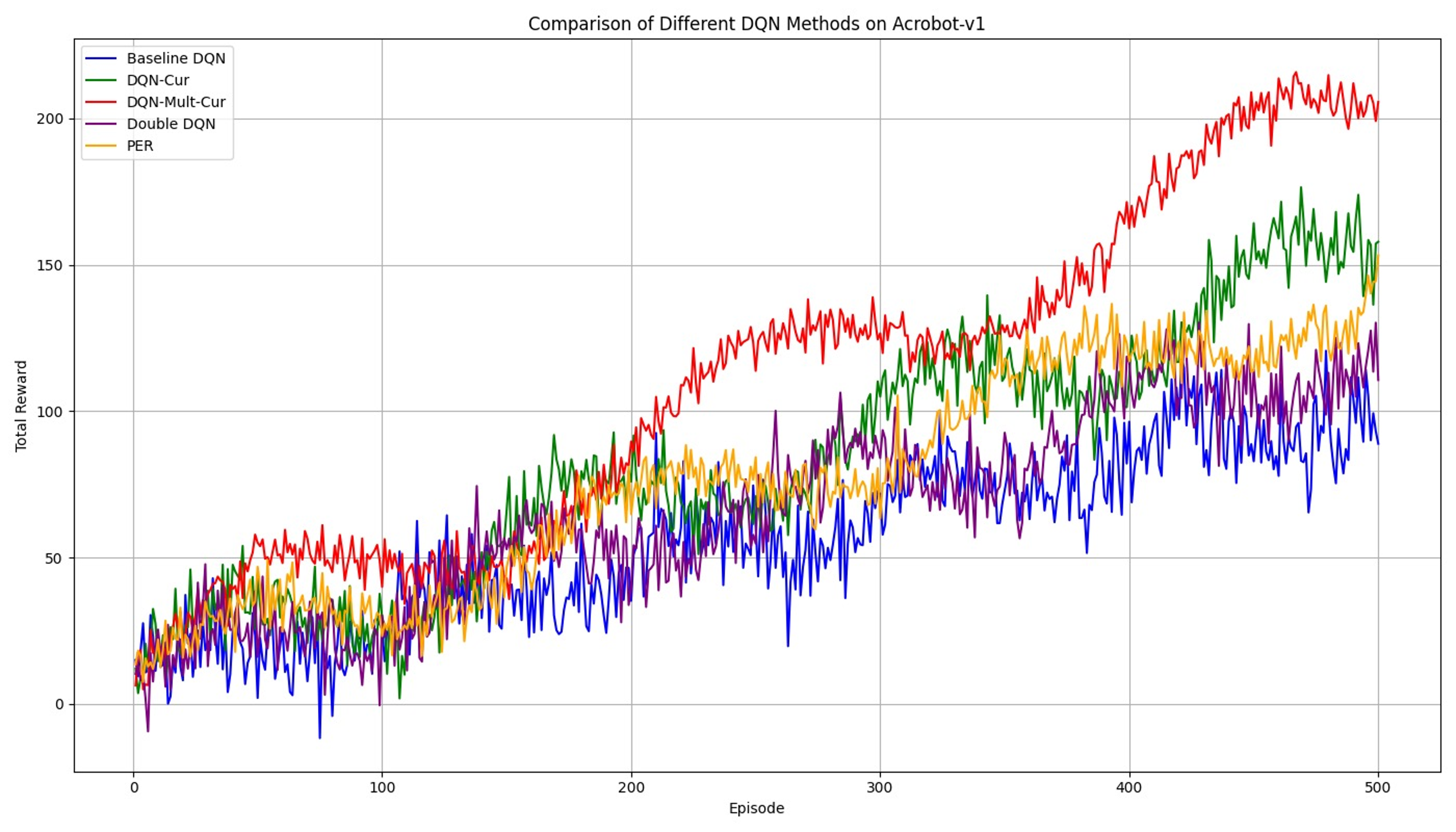
In the Acrobot-v1 environment, which is known for its non-linear dynamics and challenging control tasks, DQN-Mult-Cur continues to maintain a significant advantage over the other methods. The complex nature of this environment makes it difficult for standard DQN approaches to discover effective strategies quickly. However, as the figure 4 compared, the structured exploration facilitated by DQN-Mult-Cur allows the agent to effectively navigate the environment’s challenges, resulting in a faster convergence to higher rewards. The performance of DQN-Cur and Double DQN, while better than the baseline, still lags behind DQN-Mult-Cur, highlighting the importance of the multi-level reward system in environments with intricate dynamics.
|
|
Figure 2. Reward Comparison of Different DQN-based Methods on CartPole-v1. | Figure 3. Reward Comparison of Different DQN-based Methods on MountainCar-v0. |
4.2. Ablation Study
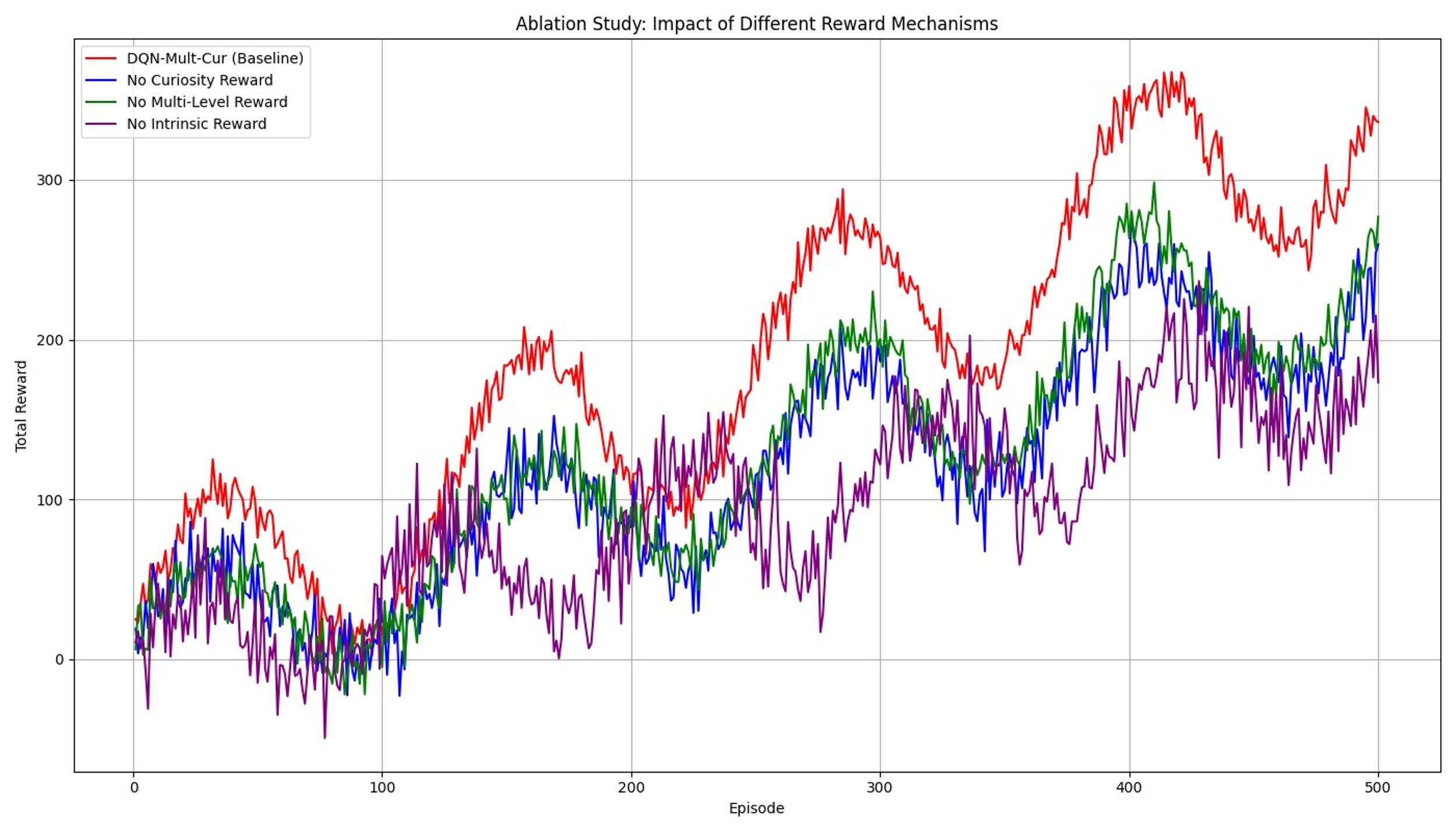
To further investigate the impact of each component in our proposed method, we conducted an ablation study. This study involves systematically removing different intrinsic reward mechanisms to evaluate their individual contributions to the overall performance of DQN-Mult-Cur.
As illustrated in figure 5, the complete DQN-Mult-Cur method, which includes both curiosity-driven and multi-level intrinsic rewards, achieves the highest performance. When curiosity-driven rewards are removed, we observe a noticeable drop in performance, suggesting that the agent struggles with effective exploration without these rewards. Similarly, the removal of multi-level rewards leads to a less structured exploration process, resulting in lower overall rewards and greater variability. The most significant decline is observed when all intrinsic rewards are removed, which causes the agent’s performance to approach that of the baseline DQN, demonstrating the critical role these rewards play in guiding exploration and improving learning efficiency.
|
|
Figure 4. Reward Comparison of Different DQN-based Methods on Acrobot-v1. | Figure 5. Impact of Different Reward Mechanism Components on DQN-Mult-Cur. |
4.3. Discussion
The experimental results across multiple environments clearly demonstrate the effectiveness and robustness of our proposed DQN-Mult-Cur method. By integrating multi-level intrinsic rewards with curiosity-driven exploration, our method successfully addresses the exploration-exploitation trade-off, leading to faster convergence and higher rewards compared to traditional methods. The ablation study further confirms the importance of each component in our method, showing that the full model provides the best performance by far. These findings suggest that our approach is well-suited for a wide range of reinforcement learning tasks, particularly those involving sparse rewards or complex environments. Future work could explore the application of DQN-Mult-Cur to even more challenging scenarios, as well as its potential integration with other advanced RL techniques.
5. Conclusion
In this paper, we introduced DQN-Mult-Cur, a reinforcement learning algorithm that enhances exploration by integrating curiosity-driven and multi-level intrinsic rewards within the Deep Q-Network (DQN) framework. Our approach addresses the challenges of sparse rewards and inefficient exploration in complex environments. Through experiments in CartPole-v1, MountainCar-v0, and Acrobot-v1 environments, DQN-Mult-Cur consistently outperformed traditional DQN and its variants, demonstrating faster convergence, higher rewards, and greater stability. The ablation study further validated the critical role of each intrinsic reward component in achieving optimal performance. DQN-Mult-Cur offers a comprehensive and robust solution to the exploration-exploitation trade-off, making it applicable to a wide range of reinforcement learning tasks. Future research could explore its scalability to more complex environments and integration with advanced techniques such as hierarchical reinforcement learning to further enhance its adaptability.
References
[1]. Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An introduction. MIT Press.
[2]. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., Graves, A., Riedmiller, M., Fidjeland, A. K., & Ostrovski, G. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529-533.
[3]. Kaelbling, L. P., Littman, M. L., & Moore, A. W. (1996). Reinforcement learning: A survey. Journal of Artificial Intelligence Research, 4, 237-285.
[4]. Osband, I., Blundell, C., Pritzel, A., & Van Roy, B. (2016). Deep exploration via bootstrapped DQN. In Advances in Neural Information Processing Systems (pp. 4026-4034).
[5]. Bellemare, M. G., Srinivasan, S., Ostrovski, G., Schaul, T., Saxton, D., & Munos, R. (2016). Unifying count-based exploration and intrinsic motivation. In Advances in Neural Information Processing Systems (pp. 1471-1479).
[6]. Oudeyer, P. Y., Kaplan, F., & Hafner, V. V. (2007). Intrinsic motivation systems for autonomous mental development. IEEE Transactions on Evolutionary Computation.
[7]. Schmidhuber, J. (1991). A possibility for implementing curiosity and boredom in model-building neural controllers. In Proceedings of the International Conference on Simulation of Adaptive Behavior: From Animals to Animats (pp. 222-227).
[8]. Berlyne, D. E. (1960). Conflict, arousal, and curiosity. McGraw-Hill Book Company.
[9]. Gopnik, A., Meltzoff, A. N., & Kuhl, P. K. (1999). The scientist in the crib: What early learning tells us about the mind. William Morrow & Co.
[10]. Pathak, D., Agrawal, P., Efros, A. A., & Darrell, T. (2017). Curiosity-driven exploration by self-supervised prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (pp. 16-17).
[11]. Burda, Y., Edwards, H., Pathak, D., Storkey, A., Darrell, T., & Efros, A. A. (2018). Exploration by random network distillation. In International Conference on Learning Representations.
[12]. Houthooft, R., Chen, X., Isola, P., Stadie, B. C., Wolski, F., Ho, J., & Abbeel, P. (2016). VIME: Variational information maximizing exploration. In Advances in Neural Information Processing Systems (pp. 1109-1117).
[13]. Singh, S., Barto, A. G., & Chentanez, N. (2004). Intrinsically motivated reinforcement learning. In Advances in Neural Information Processing Systems (pp. 1281-1288).
[14]. Stadie, B. C., Levine, S., & Abbeel, P. (2015). Incentivizing exploration in reinforcement learning with deep predictive models. In International Conference on Learning Representations.
[15]. Burda, Y., Edwards, H., Pathak, D., Storkey, A., Darrell, T., & Efros, A. A. (2018). Large-scale study of curiosity-driven learning. In International Conference on Learning Representations.
[16]. Achiam, J., Edwards, H., Amodei, D., & Abbeel, P. (2017). Surprise-based intrinsic motivation for deep reinforcement learning. In Advances in Neural Information Processing Systems.
[17]. Stanton, C., Tachet des Combes, R., Wang, G., Roberts, M., Mozer, M. C., Cho, K., & Bengio, Y. (2021). RL-Square: Decoupling strategy and reward for generalization in reinforcement learning. In International Conference on Learning Representations.
[18]. Frank, M., Leitner, D., Zambanini, S., & Vincze, M. (2014). Curiosity-driven exploration for knowledge discovery. Autonomous Robots, 37(1), 87-104.
[19]. Eysenbach, B., Gupta, A., Ibarz, J., & Levine, S. (2018). Diversity is all you need: Learning skills without a reward function. In International Conference on Learning Representations.
[20]. Andrychowicz, M., Wolski, F., Ray, A., Schneider, J., Fong, R., Welinder, P., McGrew, B., Tobin, J., Abbeel, P., & Zaremba, W. (2017). Hindsight experience replay. In Advances in Neural Information Processing Systems (pp. 5048-5058).
[21]. Aubret, A., Matignon, L., & Hassas, S. (2019). A survey on intrinsic motivation in reinforcement learning. arXiv preprint arXiv:1908.06976.
[22]. Schmidhuber, J. (2010). Formal theory of creativity, fun, and intrinsic motivation (1990-2010). IEEE Transactions on Autonomous Mental Development, 2(3), 230-247.
[23]. Brockman, G., Cheung, V., Pettersson, L., Schneider, J., Schulman, J., Tang, J., & Zaremba, W. (2016). OpenAI gym. arXiv preprint arXiv:1606.01540.
[24]. Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-time analysis of the multi-armed bandit problem. Machine Learning, 47(2), 235-256.
[25]. Agrawal, S., & Goyal, N. (2012). Analysis of Thompson sampling for the multi-armed bandit problem. In Conference on Learning Theory (pp. 39-1). PMLR.
[26]. Van Hasselt, H., Guez, A., & Silver, D. (2016). Deep reinforcement learning with double Q-learning. Proceedings of the AAAI Conference on Artificial Intelligence, 30(1).
[27]. Schaul, T., Quan, J., Antonoglou, I., & Silver, D. (2015). Prioritized experience replay. In International Conference on Learning Representations.
[28]. Wang, Z., Schaul, T., Hessel, M., Van Hasselt, H., Lanctot, M., & De Freitas, N. (2016). Dueling network architectures for deep reinforcement learning. In International Conference on Machine Learning (pp. 1995-2003). PMLR.
Cite this article
Cao,Z.;Jiang,J.;Liu,H. (2024). Curiosity-Driven Multi-Level Intrinsic Reward DQN for Enhanced Exploration in Reinforcement Learning. Applied and Computational Engineering,103,142-151.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 2nd International Conference on Machine Learning and Automation
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An introduction. MIT Press.
[2]. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., Graves, A., Riedmiller, M., Fidjeland, A. K., & Ostrovski, G. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529-533.
[3]. Kaelbling, L. P., Littman, M. L., & Moore, A. W. (1996). Reinforcement learning: A survey. Journal of Artificial Intelligence Research, 4, 237-285.
[4]. Osband, I., Blundell, C., Pritzel, A., & Van Roy, B. (2016). Deep exploration via bootstrapped DQN. In Advances in Neural Information Processing Systems (pp. 4026-4034).
[5]. Bellemare, M. G., Srinivasan, S., Ostrovski, G., Schaul, T., Saxton, D., & Munos, R. (2016). Unifying count-based exploration and intrinsic motivation. In Advances in Neural Information Processing Systems (pp. 1471-1479).
[6]. Oudeyer, P. Y., Kaplan, F., & Hafner, V. V. (2007). Intrinsic motivation systems for autonomous mental development. IEEE Transactions on Evolutionary Computation.
[7]. Schmidhuber, J. (1991). A possibility for implementing curiosity and boredom in model-building neural controllers. In Proceedings of the International Conference on Simulation of Adaptive Behavior: From Animals to Animats (pp. 222-227).
[8]. Berlyne, D. E. (1960). Conflict, arousal, and curiosity. McGraw-Hill Book Company.
[9]. Gopnik, A., Meltzoff, A. N., & Kuhl, P. K. (1999). The scientist in the crib: What early learning tells us about the mind. William Morrow & Co.
[10]. Pathak, D., Agrawal, P., Efros, A. A., & Darrell, T. (2017). Curiosity-driven exploration by self-supervised prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (pp. 16-17).
[11]. Burda, Y., Edwards, H., Pathak, D., Storkey, A., Darrell, T., & Efros, A. A. (2018). Exploration by random network distillation. In International Conference on Learning Representations.
[12]. Houthooft, R., Chen, X., Isola, P., Stadie, B. C., Wolski, F., Ho, J., & Abbeel, P. (2016). VIME: Variational information maximizing exploration. In Advances in Neural Information Processing Systems (pp. 1109-1117).
[13]. Singh, S., Barto, A. G., & Chentanez, N. (2004). Intrinsically motivated reinforcement learning. In Advances in Neural Information Processing Systems (pp. 1281-1288).
[14]. Stadie, B. C., Levine, S., & Abbeel, P. (2015). Incentivizing exploration in reinforcement learning with deep predictive models. In International Conference on Learning Representations.
[15]. Burda, Y., Edwards, H., Pathak, D., Storkey, A., Darrell, T., & Efros, A. A. (2018). Large-scale study of curiosity-driven learning. In International Conference on Learning Representations.
[16]. Achiam, J., Edwards, H., Amodei, D., & Abbeel, P. (2017). Surprise-based intrinsic motivation for deep reinforcement learning. In Advances in Neural Information Processing Systems.
[17]. Stanton, C., Tachet des Combes, R., Wang, G., Roberts, M., Mozer, M. C., Cho, K., & Bengio, Y. (2021). RL-Square: Decoupling strategy and reward for generalization in reinforcement learning. In International Conference on Learning Representations.
[18]. Frank, M., Leitner, D., Zambanini, S., & Vincze, M. (2014). Curiosity-driven exploration for knowledge discovery. Autonomous Robots, 37(1), 87-104.
[19]. Eysenbach, B., Gupta, A., Ibarz, J., & Levine, S. (2018). Diversity is all you need: Learning skills without a reward function. In International Conference on Learning Representations.
[20]. Andrychowicz, M., Wolski, F., Ray, A., Schneider, J., Fong, R., Welinder, P., McGrew, B., Tobin, J., Abbeel, P., & Zaremba, W. (2017). Hindsight experience replay. In Advances in Neural Information Processing Systems (pp. 5048-5058).
[21]. Aubret, A., Matignon, L., & Hassas, S. (2019). A survey on intrinsic motivation in reinforcement learning. arXiv preprint arXiv:1908.06976.
[22]. Schmidhuber, J. (2010). Formal theory of creativity, fun, and intrinsic motivation (1990-2010). IEEE Transactions on Autonomous Mental Development, 2(3), 230-247.
[23]. Brockman, G., Cheung, V., Pettersson, L., Schneider, J., Schulman, J., Tang, J., & Zaremba, W. (2016). OpenAI gym. arXiv preprint arXiv:1606.01540.
[24]. Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-time analysis of the multi-armed bandit problem. Machine Learning, 47(2), 235-256.
[25]. Agrawal, S., & Goyal, N. (2012). Analysis of Thompson sampling for the multi-armed bandit problem. In Conference on Learning Theory (pp. 39-1). PMLR.
[26]. Van Hasselt, H., Guez, A., & Silver, D. (2016). Deep reinforcement learning with double Q-learning. Proceedings of the AAAI Conference on Artificial Intelligence, 30(1).
[27]. Schaul, T., Quan, J., Antonoglou, I., & Silver, D. (2015). Prioritized experience replay. In International Conference on Learning Representations.
[28]. Wang, Z., Schaul, T., Hessel, M., Van Hasselt, H., Lanctot, M., & De Freitas, N. (2016). Dueling network architectures for deep reinforcement learning. In International Conference on Machine Learning (pp. 1995-2003). PMLR.