1. Introduction

Pathfinding algorithms play a crucial role in the process of route planning and navigation for objects, and have been involved in autonomous driving systems, robot navigation systems and games. In this paper, the example of the pathfinding system in games will be taken to find the optimal pathfinding algorithm to find the shortest path while minimizing the time consumed.

In order to realize efficient path finding, there have been many researches on pathfinding algorithms. Dijkstra's algorithm, which was first published in 1959, is a traditional pathfinding algorithm, which starts from the starting point and searches for the nearest unsearched accessible phases to the starting point, until the end point is searched. The algorithm has been applied in the present, and in 2014 Chen et al. constructed a vehicle evacuation optimal route model using Dijkstra's algorithm [1]. The algorithm has also been optimized many times nowadays. In 2012 Shu-Xi improved some of the defects of the algorithm, optimized the exit mechanism, and improved the operation efficiency [2].

Another algorithm to get higher running speed, starting from the starting point and selecting only the node with the shortest predicted distance to the end point each time until it reaches the end point is the Best First Search algorithm. Although the running speed is extremely fast, due to the poor accuracy of its prediction function, it is almost impossible to get the shortest path in complex environments.

A Star algorithm is a path finding algorithm that combines the advantages of the two algorithms. It starts from the starting point, searches and selects neighboring nodes with the smallest cost until the end point is found. The cost of each node consists of the sum of two parts, one part is the actual distance cost based on Dijkstra's algorithm, and the other part is the predicted distance cost based on the Best First Search algorithm. A Star algorithm is extremely widely used in reality. In the field of robot navigation system, Duchoň et al. designed a path planning system for mobile robot based on A Star algorithm in 2014, and Ma designed a robot path planning and obstacle avoidance system based on A Star algorithm in 2024, and in the same year, Zhang et al. introduced global obstacle information and local obstacle information and U-shaped "trap" region to optimize the robot A Star algorithm [3-5]. In the field of vehicle navigation system, Yin et al. proposed a vehicle navigation system completely based on A Star algorithm in 2013, and Erke et al. optimized the A Star algorithm and designed an autonomous land vehicles navigation system based on A Star algorithm in 2020 [6, 7]. In the field of vessel path planning, in 2019 Liu et al. improved the A Star algorithm for vessel path planning [8].

And in game design, a game object needs to consider various obstacles and find the shortest path from the starting point to the end point, which also requires path finding algorithms. In 2018 Permana et al. compared multiple paths finding algorithms in game design and concludes that the A Star path finding algorithm is the most appropriate path finding algorithm [9]. In 2022 Lawande et al. also used the Unity Game Engine to test different path finding algorithms and in the conclusion A Star algorithm is lower than the Best First Search algorithm in terms of running speed but has a better ability to cope with obstacles [10].

The A Star algorithm is not completely without flaws, due to the combination of Dijkstra's algorithm and the Best First Search algorithm in the A Star algorithm, the A Star algorithm is neither the fastest algorithm, nor is it guaranteed to find the shortest distance. However, for the game route planning, both have the same important status, and A Star algorithm can take both into account, compared with other algorithms is undoubtedly more suitable. Therefore, this paper will be based on the Godot game engine, using C Sharp language to design an A Star routing system in the game route planning and research how to optimize the system.

2. Methodology

2.1. Data source

Using the Godot game engine, a test program written in C Sharp can generate a map of a certain size and randomly generate obstacles and a starting point and find the path to other points and record the length of the path, using the mouse to set the end point and display its path and using buttons to switch between different path forms and pathfinding prediction functions.

The program can obtain the route data from the starting point to different points, and obtain multiple sets of data by changing the different pathfinding estimation functions (Euclidean distance and Manhattan distance). In this paper, a 5x5 size waypoint was selected in the upper left corner of the entire map for path length data collection. At the same time, this paper also collects path images using different path forms and pathfinding functions.

2.2. Test standard

According to the actual path design requirements, the response ability of different path forms to obstacles and the path length are compared, and the most suitable path form is found.

The path lengths of the two estimation function algorithms, Euclidean distance and Manhattan distance, are compared and analyzed, and the optimal estimation function algorithm is found.

2.3. Method introduction

The whole pathfinding system uses the A Star algorithm as the core algorithm, and the A Star algorithm is an excellent pathfinding algorithm, which mainly includes the following steps:

Step 1 is to split the whole map into multiple nodes.

Step 2 is to start from the starting point by adding the passable nodes around the starting point, ignoring obstacles, adding to the open list, and setting the starting point to their parent.

Step 3 is to add the starting point to the close list.

Step 4 is to calculate the cost F of all nodes, and the cost calculation formula is shown in the following equation (1)

\( F=G+H \) (1)

where G is the actual path movement cost function, in order to detect the length of the path passed, G of each node is the G value of its parent node plus the distance from its parent node to the node, and H is the estimated function from the node to the end point.

Step 5 is to find the node with the least cost in the open list, as a new starting point, and look for the nodes in proper order that can pass around it, ignoring the obstacles and the nodes in the close list. If it is not in the open list, it should be put into the open list and set its parent as the node. If it is already in the open list, its new cost and the original cost size should be compared, and if it is smaller than the original, its cost should be changed to the new price, and its parent node should be changed to the new starting node, otherwise, no action is taken.

Step 6 is to repeat steps 3 to 5 until the end is added to the start list.

Step 7 is to start from the end point and keep looking for the parent until finding the starting point to get the path.

The estimation function H uses the Euclidean distance and the Manhattan distance. The Euclidean distance is calculated as shown in equation (2), and the Manhattan distance is calculated as shown in equation (3).

\( H={(\left({X_1 - X}_2\right)^2+\left({Y_1 - Y}_2\right)^2)}^\frac{1}{2} \) (2)

\( H=\left|{X_1 - X}_2\right|+\left|{Y_1 - Y}_2\right| \) (3)

The Euclidean distance is the shortest distance that allows movement in all directions and is more complex to calculate, while the Manhattan distance is the shortest distance that only allows movement in the horizontal and vertical directions, and is simpler to calculate.

In addition, the algorithm is improved to meet the actual design requirements by detecting the surrounding obstacles and setting markers for the impassable diagonal nodes before steps 2 and 5, and not adding them to the on list in steps 2 and 5.

3. Results and discussion

3.1. Pathfinding algorithm improvement

First completed the preparation of the basic program, the program can complete the basic functions required above and its software interface is shown in figure 1 below. The black part is the obstacle and the dot is the moving object. The upper number displays the acquired path length.

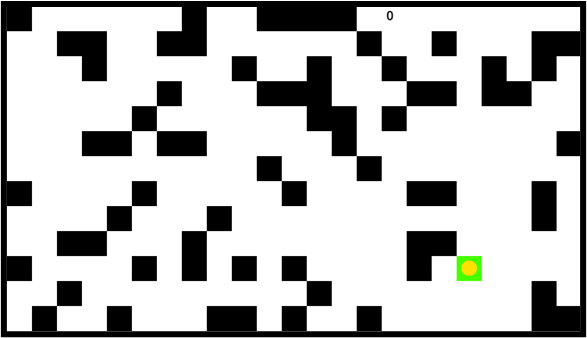
Figure 1. Software Basic Interface

When the mouse clicks on any non-obstacle part, a path is generated according to the algorithm, as shown in figure 2 below, with the green part as the path.

Figure 2. First generation of roadmap

In the basic design of the pathfinding algorithm, the basic principle of A Star algorithm was firstly adopted for the program design, and Godot game engine and C Sharp were used to complete the writing of the whole test software, which can randomly generate obstacles and generate a moving object, and through the pathfinding algorithm. The distance from the object to the mouse click position was calculated and the specific path was displayed on the screen. However, the path found by the most basic pathfinding algorithm is not the required path, and the path should not be able to cross the diagonal in the middle when there are obstacles above and to the left or above and to the right or below and to the left or below and to the right of the moving object at the same time, but the basic A Star algorithm cannot realize the requirement and needs to be improved.

Therefore, in order to solve the problem, a simple improvement was firstly proposed. It is disallowing diagonal movement of paths and detecting only the four directions of top, bottom, left and right in path detection, which can completely circumvent the problem of diagonal crossing of obstacles as shown in figure 3 below, but this time it makes the length of the paths significantly longer, which is contrary to the need of finding shorter paths.

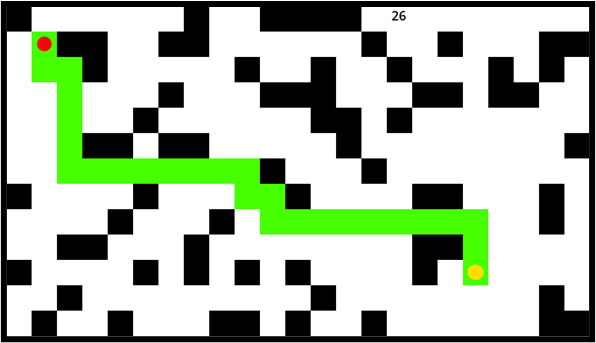
Figure 3. Roadmap obtained by prohibiting diagonal movement

There exists a more effective improvement method that does not include diagonal nodes caught by obstacles when searching for open nodes, and after improving the method, the program can find a path while avoiding the problem of crossing obstacles diagonally as shown in figure 4 below. Compared with the previous improved method, the steps are more complicated and the performance consumption is higher, but a shorter path can be found, and this paper finally concludes that this improved method is superior and has value for use.

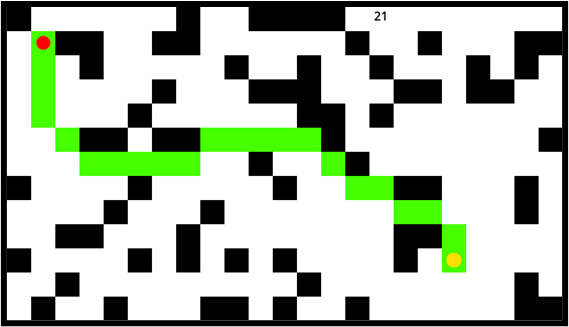
Figure 4. Roadmap with improved algorithm

3.2. Estimated function selection

In this paper, based on the improved A Star algorithm mentioned above, the two estimated functions were tested separately, so that the software outputs all the path lengths within the 5x5 region in the upper left corner. First, the path lengths using the Euclidean distance were tested as shown in table 1 below, where -1 means this node is an obstacle or there is no path, and obstacle density is one obstacle per 24 nodes.

Table 1. Table of path lengths obtained from Euclidean distances.

After that, the path lengths using Manhattan distance were tested as shown in table 2.

Table 2. Table of path lengths obtained from Manhattan distances.

After comparing the two sets of data, it is found that both have the same path lengths obtained for some of the coordinates. In coordinates where some of the paths have different lengths, Manhattan distance is a little shorter in \( \left(x_1,y_3\right) \) and \( \left(x_2,y_4\right) \) , while Euclidean distance is much shorter in \( \left(x_1,y_2\right) \) , \( \left(x_2,y_1\right) \) , \( \left(x_2,y_2\right) \) , \( \left(x_3,y_1\right) \) , \( \left(x_4,y_1\right) \) , \( \left(x_5,y_1\right) \) and \( \left(x_5,y_2\right) \) .

The result has shown that Euclidean distance can get much shorter path in more coordinates and it seems to be much better than Manhattan distance. Since the estimated function is only a prediction, the final cost synthesized is not accurate, and when comparing the cost-size relationship, the path found may not be the shortest due to this error. According to the results of software testing, the Euclidean distance is better than the Manhattan distance to avoid this problem, and the Euclidean distance should be chosen as the optimized function when performance allows.

4. Conclusion

In this paper, after completing the writing of the routing system program using C Sharp and Godot game engine, the routing algorithm as well as the whole routing program were analysed and optimized according to the routing results. After discovering the defects of A Star algorithm in the actual program design, the algorithm was improved to prevent the occurrence of the error that the route crosses the obstacles through the diagonal by detecting the obstacles. In addition, comparing different estimated functions, and through the path length data output by the program, it was found that the Euclidean distance was more suitable as the estimated function than the Manhattan distance, and the Euclidean distance was finally adopted as the estimated function in this pathfinding system. After completing the above series of improvements, the design and writing of the whole pathfinding system program is completed, which can realize randomly generating obstacles and generating a moving object, and find the path from the object to the mouse click position and display the path on the screen. The program utilizes the improved A Star algorithm, which is of practical significance for the pathfinding system in the game. When this system is applied to game design in the future, its pathfinding algorithm is still optimized for improvement in the face of more complex environments, including the optimization of pathfinding speed and the optimization of the ability to cope with complex terrain.