1. Introduction

Machine learning has achieved rapid development from theory to practical application over the past few decades and has become a core driver of artificial intelligence and data analytics. Machine learning techniques are widely used in areas ranging from image recognition and speech recognition to personalized recommendation systems [1, 2]. With the explosive growth of data volume and increasing computational demands, traditional stand-alone machine learning approaches face performance bottlenecks in processing large-scale data. Therefore, distributed machine learning becomes a necessary approach that improves efficiency and processing power by distributing computational tasks across multiple compute nodes [3, 4]. Distributed learning appears to be critical for providing solutions for learning from ‘mega’ datasets (large-scale learning) and naturally distributed datasets. The number of learning sites can be increased to offset growth in data volume, resulting in a scalable learning solution. In addition, distributed learning saves time and money by not having to collect data at a single workstation for centralized processing. Although there are obvious advantages to distributed learning, new challenges arise, such as the impact of inter-subdivision data heterogeneity on accuracy or the need to protect inter-subdivision data's privacy [5].

Distributed machine learning can be used in a variety of industries, especially in finance, healthcare, information and communication, and the accelerating manufacturing industry [6-8]. With the exponential growth of data size, traditional stand-alone learning models are difficult to handle such huge amounts of data. By distributing data and computational tasks across multiple nodes, distributed machine learning can effectively tackle the challenges of big data processing [9]. Increasing global investment and research in machine learning has fueled the rapid development of new technologies. Future research hotspots in machine learning include advances in techniques such as deep learning, reinforcement learning, and automatic machine learning (AutoML) [10]. How to improve model interpretability, privacy protection and model fairness are also key challenges for machine learning in the future. With the popularity of machine learning technology, different countries have adopted different regulatory strategies for its development, especially needing to pay attention to laws and regulations on privacy protection and data security. Joint learning, as an emerging technique to protect data privacy, allows multiple participants to train models together without sharing raw data. In the future, joint learning will become an important direction for distributed machine learning, especially in the areas of privacy protection and data security [11, 12]. With the popularity of Internet of Things (IoT) devices, the combination of edge computing and distributed machine learning has become a new research hotspot. In edge computing, data processing and analyses are performed in close proximity to the data source, which can reduce latency and improve response time [13].

This study hopes to explore how to select the optimal distributed machine learning model according to the characteristics of the dataset, focusing on the performance differences between different distributed machine learning models under the same dataset in terms of convergence speed, accuracy, etc., and their reasons, and the selected models are XGboost decision tree and deep neural network. The following pages will give a thorough explanation of these two models and the chosen database, as well as the performance variances between the two types of models under the chosen databases and the explanations for these variations. Finally, this study would like to share some research insights and limitations of this paper, and provide an outlook for future research.

2. Data and method

XGBoost is an optimization algorithm based on the Gradient Boosting framework. XGBoost's main objective is to create a powerful predictive model by combining multiple weak learners (typically decision trees). By learning from the previous model's error, each new model gradually reduces the overall error and improves prediction accuracy. The XGBoost algorithm can be understood in the following ways. The objective function is defined as:

\( Obj(\theta)=\sum_{i=1}^{n}{L(\gamma_i,{\hat{\gamma}}_i)+}\sum_{k=1}^{K}{\omega(f_k)} \) (1)

The regularization term usually penalizes the number of leaf nodes \( T \) and leaf node weights w of the tree in the following form:

\( \omega(f)=\gamma T+\frac{1}{2}\lambda\sum_{j=1}^{T}w_j^2 \) (2)

XGBoost uses an iterative approach to add new weak learners. Assuming that the prediction value of the current model is \( \ {\hat{\gamma}}_i^{(t)} \) , in the first \( t+1 \) iteration, XGBoost will construct a new tree \( f_{t+1}\ \) to learn the residuals of the previous model. The new predicted values are:

\( {\hat{\gamma}}_i^{(t+1)} \) = \( \ {\hat{\gamma}}_i^{(t)} \) + \( f_{t+1}(x_i) \) (3)

To minimise the objective function, XGBoost uses a second-order Taylor expansion to approximate the loss function. This causes the objective function to become at each iteration:

\( {Obj}^{(t+1)}\approx\sum_{i=1}^{n}\left[g_if_{t+1}\left(x_i\right)+\frac{1}{2}h_if_{t+1}^2\left(x_i\right)\right] \) + \( \omega(f_{t+1}) \) (4)

where \( g \) and \( h \) are the gradient and second order derivative (i.e., Hessian) of the loss function, respectively, denoted as:

\( g_i=\frac{\partial L(y_i,{\hat{y}}_i^{\left(t\right)})}{\partial{\hat{y}}_i^{(t)}} \) , \( h_i=\frac{\partial^2L(y_i,{\hat{y}}_i^{\left(t\right)})}{\partial{({\hat{y}}_i^{\left(t\right)})}^2} \) (5)

In order to find the best tree structure in each iteration, XGBoost uses a greedy algorithm for node splitting. Specifically, it calculates the gain of the objective function by enumerating all possible splitting points, and the best splitting point for the current node is chosen based on the highest gain. For each candidate split point, the gain is calculated as:

\( Gain=\frac{1}{2}\left[\frac{{(G_L+G_R)}^2}{H_L+H_R+\lambda}−\frac{G_L^2}{H_L+\lambda}−\frac{G_R^2}{H_R+\lambda}\right]−\gamma \) (6)

where \( G_L \) and \( G_R \) are the sum of the gradients of the left and right subtrees, and \( H_L\ \) and \( H_R \) are the sum of the second order derivatives of the left and right subtrees. To prevent the model from overfitting, XGBoost performs pruning after constructing the tree. By calculating the objective function after pruning, XGBoost determines whether to remove some unimportant branches, thus simplifying the model. Fig. 1 gives the sketch for the model.

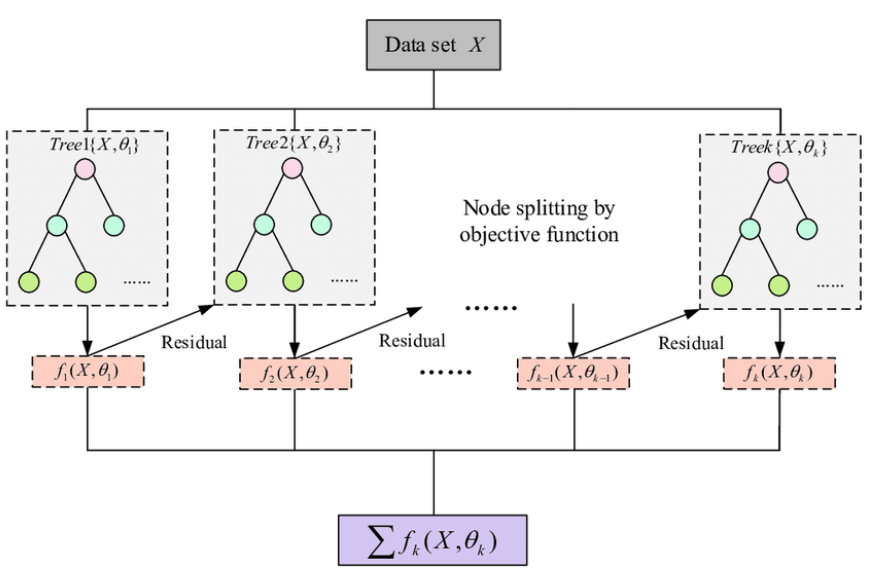
Figure 1. A sketch of XGBoost (Photo/Picture credit: Original).

Deep Neural Network (DNN) is an artificial neural network that has various hidden layers. By simulating the structure of biological neural networks, DNN is capable of handling complex non-linear relationships. The DNN is made up of multiple layers of neurons, all of which are connected to the neurons in the previous layer. In a typical DNN, there is an input layer, multiple hidden layers, and an output layer. The input layer receives input data, the hidden layers extract features, and the output layer generates the final prediction. Each neuron in DNN is given a weighted sum of the outputs from the previous layer and produces an output using an activation function. The output for the j, which is the neuron of a specific layer, is as follows:

\( a_j^{(l)}=\sigma(\sum_{i=1}^{n}\omega_{ij}^{\left(l\right)}a_i^{\left(l−1\right)}+b_j^{\left(l\right)}) \) (7)

An activation function is designed to introduce nonlinearity to enable the network to fit complex functional relationships. Commonly used activation functions include:

ReLU (Rectified Linear Unit): \( \sigma\left(x\right)=max(0,x) \)

Sigmoid: \( \sigma\left(x\right)=\frac{1}{1+e^{−x}} \)

Tanh: \( \sigma\left(x\right)=tan{h(x)} \)

DNN calculates the output of each layer by forward propagation and finally generates the prediction at the output layer. For the whole network, the forward propagation can be expressed as:

\( \hat{y}=f(x;\theta) \) (8)

where \( f\left(x;\theta\right)\ \) is the output function of the neural network and \( \theta\ \) is the set of parameters of the network, including all weights and biases. The loss function is used to measure the difference between the predicted value \( \hat{y}\ \) and the true value \( \ y \) . Common loss functions are Mean Square Error (MSE) used in regression tasks:

\( L\left(y,\hat{y}\right)=\frac{1}{n}\sum_{i=1}^{n}{(y_i−{\hat{y}}_i)}^2 \) (9)

and Cross-Entropy Loss for classification tasks:

\( L\left(y,\hat{y}\right)=−\sum_{i=1}^{n}{y_ilog{({\hat{y}}_i)}} \) (10)

DNN optimizes the network parameters by means of a backpropagation algorithm. Backpropagation calculates the gradient of the loss function with respect to each parameter and updates the parameters by a gradient descent algorithm to minimize the loss function. The gradient of each parameter is computed by the chain rule:

\( \frac{\partial L}{\partial\omega_{ij}^{(l)}}=\frac{\partial L}{\partial a_j^{(l)}}\bullet\frac{\partial a_j^{(l)}}{\partial z_j^{(l)}}\bullet\frac{\partial z_j^{(l)}}{\partial w_{ij}^{(l)}} \) (11)

The one needs to update weights and bias using gradient descent.

\( w_{ij}^{(l)}\gets w_{ij}^{(l)}−\eta\bullet\frac{\partial L}{\partial\omega_{ij}^{(l)}} \) (12)

where η is the learning rate, which controls the step size of each update. Deep neural networks are able to efficiently model complex nonlinear relationships through the combination of multiple layers of neurons and nonlinear activation functions. Its core algorithms include forward propagation, backpropagation and gradient descent.

The dataset comes from a Chinese telecom company. Using the user attributes that already exist (such as basic personal information, user profile information). The user's phone brand, business attributes, consumption habits, and preferences are used to match them with the most suitable cellular plan and provide personalized services. The descriptions for the data are as following:

• Sample size: 320k

• Train size: 300k (150k each)

• Validation size: 20k

• Categories: 9

• Dimension: 25 Groups

This research splits the 300k training set into 2 sets in 3 different configurations. For 9 encoded categories: 1, 3, 5, 7 as Group A; 0, 2, 4, 6, 8 as Group B. 2 sets with distinct labels (one with all Group A, the other with all Group B). 2 sets with all labels but imbalanced proportions (one with 85% Group A, 15% Group B; the other with 15% Group A, 85% Group B; Label Distribution Skew). For homogeneous (Little Heterogeneity), this study randomly shuffled and split into two. For metrics, accuracy and MSE (Mean Squared Error) are adopted.

3. Results and discussion

3.1. Model performance

The results of the XGBoost experiment were beyond the expectations, and the original intention was to make some speculations and explorations on the mathematical principles of the two problems by comparing the differences in the experimental results. However, the XGBoost model is too good in the performance of telecom package matching, in the experiment, it does not even need to iterate at all, after the first round of initialization is completed, it will reach an AUC value of about 97.7, and in the process of iteration it continues to decline (presumably overfitting), but the decline is not more than 1, and the overall iteration of 100 rounds still maintains an AUC value of about 96, and the data difference is too small to analyze. For DNN, with 10 global iterations, this study used τ1 and τ2 and different heterogeneity levels to train models (seen the configuration in Table 1). All Trained Models are shown in Fig. 2 and Fig. 3.

Table 1. Configurations used to train the models

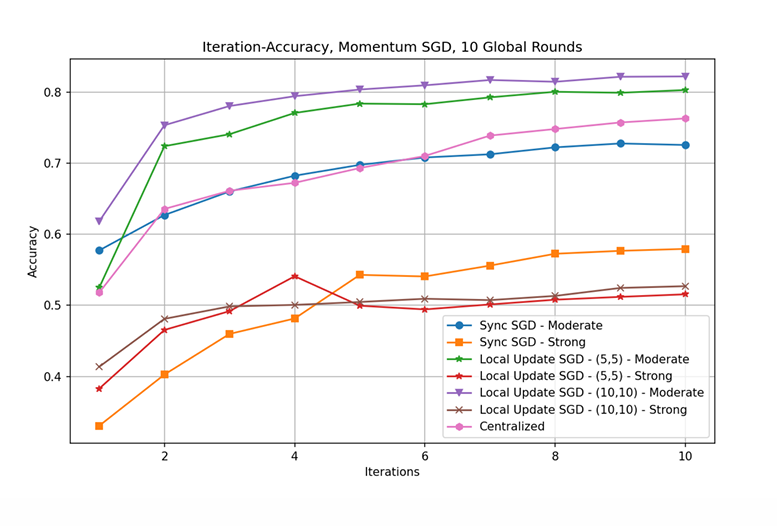
Figure 2. Iterations-Accuracy Plot (Photo/Picture credit: Original).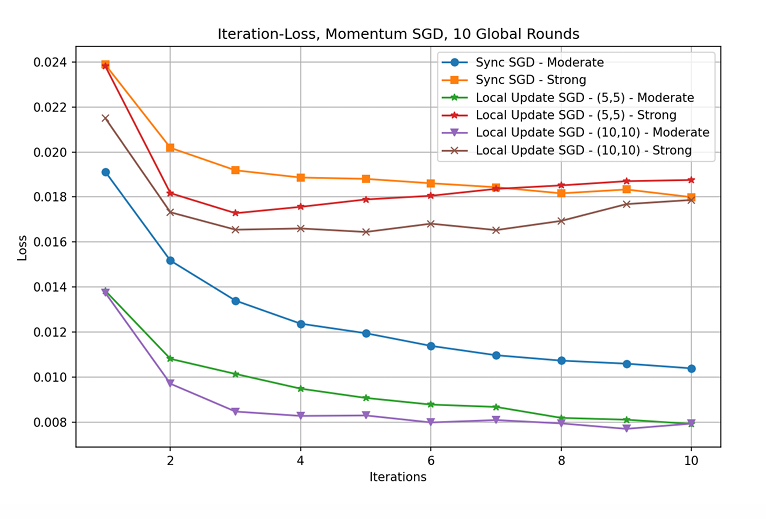

Figure 3. Iterations-Loss Plot (Photo/Picture credit: Original).

3.2. Comparison and explanation

Strong heterogeneity leads to poor error floor (upper group of lines has strong heterogeneity (Non-IID)). In this case, larger τ instead have lower error floor across the board. This might be due to the dataset not meeting the requirements for Lipschitz smoothness, so the conclusion ” Larger τ gives worse error convergence” may not hold in this particular case. This study used another setting with the same level of data heterogeneity but different device heterogeneity setting.

Meanwhile, it is thought the reason for the difference in accuracy between the two models is that the models are applicable to different datasets, XGboost is applicable to small and medium-sized unbalanced discrete datasets, and at the same time performs better on structured data with some missing data, while DNN is applicable to large-scale, high-dimensional datasets with complex non-linear relationships, especially in the fields of image, speech, natural language processing and time series, etc. Excellent performance. At the same time DNN requires a large amount of data and computational resources. This dataset selected is a small to medium sized dataset, while only 25 dimensions, such dataset size is not enough for DNN to have sufficient training (seen from Table 2).

Table 2. Device Heterogeneity

3.3. Limitations and prospects

In the experiments, two models, XGBoost and DNN, were used to process 25-dimensional telecom company subscriber data. Despite the advantages of each of these two models, the experiment still has some limitations. Only two models, XGBoost and DNN, were selected for the experiment, which limits the breadth of the results. Other models (e.g. Support Vector Machines, Random Forests, Logistic Regression, K Nearest Neighbors) may perform better or be more explanatory on this dataset. Besides, no comparisons were made using simple baseline models (e.g., logistic regression or linear regression) to effectively assess the relative strengths of DNN and XGBoost on this particular dataset. Meanwhile, the relatively low dimensionality of the telecom company subscriber data with 25-dimensional features may not fully utilize the strengths of DNN.DNN is more effective in dealing with high-dimensional and complex data, and therefore DNN may not perform significantly better than traditional machine learning models on this lower dimensional dataset. If the dataset has a small number of samples, DNN may perform poorly due to overfitting. DNN usually requires large-scale data to be adequately trained, whereas XGBoost may be more robust with fewer samples. In fact, DNN is a black box model and it is difficult to explain its decision-making process. Although XGBoost provides feature importance analyses, the lack of further model interpretation may limit the comprehensibility of experimental results, especially for business decision-making processes. Business scenarios of telecommunication companies may require a clear explanation of the model decision-making process in order to make appropriate business decisions. Lack of interpretability may lead to limitations in the application of the model. In addition, this study failure to adequately tune the hyperparameters of DNN and XGBoost may affect the performance of the models. In particular, the structure and hyperparameters of DNN (number of layers, number of neurons, activation function, etc.) have a greater impact on the performance, and the tuning of these aspects may require more time and computational resources. The experimental data is only from telecommunication company users and may not be generalizable to other domains. If the goal is to develop a generalized model, datasets from different domains need to be tested.

4. Conclusion

To sum up, this study presents a comparative analysis of XGBoost and Deep Neural Networks (DNN) using a telecom customer dataset containing 320,000 samples and 25 features. XGBoost performs well, quickly achieving a high AUC of 97.7% with a minimal number of iterations, which suggests its suitability for small to medium-sized, structured and unbalanced datasets. In contrast, DNN was tested under conditions with varying degrees of data heterogeneity, with larger errors in the more heterogeneous environments, possibly due to non-smoothing issues. While DNN is very powerful in large, high-dimensional and complex data (e.g., image or speech processing), its performance on low-dimensional datasets is less robust. The study also highlights its limitations, including limited model diversity (only XGBoost and DNN were used) and the low dimensionality of the dataset, which may not take full advantage of DNN. In addition, the paper identifies challenges in model interpretability (especially for DNNs) and suggests that future research could benefit from incorporating more diverse models, optimizing hyperparameters, and focusing on improving model transparency for better commercial applications.