Keyword: Federated learning; deep learning, pruning, quantization, knowledge distillation.

1. Introduction

In recent years, the volume of data has increased tremendously due to the rapid development and popularization of Internet of Things (IoT) devices, sensors, and smart terminals. Although these massive data provide solid data support for the construction of various artificial intelligence models, it is very difficult to centrally process these data with different structures, which poses challenges to data privacy and security [1]. Federated learning, a distributed machine learning paradigm that addresses these problems, enables several users to work together to train a global model without sharing data, guaranteeing security and anonymity while utilizing distributed data resources [2].

Academics and industry alike are paying more and more attention to federated learning, which has made great strides in a number of applications. The design of distributed optimization algorithms works as the cornerstone of federated learning. Federated Averaging (FedAvg) weight averages the parameter gradient of selected local clients to update the center server. To alleviate the problem of data heterogeneity (non-iid data distribution) in FedAvg, Federated Proximal (FedProx) further introduces a regularization term in the standard FedAvg to control the update of the client's local model, making it closer to the global model, thereby improving the training effect of the model in the case of uneven data distribution. Though these efforts have advanced the performer of federated learning, the large communication volumes remain an open issue, leading to low training efficiency, especially given the limited computing and communication capabilities of many devices. Motivated by the swift advancement of lightweight models, scholars have suggested utilizing knowledge distillation, quantization, and pruning techniques to enhance the effectiveness of federated learning. These methods aim to reduce the model's complexity and communication volume, thus enhancing the overall efficiency of federated learning. Specifically, pruning reduces the model size by eliminating insignificant neural network connections; quantization reduces computational and storage costs by lowering the precision of model parameters; and knowledge distillation compresses the model by transferring the knowledge from a larger model to a smaller one [3-5].

In this paper, we are committed to exploring the role of representative lightweight technologies in promoting the learning efficiency of federated learning models, which can provide a decision-making basis for method selection in practical applications. Specifically, we not only embed pruning, quantization, and knowledge distillation modules separately in the classic reinforcement learning network but also combine the above compression technologies in the unified model. By quantitatively comparing the accuracy, loss value, delay, and transmission ratio of different models, we determine the best combination to balance the model performance and learning efficiency. Our cascaded lightweight technique has been shown through extensive trials to be effective in reducing the training overhead of federated learning. To summarize, our main contribution includes:

(1) The optimization effect of different lightweight technologies is quantitatively studied on the learning efficiency of federated learning models, providing a decision-making basis for algorithm selection in large-scale practical applications.

(2) The interaction effect of different lightweight technologies are further explored, where pruning, quantization and knowledge distillation can complement each other to achieve the best balance between model accuracy and speed.

(3) A number of tests are conducted to confirm that our combined lightweight strategy works.

2. Related Work

2.1. Pruning

Pruning, which can be divided into weight pruning and structured pruning, is a model compression approach that includes cutting out unnecessary neural network connections to minimize the size and computing burden of the model. He et al. [5] proposed a convolutional neural network (CNN) compression method that combines pruning with knowledge distillation. This approach effectively reduces parameters and computations while maintaining model performance. The combination of pruning with other techniques, such as knowledge distillation, has been shown to enhance the overall efficiency of model compression [6].

2.2. Quantization

Quantization reduces computational and storage costs by lowering the precision of model parameters. Polino et al. [4] demonstrated that combining quantization with knowledge distillation allows for significant model compression without substantial performance loss. This method reduces the model's complexity and communication volume, thereby improving the overall efficiency of federated learning. Liu et al. [7] further explored the synergy of quantization and knowledge distillation, highlighting its potential to enhance controllability and efficiency in the compression process.

2.3. Knowledge Distillation

Knowledge distillation entails moving knowledge from a larger model to a smaller one in order to achieve compression. Li et al. [3] introduced the PQK method, which combines pruning, quantization, and knowledge distillation to enhance compression efficiency. Cheng et al. [8] conducted a detailed analysis of knowledge distillation's application in model compression, discussing the impact of different hyperparameter settings and model architectures on the compression effect.

2.4. Combined Compression Techniques

The limitations of single compression methods have driven researchers to explore combinations of these techniques for better results. For instance, combining pruning and knowledge distillation significantly reduces model size and improves efficiency [9-10]. Similarly, previous work has shown the potential of integrating quantization with knowledge distillation to enhance compression efficiency without compromising performance [11-12]. The integrated application of pruning, quantization, and knowledge distillation, as demonstrated by Zhang et al. [13], significantly improves model compression efficiency, particularly in IoT applications. The comprehensive analysis of recent literature [14-15] underscores the critical role of model compression in enhancing the efficiency of federated learning. Single compression techniques often fall short in balancing compression efficiency and model performance. Therefore, combined methods have emerged as a more robust approach. By integrating multiple techniques, it is possible to leverage their complementary strengths, resulting in models that are both compact and high-performing. This study aims to systematically compare these methods to identify the optimal combination, providing valuable insights for the application of federated learning in IoT data processing.

3. Method

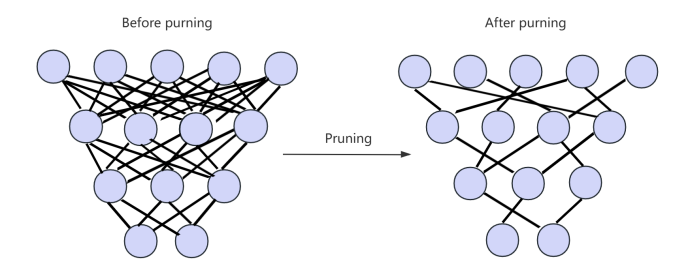
3.1. Pruning

In this section, we first review the classic weight pruning technique used in this study. Its basic process and algorithm pseudo code are shown in Figure 1 and Table 1 respectively. For a given layer \( l \) \( l \) with the weight matrix \( Wl=( \begin{matrix} w_{11} & ⋯ & w_{1n} \\ ⋮ & ⋱ & ⋮ \\ w_{n1} & ⋯ & w_{nn} \\ \end{matrix} ) \) , we calculate the threshold of weight according to the pruning percentage p, as: , we calculate the threshold of weight according to the pruning percentage \( p \)

\( τ = percentile(|Wl |, p) \) (1)

We then generate mask matrix \( Ml \) so that the weights with absolute values greater than the threshold can remain unchanged while other weights are reset to zero, as:

\( M_{ij}=\begin{cases}1, if|w_{ij}|>τ \\ 0, otherwise\end{cases} \) (2)

The updated weight matrix \( W_{l} \) is the principal element product of the original weight matrix and the mask matrix.

\( W_{l}^{,}=W_{l} ⨀ M_{l} \) (3)

Where ⨀ represents element-by-element product.

Figure 1. Visualization of pruning process.

Table 1. Pseudo code of pruning algorithm

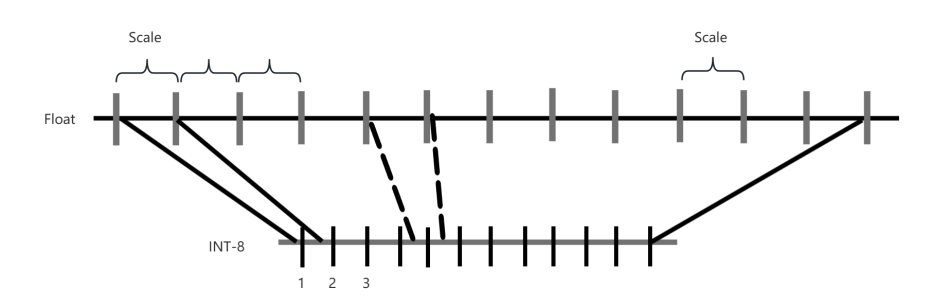
3.2. Quantization

Similar to the settings in pruning, given weight matrix \( Wl \) of layer \( l \) , the quantization algorithm calculate the maximum absolute value \( max _val \) of the elements in the weight matrix, as: \( max _val \)

\( max _val = max (|Wl |) \) (4)

Based on the maximum absolute value, the quantization scale \( S \) will be calculated, as: \( S \)

\( S=\frac{2^{num_bits}-1}{max⁡_val} \) (5)

where \( num_bits \) is the bit width of quantization. The quantized weight matrix \( W_{l}^{Q} \) can be defined as:

\( W_{l}^{Q}=⌊W_{l}×S⌉×\frac{1}{S} \) (6)

Where \( ⌊∙⌉ \) means rounding. The basic process and algorithm pseudo code of classical quantization algorithm are shown in Figure 2 and Table 2 respectively.

Figure 2. Visualization of quantization process.

Table 2. Pseudo code of quantization algorithm

3.3. Knowledge distillation

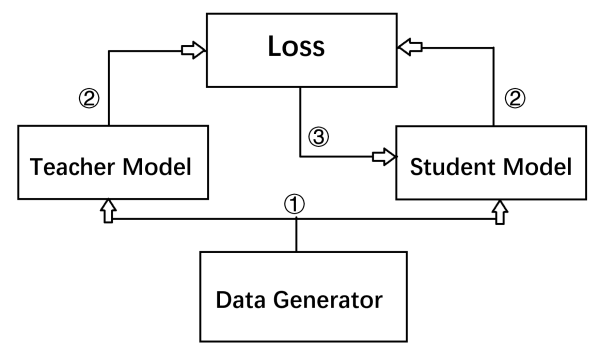
As shown in Figure 3, the knowledge distillation module is implemented as a teacher-student framework. The pseudo code of Knowledge Distillation Algorithm is illustrated in Table 3. Given the input data \( x \) , the teacher model \( f_{t} \) produces the output \( z_{t} \) , as:

\( z_{t}=f_{t}(x) \) (7)

We apply the temperature scale \( T \) to the output of the teacher model to obtain the soft label \( qt \) , as:

\( q_{t}=softmax(\frac{z_{t}}{T})=\frac{exp⁡(\frac{z_{i}}{T})}{\sum_{j}^{} exp⁡(\frac{z_{j}}{T})} \) (8)

Given the same input data \( x \) , the student model \( fs \) produces the output \( zs \) using the equation (7). The cross entropy loss \( L \) serves as the loss function for the student model, which is trained using the instructor model's soft labels.

\( L = CrossEntropyLoss(zs , qt) \) (8)

The student model parameters are optimized using the backpropagation algorithm, as:

\( θs = θs - η∇θL \) (9)

Table 3. The pseudo code of knowledge distillation algorithm

Algorithm 3 Knowledge Distillation Algorithm. \( S \) \( S \) represents the student model, \( T \) \( T \) represents the teacher model, \( D \) \( D \) denotes the data loader, \( O \) is the optimizer, ℓ is the loss function, 𝛼 is the weighting factor, and 𝑇′ is the temperature. \( O \) is the optimizer, \( l \) is the loss function, \( α \) \( α \) is the weighting factor, and \( T' \) \( T' \)

Input: student_model, teacher_model, data_loader, optimizer, loss_fn, alpha, temperature Output: average_loss distill( \( S, T, D, O, l, α, T' \) ) \( S, T, D, O, l, α, T' \) 2. Set S to training mode 3. Set T to evaluation mode \( L_{cumulative} \) ← 0 5. for each (x, y)∈D do 6. Move x, y to the computation device 7. O.zero_grad() \( y_{s} \) ← S(x)//student output 9. with no gradient computation do \( y_{t} \) ←T (x) //teacher output \( P_{t} \) ← softmax( \( \frac{y_{t}}{T} \) )//soft target \( P_{s} \) ← softmax( \( \frac{y_{s}}{T} \) )//soft output \( L_{soft} \) ← \( l(P_{s}P_{t}) \) ⋅( \( α⋅T^{2} \) ) \( α⋅T^{2} \) \( L_{hard} \) ← \( l(y_{s}y_{t}) \) ⋅(1- \( α \) ) \( α \) \( L_{total} \) ← \( L_{soft} \) + \( L_{hard} \) \( L_{total} \) .backward() 17. O.step() \( L_{cumulative} \) ← \( L_{cumulative} \) + \( L_{total} \) end for \( L_{cumulative} \) \( L_{avg} \) ← \( \frac{L_{cumulative} }{|D|} \) //average loss return \( L_{avg} \) 22. end function

Figure 3. The structure of knowledge distillation.

3.4. Mode Construction

In this study, we systematically analyzed and compared the issues of communication and model compression in Federated Learning. First, we built a baseline model based on the Fashion-MNIST dataset using a fully connected neural network. Next, we applied the three compression methods—pruning, quantization, and knowledge distillation—individually to the baseline model and evaluated their impact on the model's accuracy, size, and computation latency. To be more precise, quantization lowers computation and storage costs by decreasing the precision of model parameters, pruning reduces model parameters by eliminating unnecessary neural network connections, and knowledge distillation compresses the model by transferring knowledge from a larger teacher model to a smaller student model. After completing individual comparisons, we explored the combination of these three compression methods to identify the optimal strategy for maximizing the efficiency of Federated Learning. In this combined strategy, we applied pruning, quantization, and knowledge distillation in sequence. First, we pruned the model to significantly reduce the number of parameters, followed by quantization of the pruned model to further reduce computational and storage demands. Finally, we applied knowledge distillation to transfer the teacher model's knowledge to a smaller student model, optimizing its performance. After each training round, we used state dictionary aggregation to average the parameters of multiple models, constructing a stable and efficient global model.

4. Experiment

4.1. Dataset

The experiment leverages the Fashion-MNIST dataset, a commonly regarded standard for picture classification tasks. Fashion-MNIST comprises 70,000 28x28 grayscale photos organized into 10 categories, with 7,000 images per category. The training set comprises 60,000 photos, whereas the test set includes 10,000 images. This dataset is ideal for validating the performance and applicability of model compression methods [16].

4.2. Implement details

A simple neural network model, SimpleNN, is used as the baseline model in this experiment. SimpleNN consists of three fully connected layers: the first layer converts the 28x28 pixel input image into a 128-dimensional feature vector, the second layer compresses this feature vector to 64 dimensions, and the third layer produces a 10-category output from the 64-dimensional feature vector. Despite its simple structure, SimpleNN achieves good performance on the Fashion-MNIST dataset and serves as a suitable benchmark for studying model compression methods [17].

According to Table 4, an appropriate set of hyperparameters was selected for the experiments to balance the training speed and performance of the model. Specifically, the learning rate was set to 0.01, which usually achieves a good balance between training stability and convergence speed. The batch size was set to 64, ensuring computational efficiency and providing the model with enough samples for effective training. The momentum parameter was set to 0.9, helping to accelerate gradient descent and suppress oscillations.

Table 4. Variable Description Table

For model compression, the pruning ratio was set to 20%, meaning that 20% of the weights were removed during each pruning iteration. This aimed to reduce model complexity while maintaining performance. During quantization, model parameters were converted into 8-bit integers, significantly reducing storage requirements and computational load. In knowledge distillation, the weight coefficient for distillation loss was set to 0.5 to balance the losses of the teacher and student models, and the distillation temperature was set to 2.0, as an appropriate temperature can maximize the distillation effect. The number of training epochs was set to 20 to ensure that training was finished within a reasonable time while giving the model sufficient opportunities to learn the data's characteristics. The purpose of selecting these hyperparameters was to maximize the efficiency of training and inference while ensuring model performance. Experimental verification showed that these settings effectively support the implementation of model compression methods such as pruning, quantization, and knowledge distillation.

4.3. Experimental Results

To test the effect of different lightweight technologies on model performance, we quantitatively analyzed the accuracy, loss, latency and Transmission ratio of different models, whose findings are displayed in Table 5. The original model serves as the baseline with the highest accuracy at 93.84%, the lowest loss at 2.76, the delay of 4.21, and the transmission ratio of 1. In comparison, the Prune technique reduces the model's complexity, resulting in a slight drop in accuracy to 90.77% and an increase in loss to 4.59. However, it improves the delay to 3.82 and reduces the transmission ratio to 0.86. The Quantification method shows a similar pattern, achieving an accuracy of 91.06% and a loss of 4.88, with delay and transmission ratio values of 3.97 and 0.25, respectively. Knowledge Distillation leads to the lowest accuracy among all techniques at 88.65%, with a minimal increase in loss to 2.81, suggesting a significant simplification of the model. The delay slightly improves to 4.06, and the transmission ratio drops to 0.45.

When combining techniques, the model 5 (prune+quantification) yields an accuracy of 92.21% and a loss of 5.69, with the lowest delay recorded at 3.05 and a reduced transmission ratio of 0.25. The combination of prune and knowledge distillation (Model 6) maintains a comparable accuracy of 90.84% and a loss of 3.29, with a delay of 3.23 and a transmission ratio of 0.45. The combination of quantification and knowledge distillation technique (Model 7) shows an accuracy of 90.91%, a loss of 3.32, a delay of 4.05, and the lowest transmission ratio at 0.11. Finally, the combination of all three methods (Model 8) results in a balanced performance with an accuracy of 91.77%, a loss of 4.17, a delay of 3.06, and a transmission ratio of 0.11. All the results highlight the trade-offs between accuracy, model complexity, and resource efficiency across different model modifications.

Table 5. Comparison of quantitative experimental results of different methods

4.4. Convergence Analysis

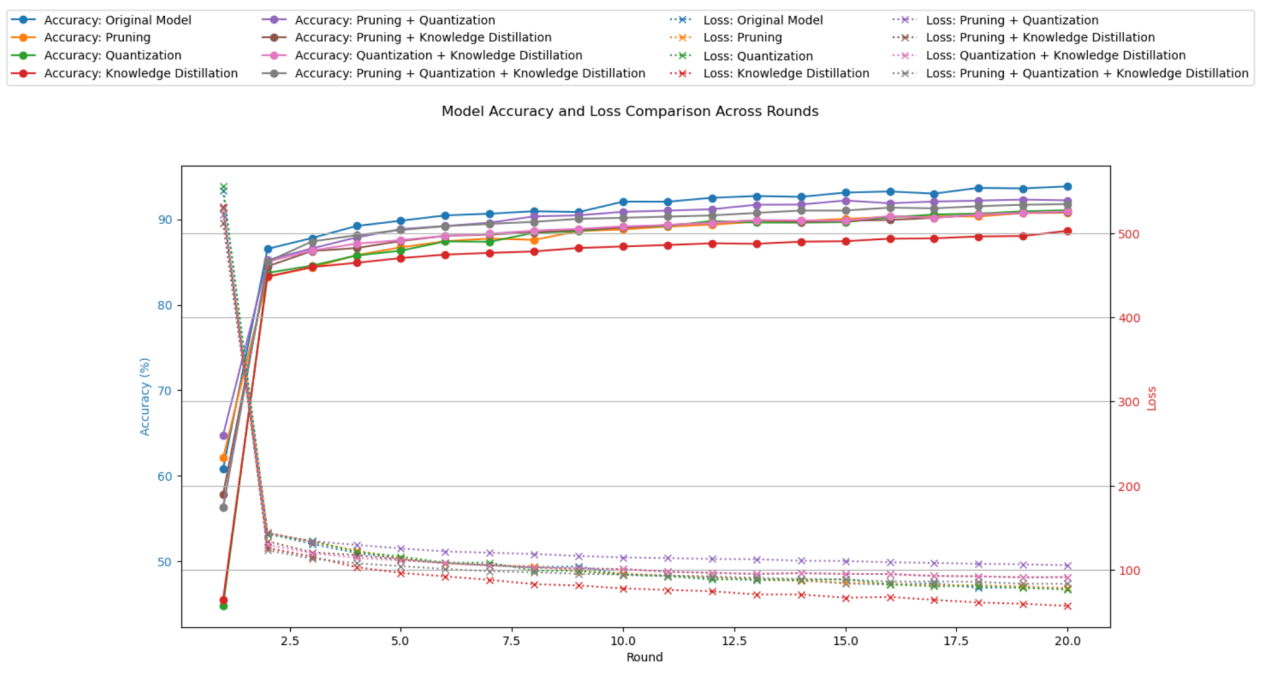
Figure 4 demonstrates varying trends in accuracy across different model optimization techniques as the rounds progress. The original model shows a consistent increase in accuracy throughout all rounds, achieving high performance without any optimizations. Techniques such as pruning and quantization impact the model's accuracy to different extents. Pruning generally leads to a slight decrease in accuracy, while quantization has a more significant impact, especially in the initial rounds, leading to greater fluctuations. Knowledge distillation starts with a lower accuracy but displays a stable upward trend, indicating moderate improvements compared to other individual techniques. The combination of pruning and quantization or pruning and knowledge distillation, generally achieve better accuracy than individual techniques, while the combination of all three techniques usually performs well, although it may not always surpass the accuracy of the original model.

Figure 4. Model Accuracy and Loss Comparison Across Rounds.

In terms of loss convergence, the original model exhibits a steady reduction in loss, indicating a consistent decrease in error rate over the rounds. Pruning shows a slower reduction in loss compared to the original model, suggesting that while it can improve efficiency, it may initially lead to a higher error rate. Quantization exhibits a similar trend to pruning, with relatively slower loss reduction, highlighting the trade-off between reducing model size and increasing error. Knowledge distillation demonstrates a more rapid convergence in loss compared to pruning and quantization alone, suggesting that transferring knowledge from a larger model can effectively reduce errors. Combined methods, particularly the combination of pruning, quantization, and knowledge distillation, show a good balance between accuracy and loss reduction.

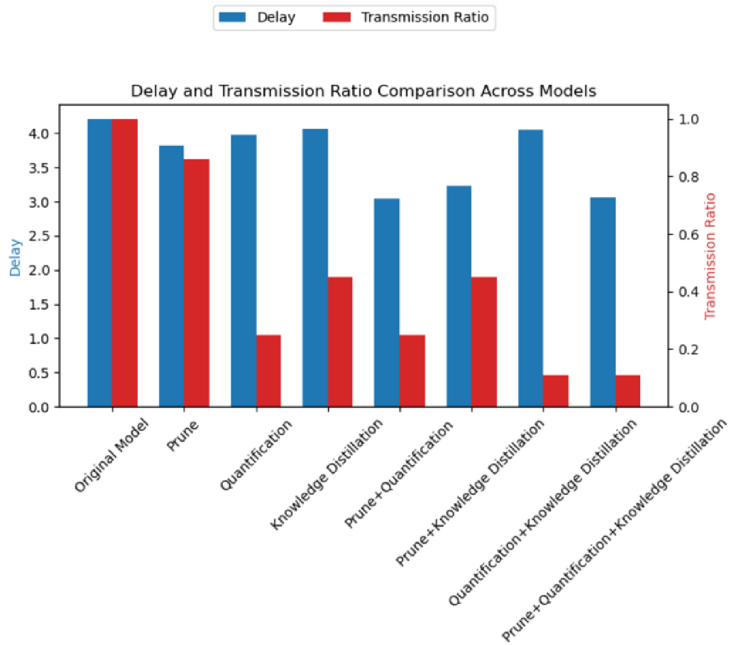
4.5. Delay and Transmission Ratio Analysis

Figure 5 presents different characteristics of delay across various models. The original model exhibits the highest delay, indicating the longest processing or transmission time, likely due to its complexity and lack of optimizations. The pruning technique shows a significant reduction in delay, demonstrating that reducing model complexity can improve data processing speed. Quantization also results in a lower delay compared to the original model, although it is slightly higher than pruning, suggesting that while quantization reduces model size, it may sometimes increase processing time. The knowledge distillation method also shows low delay, similar to pruning, indicating that model simplification and knowledge transfer effectively reduce processing time. Among the combined methods, the combination of pruning and quantization notably lowers delay, highlighting the synergistic effect of these two optimization techniques in further reducing processing time. Overall, all optimization techniques effectively reduce delay, enhancing the model's efficiency.

The transmission ratio reflects the efficiency of data transmission, with lower values indicating higher compression or transmission efficiency. The bar chart shows that the original model has a transmission ratio of 1, serving as a baseline. The pruning method significantly reduces the transmission ratio, indicating improved transmission efficiency by eliminating redundant data in the model. Quantization leads to a substantial reduction in the transmission ratio, demonstrating its superior performance in data compression. The knowledge distillation method also lowers the transmission ratio, though to a lesser extent, indicating its primary optimization impact is in reducing model complexity rather than data size. In the combined methods, especially the combination of pruning, quantization, and knowledge distillation, the transmission ratio reaches the lowest values, indicating that the joint application of these techniques maximizes data compression efficiency.

Figure 5. Delay and Transmission Ratio Comparison Across Models.

5. Discussion

The previously described experimental findings show how various optimization strategies, including quantization, pruning, and knowledge distillation, can improve model performance, especially with regard to accuracy and loss. However, the significant impact of knowledge distillation on accuracy might indicate deficiencies in the SimpleNN (simple neural network) architecture, either in network design or the knowledge transfer process. This could be due to the overly simplistic structure of the SimpleNN model, which may fail to effectively capture and represent the complex knowledge conveyed by the teacher model. We also notice that the configuration of temperature parameters and loss function design involved in the knowledge distillation process may prevent the student model from fully learning the essential content from the teacher model, thus affecting the final accuracy. Another noteworthy phenomenon is that the combination of pruning and quantization, while achieving excellent performance in terms of accuracy, also results in the highest loss. This could be because, in the SimpleNN architecture, pruning and quantization lead to extreme compression of model parameters, particularly considering the already limited number of parameters in this model. Such compression might result in the loss of crucial information. Specifically, the simplification of floating-point representation during quantization and the removal of important connections during pruning can increase model errors, thereby raising the loss.

Future research will examine the applicability of these compression strategies to a larger range of datasets and architectures, as this study only used the Fashion-MNIST dataset and a particular neural network architecture. At the same time, introducing more advanced hyperparameter optimization methods to fine-tune the balance between compression and performance is also a direction worth exploring, especially using the powerful non-deformation transformation capabilities of deep convolutional networks to model deep combinations between different methods. In addition, in order to further improve the efficiency and applicability of the model in resource-constrained environments, we will also consider federated learning collaboration between different AI chips.

6. Conclusion

This study evaluated several model compression strategies, including pruning, quantization, and knowledge distillation, and assessed their individual and combined effects on model performance and efficiency. The original model, without any compression, showed the highest accuracy and best performance across all metrics. However, its large size resulted in the highest latency and transmission ratio, making it less suitable for practical applications where resource consumption is a critical factor. We discovered that the combination of pruning, quantization, and knowledge distillation performed the best overall after examining the effects of different model compression strategies. This combination preserved high accuracy and minimal loss while also successfully reducing the model's size and computational resource requirements.