1. Introduction

With the widespread adoption of cloud computing, more and more data is being stored in the cloud. However, this also brings challenges regarding data security and searchability. To ensure data security, we need a protocol that not only guarantees the security of data stored in the cloud but also ensures its searchability, while providing users with access to the appropriate data based on their identity [1]. In current research, secure searchable encryption protocols based on attribute-based encryption (ABE) have made some progress. However, these protocols still face unresolved issues. For example, some protocols cannot simultaneously support access control strategies using “AND” gates, “OR” gates, and “threshold” gates, which limits their flexibility in practical applications [2]. Additionally, the high computational complexity of some protocols makes them difficult to implement in real-world applications.

To address these issues, further research and improvements on existing protocols are needed. First, we need to design a protocol that can simultaneously support multiple access control strategies to meet the needs of different scenarios. Second, we need to optimize the computational complexity of the protocol to ensure efficient operation in practical applications. Moreover, we must consider how to deploy and implement these protocols in real-world applications to maximize their effectiveness.

2. System Model and Security Model

2.1. System Model

The deployment of smart home systems raises concerns about security and privacy protection. Sensors collect sensitive user data, such as sleep patterns and health indicators, which are transmitted through the home network, posing security risks. Users are concerned that devices may leak private data, especially when common devices like temperature sensors transmit data to the gateway, which could be vulnerable to eavesdropping [3], as shown in Figure 1. Therefore, enhanced security measures such as encrypted communication and access control are necessary to protect user privacy and data security. Both users and manufacturers must work together to raise security awareness and ensure the system operates in a secure environment.

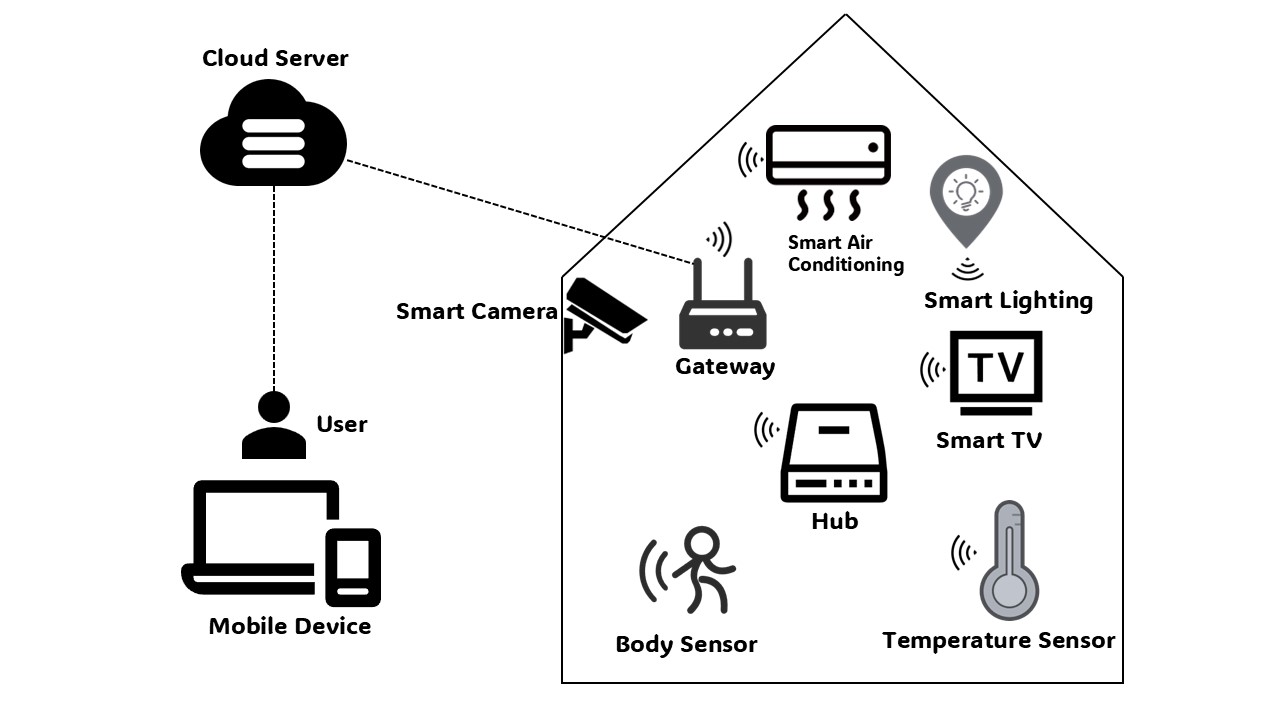
Figure 1: Smart Home Architecture

The protocol proposed in this paper is based on a system model that includes three entities: data owners, cloud servers, and data users. This system model is illustrated in Figure 2, showing the interaction of these three entities across the following three phases.

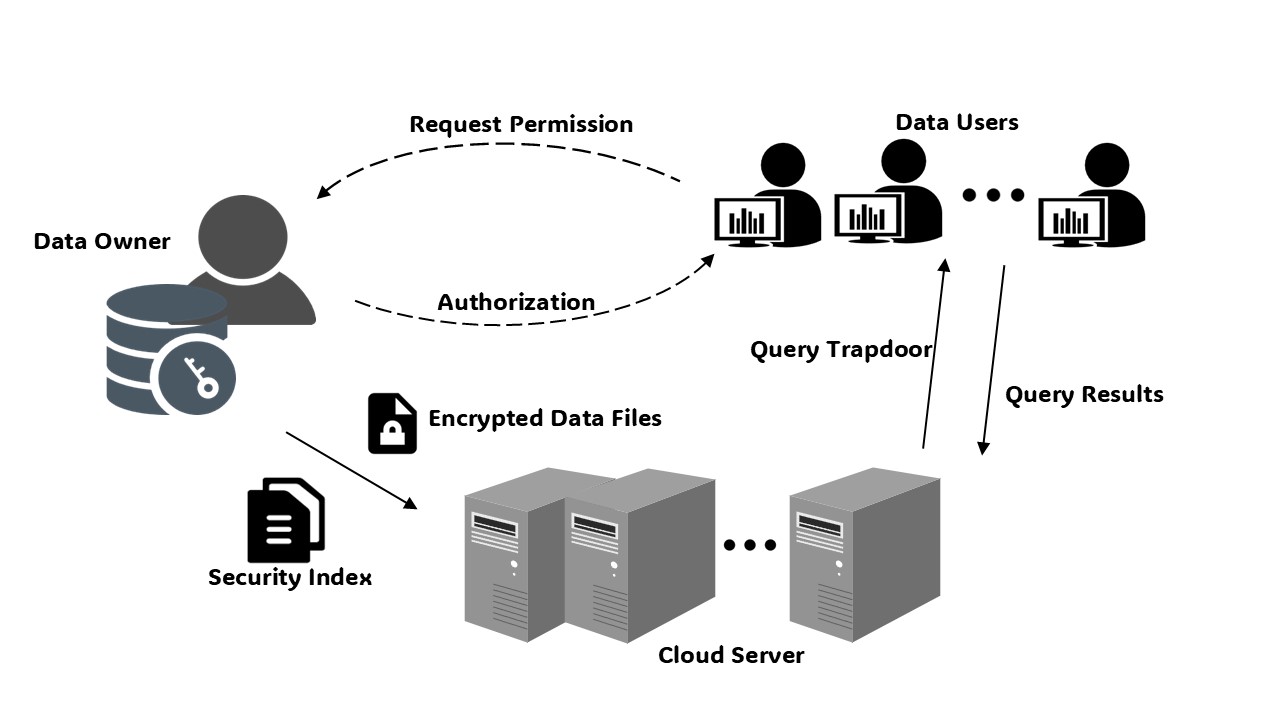
Figure 2: Single-Authority System Model

Phase 1: Data Upload and Encryption. Before uploading files to the cloud server, the data owner generates a keyword index list and encrypts it, embedding an access control tree to define the access policy. The encrypted file and index are then uploaded to the server.

Phase 2: Permission Allocation. The data user requests access from the data owner, who allocates an attribute set and key according to the user’s needs, ensuring fine-grained access control.

Phase 3: Data Retrieval. The data user uses the key to generate a trapdoor, which is sent to the cloud server to search for data. The server executes the algorithm and returns the result set, ensuring data security and user privacy throughout the process.

2.2. Protocol Definition

Before detailing the construction of the proposed protocol, this section provides a formal definition of the protocol to be introduced.

Definition 3: A single-authority, attribute-based searchable encryption protocol consists of the following five polynomial algorithms:

(1) \( (PP,{sk_{1}},{sk_{2}})←setup({1^{λ}}) \) : This algorithm is executed by the data owner to initialize the entire protocol. It takes the security parameter λ as input and outputs a set of public parameters PP that can be accessed by all entities in the system, a key set \( {sk_{1}} \) used to generate query permissions for the data users, and a key \( {sk_{2}} \) used to construct secure search indices.

(2) \( {CT_{w}}←EncryptIndex(PP,{sk_{2}},w,{T_{w}}) \) : This algorithm is invoked by the data owner to encrypt keywords in the index list. It uses the public parameters PP and the key \( {sk_{2}} \) to generate the corresponding ciphertext based on the input keyword w and the access control tree \( {T_{w}} \) , which is defined by the data owner to determine access permissions [4].

(3) \( SK←KeyGenerate(PP,{sk_{1}},S) \) : When a data user wishes to join the system and access data, they need to request permission from the authority (i.e., the data owner). The data owner determines the user’s attribute set and uses the public parameters PP and key \( {sk_{1}} \) to generate a key set SK corresponding to the data user’s permissions based on their attribute set S.

(4) \( Tr(w)←TrpdrGenerate(PP,SK,w) \) : This algorithm is executed by the data user when they want to query files corresponding to a keyword. The algorithm uses the public parameters PP and the user’s key SK to generate a trapdoor for the input keyword w.

(5) \( 1/⊥=search(PP,{CT_{{w_{0}}}},Tr(w)) \) : This algorithm is executed by the cloud server to check whether the trapdoor of the query keyword received from the data user matches the encrypted keyword in the index list. The algorithm takes the public parameters PP, the trapdoor Tr(w) of the query keyword w from the data user, and the ciphertext \( {CT_{{w_{0}}}} \) of the encrypted keyword \( {w_{0}} \) from the secure index list as input to determine whether Tr(w) and \( {CT_{{w_{0}}}} \) match. If the key SK associated with the user’s attributes matches the access control tree \( {T_{{w_{0}}}} \) in \( {CT_{{w_{0}}}} \) and w equals \( {w_{0}} \) , the algorithm returns 1, and the cloud server returns all data files corresponding to the keyword \( {w_{0}} \) to the user. Otherwise, the algorithm returns \( ⊥ \) , and the cloud server does not return any data files corresponding to the keyword \( {w_{0}} \) [5].

2.3. Security Model

The cloud server is considered “honest but curious,” meaning it provides normal services while attempting to extract user data. To ensure security, encryption algorithms are used to protect data files, and the security of encrypted and query keywords is verified through the “adaptive chosen keyword attack game” and the “chosen plaintext attack game.” These games simulate interactions between a challenger and a polynomial-time adversary to prove that the protocol can effectively prevent unauthorized users from obtaining plaintext information, thus ensuring user data privacy and security.

Definition 1: Adaptive Chosen Keyword Attack Game.

Setup: The challenger B sends the system’s public parameters to the adversary A.

Step 1: A adaptively requests a set of query trapdoors \( {q_{1}},{q_{2}},...{q_{m}} \) based on the attribute sets \( {S_{1}},{S_{2}},...{S_{m}} \) from the challenger B, as well as the ciphertexts of a set of keywords \( {w_{1}},{w_{2}},...{w_{m}} \) .

Challenge: A defines an access control tree T’ that does not match any of the attribute sets \( {S_{1}},{S_{2}},...{S_{m}} \) from Step 1. A randomly selects two keywords \( {w_{0}} \) and \( {w_{1}} \) and sends them to B along with T’. B randomly selects a number \( b∈\lbrace 0,1\rbrace \) , encrypts the keyword \( {w_{b}} \) using T’, and returns \( [{w_{b}}] \) to A.

Step 2: A queries the trapdoor for keyword q based on the attribute set \( {S_{q}} \) . The two conditions “ \( q={w_{0}}/{w_{1}} \) ” and “ \( {S_{q}} \) satisfies T’“ cannot occur simultaneously.

Guess: A guesses the value of b and outputs b’.

We denote the advantage of a polynomial-time adversary A in the above game as:

\( Adv=|Pr[{b^{ \prime }}=b]-\frac{1}{2}| \) (1)

Definition 2: Chosen Plaintext Attack Game.

Setup: The challenger B sends the system’s public parameters to the adversary A.

Step 1: A requests the ciphertexts of a set of keywords \( {w_{1}},{w_{2}},...{w_{m}} \) from B.

Challenge: A sends two keywords \( {w_{0}} \) and \( {w_{1}} \) ₁ to B. B randomly selects a number \( b∈\lbrace 0,1\rbrace \) , encrypts the keyword \( {w_{b}} \) using T’, and returns \( [{w_{b}}] \) to A.

Step 2: A continues to request a series of ciphertexts for other keywords except for \( {w_{0}} \) and \( {w_{1}} \) .

Guess: A guesses the value of b and outputs b’.

We denote the advantage of a polynomial-time adversary A in the above game similarly to Equation (1).

3. Protocol Construction

The cloud server is considered “honest but curious,” meaning it provides services while also attempting to extract data. We use encryption to protect the data and validate keyword security through secure game models, ensuring user privacy and security.

3.1. Initialization Algorithm

In the system initialization phase, the data owner first selects a cyclic multiplicative group \( {G_{1}} \) with an order of q and generator \( {G_{T}} \) , forming a bilinear map \( e:{G_{1}}×{G_{1}}→{G_{T}} \) . Additionally, two hash functions are defined during this phase:

(1) \( {H_{1}}:{\lbrace 0,1\rbrace ^{*}}→Z_{p}^{*} \) , which maps strings of arbitrary length into elements of \( Z_{p}^{*} \) .

(2) \( {H_{2}}:{\lbrace 0,1\rbrace ^{*}}→{G_{1}} \) , which maps strings of arbitrary length into elements of \( {G_{1}} \) .

Additionally, we use \( {∆_{i,S}}(x)=\prod _{j∈S,j≠i}\frac{x-j}{i-j} \) to represent the Lagrange coefficient, where S denotes a set of elements belonging to \( Z_{p}^{*} \) , and \( i,j∈Z_{p}^{*} \) . This allows us to obtain a set of public parameters \( PP=({G_{1}},{G_{T}},g,e,{H_{1}},{H_{2}}) \) . Subsequently, the data owner randomly selects two elements α and β from \( Z_{p}^{*} \) to construct two key pairs \( {sk_{1}} \) and \( {sk_{2}} \) . Ultimately, we can obtain the public parameters PP as well as the two key pairs \( {sk_{1}} \) and \( {sk_{2}} \) , as shown below:

\( \begin{cases} \begin{array}{c} PK=({G_{1}},{G_{T}},g,e,{H_{1}},{H_{2}}) \\ {sk_{1}}=(β,\frac{1}{β},{g^{α}}) \\ {sk_{2}}=(e{(g,g)^{α}},h={g^{β}}) \end{array} \end{cases} \) (2)

Here, \( {sk_{1}} \) is used to generate privileges for data users, while \( {sk_{2}} \) is used to construct a secure index list.

3.2. Keyword Index Encryption Algorithm

Constructing a secure index structure is critical to ensuring keyword information is not leaked. Keyword encryption is an effective way to achieve this goal. In a searchable encryption protocol, keyword encryption must meet two requirements: The confidentiality of keyword information must be ensured. The ciphertext structure of the keyword must be capable of effective matching detection with the trapdoor sent by the data user [6].

To satisfy these requirements, our protocol divides keyword encryption into the following two steps:

Step 1: Basic Encryption of Keyword w

For the keyword w, the data owner first invokes the hash function \( {H_{1}} \) , mapping it to an element in \( Z_{p}^{*} \) , denoted as \( {H_{1}}(w) \) . Then, it calculates \( {g^{{H_{1}}(w)}} \) , obtaining an element in \( {G_{1}} \) . Using the bilinear map e and the key \( γ=\lbrace {r_{1}},{r_{2}}\rbrace \) , the owner encodes \( {g^{{H_{1}}(w)}} \) . The ciphertext of the keyword w is then obtained as follows:

\( {ε_{r}}(w)=e{({g^{{H_{1}}(w){r_{1}}}},g)^{{r_{2}}}}=e{(g,g)^{{H_{1}}(w){r_{1}}{r_{2}}}},l={g^{{r_{2}}}} \) (3)

Here, \( γ \) can be regarded as the key used to encrypt the keyword w.

Step 2: Adding an Access Control Tree to the Ciphertext Structure of Keyword w.

The data owner defines an access control tree \( {T_{w}} \) for each keyword w, representing its access policy. For each node x in \( {T_{w}} \) , from the root to the leaf nodes, the owner selects a polynomial \( {q_{x}} \) , with the degree \( {d_{x}} \) being one less than the threshold \( {k_{x}} \) of the node x, i.e., \( {d_{x}}={k_{x}}-1 \) .

3.3. Key Generation Algorithm

In the attribute-based encryption searchable encryption protocol proposed in this paper, the process by which a data user requests query permissions reflects fine-grained access control. To achieve this, the data owner defines an attribute set for the data user based on their role and needs within the system, and then generates the corresponding key. The detailed steps are as follows:

(1) Definition of Attribute Set: The data owner first defines an attribute set S for the data user based on their real-life identity and the type of data they need access to. This attribute set S contains the names of attributes related to the user’s permissions. These attributes are assigned according to predefined system standards to ensure compliance with attribute names and values.

(2) Assignment of Attribute Values: For each attribute in the set S, the data owner assigns a corresponding attribute value based on the specific circumstances of the data user. These values are selected within the system-defined range, ensuring their validity and compliance.

(3) Generation of Attribute-Based Private Key: Using the data user’s attribute set S and the corresponding attribute values, the data owner generates the data user’s attribute-based private key with the master private key and the system’s public key. This private key is a necessary condition for the data user to decrypt the encrypted data that meets the access control policy of their attribute set.

(4) Access Control Tree: During the keyword encryption phase, the data owner defines an access control tree for each keyword. This tree describes which users, based on their attribute sets, can access the encrypted data associated with that keyword. The data user can only query the keyword if their attribute set satisfies the access control tree’s requirements.

(5) Permission Request and Verification: When a data user wants to query the data file associated with a particular keyword, they need to send a request to the data owner. This request includes the data user’s attribute set and the keyword they want to query. The data owner will verify whether the user’s attribute set satisfies the access control tree’s requirements. If it does, the data owner grants the data user permission to query the keyword and sends the corresponding trapdoor information.

(6) Trapdoor Generation and Query: Once the data user has been granted query permission, they can use their attribute-based private key and the query keyword to generate a trapdoor. The data user then sends this trapdoor to the cloud server for query. The cloud server uses the trapdoor and encrypted index for matching. If the match is successful, it returns a list of data files containing the keyword.

Through this process, the proposed protocol achieves fine-grained access control, ensuring that only users who meet specific access policies can access the relevant encrypted data files. This greatly enhances the security and control of data in cloud storage environments.

After the data owner defines the attribute set for the data user, they generate the corresponding key SK based on the attribute set as follows:

\( SK=(D={g^{\frac{α+r}{β}}},∀a∈S,{D_{a}}={g^{r}}∙{H_{2}}{(a)^{{r_{a}}}},D_{a}^{ \prime }={g^{{r_{a}}}}) \) (4)

Where r and \( {r_{a}} \) are randomly chosen elements from the non-zero integers in the p-order group, and each attribute a in S has a corresponding \( {r_{a}} \) .

Finally, the data encryption key k, keyword encryption key \( γ \) , attribute set S, and the corresponding attribute set key SK form a tuple \( (k,γ,S,SK) \) , which is sent to the data user.

3.4. Trapdoor Generation Algorithm

When a data user wishes to join the system and obtain query permission, they send a permission request to the data owner. To ensure data security and fine-grained access control, the data owner defines an attribute set for the user based on their identity and needs, and generates the corresponding attribute-based private key. This private key serves as the data user’s credential for accessing encrypted data. In the protocol proposed in this paper, whether the data user can access data files related to a specific keyword depends on whether their attribute set meets the access control tree requirements embedded in the keyword encryption structure. Only when the attribute set satisfies the access control tree can the data user obtain permission to query the keyword. This mechanism ensures that only users who meet specific conditions can access sensitive data, thereby achieving fine-grained access control and data protection.

To generate a query trapdoor that meets the aforementioned conditions, the protocol generates a keyword w trapdoor for the authorized data user as follows. The data user first calls the hash function \( {H_{1}} \) to map the keyword w to an element in \( Z_{p}^{*} \) , obtaining \( {H_{1}}(w) \) . Then, the data user randomly selects a number \( λ∈Z_{p}^{*} \) and calculates \( {g^{{H_{1}}(w)}} \) and \( {g^{λ}} \) . Next, the data user further encrypts the query keyword using the key \( γ \) obtained from the data owner for encrypting the keyword in the index list. Additionally, to verify on the server side whether the data user has access to the query keyword, the private key SK, representing their permission, is added to the trapdoor. The final trapdoor is as follows:

\( Tr(w)=({T_{1}}={g^{{H_{1}}(w){r_{1}}}}∙{g^{λ}},{T_{2}}={g^{λ∙{r_{2}}}},SK) \) (5)

Where \( {T_{1}} \) represents the encrypted form of the keyword w, and the introduction of \( λ \) ensures the unlinkability of the keyword query trapdoor.

3.5. Query Algorithm

After the data user submits the query trapdoor to the server, the cloud server executes the query algorithm to retrieve data files related to the specific keyword [7]. According to the proposed protocol, the query algorithm involves two core steps aimed at ensuring data confidentiality and fine-grained access control.

First, the server verifies whether the encrypted keyword ciphertext in the query trapdoor matches the stored keyword ciphertext in the secure index list. This step ensures that only trapdoors matching the keywords in the index list are processed, preventing interference from illegal or invalid queries.

Second, the server evaluates the permissions of the data user who submitted the query trapdoor. This involves matching the attribute set embedded in the trapdoor with the access control tree within the keyword encryption structure in the secure index list. Only if the data user’s attribute set satisfies the requirements of the access control tree are they authorized to access the data files associated with the keyword.

Only when both of these conditions are met can the data user obtain the encrypted data files related to the query keyword. Throughout the query process, the algorithm ensures that plaintext information of the data files, keyword plaintexts in the index list, and keyword plaintexts in the query trapdoor are not exposed, thus guaranteeing the system’s security. This mechanism provides effective data protection for data owners while allowing authorized data users to efficiently search for and access the data they need.

In the algorithm description, w and \( {w_{0}} \) represent the query keyword submitted by the data user and the keyword in the index list, respectively. Correspondingly, \( Tr(w) \) represents the query trapdoor for the keyword w, \( {T_{w0}} \) represents the access policy for the keyword \( {w_{0}} \) , and \( C{T_{w0}} \) represents the ciphertext structure of the keyword \( {w_{0}} \) that includes the access policy \( {T_{w0}} \) . For each leaf node x of \( {T_{w0}} \) , the following formula for \( {F_{x}} \) is obtained:

\( {F_{x}}=e{(g,g)^{r∙{q_{x}}(0)}} \) (6)

Since the root node is also a special non-leaf node, by calculating \( {F_{x}} \) for non-leaf nodes in the above manner, the root node R can ultimately be calculated as \( {F_{R}} \) , with \( {F_{R}} \) having two possible values as shown:

\( {F_{R}}=\begin{cases} \begin{array}{c} ⊥ \\ e{(g,g)^{r∙{q_{R}}(0)}}=e{(g,g)^{rs}} \end{array} \end{cases} \) (7)

If \( {F_{R}}=⊥ \) , it indicates that the user does not have the permission to query the keyword \( {w_{0}} \) . Conversely, if \( {F_{R}}≠⊥ \) , it means the user has permission to query the keyword \( {w_{0}} \) , and the server will further check if \( {w_{0}}=w \) .

After confirming the permission, the server further determines whether the query keyword w matches the keyword w₀ in the index list. During this process, the cloud server must ensure that no plaintext information related to w and \( {w_{0}} \) is obtained. This protocol verifies whether \( {w_{0}}=w \) by checking if the following equation (8) holds:

\( \frac{C}{e({C^{ \prime }},D)/{F_{R}}}∙e({T_{2}},g)=e({T_{1}},l) \) (8)

If the equation holds, it confirms that \( {w_{0}}=w \) . At this point, \( C{T_{w0}} \) and \( Tr(w) \) are considered a match.

Once it is confirmed that \( C{T_{w0}} \) and \( Tr(w) \) are a match, the cloud server returns all encrypted data files related to the encryption structure \( C{T_{w0}} \) of the keyword \( {w_{0}} \) based on the index list. After receiving the encrypted data files, the data user decrypts them using the data file key k obtained from the data owner, ultimately retrieving the plaintext of the required data files.

4. Data Transmission Protocol Analysis

4.1. Correctness Analysis

The correctness of the query algorithm directly determines the correctness of this protocol. Therefore, we will demonstrate the correctness of the protocol by proving the correctness of the query algorithm. The key to proving the correctness of the query algorithm lies in proving that the establishment of equation (8) is a sufficient condition for \( {w_{0}}=w \) . Next, I will provide a specific proof through the following derivation. First, we analyze the left side of equation (8):

\( \frac{C}{e({C^{ \prime }},D)/{F_{R}}}∙e({T_{2}},g)=\frac{{ε_{γ}}({w_{0}})∙e{(g,g)^{αs}}}{e({h^{s}},{g^{\frac{α+r}{β}}})/e{(g,g)^{rs}}}∙e({g^{λ{r_{2}}}},g)=e({g^{{H_{1}}({w_{0}}){r_{1}}+λ}},{g^{{r_{2}}}}) \) (9)

When \( {w_{0}}=w \) , we can substitute \( {w_{0}} \) with w in the equation for further analysis. The specific process is as follows:

\( \frac{C}{e({C^{ \prime }},D)/{F_{R}}}∙e({T_{2}},g)=e({g^{{H_{1}}({w_{0}}){r_{1}}+λ}},{g^{{r_{2}}}})=e({g^{{H_{1}}({w_{0}}){r_{1}}}},{g^{λ}},{g^{{r_{2}}}})=e({T_{1}},l) \) (10)

Through the derivation in equations (9) and (10), it can be proven that when \( \frac{C}{e({C^{ \prime }},D)/{F_{R}}}∙e({T_{2}},g)=e({T_{1}},l) \) , \( {w_{0}}=w \) holds, thus proving the correctness of this protocol.

4.2. Security Analysis

Discrete Logarithm (DL) Assumption: Let G be a group with generator g and order q, where q is a large prime number. We randomly and uniformly select an element \( a∈Z_{p}^{*} \) from the nonzero subgroup of integers modulo p. The DL assumption is defined as follows: within polynomial time, no adversary can compute a with non-negligible advantage \( ϵ \) given \( {g^{a}} \) and g [8]. If the DL assumption holds, the proposed protocol can achieve semantic security for query keywords under an adaptively chosen plaintext attack.

We will prove this through a “chosen plaintext keyword game” between an adversary A and challenger C.

Setup: The public parameters of the system are established as \( ({G_{1}},{G_{T}},g,e,{H_{1}},{H_{2}}) \) .

Phase 1: The polynomial-time adversary A requests query traps for keywords \( {q_{1}},{q_{2}},...,{q_{n}} \) based on the attribute set \( {S_{A}} \) . In response, C returns the query trap for keyword \( {q_{i}}(1≤i≤n) \) as follows:

\( {Tr_{A}}({w_{i}})=({T_{1}}={g^{{H_{1}}({w_{0}}){r_{1}}}}∙{g^{λ}},{T_{2}}={g^{λ∙{r_{2}}}},{SK_{A}}),(1≤i≤n) \) (11)

where \( {SK_{A}} \) is the data key corresponding to the attribute set \( {S_{A}} \) .

Challenge: A randomly selects two keywords \( {w_{0}} \) and \( {w_{1}} \) , and sends them to C. C randomly chooses a bit \( b∈\lbrace 0,1\rbrace \) , generates the query trap for \( {w_{b}} \) , and returns \( Tr_{A}^{\ \ \ }({w_{b}}) \) to A, where the specific form of \( Tr_{A}^{\ \ \ }({w_{b}}) \) is as follows:

\( Tr_{A}^{\ \ \ }({w_{b}})=(T_{1}^{\ \ \ }={g^{{H_{1}}({w_{0}}){r_{1}}}}∙{g^{λ}},T_{2}^{\ \ \ }={g^{λ∙{r_{2}}}},{SK_{A}}) \) (12)

Phase 2: A requests query traps for other keywords \( {q_{n+1}},{q_{n+2}}.... \) except for \( {w_{0}} \) and \( {w_{1}} \) .

A guesses the value of b based on the information obtained from C, with the guessed value denoted as b’. According to the previous rules, A cannot access the decryption oracle and thus cannot match the obtained query traps for \( {w_{0}} \) and \( {w_{1}} \) with the keyword decryption structure to determine b. As a result, A can only attempt to recover the value of \( {w_{b}} \) from \( Tr_{A}^{\ \ \ }({w_{b}}) \) . However, under the DL assumption, the polynomial-time adversary A cannot compute \( {H_{1}}({w_{b}}){r_{1}}+λ \) with non-negligible advantage \( ε \) , meaning that A cannot compute \( {H_{1}}({w_{b}}) \) , \( {r_{1}} \) , or \( λ \) in polynomial time. Therefore, A cannot guess b with non-negligible advantage within polynomial time. In other words, when the DL assumption holds, the probability that A guesses correctly b = b’ is \( \frac{1}{2}+ε \) , where \( ε \) is negligible.

4.3. Complexity Analysis

The computation time and output space complexity of the proposed algorithm are analyzed, as shown in Table 1:

Table 1: Complexity of Each Algorithm

4.4. Experimental Results Analysis

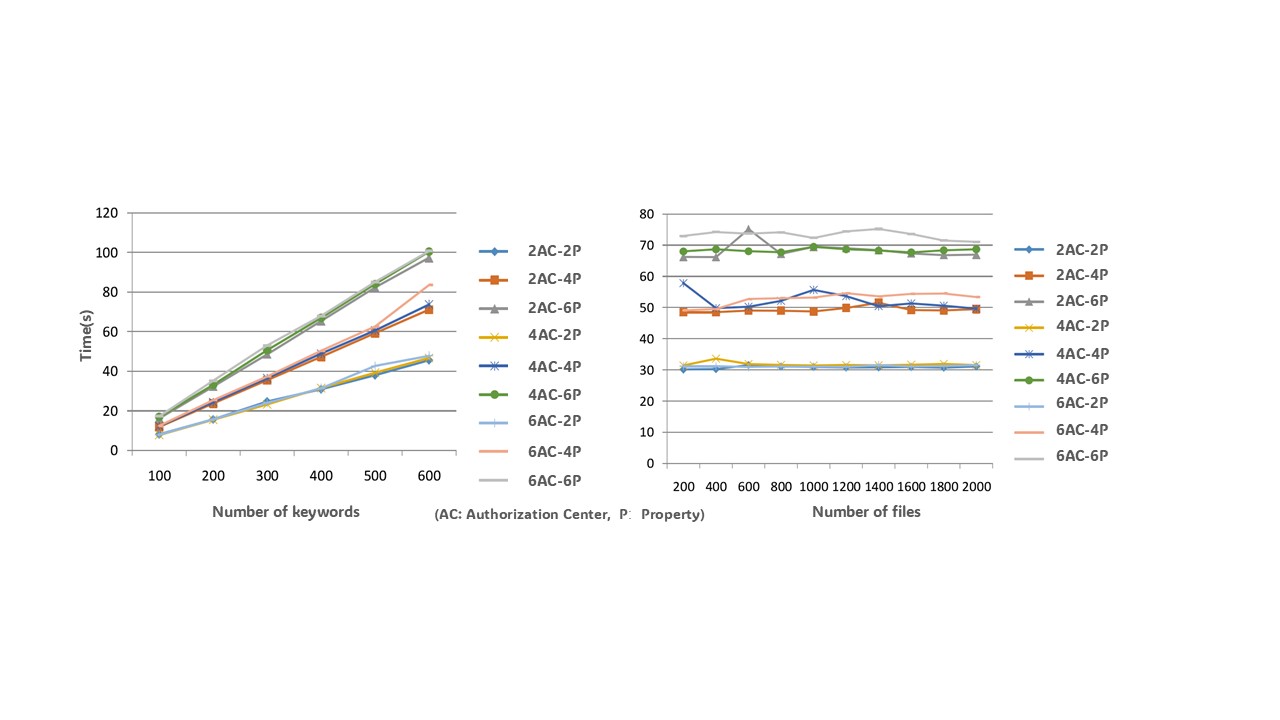
Figure 3: Query Time for Different Numbers of Indexed Keywords and User Attributes

Figure 4: Query Time for Different Numbers of Files and User Attributes

After an in-depth analysis of the data presented in Figures 3 and 4, we can clearly observe that the trend of query time for the searchable encryption protocol under multiple authorization centers is similar to that under a single authorization center. Specifically, as the number of attributes held by the data user executing the query increases, the query time for keywords also shows a growing trend. Further analysis reveals a clear linear relationship between query time and the number of keywords in the index list, meaning that as the number of keywords increases, the time required for the query also increases correspondingly. However, it is noteworthy that, compared to the total number of data files, query time does not exhibit significant correlation, indicating that the number of files does not have a substantial impact on query efficiency.

Additionally, we particularly focused on the impact of the number of authorization centers on keyword query time within the multi-authorization center architecture. The experimental results clearly indicate that regardless of how the number of authorization centers varies, there is no significant fluctuation in query time for keywords. This finding further validates the advantage of the multi-authorization center architecture in maintaining stable query efficiency.

5. Conclusion

This paper addresses the limitations of existing algorithms in the context of smart home scenarios by designing a searchable encryption protocol based on attribute-based encryption. Firstly, the security model of the protocol is clearly defined, and a formal definition is provided, laying a solid theoretical foundation for the protocol’s security. Subsequently, the paper elaborates on various key components of the protocol, including the initialization algorithm, keyword encryption algorithm, key generation algorithm, trapdoor generation algorithm, and query algorithm, ensuring that readers can fully understand the operational mechanism of the protocol.

In the theoretical analysis section, the proposed algorithm is comprehensively evaluated in terms of correctness, security, and complexity. Firstly, correctness analysis validates the protocol’s accuracy in achieving the expected functions. Secondly, security analysis ensures that the protocol can effectively resist various attacks, thereby protecting the confidentiality and integrity of the data. Complexity analysis assesses the protocol’s performance in practical applications. Finally, the applicability and advantages of the protocol in real-world applications are analyzed in conjunction with the smart home context.