1. Introduction
With the development of Multi-Agent Systems (MAS), improving their robustness in complex environments has become a research focus[1]. Traditional methods enhance system stability and anti- interference capabilities but rely on precise mathematical models and high-quality parameters. However, these methods often face limitations when dealing with uncertainties or dynamic environments. Recently, Deep Reinforcement Learning (DRL)[2], based on the Markov Decision Process (MDP), has shown great potential in addressing these challenges. Unlike traditional approaches, DRL does not require precise mathematical models. Instead, it uses a reward-punishment mechanism, allowing agents to learn and adapt through trial and error to achieve control objectives, even in the presence of interference[3,4]. This makes DRL especially suitable for handling complex disturbances and uncertainties, thereby enhancing system robustness and stability.
In MAS, agents not only interact with the environment but also collaborate or compete with each other. The Multi-Agent Soft Actor-Critic (SAC) algorithm is noted for its ability to handle continuous action spaces and multi-agent collaboration[5]. By introducing an entropy regularization term, SAC balances exploration and exploitation, improving system robustness and avoiding local optima. Given the complexity and uncertainties present in MAS environments, this study selects reinforcement learning as a solution to stabilize the multi-agent model under interference. MAS has broad applications in areas such as autonomous driving, drone swarming, intelligent manufacturing, and robot control. This study provides a new approach to MAS stability and demonstrates the adaptability of DRL in achieving control objectives without relying on precise models and high-quality parameters but only based on MDPs, even in the face of interference.
2. Methodology
This section mainly explains the model establishment of the multi-agent system with communication in the absence of interference (2.1), the control law used to achieve the goals of the multi-agent system (2.2), and the model establishment under the condition of communication interference. Finally, it elaborates on the Markov process of the anti-interference multi-agent system (2.3) and the principles of the multi-agent SAC algorithm (2.4).
2.1. Establishment of Multi-Agent System with communication
The multi-agent system considered in this paper consists of 𝑛 agents, where there is a designated leader agent. The leader agent can communicate information to other agents. In the designed multi-agent system, the leader agent communicates with the other agents, providing them with relevant information. The follower agents use the information from the leader to control their movements and reach the target position.
The communication information provided by the leader agent includes the position of the leader relative to the target. The other agents determine their own positions relative to the target by measuring their relative position to the leader agent and using the communication information provided by the leader. As a result, the follower agents are able to move towards and enter the target region. First, there are some variables defined: n represent the total number of agents in the system; \( {p_{L}}(t) \) be the position of the leader agent at time; \( {p_{T}} \) be the target position.
Base these variables, there is the mathematical formulation of the Multi-Agent System with communication:
Leader Agent's Information
The leader agent communicates its position relative to the target as follows:
\( Δ{p_{L}}(t)={p_{L}}(t)-{p_{T}}\ \ \ (1) \)
(1) Follower Agents' Control
Each follower agent measures its relative position to the leader as:
\( Δ{p_{i}}(t)={p_{i}}(t)-{p_{T}}\ \ \ (2) \)
Using the leader's communication, each follower calculates its position relative to the target:
\( {p_{i}}(t)-{p_{T}}=Δ{p_{i}}(t)+Δ{p_{L}}(t)\ \ \ (3) \)
Thus, each follower agent knows its position relative to the target and can design a control strategy to minimize the distance to the target, expressed as:
\( {u_{i}}(t)=-k({p_{i}}(t)-{p_{T}})\ \ \ (4) \)
where k is a positive constant dictating the rate of convergence towards the target.
(2) Objective:
The goal of the multi-agent system is for all agents to reach the target region, mathematically described as:
\( \underset{t→∞}{lim} ∥{p_{i}}(t)-{p_{T}}∥=0,∀i=1,2,…,n\ \ \ (5) \)
This formulation ensures that all agents eventually reach the target, using information provided by the leader and their relative positions to the leader
2.2. Proportional Navigation Guidance (PNG) Control Strategy
To ensure the followers reach the target area, we use Proportional Navigation Guidance (PNG) as the control strategy. PNG is commonly used in control systems, especially for guiding objects like missiles, where control action is proportional to the rate of change of the Line-of-Sight (LOS) to the target. Here, PNG helps followers converge to the target based on their relative position to the leader and the target.
Mathematical Formulation of the Proportional Navigation Guidance (PNG) Control Strategy:
(1) Relative Velocity and LOS Rate
We define the \( {v_{i}}(t) \) be the velocity of the 𝑖-th follower agent, \( {λ_{i}}(t) \) represent the Line-of-Sight (LOS) angle between the 𝑖-th follower agent and the target. In proportional navigation, the control input is proportional to the rate of change of the LOS angle \( {λ_{i}}(t) \) , which is influenced by the follower agent’s relative position to the leader and the target.
(2) Control Law
The control input for each follower agent is defined based on the PNG law, which is typically proportional to the closing velocity \( {v_{closing}}(t) \) (the relative speed between the agent and the target) and the LOS rate \( {\dot{λ}_{i}}(t) \) .
The control law for the can be expressed as:
\( {u_{i}}(t)=N\cdot {ν_{closing}}(t)\cdot {\dot{λ}_{i}}(t)\ \ \ (6) \)
where N is The Proportional Navigation Guidance (PNG) coefficient for the 𝑖-th agent.
(3) Determining the LOS Rate
The LOS Angle between the 𝑖-th follower agent and the target is calculated as:
\( {λ_{i}}(t)=arctan{(\frac{{y_{i}}(t)-{y_{T}}}{{x_{i}}(t)-{x_{T}}})}\ \ \ (7) \)
Where \( ({x_{i}}(t),{y_{i}}(t)) \) is the position of the 𝑖-th follower agent, and \( ({x_{T}},{y_{T}}) \) is the position of the target. The LOS rate \( {\dot{λ}_{i}}(t) \) is the time derivate of the LOS angle:
\( \dot{{λ_{t}}}(t)=\frac{\frac{d}{dt}({y_{i}}(t)-{y_{T}})({x_{i}}(t)-{x_{T}})-\frac{d}{dt}({x_{i}}(t)-{x_{T}})({y_{i}}(t)-{y_{T}})}{({x_{i}}(t)-{x_{T}}{)^{2}}+({y_{i}}(t)-{y_{T}})}\ \ \ (8) \)
(4) Convergence to the Target Region
The control law ensures that the closing velocity decreases as the agents approach the target, while proportional navigation adjusts the agents’ trajectories based on changes in the LOS rate. This allows the follower agents to steer towards the target while minimizing deviations from the desired path. By continuously adjusting their velocities using PNG control, the follower agents can converge to the target region. The system's ultimate objective is to satisfy equation .
2.3. Establishment of a Multi-Agent Model with communication interference
If there is communication interference between the leader agent and the follower agents, then the final tracking information of the follower agents to the target region will also have an error, as given by the following formula:
\( Δ{p_{i}}(t)=({p_{i}}(t)-{p_{T}})+ε(t)\ \ \ (9) \)
where: \( Δ{p_{i}}(t) \) represents the tracking error of the 𝑖-th follower agent at time t, \( {p_{i}}(t) \) is the position of the 𝑖-th follower agent at time t. \( ε(t) \) is the communication error between the leader agent and the follower agents at time t.
2.4. Markov Model of Anti-Interference Multi-Agent System
In order to train the anti-Interference multi-agent system using reinforcement learning algorithms, a Markov model needs to be established. The Markov model includes elements such as states, actions, and reward functions:
State: The positions of all agents at time 𝑡, denoted as:
\( {s_{t}}=[{p_{1}}(t),{p_{2}}(t),…,{p_{n}}(t)]\ \ \ (10) \)
Actions: The Proportional Navigation Guidance (PNG) coefficient for the 𝑖-th agent at time t, denoted as \( {a_{i}}(t) \) in the equation , it can be summarized as:
\( {u_{i}}(t)={a_{r}}(t)\cdot {ν_{closing}}(t)\cdot {\dot{λ}_{i}}(t)\ \ \ (11) \)
The reward function: The reward function is defined based on the change in distance of all agents from the target region between time 𝑡 and time t−1. The formula for the reward at time 𝑡 is:
\( r(t)=\begin{cases} \begin{array}{c} -1,if∥{p_{i}}(t)-{p_{T}}∥ \gt ∥{p_{i}}(t-1)-{p_{T}}∥ \\ +1,if∥{p_{i}}(t)-{p_{T}}∥≤∥{p_{i}}(t-1)-{p_{T}}∥ \end{array} \end{cases}\ \ \ (12) \)
In summary, by constructing the Markov model of the above anti-interference multi-agent system, the multi-agent system can still achieve its goals through adaptive decision-making, even in the case of communication interference.
2.5. Multi-Agent Soft Actor-Critic (SAC) algorithm
Through sections 2.1 to 2.4, the multi-agent system with communication interference and the corresponding Markov process are established. This section introduces the main principles of the MASAC algorithm used in this paper.
The Multi-Agent Soft Actor-Critic (SAC) algorithm is an extension of the Soft Actor-Critic algorithm designed for multi-agent systems. SAC is a model-free, off-policy algorithm based on the maximum entropy framework, which encourages exploration by maximizing the expected return while also maximizing entropy. This results in more stable and efficient learning, making it suitable for complex multi-agent environments.
(1) Entropy Regularization
The SAC algorithm uses an entropy term to encourage exploration. The objective is to maximize both the expected cumulative reward and the entropy of the policy. The entropy term is denoted as \( H(π(\cdot |s)) \) .
(2) Loss Function for Policy (Actor)
The policy update rule for the actor maximizes the expected Q-value and the entropy term, given by the following loss function:
\( {J_{x}}(θ)={E_{{s_{t}}~D,{a_{t}}~{π_{θ}}}}[αlog{({π_{θ}}({α_{t}}∣{s_{t}}))}-{Q_{ϕ}}({s_{t}},{a_{t}})]\ \ \ (13) \)
Where D is the replay buffer, \( α \) is the temperature parameter controlling the trade-off between reward maximization and entropy maximization, \( {Q_{ϕ}}({s_{t}},{a_{t}}) \) is the estimated Q-value of taking action \( {a_{t}} \) in state \( {s_{t}} \) .
(3) Loss Function for Critic (Q-function)
The critic is updated by minimizing the temporal difference (TD) error, defined as:
\( {J_{Q}}(ϕ)={E_{({s_{t}},{a_{t}},{s_{t+1}},{a_{t+1}})~D}}[({Q_{ϕ}}({s_{t}},{a_{t}})-({r_{t}}+γ{E_{{a_{t+1}}~{π_{θ}}}}[{Q_{{ϕ^{ \prime }}}}({s_{t+1}},{a_{t+1}})-αlog{({π_{θ}}({a_{t+1}}|{s_{t+1}}))}]])]\ \ \ (14) \)
(4) Temperature Parameter Update
The temperature parameter, which controls the balance between exploration and exploitation, is also updated to ensure that the policy maintains a desired level of entropy. The loss function for updating
𝛼 is given by:
\( J(α)={E_{{a_{t}}~{π_{θ}}}}[-αlog{({π_{θ}}({a_{r}}|{s_{t}}))}-α\hat{H}]\ \ \ (15) \)
Where \( \hat{H} \) is the target entropy.
3. Experiment
This section mainly conducts three experiments: the collaborative control simulation of the multi-agent system without interference, the collaborative control simulation of the multi-agent system under interference, and finally, the collaborative control training of the multi-agent system based on the deep reinforcement learning algorithm. The anti-interference capabilities of the multi-agent system in these three environments are then compared. The experiment is simulated on the device of the i5 with 12cores, the deep learning environment is Pytorch.
3.1. Experimental parameter settings
For the experiment, this section provides the physical parameters of the multi-agent system, as well as the initial states and other parameters corresponding to the interference model, as shown in Table 1. Finally, the network and training parameters of the multi-agent reinforcement learning algorithm are presented, as shown in Table 2.
Table 1: The Parameter for the physical parameters of the multi-agent system
Parameter names | Value |
Number of the agents | 5 |
Action space | [2,8] |
Interference amplitude | 10 |
Table 2: Network and training parameters of the multi-agent reinforcement learning
Parameter names | Value |
Learning Rate for network (actor/critic) | 0.0001/0.0001 |
Number of Steps per Episode | 100 |
Policy Update Frequency | Every 100 episodes |
Num of all Episodes | 1500 |
3.2. The result of the experiment
Based on the environmental parameters shown in Table 1, we conducted simulations for the multi-agent system in two environments: one without communication interference and one with communication interference, following the principles outlined in Chapter 2. The simulation results of the system are shown in Figures 1 and 2.
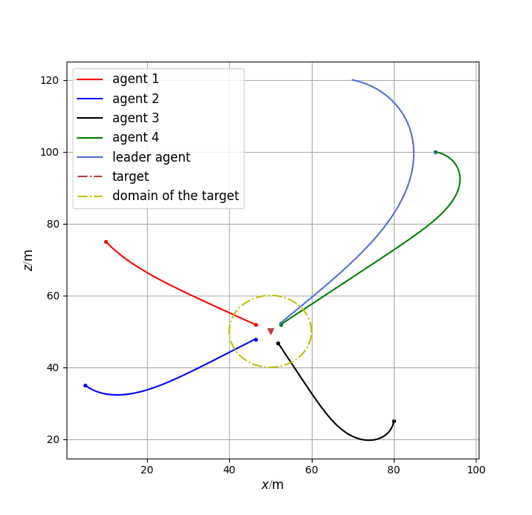
Figure 1: Multi-agent system without communication interference |
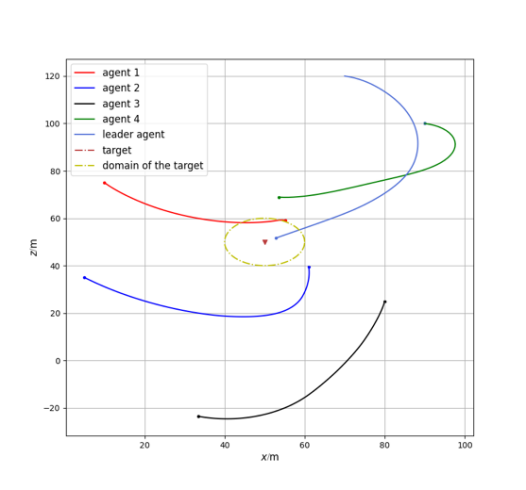
Figure 2: Multi-agent system with communication interference |
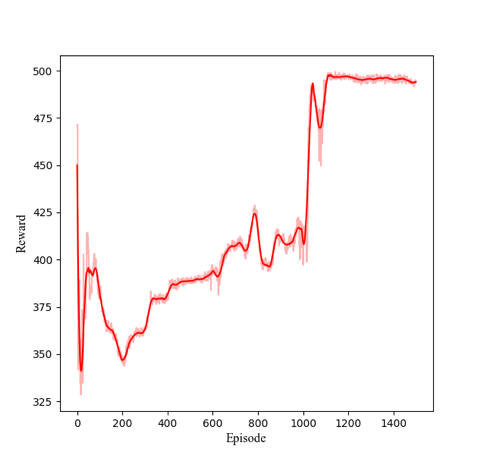
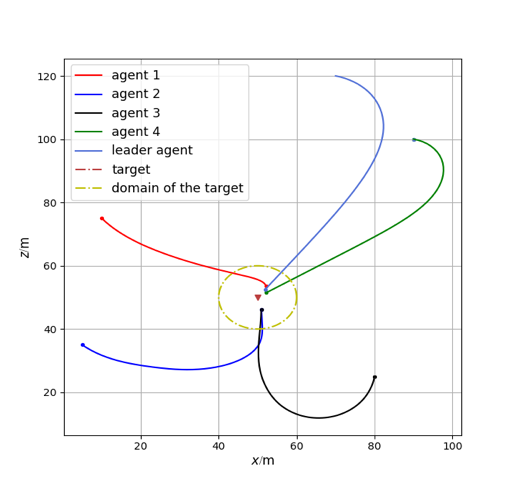
Using the reinforcement learning parameters provided in Table 2, we trained the multi-agent system with communication error interference. The reward curve of the reinforcement learning algorithm is shown in Figure 3. Applying the trained network to the environment with communication interference produced the simulation results shown in Figure 4. Additionally, the curves of the actions of each agent changing with the steps are shown in Figure 5.
Figure 3: The MASAC reward with the episode |
Figure 4: The Multi-agent system without communication interference controlled by MASAC |
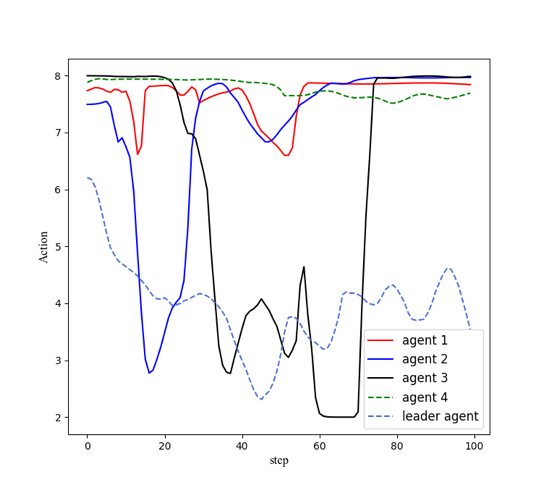
Figure 5: The actions for the 5agents controlled by the MASAC |
3.3. Results Analysist
From Figures 1 and 2, it can be seen that the multi-agent system without interference can achieve its goal, while the system with interference cannot, indicating that a multi-agent system without anti-interference algorithms cannot succeed under interference. From Figures 3 and 4, it can be observed that the reinforcement learning algorithm converges after 1500 training rounds, and the trained network effectively enables the system to achieve its goal even with interference. Combining Figure 5 with Figures 3 and 4, it can be concluded that the stable control algorithm based on reinforcement learning proposed in this paper can adaptively adjust control parameters, allowing the multi-agent system to handle communication errors and complete the task effectively.
4. Conclusion
To address the issue where a multi-agent system fails to complete control tasks under communication interference, a Markov model of the multi-agent system was established, and reinforcement learning was applied to train the model. The results show that reinforcement learning, through a reward and punishment mechanism, enables the interference-affected multi-agent system to achieve its goals. The algorithm can converge, and the trained network can effectively handle communication interference, ultimately completing the control tasks.
References
[1]. Gao, Y., Chen, S., & Lu, X. (2004). Research on reinforcement learning technology: a review. ACTA AUTOMATICA SINICA, 30(1), 86-100.
[2]. LandersMatthew, & DoryabAfsaneh. (2023). Deep reinforcement learning verification: a survey. ACM Computing Surveys.
[3]. Yang, Z. , Merrick, K. , Abbass, H. , & Jin, L. . (2017). Multi-Task Deep Reinforcement Learning for Continuous Action Control. Twenty-Sixth International Joint Conference on Artificial Intelligence.
[4]. Buoniu, L. , Bruin, T. D. , Toli, D. , Kober, J. , & Palunko, I. . (2018). Reinforcement learning for control: performance, stability, and deep approximators. Annual review in control.
[5]. Wu, L. , Wu, Y. , & Tian, Q. Y. (2023). Multiagent soft actor-critic for traffic light timing. Journal of Transportation Engineering, Part A. Systems, 149(2), 4022133.1-4022133.11.
Cite this article
Zhang,F.;Zhang,Y.;Zhao,Y.;Hou,J. (2024). Multi-Agent System Anti-Interference Algorithm Based on Deep Reinforcement Learning. Applied and Computational Engineering,99,50-55.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 5th International Conference on Signal Processing and Machine Learning
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Gao, Y., Chen, S., & Lu, X. (2004). Research on reinforcement learning technology: a review. ACTA AUTOMATICA SINICA, 30(1), 86-100.
[2]. LandersMatthew, & DoryabAfsaneh. (2023). Deep reinforcement learning verification: a survey. ACM Computing Surveys.
[3]. Yang, Z. , Merrick, K. , Abbass, H. , & Jin, L. . (2017). Multi-Task Deep Reinforcement Learning for Continuous Action Control. Twenty-Sixth International Joint Conference on Artificial Intelligence.
[4]. Buoniu, L. , Bruin, T. D. , Toli, D. , Kober, J. , & Palunko, I. . (2018). Reinforcement learning for control: performance, stability, and deep approximators. Annual review in control.
[5]. Wu, L. , Wu, Y. , & Tian, Q. Y. (2023). Multiagent soft actor-critic for traffic light timing. Journal of Transportation Engineering, Part A. Systems, 149(2), 4022133.1-4022133.11.