1. Introduction

In today's society, with the development of computer science, machine learning technology continues to mature and plays an increasingly important role in prediction and data analysis [1,2]. The prediction of the number of Olympic medals can help countries more intuitively see their strengths and weaknesses in the development of sports and provide an effective reference for athletes' pre-competition preparations [3]. As one of the important research fields of machine learning, neural networks can imitate the working principle of human neurons, learn from historical data, continuously train, filter out effective data, and make efficient predictions about the development trend of data or events [4-5].

In recent years, neural network technology has shown strong competitiveness in various prediction tasks[6,7]. Deep learning models can extract valuable information from complex features through nonlinear transformations [8,9], making them far more efficient than traditional methods when processing large-scale datasets [10,11]. By learning from historical data, this study will explore the effects of different neural network architectures and training strategies to optimize the performance of the predictive model. The model's performance will be evaluated on different datasets, and hyperparameter adjustments will be made to improve the accuracy of predictions. Neural networks can capture potential patterns and trends in complex data, providing more accurate and reliable predictions [12,13]. Compared with traditional statistical prediction methods, neural network models have a more efficient data feature processing mechanism, can cope with large-scale and high-dimensional data, and effectively model complex nonlinear relationships. This makes neural networks show great potential in medal prediction. By applying these advanced neural network technologies to Olympic medal prediction, it can provide more forward-looking decision-making support for sports administrations in various countries.

This paper explores the use of neural networks to construct a model that can reasonably predict the future trend of Olympic medals in various countries through the dataset of Olympic medals provided by Kaggle. The study will detail specific model construction methods and the final prediction effect, demonstrating the feasibility of neural networks in predicting Olympic medals. Specifically, this paper builds a prediction model based on deep learning, using information from the total number of medals won by each country in the previous Olympic Games to train a neural network model, aiming to identify and capture the performance of each country in the Olympic arena and predict the trend of the number of medals won by each country in future Olympic Games [14-16].

The experimental part will explore the effects of different neural network architectures and training strategies to optimize the performance of the predictive model.

2. Experiment

2.1. Dataset Selection

This dataset contains a large amount of medal data from the 1994 to 2024 Olympic Games (Figure 1), detailing the total number of medals awarded at the previous Summer and Winter Olympic Games, reflecting the achievements of participating countries over a 30-year period.

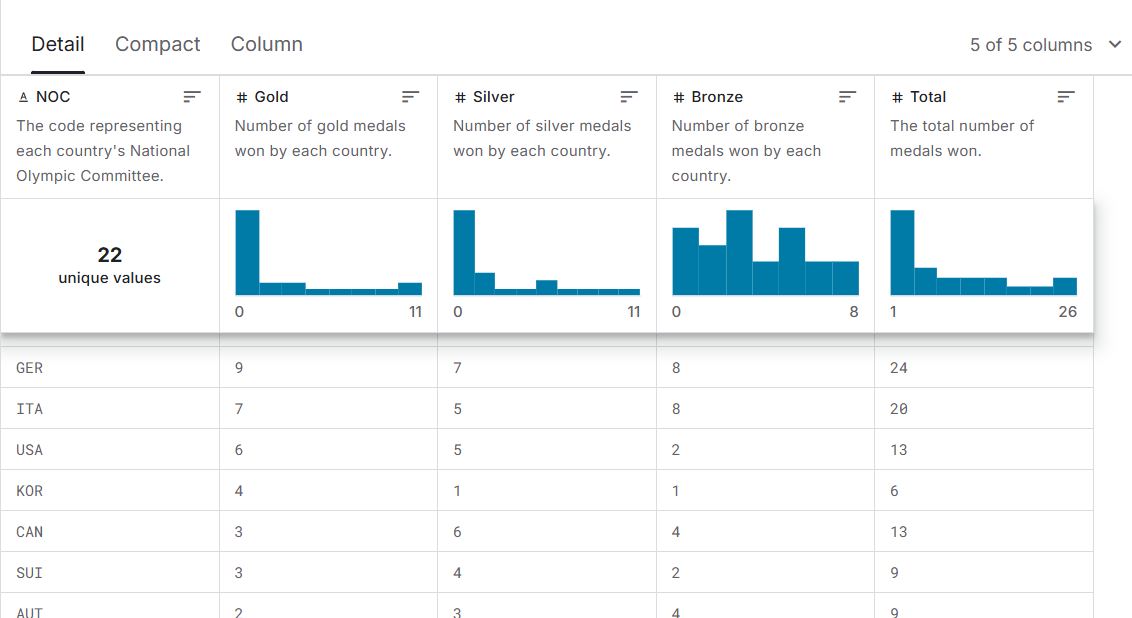
Figure 1. Dataset

2.2. Data Preparation

Firstly, the required valid data is extracted from the dataset. Since this paper only discusses the total number of medals prediction and does not discuss the medal categories, only the total number of medals is selected as a feature to train the neural network model. The data includes the total number of medals won by athletes in each sport in each country in the last four Olympic Games and is used as a standard to predict the total number of medals likely to be won at the next Olympic Games. In order to reduce the difficulty of the training process of the neural network model and obtain more concise and intuitive training results, this paper only selects the previous Olympic performances of four countries to predict. Here's an example of real data (Figure 2).

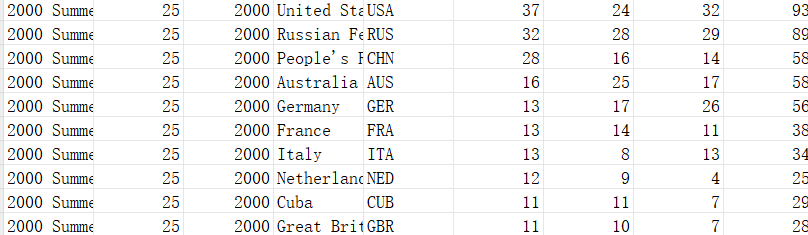
Figure 2. Real Data

2.3. Neural Network Model

We use a neural network model to make predictions. The structure of the model is as follows:

- Input Layer: The input feature is the total number of medals in each country's previous four Olympic Games.

- Hidden Layer: The model consists of two hidden layers, containing 64 and 32 neurons, respectively, and uses ReLU as the activation function.

- Output Layer: The output layer has only one output neuron that predicts the total number of medals a country will win at the next Olympic Games.

2.4. Data Preprocessing

Normalizing the eigenvalues of the selected data so that the required features have a similar range or distribution can help accelerate the gradient descent convergence, reduce the sensitivity of the model to feature scale, and improve the stability of the model training process, thereby further improving the training efficiency of the model. The 'StandardScaler' tool is used to normalize the number of medals won from previous Olympic Games to a mean of 0 and a standard deviation of 1. The data is divided into a training set and a test set, with 80% of the data used as the training set and 20% as the test set.

2.5. Model Training

For the construction of the model, the 'Sequential' model in the 'TensorFlow' library was selected to build a neural network with a relatively simple structure. The model was trained using the 'adam' optimizer and the 'mean_squared_error' loss function. The Adam optimizer combines momentum and adaptive learning rate, effectively accelerating convergence, while the mean square error (MSE) measures the prediction accuracy of the model. The model was trained for 100 rounds and validated with 20% of the data.

2.6. Hyperparameter Setting

In order to optimize the neural network prediction model, a comprehensive hyperparameter tuning strategy was carried out using the GridSearchCV toolset. During the experiment, we analyzed the impact of the number of trees on the prediction accuracy of the model when the n_estimators values were set to 50, 100, and 200. For max_depth, we evaluated the configurations of None, 10, 20, and 30 to determine the effect of tree depth on overfitting and underfitting. The min_samples_split and min_samples_leaf parameters were tested with values of 2, 5, and 10, as well as 1, 2, and 4, respectively, to balance the trade-off between model complexity and generalization ability. GridSearchCV uses a 5-fold cross-validation approach, employing negative mean square error as the evaluation criterion for the model, which helps identify the best combination of parameters.

2.7. Forecasting and Evaluation

After the model is trained, standardized real-world data features are used to make predictions about the total number of medals in the future. The mean square error (MSE) and coefficient of determination (R²) between the model's predictions and the actual performance in that Olympic Games are calculated and output. The MSE is used to measure the squared mean of the prediction error, while the R² represents the model's explanatory power for the variability of the target variable.

3. Experiment results

After model training and prediction, the following results were obtained (Figure 3).

Figure 3. Experiment Output

From the output results of the model, the mean square error of the model is 14.25, and the R² is 0.87 during the training process. This indicates that the model can explain the variability of the target variables well, and the prediction results are very close to the actual values.

4. Discussion

Through the analysis of the experimental results and the selection of appropriate hyperparameters to train the neural network model to predict the number of medals of a country in the future, the experimental output results show that the prediction performance of the model for each country has been relatively accurate. The R² value is close to 1, indicating that the model's ability to interpret and predict the selected data features has reached a basic standard. However, the mean squared error still exists, and in some cases, the predictions are not completely accurate. To further improve the model's performance, the following improvements can be considered: using more historical data to train the model and optimizing it to predict the exact type of medal. Experimenting with more complex and accurate model structures and exploring the impact of multiple hyperparameter selections on the model training process to find the best configuration. Additionally, introducing more feature variables, such as the number of athletes, the type of sport, etc., could improve the predictive power of the model.

5. Conclusion

This paper uses a neural network model to predict the number of Olympic medals and makes specific predictions for four countries: the United States, Germany, China, and Japan.

Experimental results show that the model can predict the total number of medals for each country effectively and has high explanatory power. Future research can further optimize the model and explore more feature types to improve the accuracy and reliability of predictions. This way, we can better understand the sporting strength of countries and provide valuable predictions for future Olympic events.