1. Introduction

Dynamic Difficulty Adjustment (DDA) is a mechanism in game design that allows modifying the difficulty in real-time to keep players fully engaged, according to their interactions with the environment and historical performance. The basic idea is to avoid settings that are either too simple or too hard since high difficulty can lead to frustration, while low difficulty causes boredom for players [1]. DDA can be formulated as a one-step prediction task. Such a balancing system aims to design reward functions for engagement and make predictions based on previous information. Efficiency and effectiveness are required for the system to be deployed on online and offline video game engines.

A line of studies utilizes probabilistic decision-making models to design DDA systems. Ranking systems like ELO and TrueSkill utilize interval estimation, resulting in a score on the ladder, where players with close rankings are more likely to be matched [2]. The ultimate goal is to keep the average winning rate near enough to 50% to make a fair matchmaking system. This performance evaluation system has been widely adopted in competitive games or e-sports. Advanced decision-making models are also integrated into DDA designs. The Progression Model incorporates Markov Transitions in reward calculation, selecting the best difficulty based on the decision graph [3]. Another mainstream idea for DDA systems involves training reward models based on observed experience. DL-DDA studied offline learning strategies such as clustering for different players and training deep neural networks for prediction tasks [4]. Reinforcement Learning methods like Deep Q-learning are also suitable for the task since the reward function can be linked to Q-functions in online training [5].

There are shortcomings in those two performance evaluation ideas. For probabilistic DDA systems like ELO and TrueSkill, the boundary of the confidence interval for their estimated result highly depends on the empirical variance selection for the Gaussian distribution, and depends only on one-shot experience without sufficiently exploiting each player's performance. For learning methods based on the observed data and performance, prediction models fully exploited correlations and similarities among different groups of players in DL-DDA, and historical performance with Deep Q-learning [4, 5]. However, they suffer from distribution shifts in decision-making since players act differently towards other opponents.

To find a highly adaptive and explainable algorithm for DDA, Multi-Armed Bandit (MAB) algorithms are leveraged in this study, which are simple but very powerful for algorithms that make decisions over time under uncertainty [6]. Compared to ELO and TrueSkill, MAB could simultaneously control the confidence interval and learn the true distribution for players’ performance with explainable difficulty choice. MAB is a real-time online learning method for game engines rather than neural networks with heavy parameters for offline training. Another advantage for MAB is the complete architecture of regret analysis, which reduces problems like DDA to a uniform model setting. To give a solid analysis of MAB, this study proposed a precisely balanced game engine to show whether different MAB algorithms are capable of DDA problems.

2. Method

2.1. Environment setting

A game engine was designed to simulate tournaments between two units. The engine adapts a one-player and one-monster Player versus Environment (PvE) setting. Both the player and the monster are assigned arbitrary values for \( health \) , attack \( atk \) , and defense \( def \) before their tournaments. The player attacks first, then receives damage from the monster. This is the end of a complete round. The one who loses all their health loses the game. The game engine contains a damage calculator (1) and a linear attribute generator (2).

\( d= \begin{cases} \begin{array}{c} log{(1+atk-def)(1}+ ϵ) if atk ≥ def \\ 0.1(1 + ϵ), if atk ≤ def \end{array} \end{cases},ϵ~Ν(0,{σ^{2}}) \) (1)

\( atk = \frac{1}{α} health + γ, def = \frac{1}{α} health + γ, γ~Ν(0,{τ^{2}}) \) (2)

In this damage calculator (1), results for tournaments with low attribute gaps between units are more uncertain, and the logarithm function here helps the model balance the difficulty. \( σ \) is a hyperparameter that determines the level of uncertainty for damage shift \( ϵ \) . To avoid infinite battle rounds where neither two units can deal any damage to the other, a small but normally distributed damage of around 0.1 was introduced in the calculator. The linear attribute generator (2) assumes health grows linearly with the coefficient \( \frac{1}{α} \) with the sum of \( atk \) and \( def \) with a random but small attribute shift \( γ \) , controlled by variance \( {τ^{2}} \) . This generator ensures that monsters are set at different difficulty levels and players are placed at various levels.

The concept of this PvE engine is highly extensible. For instance, players could receive higher attributes after a victory. Another adaptation could involve setting a complex environment with agents or human players. This work focuses solely on the difficulty adjustment system for static attributes to select the most appropriate opponent for players based on their performance.

2.2. Algorithms

A Multi-Armed Bandit problem is a classic framework in decision-making. The basic assumption is that a set of \( k \) arms is repeatedly selected for \( n \) times(horizons), where pulling arms does not affect the reward. The goal is to minimize the regret between the optimal and selected arm.

The idea of the algorithms is oriented towards balancing exploration and exploitation. In this game engine, four MAB algorithms were implemented: \( ϵ \) – greedy, Upper Confidence Bound(UCB1), Asymptotically Optimal Upper Confidence Bound(AOUCB), and Thompson Sampling. All four algorithms are context-free bandits, so they directly estimate the reward based on average observed rewards. Exploitation is done by pulling the arm with the best-estimated reward at each timestamp \( t \) . The main difference lies in their strategy for exploration.

\( ϵ \) – greedy does exploration with probability \( ϵ \) . With probability 1 - \( ϵ \) , the algorithm picks arm \( a=\underset{1≤i≤k}{argmax}{\hat{{r_{i}}}} \) , otherwise it explores other arms with uniform distribution.

UCB1 is designed with interval estimation for rewards. The algorithm pick arm \( a=\underset{1≤i≤k}{argmax}{\hat{{r_{i}}}} + \sqrt[]{\frac{log{1/δ}}{{N_{i}}(t)}} \) , and \( {N_{i}}(t) \) denotes that the times arm \( i \) has been picked. \( δ=\frac{1}{{n^{2}}} \) denotes the hyperparameter to control the confidence bound. It encourages exploration for arms selected fewer times and keeps confidence with more exploited arms.

AOUCB eliminates the effect of horizons on the confidence bound by picking arm \( a =\underset{1≤i≤k}{argmax}{\hat{{r_{i}}}} + \sqrt[]{\frac{2log{t}}{{N_{i}}(t)}} \) . This algorithm maintains exploration if horizon \( n \) is extremely large.

Thompson Sampling is based on Bayesian learning. It models the uncertainty of the reward for each arm by maintaining a probability distribution over possible reward values. In this approach, rewards for arms are initialized with a Beta distribution, updated as more data is gathered. At each timestamp \( t \) , the algorithm samples from these distributions and selects the arm with the largest sampled value. This process ensures that arms with higher uncertainty are sampled more, and arms with consistently high rewards are favored over time.

All four MAB algorithms are context-free multi-armed bandits, meaning they measure the difficulty of the battle without any information about the attributes of players or monsters. The key point of the experiment is to compare their capability to follow predefined strategies that balance confidence in difficulty measurement with as few simulations of suboptimal tournaments (too easy or too hard for the player) as possible. This is evaluated by cumulative regret, as discussed in Section 2.3.2 Evaluation Metrics.

2.3. Experiment design

• Player and monster generator

This experiment generated 20 players of different levels by selecting health through a uniform distribution \( U(L=100,H=200) \) . After that, the linear attribute generator initialized their attributes with \( τ \) =0.2. Similarly, five difficulties(arms) were set by generating monsters with health values of 100, 125, 150, 175, and 200, using the linear attribute generator with \( τ \) =0.05 for more stable difficulty.

At the same time, low-stat units should have chances to beat opponents with marginal attribute advantage, so the damage calculator was set with \( ϵ \) = 0.5 here. In the numerical balance test, a player from the linear attribute generator (linear coefficient=10) with 40 health has a more than 10% probability of beating another player initialized with 50 health.

• Evaluation metrics

To eliminate the effect of rounds \( r \) growing linearly with \( health \) , a normalized round formula (3) is defined using the health lower bound \( L \) :

\( {r_{L}} = \frac{r ×L}{health} \) (3)

The goal of DDA systems is to adjust the difficulty for players. Two key factors are considered to construct the reward function (4): win or lose and the game's duration. The optimal case for players is winning the game with the maximum number of rounds. Decision boundary for round reward \( {r_{2}} \) also comes from numerical engine testing, where a player with 100 health beats the opponent within 70 rounds with a 40%+ stats advantage, 150 rounds with a 20%+ advantage, and 250 rounds with a 15%+ advantage. Beyond 250 rounds, the win rate exceeds 10%, so the result of the battle is no longer stable.

\( {r_{1 }}=\begin{cases} \begin{array}{c} 1, win \\ 0, lose \end{array} \end{cases},{r_{2}}=\begin{cases} \begin{array}{c} \frac{0, 0 \lt {r_{L}}≤70 }{1, 70 \lt {r_{L}}≤150} \\ 2, 150 \lt {r_{L}}≤250 \\ 3, {r_{L}}≥250 \end{array} \end{cases},r={r_{1}}+{r_{2}} \) (4)

Performance for multi-armed bandits is evaluated by cumulative regret (5), which represents the cumulative reward gap between the best arm \( {r^{*}} \) and selected arm \( {r_{t}} \) . For all four algorithms tested, their cumulative regrets grow with a logarithm upper bound: \( O(log(m/t)) \) . The logarithm curve could be demonstrated using the average regret (6). Optimal reward \( {r^{*}} \) was 4 for the environment, and the horizon was set to 10000.

\( cumulative regret=\sum _{t=0}^{n}{r^{*}}-{r_{t}} \) (5)

\( average regret=\frac{1}{t}\sum _{t=0}^{n}{r^{*}}-{r_{t}} \) (6)

The basic idea for this reward setting comes from Flow Theory, introduced by psychologist Mihaly Csikszentmihalyi [7-9]. The right balance between the challenges and the player’s skill level helps players fully immerse and focus in the game. Too much difficulty leads to frustration, while too little leads to boredom. In this reward setting, the game engine values winning or losing less than the number of rounds in the battle.

3. Experimental results and analysis

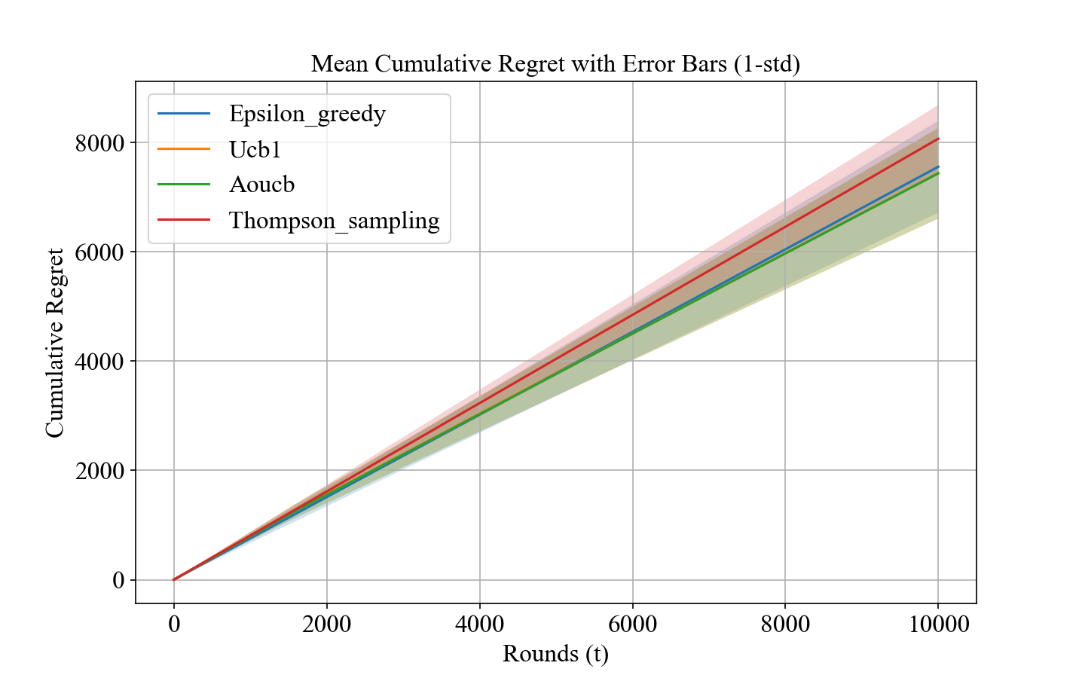
Figure 1. Cumulative regret (Picture credit: Original).

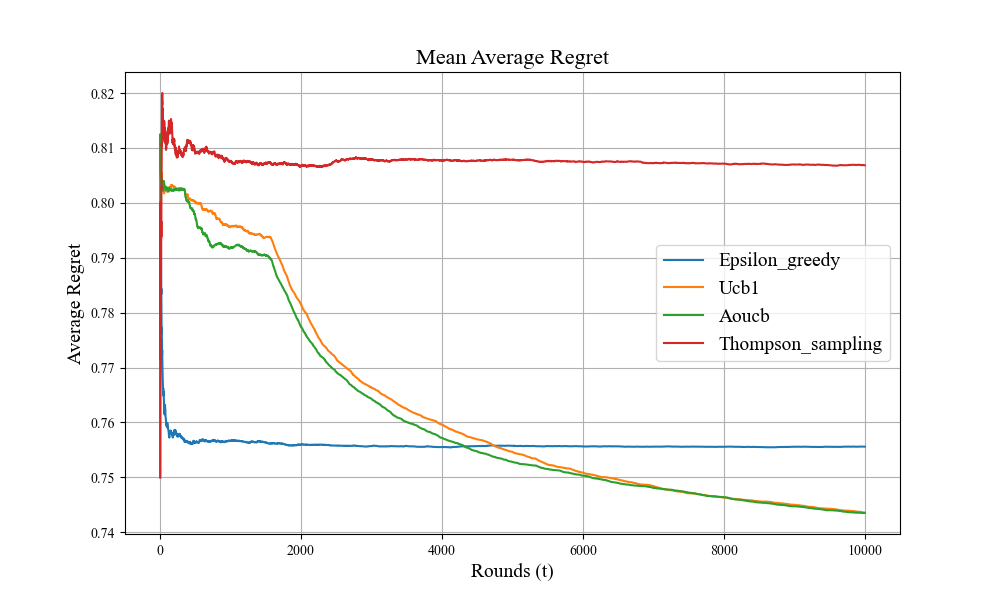
Figure 2. Average regret (Picture credit: Original).

From the cumulative regret plot Figure 1 for 20 players, all four regret curves increase linearly with the horizon. The standard variance, shown as the shaded area, is tightly bounded, indicating that Multi-Armed Bandit algorithms are stable in repeated experiments. From the average regret plot in Figure 2, all MAB algorithms successfully converged to a low average regret of less than 0.82, indicating that the algorithms successfully found the best difficulty for each player. Players win the tournaments against monsters, and the duration of the battles is at least 150 rounds on average. This demonstrates the strong adaptability of Multi-Armed Bandits in DDA systems.

In Figure 2, the convergence speed for average regret is fast for the Thompson Sampling and \( ϵ \) – greedy. DDA systems using these two algorithms found their best difficulty within 100 trials or fewer. In contrast, UCB and AOUCB kept exploring the suboptimal difficulty choice and soon realized the optimal arm within 2000 trials and did sufficient exploration on the best arm. This result indicates their strong robustness in this setting, and their exploration and exploitation balance strategy outweighs the other two algorithms, so they converge to a lower average regret in the long run.

However, from the blue curve in Figure 2, the exploration strategy for \( ϵ \) – greedy is not as effective as other algorithms. A low probability of exploration and uniform distribution for selecting other arms led to a constantly moderate value at first but failed to find the best arm in the long run. After repeatedly picking the best arm, good exploitation causes the average regret to converge to its optimal value, but this strategy did not sufficiently explore other arms, including the best arm in these experiments. This is because a fixed rate of exploration and exploitation is not as effective as adaptive strategies. After all, both UCB and Thompson Sampling adjust their confidence intervals with increasing exploitation.

Thompson Sampling is a widely used algorithm due to its computational efficiency [6]. However, in this PvE experiment, the red curve in Figure 2 indicates that the algorithm tends to have insufficient exploration, meaning the beta distribution for different difficulties is not optimal. One possible explanation is that the especially high average regret in the early rounds results from the indeterminate sampling strategy used to calculate the posterior distribution. This problem exists in the Thompson Sampling algorithm and other reward-based arm-picking policies like UCB. Further study should consider the warm-start strategy to make the algorithms more robust since the warm-up utilizes the historical data for the player’s performance with supervised learning [10, 11]. Rather than training from scratch, this method will stabilize the beta distribution for Thompson sampling, which is a more robust modification in repeated experiments.

4. Conclusion

This paper presented an effective application of Multi-Armed Bandits algorithms to Dynamic Difficulty Adjustment systems in Player versus Environment games. Through a game engine simulation, all MAB algorithms successfully find the most appropriate difficulty for players to win the battle with hundreds of rounds. UCB and AOUCB showed superior performance by efficiently selecting the optimal difficulty level within a limited number of trials. \( ϵ \) – greedy also converged to low average regret but showed an inflexible exploration strategy. No warm-up beta distribution versions of Thompson Sampling performed inconsistently for the regrets. The results of this study show the great potential of MAB algorithms in overcoming the limitations of traditional difficulty adjustment methods. By controlling exploration and exploitation through numerical boundary analysis, MAB can offer a highly explainable and computationally efficient solution for real-time difficulty adjustments in games, ensuring player engagement without sacrificing performance. Future work may apply this framework to more complex environments. The game engine could be extended with continuous settings, such as attribute rewards after battles, and build a specific combat engine like in most video games, including multiple player interactions and a skill-based evaluation system. Additionally, MAB algorithms still need improvement, such as incorporating contextual bandits or time-series methods to learn more historical information about players and implementing warm-up strategies to improve performance during the initial exploration phase, making MAB more robust.