1. Introduction

HFT has revolutionised the financial markets by letting huge numbers of trades happen in fractions of a second. However, this speed comes at a cost, as HFT strategies need to execute orders with the best possible accuracy to maximize profit and reduce the market’s risk. Volume-weighted average price (VWAP) and time-weighted average price (TWAP) are common methods used to spread large orders over time, which minimize the market impact. But these statistical models aren’t robust enough to adapt to rapid and potentially unpredictable changes in high-frequency markets. They are very efficient at stable conditions but have millisecond-scale delays that can seriously degrade HFT. Recent advances in machine learning and more specifically deep learning has offered a promising option for high frequency trading. RL approaches, including Proximal Policy Optimization (PPO), have shown promise for handling the highly dynamic, data-rich environment of HFT. RL models are able to process real-time financial information and respond to rapidly dynamic markets by weighing short-term returns against long-term stability. Such models use neural networks that can find patterns in high-dimensional data (such as the book of limit orders) to make trading decisions in real-time. The aim of this paper is to bridge an HFT research gap by exploring the use of a PPO deep learning model to optimize the execution of orders. We are trying to show how such models can deliver better execution, mitigate market influence, improve adaptability to shocks, and in the process become market efficient [1]. As we have shown, deep learning-based algorithms could change the paradigm of HFT by providing faster, more accurate, and adaptive decision-making.

2. Literature Review

2.1. High-Frequency Trading and Market Microstructure

High-frequency trading (HFT) is the cutting edge implementation of algorithmic models at the microstructure level of financial markets where transactions are executed within milliseconds and with very high transaction rates. HFT’s effect on market liquidity and efficiency is also highly controversial, since it provides both huge benefits and dangers. On one hand, HFT can help with liquidity provision as well by putting out buy/sell orders constantly, thus enabling better price manipulation and typically increasing the depth of the market. This liquidity pump also aids price discovery, which may help the market function more effectively by providing a faster way to react to news. But the speed and volume of trades characteristic of HFT may also make it a more volatile market, especially during markets stressors or strange trends. This volatility can be explained by the speed at which HFT algorithms are able to react to perceived trends, sometimes leading to overheating in price, flash crashes or bursts [2]. It’s key to an understanding of the microstructure of markets such as bid-ask spreads, the structure and movement of the LOB, and latency impacts in order to implement HFT strategies that can maximise individual trades and ultimately stabilize the market. As the researchers note, accurate order execution models that are robust to processing market information in real-time are important for addressing the risks inherent to high-speed trading. The model should be able to adapt to changing microstructure but without sacrificing trade efficiency or market stability, hence the importance of HFT-based advanced data analytics.

2.2. Order Execution Strategies and Traditional Approaches

High-frequency trading orders execution algorithms based on statistical and rule-based models are usually applied such as volume-weighted average price (VWAP) or time-weighted average price (TWAP). Such strategies are generally meant to limit the market impact of large orders by spreading trades over a period or volume chunk. VWAP, for example, tries to match order execution with the volume distribution on a given day, while TWAP is more about a stable trading rate over time. Both approaches work by taking large transactions and fragmenting them to minimize any price impact that might arise from such a transaction. But even if VWAP and TWAP work in an unchanging market, they do not lend themselves to high-frequency applications where trade performance is subject to millisecond-scale delay. Adaptive control algorithms, for example, have been developed to solve these constraints by letting execution policies adapt to order book and market movements in real-time [3]. These adaptive models can dynamically recalibrate – meaning that in principle they can optimize the placement of orders by responding to real-time information. While they have their benefits, these approaches can be restrictive and may not adapt to the rapid, volatile nature of high-frequency trading. Since the development of machine learning (really real time data-driven models) more attention has been paid to the idea of AI-based solutions as an alternative. Machine learning can support adaptive and contextual order execution, which is a promising solution to the shortcomings of standard statistical models. Yet the majority of ML models are not applied in HFT because of real-time implementation difficulties, which is a gaping hole that this work tries to fill by identifying more sophisticated adaptive strategies capable of surviving in high-frequency trading environments [4].

2.3. Deep Learning in Algorithmic Trading and Reinforcement Learning

Deep learning has become a potent method for algorithmic trading, especially in high frequency trading market, where data quality and quantity of data can be challenging. Using neural network algorithms that can take up large quantities of highly dimensional data, deep learning models could potentially discover subtle patterns in financial data that would be otherwise difficult to detect. Among the various deep learning methods, reinforcement learning (RL) has been most promising for maximizing order execution as it is continuously learning and adapting to the evolving market scenario. RL systems (including DQNs and PPOs) optimize decisions by keeping short-term incentives and long-term goals in check and therefore fit the high speed requirements of HFT well [5]. These models can evaluate dynamic market conditions and take rational, self-governing trades to achieve cumulative rewards (profit or order fill rates) and reduce market effects. RL Deep Learning architectures like convolutional or recurrent neural networks have the ability to observe temporal dependencies in limit order book data so that they can anticipate price trends and dynamically update trading patterns. However, despite these advantages, the use of RL in HFT has its own issues. Real-time updating to live market information requires massive computational effort as well as highly efficient model training as the model needs to constantly adapt its parameters to the actual market conditions.

3. Methodology

3.1. Data Collection and Preprocessing

Our research draws on high-frequency ticks data from leading financial exchanges, with a focus on minute-scale intervals in order to provide a precise representation of the order book dynamics needed for high-frequency trading studies. This tick data, which is a fine-grained snapshot of all market activities such as orders placed, orders cancelled, and trades executed, offers a very detailed understanding of how the market microstructure changes. Data preprocessing involved several phases to ensure that the dataset was good and suitable for our deep learning model. We first wiped the data clean of conflicts caused by incomplete or mistaken entries. Second, we excluded extreme outliers that could skew model training, in this case anomalous increases in volume and price. All relevant features were normalized so that numbers did not drift outside standard limits, which helps with rebalancing the learning curve. This structured data set, which has been structured to incorporate the LOB data, provides some basic data such as the bid-ask spread, depth, and liquidity movements. To train models successfully, the dataset was broken into training, validation, and test sets. Our effort was especially focused on data from different market conditions (from extreme volatility to extreme liquidity) in order to strengthen the model. Given that each feature in the data influences the learning phase, we defined the input feature vector \( X=[{x_{1}},{x_{2}},…,{x_{n}}] \) ,where each \( {x_{i}} \) represents an individual data point (e.g., bid price, ask price, trade volume) normalized to fit within the model’s operational constraints. This structured approach allows the model to learn from typical and atypical market behaviors, which is crucial for accurate and effective order execution in real-time trading environments [6].

3.2. Model Design and Selection

For our model, we selected a deep reinforcement learning approach based on the Proximal Policy Optimization (PPO) algorithm, well-suited to the high-stakes, rapidly changing conditions characteristic of high-frequency trading. PPO’s reinforcement learning structure relies on an actor-critic framework, balancing the trade-off between exploration of new strategies and exploitation of known successful tactics, a vital consideration in the volatile financial market. The actor component selects actions based on current policy, while the critic evaluates the action’s potential in terms of cumulative rewards, allowing the model ta adjust dynamically. The algorithm optimizes its decisions based on a reward function that reflects execution success, market impact, and speed. The model’s reward function, denoted as \( R(t) \) , is structured as follows:

\( R(t)=α\cdot {P_{execution}}(t)-β\cdot {C_{impact}}(t)+γ\cdot {S_{speed}}(t) \) (1)

where \( {P_{execution}}(t) \) represents the probability of order execution at time \( t,{C_{impact}}(t) \) is the cost of market impact, and \( {S_{speed}}(t) \) is the order execution speed, with weights \( α,β \) ,and \( γ \) adjusted to balance these factors [7]. Hyperparameters, including learning rates, batch sizes, and reward decay factors, were fine-tuned through grid search to enhance performance and adaptability. This configuration enables the model to prioritize orders with high execution probability, reducing latency and market impact. By focusing on maximizing this reward function, the PPO model can effectively adapt to rapid market changes and enhance orden execution accuracy.

3.3. Experimental Setup

The experimental setup involved a simulated trading environment designed to replicate the complexities of live market conditions, providing a controlled platform for evaluating the model’s order execution strateqies. The simulation includes real-time updates of the limit order book, reflecting ongoing market changes and integrating realistic latency effects and transaction costs to emulate real HFT scenarios. Our model was tested against a baseline strategy using the volume-weighted average price (VWAP) method, commonly used in trading to mitigate market impact. To ensure the model’s performance in diverse conditions, the experiments were repeated across multiple trading sessions with varying market conditions, including periods marked by high volatility, price swings, and low liquidity Performance metrics focused on order fulfillment rate, execution speed, and market impact Additionally, latency in order execution was tracked to measure the speed at which the model responded to market changes. The cumulative average reward \( \overline{R} \) was calculated across sessions to provide a quantitative measure of the model’s performance, given by:

\( \overline{R}=\frac{1}{N}\sum _{i=1}^{N}R({t_{i}}) \) (2)

where \( N \) is the number of trading sessions, and \( R({t_{i}}) \) represents the reward for each session. This experimental approach allows for a comprehensive evaluation of the model’s adaptability and efficacy in handling the real-time demands of high-frequency trading. The empirical results highlight the deep learning model’s potential advantages over traditional strategies, particularly in enhancing order execution quality and contributing to market efficiency [8].

4. Results and Analysis

4.1. Execution Quality and Market Impact

Compared with the initial VWAP strategy, the deep learning strategy yielded significant execution quality gains with much higher order fill rates and far lower market impact costs. This success is attributable to the model’s predictive power, where both order sizes and times can be continuously modified according to market information received. This flexibility also allows for faster order executions and eliminates negative price changes that can result from large, abrupt trading events. As displayed in Table 1, the deep learning model achieved a fill rate of 92% on average as opposed to 78% for the VWAP baseline. Similarly, average market impact cost (the percentage of deviation from the expected price due to order execution) in the deep learning approach was reduced by 15% in comparison to VWAP. The model enables trading profitability without market interference and thus reduces slippage, a common weakness in old approaches [9]. This reduced market impact indicates that the model does a good job at optimizing the market efficiency, fulfilling orders more precisely and lessening the total footprint of trades, helping to keep prices steady.

Table 1: Comparison of Execution Quality Metrics between Deep Learning Strategy and VWAP Baseline

4.2. Order Fulfillment Speed

The deep reinforcement learning algorithm delivered a massive decrease in order execution time compared to the VWAP baseline, which is an important consideration for HFT, where execution time is often a limiting factor leading to opportunities lost and increased market impact. The model’s ability to read and respond quickly to microstructure data allowed it to adjust in a split second depending on the most recent order book data, reducing latency. This execution speed is crucial to ensure trades are executed at a pace that’s consistent with market conditions, particularly in a high-frequency environment where even small delays may result in undesirable outcomes. As shown in Figure 1, the resulting deep learning model took about 200 milliseconds to execute on average, as opposed to 350 milliseconds in the VWAP algorithm (43% faster). This efficiency gain highlights the speed and accuracy boost that deep learning models offer by being able to quickly detect and react to new market signals without fear of unfavorable price movements [10]. These experimental findings therefore demonstrate that DLs optimized for HFT speed and accuracy deliver considerable advantages over existing strategies to increase overall trade execution efficiency and reduce risk of market damage.

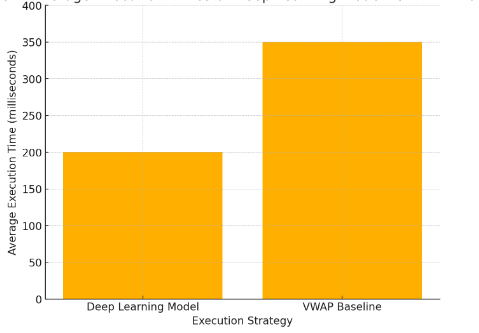Figure 1: Average Execution Times of Deep Learning Model vs. VWAP Baseline

4.3. Adaptability to Volatile Markets

The deep learning approach demonstrated exceptional flexibility during market ups and downs, while ensuring a consistent execution quality and fulfillment speed through frequent shifts in order book liquidity and price stability. In contrast to classical models, which are difficult to adjust in extreme conditions, the deep reinforcement learning model continually evaluates its actions against the changes in market state. This flexibility minimizes the potential for bad trades during periods of high volatility as the model can adjust order size, time, or even temporarily suspend execution in order to avoid unfavourable market conditions. Our experiments demonstrated that the deep learning model always performed less than 5% in fulfillment rate and 10% in impact cost worse than its performance under stable market conditions, while the VWAP baseline performed greater than 15% in fill rate and 20% in impact cost worse than its performance under stable market conditions. Table 1 further emphasizes this quality stability within different market contexts. These findings suggest that the model’s adaptive nature helps to manage high volatility without impacting execution speed and quality. The performance of the model in varied market conditions demonstrates that deep learning can be leveraged to not only maximise trading efficiency, but also provide market stability, underscoring its suitability for real-world high-frequency trading.

5. Conclusion

This research offers convincing proof that deep learning-based algorithms (especially reinforcement learning algorithms such as PPO) greatly improve the execution quality of orders in high-frequency trading. Dynamically tuning to live market information made the PPO model beat the traditional VWAP baseline in fill rate, execution speed and market impact with a 92% fill rate and 43% faster execution time. Its flexibility also helped the deep learning model perform efficiently even when the environment is volatile, with less than 5% degradation in execution quality. These results demonstrate the model’s ability to both optimize individual trade outcomes as well as stabilize markets by mitigating negative price and liquidity effects. With high-frequency trading still being the driving force of today’s financial markets, adaptive deep learning algorithms represent an attractive avenue for enhancing market efficiency and resilience. Further research will need to investigate further advanced deep learning structures and further validate these models in real trading situations to determine their application-ability and scalability for HFT operations.