1. Introduction

The earliest form of communication dates back over 3,000 years, when ancient armies used beacon towers for signaling. In the late 1960s, Chinese-American scientist Charles K. Kao proposed the feasibility of using optical fibers as a transmission medium, marking the beginning of a new era in fiber-optic communication [1]. Since then, optical communication has undergone significant development, with a focus on increasing transmission speeds, extending transmission distances, and promoting widespread application. With reductions in fiber loss and continuous advancements in laser devices and optical detectors, fiber-optic communication has experienced explosive growth, leading to the emergence of various practical fiber-optic communication systems [2]. The transmission capacity of these systems has increased by a millionfold, reflecting an unprecedented rate of development. Fiber-optic communication offers several advantages, including long transmission distances, large transmission capacities, extended repeater spacing, and high security, making it suitable for applications across a wide range of fields [3]. Today, optical fiber surpasses cable and microwave communication in various characteristics and has become the primary transmission mode in global communications [4].

With advancements in technologies such as AI, the demand for higher transmission rates and capacities has grown, leading researchers to develop multi-core optical fibers (MCFs) [5]. MCFs are fibers containing multiple cores within a single cladding. These cores are typically arranged in parallel, with each core capable of independently transmitting optical signals, allowing MCFs to transmit multiple signals simultaneously and increase transmission capacity [6]. MCFs have either widely spaced or closely adjacent cores without producing optical coupling, providing higher transmission line integration density and optical wave coupling. This makes them suitable for shorter data transmission distances [6]. MCFs are ideal for applications like local area networks and data centers, as well as in the medical field for applications such as smart skinning of aircraft, structural health monitoring of buildings, and even fiber optic gyroscope rings. The number of cores in a fiber can vary based on the type of single-mode or multi-mode fiber used. Generally, the more cores, the greater the data transmission capacity [7]. Thus, MCFs represent a promising technology for future high-capacity communication systems.

In recent years, advancements in light sources, transmission media, transmission technology, optical devices, and other related fields have collectively contributed to the overall improvement of optical networks. To enhance communication security, researchers have utilized wavelength division multiplexing technology to design an optical fiber communication network with wavelength conversion capabilities, thereby improving the network's resilience against disruptions and ensuring the reliable operation of optical fiber communication [8]. To ensure stable communication and continuous tracking of target status, an intelligent positioning method for optical communication beam positioning under high-noise conditions has been proposed. This method uses a cosine wave signal to modulate the amplitude of the beacon light. By suppressing period-dependent operations at the receiver, it enhances the signal-to-noise ratio, allowing for accurate detection of the beacon light’s beam position even under high-noise conditions [9]. In this study, an MCF network model was established, and the spatial distribution of network health status was obtained using incoherent optical frequency domain reflection and inverse Fourier transform, enabling intelligent detection of link defects in MCF networks [10].

To achieve high-speed optical communication, addressing noise generated within optical fibers is essential. Focusing on MCF optical communication, this paper proposes two schemes to suppress types of noise generated in fiber communication, thereby increasing transmission efficiency and minimizing the impact of fiber noise. MCFs contain multiple cores, which prevent optical coupling and significantly improve the transmission capacity and efficiency of optical information. By modifying the internal parameters of the MCF core, ICXT noise efficiency can be reduced, enhancing information propagation efficiency. Another innovative scheme involves adjusting the spectrum allocation of the input light, increasing wavelength spacing, and diversifying wavelength distribution to suppress phase matching conditions between cores, ultimately reducing the likelihood of FWM. These two methods effectively suppress noise generation, reduce its impact on spatial information transmission, and enhance MCF’s information propagation capabilities.

2. Application of Multi-Core Fiber in Data Centers

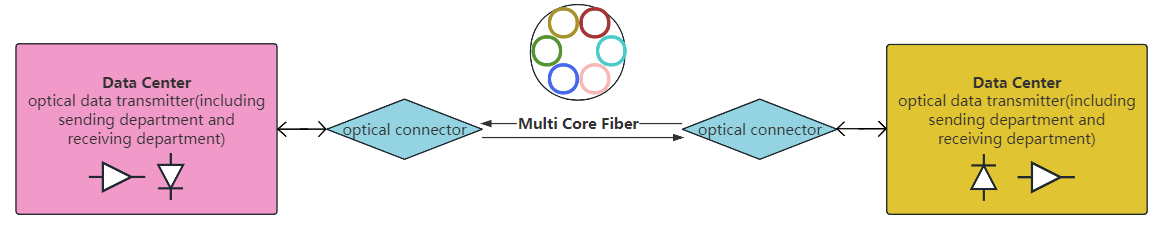
Figure 1: Data Transfer Architecture Diagram

Data centers enable the centralized processing, storage, transmission, and management of data. Inside each data center, there is an optical data transmitter, which includes both a sending and a receiving unit for initial internal data processing. Information is then transmitted between two data centers via multi-core fiber (MCF). MCFs contain multiple cores within a single cladding, allowing each core to transmit optical signals independently, which significantly increases data transmission capacity compared to traditional optical fibers. Additionally, the number of cores in an MCF can vary within single-mode or multi-mode fibers, where a greater number of cores generally corresponds to higher data transmission capacity. Information passes from the data center through an optical connector adjacent to the MCF, reaching the next data center and completing the data transfer.

3. Noise Analysis in Data Centers

While MCFs enhance the data transmission capacity and speed between data centers, noise interference within MCFs can impact transmission quality. Four-wave mixing (FWM) noise and intercore crosstalk (ICXT) noise are two prevalent types of noise in optical fibers.

FWM is a nonlinear effect based on third-order optical nonlinearity. FWM occurs when at least two different frequency components of light propagate together in a nonlinear medium, such as an optical fiber. When two frequency components, \( {ν_{1}} \) and \( {ν_{2}} \) ( \( {ν_{2}} \) > \( {ν_{1}} \) ), are present in the input light, two new frequency components (as shown in the figure below) will be generated due to the existence of refractive index modulation of the difference frequency: \( {ν_{3}} \) = \( {ν_{1}} \) - ( \( {ν_{2}} \) - \( {ν_{1}} \) )=2 \( {ν_{1}} \) - \( {ν_{2}} \) and \( { ν_{4}} \) = \( {ν_{2}} \) + ( \( {ν_{2}} \) - \( {ν_{1}} \) )=2 \( {ν_{2}} \) - \( {ν_{1}} \) . In this case, if \( {ν_{3}} \) or \( {ν_{4}} \) are present, they may undergo parametric amplification, meaning these frequency components are amplified due to the FWM effect [11].

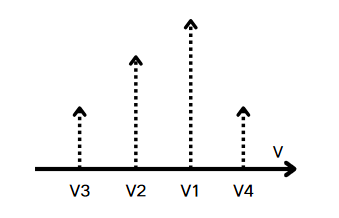
Figure 2: Schematic Diagram of Four-Wave Mixing

When three light waves of different frequencies are transmitted through the same optical fiber (a nonlinear medium), a new optical frequency component is generated due to the four-wave mixing (FWM) effect; this resulting component is known as four-wave mixed light. When three monochromatic light fields with angular frequencies \( {ν_{1}},{ν_{2}} and {ν_{3}} \) are incident in the medium, a new light field component with an angular frequency of \( {ν_{4}} \) is produced as a result of the FWM effect.

\( {ν_{4}}={ν_{1}}+{ν_{2}}-{ν_{3}} \) (1)

In a single-core optical fiber, when the polarization direction of each light field participating in the FWM is aligned and pumping depletion does not occur, the output power of the four-wave mixed light is as follows [12,13]:

\( {P_{F}}(L)=\frac{1024{π^{6}}}{{n^{4}}F_{2}^{λ}{c^{2}}}{(Dχ)^{2}}\cdot \frac{{P_{a}}(0){P_{b}}(0){P_{c}}(0)}{{A_{e{ff^{2}}}}}{e^{-aL}}{({L_{eff}})^{2}}η \) (2)

\( {L_{eff}} \) is the effective length of the fiber,

\( {L_{eff}}=\frac{1}{α}(1-{e^{-aL}}) \) (3)

\( η \) is the FWM efficiency,

\( η=\frac{{P_{F}}(Δβ≠0,L)}{{P_{F}}(Δβ=0,L)}=\frac{{α^{2}}}{{α^{2}}+{(Δβ)^{2}}}\cdot [1+\frac{4{e^{-aL}}{sin^{2}}(Δβ/2)}{{(1-{e^{-aL}})^{2}}}] \) (4)

\( {P_{F}}(L) \) represents the output power of the FWM light, and \( {P_{l}}(0) \) is the input optical power at frequency \( {f_{l}}(l=a,b,c) \) . Here, \( α \) is the attenuation coefficient of the optical fiber, \( L \) is the length of the fiber, and \( {A_{eff}} \) is the effective core area of the fiber. According to equation (4), the phase matching condition is a key factor influencing the FWM effect. When \( Δβ=0 \) , FWM efficiency reaches its maximum, a condition known as phase matching.

\( Δβ=-\frac{0_{4}^{λ}π}{{c^{2}}}\frac{d{D_{c}}}{dλ} [({f_{a}}-{f_{0}})+({f_{b}}-{f_{0}})]({f_{a}}-{f_{c}})({f_{b}}-{f_{c}}) \) (5)

In multi-core fiber (MCF), each core can independently transmit optical signals, thereby enhancing the communication capacity of the fiber optic transmission system. However, compared to traditional single-core fibers, MCFs exhibit unique inter-core crosstalk (ICXT), which can degrade the quality and communication capacity of optical signal transmission. ICXT can be mitigated through structural design adjustments, such as increasing the core spacing, enhancing the refractive index contrast between adjacent cores, or incorporating trench structures, all of which improve overall system transmission performance.

The power coupling equation for a conventional MCF is expressed as follows [15]

\( \frac{d{P_{m}}(z)}{dz}=\sum _{n≠m}^{​}{h_{mn}}(z)[{P_{n}}(z)-{P_{m}}(z)] \) (6)

In this equation, subscripts \( m \) and \( n \) represent the incident and coupled cores, respectively. \( {P_{m}}(z) \) is the average power of the incident core \( m \) . \( { P_{n}}(z) \) is the average power of the incident core \( n \) . \( {h_{mn}}(z) \) is the power coupling coefficient between the incident core \( m \) and the coupling core \( n \) . In practical weakly coupled MCFs, the power coupling coefficient \( {h_{mn}} \) varies randomly due to longitudinal random bending, torsion, and structural fluctuations. To simplify solving the power coupling equation, the average power coupling coefficient \( {\overline{h}_{mn}} \) is used instead of the instantaneous power coupling coefficient, and is expressed as [14]:

\( {\overline{h}_{mn}}=\sqrt[]{2} mn_{2}^{K}{d_{c}}[\frac{1}{\sqrt[]{a(b+\sqrt[]{ac})}}+\frac{1}{\sqrt[]{c(b+\sqrt[]{ac})}}] \) (7)

\( a=1+{(Δ{β_{mn}}{d_{c}}-\frac{{B_{mn}}{d_{c}}}{{R_{b}}})^{2}} \) (8)

\( b=1+{(Δ{β_{mn}}{d_{c}})^{2}}-(\frac{{B_{mn}}{d_{c}}}{{R_{b}}}{)^{2}}  \) (9)

\( c=1+{(Δ{β_{mn}}{d_{c}}+\frac{{B_{mn}}{d_{c}}}{{R_{b}}})^{2}} \) (10)

\( {B_{mn}}=\sqrt[]{{({β_{m}}{x_{m}}-{β_{n}}{x_{n}})^{2}}+{({β_{m}}{y_{m}}-{β_{n}}{y_{n}})^{2}}} \) (11)

In this equation: \( {K_{mn}} \) is the redefined coupling mode factor [15]. \( {β_{m }} \) is the intrinsic propagation constant of the incident core \( m \) . \( {β_{n }} \) is the intrinsic propagation constant of the coupling core \( n. Δ{β_{mn}} \) is the difference between the intrinsic propagation constant between the incident core \( m \) and the coupled core \( n \) . Due to longitudinal random bending, torsion, and structural fluctuations, the propagation constants between cores vary randomly. \( { d_{c}} \) is the related length; \( {R_{b}} \) is the bending radius of the MCF; and \( { x_{m}},{x_{n}} ,{ y_{m}},{y_{n}} \) correspond to the x, y coordinates of the core in the Cartesian coordinate system.

4. Low-noise wavelength allocation scheme analysis

4.1. FWM noise suppress scheme

Four-wave mixing (FWM) noise can be mitigated by adjusting the wavelength spacing. When three frequency components \( {ν_{1,}}{ν_{2}} \) and \( {ν_{3}} \) propagate in a nonlinear medium, such as an MCF, a new frequency component \( {ν_{4 }} \) is generated, as illustrated in Figure 1. In this scenario, the newly generated light field component with frequency \( {ν_{4 }} \) undergoes parametric amplification.

Let the zero dispersion frequency and wavelength of the optical fiber be \( {ν_{0}} \) and \( {λ_{0}} \) , respectively, \( {D_{c}} \) is the dispersion coefficient of the optical fiber, and \( {ν_{l}} \) is the frequency of the incident light field ( \( l=a,b,c \) ). In order to reduce the occurrence of FWM, the FWM efficiency \( η \) can be reduced by reducing the phase mismatch \( Δβ \) of the light field. From equation (4), it can be seen that the FWM efficiency \( η \) is proportional to the phase mismatch \( Δβ \) , and ( \( {f_{l}} \) - \( {f_{0}} \) ) determines the phase mismatch \( Δβ \) . As can be seen from equation (2), the effect of noise reduction can be achieved by reducing the optical power of the FWM by changing the wavelength interval ( \( λ=c/υ \) ). Let ( \( {ν_{a}} \) - \( {ν_{0}}) \) be the difference between the pumping optical frequency and the optical fiber dispersion frequency, \( Δλ={λ_{a}} \) - \( {λ_{c}} \) is the difference between the pumping light and the detection light wavelength, and the average zero dispersion frequency is \( { ν_{0}} \) =193.5THz.

As shown in the figure, FWM efficiency depends on the relationship between the relative pump frequency and the wavelength interval, which is the difference between the wavelengths of the pump light and the detection light.

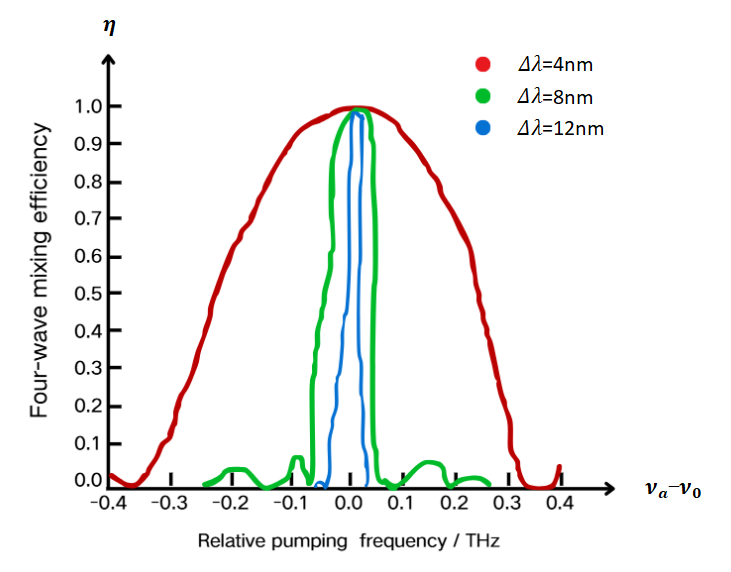
Figure 3: The Relationship Between FWM Efficiency and Wavelength Spacing [16]

When the difference between the pump light and detection light wavelengths is held constant, FWM efficiency initially increases and then decreases as the relative pump frequency rises. As shown in Figure 3, a larger wavelength interval ( \( Δλ \) ) reduces the likelihood of the FWM effect. Therefore, increasing the wavelength interval within a certain range can effectively reduce FWM noise.

4.2. ICXT Noise Suppression Scheme

ICXT noise can be suppressed by adjusting fiber length, core area, and the wavelength bands used. When a signal travels through an MCF, coupling effects and crosstalk noise arise due to the close proximity of the cores. To minimize ICXT noise within the MCF, structural modifications to the core can be implemented.

The diagram shows the relationship between the ICXT noise and the transmission distance (which can be understood as the total length of the effective fiber) under different effective core areas. (where S1<S2)

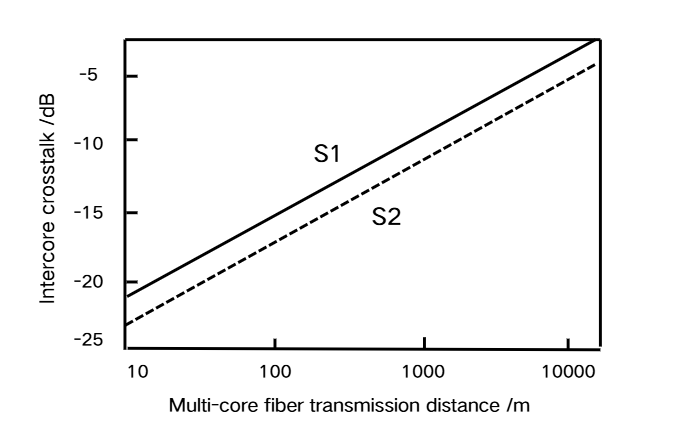
Figure 4: Direct Factors of ICXT Noise [17]

As illustrated in Figure 4, ICXT noise has a linear relationship with the effective fiber length \( { L_{eff}} \) , the longer the effective length, the more significant the crosstalk effect during signal transmission. However, increasing the effective core area \( {A_{eff}} \) reduces mode coupling, thereby decreasing core-to-core crosstalk. Thus, reducing the information transmission distance or appropriately enlarging the effective core area can help mitigate ICXT.

The wavelength band in which an optical signal propagates within the MCF also affects noise distribution. For instance, in the S-band (short band) and L-band (long band) of optical fibers, the nonlinear effects are lower, leading to a reduced power coupling coefficient \( {h_{mn}}(z) \) in equation (5) and a corresponding decrease in ICXT noise. In practical weakly coupled MCFs, the power coupling coefficient \( {h_{mn}}(z) \) fluctuates randomly due to longitudinal random bending, torsion, and structural variations, which are influenced by fiber length, core area, and nonlinearity.

In summary, to reduce FWM and ICXT noise, it is essential to optimize the information transmission network. This can be achieved by employing optical communication modes with larger wavelength spacing, shortening the effective length of the MCF, increasing the effective core area, and utilizing wavelength bands with low nonlinear effects, thereby reducing noise.

5. Experimental results and discussion

In this section, we experimentally evaluate the proposed scheme and analyze and discuss the results. For FWM noise assessment, \( Δλ= \) ( \( c/{υ^{2}} \) ) \( Δυ \) indicates the relationship between the frequency spacing of a channel and the corresponding wavelength spacing, and the Q value is a parameter that measures the quality of an optical signal. The graph below shows the relationship between channel spacing and Q value. Within a certain range, increasing the wavelength interval can reduce the noise power of FWM and improve the transmission efficiency of optical signals. Therefore, the experimental results show that our proposed scheme is effective in suppressing the FWM noise.

Figure 5: FWM rejection evaluation

For ICXT noise evaluation, the transmission power of MCFs is normalized, as shown in the figure showing the relationship between the normalized power of MCF, the transmission distance and the effective area of the fiber core. Within a certain range, reducing the optical signal transmission distance and increasing the effective core area can inhibit the generation of ICXT, thereby enhancing the transmission efficiency. Therefore, the experimental results show that our proposed scheme can effectively suppress ICXT noise.

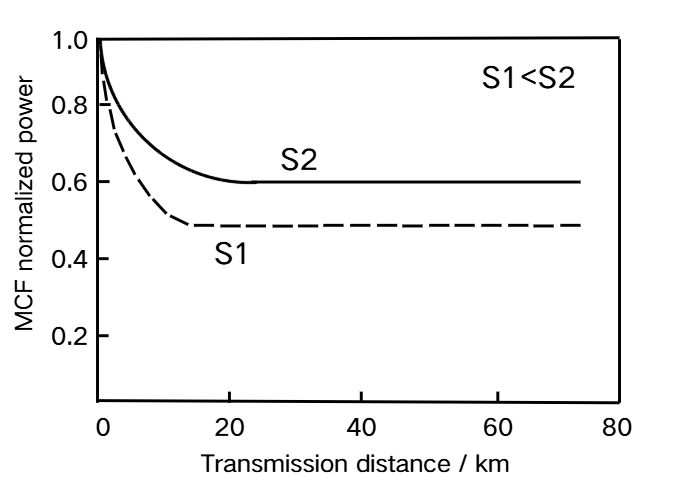
Figure 6: ICXT rejection evaluation

6. Conclusions

This paper addresses two typical sources of noise in MCF during information transmission, establishing a foundation for high-efficiency and high-capacity data propagation. During transmission in MCF, various factors can impact the rate and capacity of information transfer. By adjusting the wavelength spacing of the input optical signal and modifying the internal structure of the MCF, noise generated within the optical fiber can be effectively suppressed, ensuring smooth optical information transmission. Furthermore, the proposed scheme is evaluated to illustrate its effectiveness. The two main noise reduction strategies discussed in this paper focus on the properties of the light wave itself and the optical transmission medium, with innovative applications spanning areas such as data centers, submarine communications, and other high-capacity communication scenarios. Data centers connected by MCF play a crucial role in information transfer, and noise reduction techniques provide a solid foundation for efficient, high-capacity transmission across these endpoints. For long-distance communication lines, including submarine and aerospace communications, maintaining high-quality transmission is essential. The noise suppression techniques outlined in this paper can enhance information dissemination efficiency and optimize transmission paths in these contexts.