1. Introduction

The design of microprocessor chips is one of the core technologies in the entire computer industry, and the performance of microprocessors is constantly improving at an astonishing speed, which is driving the rapid development of the entire information industry. The multiplier is an important computing unit in microprocessors, serving as the core of real-time image processing and digital signal processing. Its computing speed determines the speed of the microprocessor. Its area affects the size of the microprocessor. The characteristics of its structure determine whether it is easy to implement in VLSI. That's why optimizing the speed, area, and structure of the multiplier is crucial for the overall performance of the microprocessor. Wallace first proposed and designed the tree multiplier structure in 1964 [1]. Several scholars proposed other typical tree multiplier structures, which have different advantages in speed and area. Many scholars have optimized these structures from multiple perspectives and achieved excellent performance.

This paper begins with an introduction to the fundamental principles and classifications of tree multipliers, including common structures such as Wallace tree and Dadda tree. Subsequently, this review delves into the diverse performance optimization strategies posited within extant literature, including the design of novel compressors, the refinement of tree structures, and the implementation of more advanced adders for the final summation. The paper concludes by summarizing the current development in the field, providing a valuable reference for subsequent studies.

2. Analysis of typical tree structures

2.1. Wallace tree

Wallace noted that while it is possible to add two or more numbers within a single adder, the growth in logical complexity is not proportional to the increase in speed, making it an impractical solution. A novel approach involves utilizing a pseudo adder, which can add three numbers together but yields two outputs instead of one. This reduces the number of remaining digits to be added, hence the term ‘3-2 Compressor’ or ‘Carry Save Adder (CSA)’. Since it can operate along its digital stages without carry propagation, it operates faster than traditional adders.

Furthermore, Wallace highlighted that employing multiple pseudo adders for parallel operation can decrease the number of digits by 1.5 times. By achieving a significant enhancement in computational speed while avoiding an increase in hardware costs, it also simplifies the control circuitry. Wallace employed this methodology in the design of tree-structured multipliers.

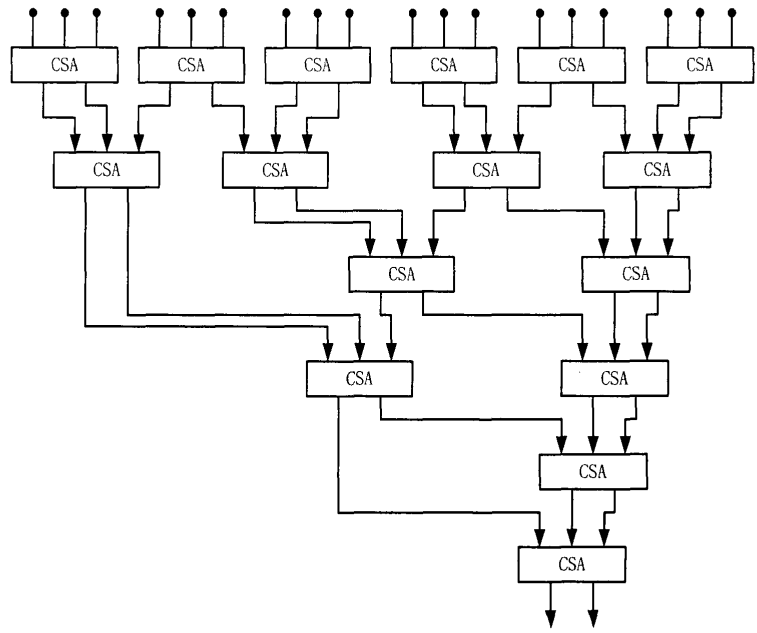
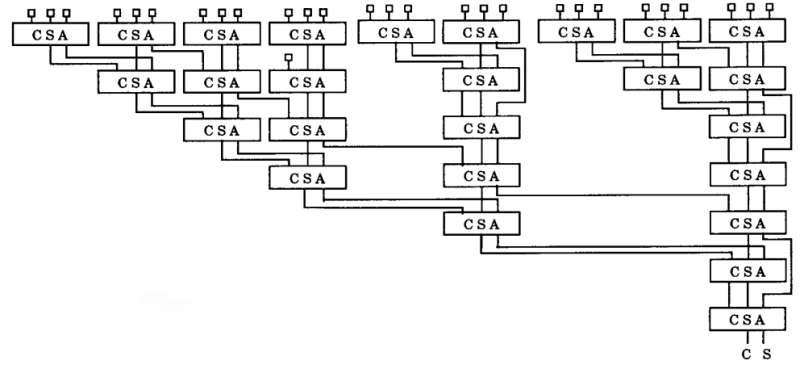
The Wallace tree multiplier comprises three phases. The initial phase involves the formation of a partial product matrix. The second phase entails the reduction of the height of this partial product matrix to two through parallel operations. The final phase employs a carry-propagate adder to combine the two rows. Figure 1 below shows the addition tree as designed in the Wallace tree architecture. Figure 2 shows dot diagram for an 8 by 8 Dadda multiplier.

2.2. Dadda tree

Dadda introduced an alternative classical structure for parallel multipliers [2]. In the design, Dadda replaces Wallace's pseudo-adder with ‘parallel (m, n) counters’. These counters are characterized by having ‘m’ inputs and ‘n’ outputs, where ‘m’ is less than or equal to ‘n’. The binary value represented by the ‘m’ outputs corresponds to the count of ‘1’s present among the ‘n’ inputs. The Dadda tree multiplier, akin to the Wallace tree multiplier, operates through three distinct stages; however, Dadda's approach employs the minimal number of (3, 2) and (2, 2) counters at each level during the partial product reduction phase. Dadda invented the dot diagram, and the figure 2 above shows the 8 by 8 multiplier designed by Dadda. This multiplier requires four reduction levels, with matrix heights of 6, 4, 3, and 2, respectively The points connected diagonally in the figure represent the output of the (3,2) counter. The two points connected by cross diagonals represent the output of the (2,2) counter. A total of 64 AND gates, 35 (3,2) counters, 7 (2,2) counters, and a 14 bit carry propagation adder are required to form a 16-bit product.

Dadda further hypothesized that counters of varying dimensions could be feasibly implemented. The 4-2 compressor has excellent characteristics, including outstanding balance and symmetry. Related studies have shown that the multiplier composed of 4-2 compressors has good performance [3]. It has been widely used as a fundamental element in tree multiplier architectures.

Habibi and Wintz believe that Dadda's method of placing counters is optimal [4]. Townsend's research shown in table 1 also indicates that under the exclusive use of (3,2) and (2,2) counters, Dadda tree multipliers exhibit reduced delay, suggesting a superior speed, along with a lower complexity compared to Wallace tree multipliers [5].

Table 1: The comparison of delay and complexity between Dadda tree and Wallace tree.

2.3. ZM tree

Zuras and McAllister proposed a method for constructing balanced delay trees, which has a better area-time product than binary tree [6]. Figure 3 shows the structure of ripple chain.

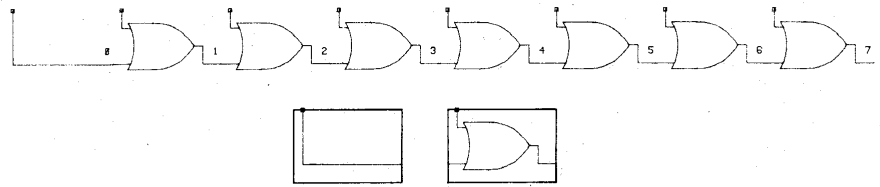
Figure 3: The structure of ripple chain.

The number represent the accumulated gate delay. Zuras and McAllister decomposed the ripple chain into sub-chains and then serially combined the results of these sub-chains. This structure shown in figure 4 introduces limited additional layout complexity but offers substantial acceleration.

Figure 4: Second-order balanced delay tree.

When the total delay of the up chain equals that of the down chain, a delay balance is achieved. If 64 inputs are to be combined to produce a single result, this structure, utilizing 2 wires, would incur 11 delays. The ripple circuit, despite having only one wire, would incur 63 delays. A binary tree, with only 6 delays, necessitates 6 wires. Zuras and McAllister demonstrated that a k-order ZM tree can accomplish the tasks of a 2k-order binary tree, albeit with higher latency, yet it saves nearly half of the area.

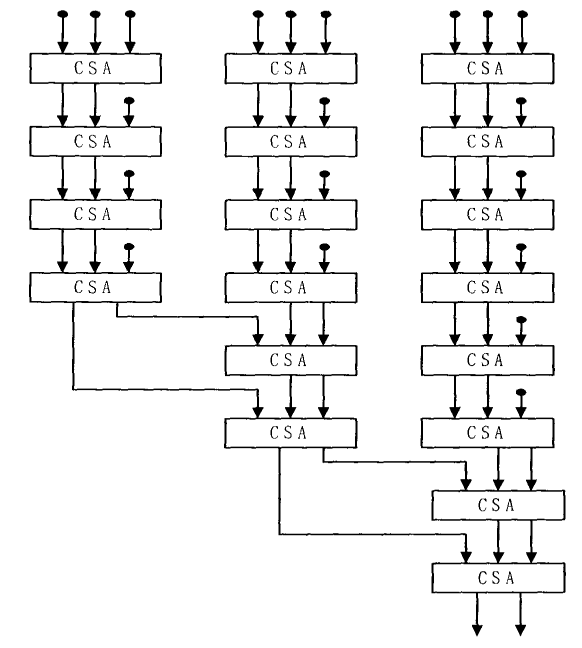
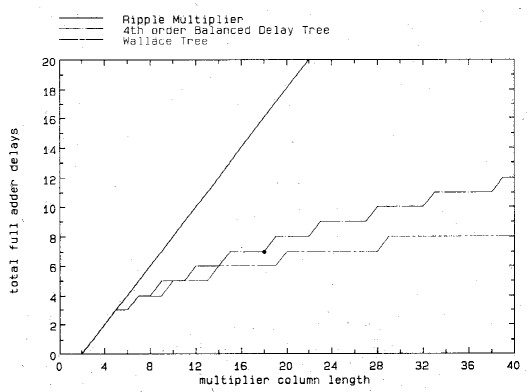
Its structure is very regular and requires very few macro modules, making it highly valuable for use. The figure 5 shows the ZM tree multiplier structure. In the research shown in figure 6 conducted by Zuras and McAllister, it was observed that the delay performance of the fourth-order balanced delay tree gradually deteriorates in comparison to the Wallace tree. However, it demonstrates significant advantages in optimizing the performance of small-scale multipliers.

2.4. OS tree

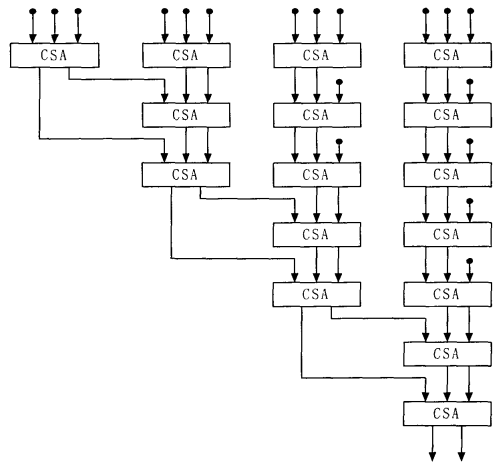
Mou and Jutand invented an 'Overturned Stairs' tree, which has a regular and compact layout resulting from their recursive structure [7]. Taking a first-order OS tree shown in figure 7 as an example, it is divided into a subject and a root, and the subject can be constructed recursively. A first-order OS tree can add N operands in \( O((2N{)^{\frac{1}{2}}}) \) time, requiring 3 TLWs. By connecting first-order OS Trees through a linear structure, one can derive higher-order OS Tree. The figure 8 shows the structures of second-order OS tree multiplier.

In the study shown in table 2 conducted by Mou and Jutand, it was observed that, compared with 4-2 tree, second-order and third-order OS tree have excellent performance. In addition, combining OS tree of different orders with ZM tree can achieve better performance. Higher order ZM tree perform poorly.

Table 2: The maximum number of operands that can be added by trees of height n.

2.5. Comparison of different tree structures

The iterative CSA array and the Dadda tree represent two extremes in the realm of arithmetic circuits. The former is characterized by its conventionality, albeit at the expense of speed; conversely, the latter offers superior speed but poses significant implementation challenges. Various other tree structures necessitate a delicate balance between operational velocity and chip area. ZM tree and OS tree sacrifice speed performance, require more latency and area. But their circuit structure is more regular, which is more conducive to the implementation of VLSI.

The author compared various structures composed of CSA that compressed 18 partial products and focused on studying some key factors. Among them, the additional unbalanced path refers to the path that requires additional waiting time, which is related to the operation speed and hardware utilization efficiency of the multiplier. Cross unit connections are closely related to layout design, and the fewer the number, the more regular the layout. Simultaneously, the hardware resource consumption of these structures was calculated. The study shown in Table 3 found that in structures using CSA as the basic addition unit, the Wallace tree has the fastest speed but but its structure is the most irregular. The running speed of OS tree is faster than ZM tree of the same order, but it has more cross cell connections and is not as regular as ZM tree. If a 4-2 compressor is used as the basic addition unit, the delay of these structures will be reduced. However, considering the structure of the 4-2 compressor itself, the delay of the tree structure has not been significantly improved. It is worth noting that the impact of cross cell wiring on the area is limited, as the wiring can often be placed on top of the device. The number of basic addition units and their own structural size have the greatest impact on the area. Therefore, based on the data in Table 3, the ZM tree uses more CSAs, which means a larger area. The OS tree improves the regularity of the Wallace tree structure without affecting the area.

Table 3: The comparison between typical structure.

3. Optimization and Analysis of Tree Structure

3.1. Challenge

The Wallace tree multiplier is renowned for its exceptional speed. However, an examination of the circuit architecture of carry-save adder reveals that the delay introduced by XOR gates is significantly greater, resulting in a longer delay for the SUM output compared to that of the CARRY output. Furthermore, the process by which the carry-save adder compresses three input bits into two is inherently unbalanced. This imbalance contributes to the irregular structure of Wallace tree multipliers, which are predicated on CSA, thereby rendering them susceptible to issues such as clock skew and constraining their applicability in VLSI environments. Designing a basic unit with good performance is challenging.

Researchers have sought to enhance performance of multipliers through several avenues: refining the Booth algorithm, exploring alternative algorithms, designing circuits with superior performance characteristics, or optimizing the adder configurations utilized in the final summation of multipliers. The challenge lies in designing a regular circuit structure that makes the multiplier easy to implement, while also having good speed performance and a smaller area.

3.2. Researches on Optimization

The conventional 3-2 compressor is characterized by a delay of two XOR gates along its critical path. Veeramachaneni has refined the architecture of the 3-2 compressor, thereby reducing the time required for transistor switching along the critical path [8]. Specifically, Veeramachaneni substitutes the first XOR gate with an XOR-XNOR configuration and replaces the second XOR gate with a MUX. In contrast, the traditional 4-2 compressor comprises two CSAs and exhibits a delay corresponding to four XOR gates along its critical path. The research conducted by Hsiao et al. has optimized the structure of the 4-2 compressor, resulting in a reduction of its delay to that equivalent to three XOR gates [9]. Similar to the 3-2 compressor, Veeramachaneni employs XOR-XNOR and XOR techniques to enhance the structural efficiency of the 4-2 compressor, resulting in a reduction of the critical path delay to two MUX and one XOR gate. Likewise, the architecture of the 5-2 compressor can be optimized using the same methodology, yielding a critical path delay of three multiplexers and one XOR gate. Some scholars have designed and optimized compressors with high compression ratios, which exhibit superior performance characteristics. Rouholamini refined the architecture of the conventional 7-2 compressor, resulting in a reduction of the critical path delay from seven XOR gates to six, thereby achieving enhanced operational speed [10].

Table 4: The comparison between different compressor.

The author compared the hardware resource consumption and delay of structures that compress 17 partial products and 22 partial products using different compressors. For ease of comparison, it is assumed that a 3-2 compressor consists of 2 XORs and 1 MUX, with a delay of 2 XORs. A 4-2 compressor consists of 4 XORs and 2 MUXes, with a delay of 3 XORs. A 5-2 compressor consists of 6 XORs, 2 MUXes, and 2 additional logic circuits with a delay of 4 XORs. A 7-2 compressor consists of 10 XORs and 5 MUXes, with a delay of 6 XORs. The research shown in table 4 above shows that various compressors seem unable to reduce hardware resource consumption. Note that the delay here is in XOR units. When the number of partial products is appropriate, mixing compressors with different compression ratios can bring advantages.

Numerous scholars choose to use a mixture of compressors with different compression ratios to optimize the Wallace tree structure for instance, Shangshang Yao designed a Wallace tree structure that utilizes a combination of 3-2, 4-2, and 5-2 compressors to compress 13 partial products [11]. In this structure, the first stage uses four 4-2 compressors, the second stage uses two 3-2 compressors, and the third stage uses one 5-2 compressor. The number of XOR gates is 23, the number of binary data selectors is 11, the compression level is 3, and the delay is 9 XORs. Compared with traditional Wallace tree, its critical path delay is significantly reduced. Zhongmin Zhao integrated CSAs and 4-2 compressors to compress 18 partial products when designing the Wallace tree structure [12]. The first stage uses CSA, the second stage uses 4-2 compressors, the third stage uses CSA, and the fourth stage uses 4-2 compressors. This structure is relatively complex, but it can effectively utilize hardware resources and improve summation efficiency. Its relatively regular structure avoids the imbalance of delay.

Dunshan Yu proposed a new structure for delay balanced tree [13]. Dunshan Yu first points out that the TLW between subtrees cannot accurately indicate the complexity of connecting lines, as the TLW of the first-order ZM tree and OS tree composed of 4-2 adders are both 2. Dunshan Yu proposed using the TLWT (Trans Layer Wires of Tree) of the entire tree to measure the complexity of connections. The calculation method is as follows.

\( TLWT=\sum _{i=1}^{n-1}TL{W_{i}}×B{C_{i}} \) (1)

In the formula, n is the number of subtree, TLW is the number of connecting lines between adjacent subtrees, and BC is the minimum number of 4-2 compressors in adjacent subtrees. The TLWT of the OS tree is 12, and the TLWT of the ZM tree is 10. And the TLWT of the Wallace tree that completes 32-bit addition is 34. Therefore, TLWT can effectively demonstrate the complexity of connections in various trees. Dunshan Yu proposed a tree with a width of 2 and a structure as shown in the figure 9. Its TLWT is 8, which is lower than ZM tree and OS tree, and its regularity is also better.

Figure 9: Proposed structure of tree multiplier.

Ykuntam et al. have chosen to utilize parallel prefix adders (PPAs) to combine the partial products of the last row with the sum from the preceding stage [14]. Table 5 below shows their analysis of fast Wallace tree multipliers designed with various PPAs, including Kogge-Stone adder, Sklansky adder, Brent-kung adder, Ladner-Fischer adder, and Han-Carlson adder. The analysis reveals that these configurations attain a reduction in latency without substantially augmenting the area. Among them, Kogge-Stone adder used more resources and occupied more area, but achieved faster speed. In contrast, Brent-kung used less area but also achieved satisfactory speed. In conclusion, the utilization of PPAs in Wallace tree multipliers presents a viable strategy for optimizing both speed and area, and the choice of PPA should be guided by a thorough understanding of the trade-offs involved.

Table 5: The comparison between different compressor.

4. Conclusion

This article introduces various typical tree multiplier structures and their performance, and compares them. It was found that the Dadda tree has the best speed performance but is difficult to implement due to its irregular circuit structure and require a large area, while the delay balanced tree circuit is regular and easy to implement but sacrifices speed performance. Among them, the ZM tree has a higher delay but has advantages in small-scale multipliers. The performance of higher-order OS tree is closer to that of Wallace tree. Over the years, many scholars have optimized the structure of compressors, designed novel multiplier addition array structures, and used better performing adders to achieve final summation, overall optimizing the speed and area performance of tree multipliers. The optimization strategies discussed in this article are not exhaustive; in fact, numerous other methods exist to enhance the performance of multipliers, such as refining the Booth algorithm, which is instrumental in generating partial products. The focus of multiplier optimization varies significantly depending on the specific applications of the microprocessor. By integrating the demands for microprocessors with varying performance characteristics within the IC industry or other industry, and subsequently analyzing and contrasting the optimization strategies for multipliers, the discourse will acquire enhanced persuasiveness and practical applicability.