1. Introduction

The The Traveling Salesman Problem (TSP) is a classic optimization problem where a salesman must visit each city exactly once and return to the starting point, minimizing the total travel distance. The problem has been a significant research topic since the 1950s. Early work, such as Mendelsohn's basic model in 1954 [1], focused on formalizing TSP using graph theory and matrix representations. In the 1960s, heuristic methods like R.L. Graham's algorithm in 1962[2] provided reasonable approximations, though not optimal solutions. The 1980s saw the development of exact algorithms like Branch and Bound and Dynamic Programming, but due to high computational costs, these were limited to small-scale instances [3].

As TSP is NP-hard, finding exact solutions for large instances is impractical, leading to a shift towards heuristic algorithms. Common methods include the Greedy Algorithm, Simulated Annealing, and Genetic Algorithms (GA). GA, in particular, has been successful due to its strong global search ability[4]. However, it struggles with local optima, affecting solution quality and convergence speed, especially for large-scale problems.

To address this, the paper proposes an improved GA that introduces a diversity-preserving mechanism. This includes an adaptive mutation strategy to enhance search ability and a dynamic tournament selection process to balance exploration and exploitation, leading to better solutions and increased population diversity.

2. Algorithm Principles and Improvement Strategies

This section first introduces the principles of the classical genetic algorithm and the improvement strategies proposed in this paper. It then provides an overview of the algorithm's implementation for solving the TSP problem.

2.1. Classical Genetic Algorithm

Genetic Algorithm is an optimization algorithm that simulates the genetic and evolutionary processes in nature. Its core idea is based on the mechanisms of natural selection, inheritance, and mutation in biological evolution. By gradually selecting superior solutions in the solution space, the genetic algorithm mimics the process where individuals better adapted to the environment are more likely to survive and reproduce, thus continuously optimizing individuals in the population to achieve the optimal solution to the problem.

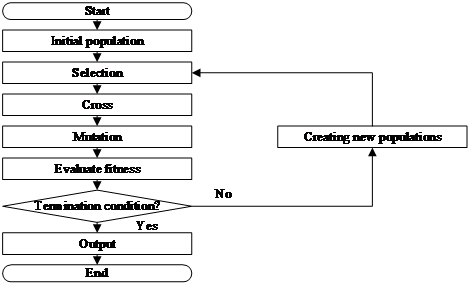
Figure 1: Flowchart of the Classical Genetic Algorithm

The basic operations of a genetic algorithm include population initialization, individual evaluation, selection, crossover, and mutation. The algorithm flowchart is shown in Figure 1.

2.2. Improvement Strategy

The classical genetic algorithm performs well in many optimization problems; however, it is susceptible to premature convergence, which can cause the algorithm to get trapped in local optima before fully exploring the solution space. To address this issue, two improvement strategies are introduced in this paper, aimed at increasing population diversity to prevent premature convergence and effectively escape local optima. The specific implementation and effects of these two strategies will be presented next.

2.2.1. Adaptive Mutation Probability Strategy

In the process of solving optimization problems using intelligent algorithms, although the algorithm can effectively explore the solution space, it may sometimes become trapped in local optima. When the algorithm enters a local optimum, the superior individuals in the population tend to concentrate around that solution, making it difficult to escape from the local optimal region. To overcome this issue, it is necessary to enhance the algorithm's exploration ability by increasing population diversity, and one common approach is to adjust the mutation strategy [6].

To address this problem, this paper proposes an adaptive mutation probability adjustment mechanism. When the algorithm detects that it has entered a local optimum, the mutation probability will be appropriately increased to enhance population diversity. Specifically, we design a local optimum detection mechanism: if the algorithm fails to generate a better solution over five consecutive generations, it is considered to have fallen into a small local optimum state. In this case, the mutation probability will be increased to twice the initial value. If no better solution is found within the next 15 generations, the mutation probability will be increased to four times the initial value. If the algorithm successfully escapes the local optimum state and finds a better solution, the current local optimum state is broken, and the mutation probability is restored to its initial value.

2.2.2. Dynamic Tournament Selection Strategy

Tournament selection is a common selection mechanism in genetic algorithms. The basic idea is to randomly select a group of individuals from the population to form a "small tournament," and then choose the individual with the best fitness as a parent [5]. However, in traditional tournament selection mechanisms, the tournament size (i.e., the number of individuals participating in the competition) is typically fixed, which may result in either excessive or insufficient selection pressure, affecting the algorithm's convergence speed and global search ability.

To address this issue, this paper proposes a dynamic tournament selection strategy that adjusts the tournament size based on the diversity of the population, thereby balancing the algorithm's ability for both global and local search. The dynamic size adjustment method is shown in equation (1).

\( {T_{dyn}}=⌊{T_{init}}×(1-\frac{g}{G})⌋\ \ \ (1) \)

Where Tdyn is the dynamically adjusted tournament size, Tinit is the initial tournament size, g is the current generation, and G is the total number of generations. This formula indicates that as the number of generations increases, the tournament size gradually decreases until it reaches a minimum value.

Specifically, in the early stages, a large tournament size means that individuals with higher fitness are more likely to be selected in each selection process [7]. This helps accelerate the propagation of high-quality solutions, allowing the population to converge to a good solution more quickly. In the later stages, as the number of iterations increases, reducing the selection pressure allows more individuals to have the opportunity to be selected, which helps maintain the diversity of the population and prevents the algorithm from getting trapped in local optima. This dynamic adjustment of the tournament size strategy can flexibly adjust the selection pressure based on the evolutionary state of the population, preventing premature convergence while maintaining sufficient exploration, thereby enhancing the algorithm's global optimization capability.

2.2.3. Improved Genetic Algorithm

The flowchart of the algorithm after introducing the improved strategies is shown in Figure 2.

Figure 2: Improved Algorithm Flowchart

2.2.4. Algorithm implementation in TSP

The improved algorithm still follows the framework of the classical genetic algorithm, with steps including population initialization, fitness evaluation, selection, crossover, and mutation. The implementation steps of the algorithm are as follows:

- Population Initialization: First, generate a number of individuals equal to the population size, with each individual representing a potential solution. During initialization, the genetic values of the individuals are generated randomly to ensure population diversity.

- Fitness Evaluation: Evaluate the fitness of each individual according to the predefined objective function. The objective function for the TSP problem in this paper is shown in Formula (2).

\( D=\sum _{i=1}^{n-1} d({P_{i}},{P_{i+1}})+d({P_{n}},{P_{1}})\ \ \ (2) \)

Where D is the total travel distance, d(Pi,Pi+1) is the distance between the i-th city and the (i+1)-th city, and n is the total number of cities. Since the TSP problem seeks to minimize the total distance, the fitness function is taken as the reciprocal, as shown in Formula (3).

\( Fitness=\frac{1}{D}\ \ \ (3) \)

Selection Operation: The dynamic tournament selection method is used to select individuals with higher fitness from the current population to enter the next generation. The dynamic size calculation formula is shown in Formula (1).

Crossover Operation: Using single-point crossover, the genes of two individuals are exchanged to generate the next generation of individuals.

Mutation Operation: To enhance the diversity of the population, certain individuals' genes are mutated randomly. To avoid falling into local optima, an adaptive mutation probability adjustment mechanism is designed. When the algorithm detects that it has entered a local optimum, the mutation probability is appropriately increased to enhance the population's diversity. Specifically, if the algorithm fails to generate a better solution within 5 consecutive generations, it is considered to have fallen into a local optimum, and the mutation probability is increased to twice its initial value. If no better solution is found within the following 15 generations, the mutation probability is further increased to four times its initial value. If the algorithm successfully escapes the local optimum and finds a better solution, the mutation probability is restored to its initial value.

- Local Optimum Judgment Mechanism: By recording the number of consecutive generations without improvement, the system determines if a local optimum has been reached. If no better solution is found within 5 consecutive generations, the mutation probability increase operation is triggered. If no better solution is found within the next 15 generations, the mutation probability is further increased until the local optimum is escaped.

3. Experimental analysis

In the experimental part of this paper, the improved genetic algorithm is compared with the classical genetic algorithm. The experimental test set is the random distribution coordinates of 20 cities in two-dimensional coordinate system (maximum value :9999). This section first introduces the parameter configuration of the experiment, and then shows the experimental results and analyzes the results.

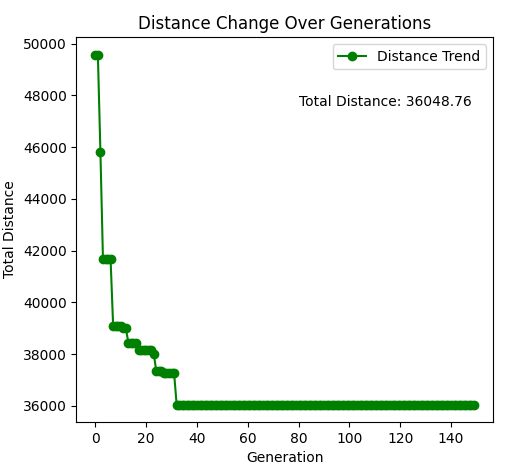
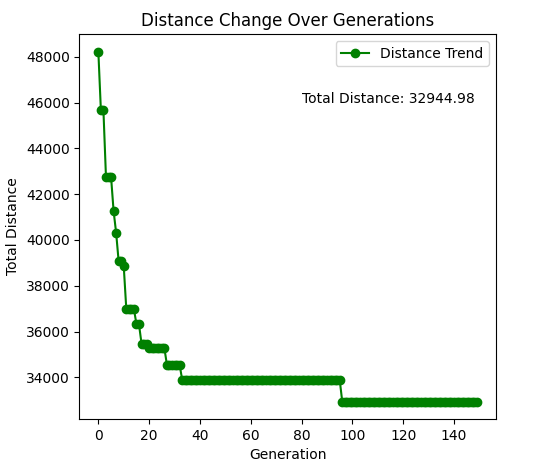
In this paper, the population of the improved genetic algorithm and the classical genetic algorithm are both 100, the maximum number of iterations is 150, the mutation probability is 0.05, and the test set is the same. On this basis, we conducted 20 independent calculations of the original classical genetic algorithm and the improved genetic algorithm in this paper respectively and recorded them. Figure 3(a) shows the best value curve after 20 calculations of the original genetic algorithm, and Figure 3(b) shows the best value curve after 20 calculations of the improved genetic algorithm.

(a) (b)

Figure 3: Comparison of algorithm operation results

The comparison of indicators after calculation is shown in Table 1.

Table 1: Comparison of algorithm operation indicators

As can be seen from Table 1, the improved genetic algorithm outperforms the classical genetic algorithm in terms of optimal solution. The optimal solution of the improved algorithm is 32944.98, which is lower than 36048.76 of the classical genetic algorithm, indicating that the improved algorithm can find a shorter path and thus has better optimization ability when solving the traveling salesman problem. In terms of average solution, the average solution of the improved genetic algorithm is 33476.57, which is also better than the 38265.23 of the classical genetic algorithm, which further proves that the quality of the solution of the improved algorithm is better in multiple runs. The results show that the improved algorithm can avoid the local optimal solution more effectively in algorithm design, and can converge stably to the better solution in the search process.

In terms of convergence speed and average running time, the classical genetic algorithm shows obvious advantages. The classical genetic algorithm can converge to the optimal solution in 42.5 generations, and the average running time is 2.23s. The improved genetic algorithm takes 108.5 generations to complete the convergence, and the average running time is 3.58s. The results show that the classical genetic algorithm can find an acceptable solution in a shorter time, while the improved genetic algorithm has slower convergence and longer running time due to the addition of diversity mechanism.

The standard deviation reflects the stability of the algorithm solution in many experiments. The standard deviation of the improved genetic algorithm is 1223.89, which is significantly lower than the 2407.48 of the classical genetic algorithm, which indicates that the improved algorithm is more stable, and can still maintain a more consistent high-quality solution after multiple independent operations.

In summary, the improved genetic algorithm has obvious advantages in the quality and stability of the solution, and performs better than the classical genetic algorithm in the aspects of optimal solution and average solution, and the improved algorithm has a smaller standard deviation, showing higher stability.

4. Conclusion

This paper reviews the development and solving methods of the Traveling Salesman Problem (TSP), highlighting the advantages and limitations of each approach. While the genetic algorithm (GA) is effective for TSP, it often suffers from premature convergence to local optima. To address this, the paper proposes an improved GA that introduces an adaptive mutation probability strategy and a dynamic tournament selection strategy, both designed to enhance population diversity and global search ability, thereby avoiding local optima. Experimental results show that the improved algorithm outperforms the classical GA in terms of solution quality, stability, and diversity, achieving shorter paths with lower variance in large-scale TSP instances. Although the improved algorithm has a slower convergence rate and longer running time, the gains in solution quality and stability make it a worthwhile trade-off.