1. Introduction

The advent of the big data era has revolutionized industries such as business, engineering, and science by significantly increasing the volume and accessibility of information [1]. While big data enhances the efficiency and availability in getting data and information, it also introduces complex challenges. These challenges stem from the sheer size, variety, and complexity of big data, making it difficult to store, analyze, and visualize such datasets for practical applications [2]. In addition, these datasets are also described by high dimensionality. Consequently, the reduction of dimensionality plays an imperative role in simplifying complex data with massive size. With origins in Pearson in 1901, principal component analysis (PCA) is one of the most renowned and traditional techniques to reduce dimensions [3]. By reducing the original variables into a smaller collection of orthogonal components, PCA reduces the dimensionality of datasets, allowing more optimal data analysis.

However, traditional PCA faces significant challenges in the context of big data. While the complexity of datasets increases in big data, high-dimensional data often leads to inefficiency because of computational complexity. The data noise can also influence PCA’s effectiveness. In addition, PCA struggles to handle dynamic data, restricting its applicability in big data environments. There is an urgent need for advanced improvements to address these challenges for big data processing. To overcome these issues, researchers have developed various advanced PCA methods, such as Incremental PCA, Sparse PCA, Kernel PCA, and Robust PCA, emphasizing the solutions of scalability, data noise, and real-world application. This paper explores these extended PCA methods and their ability to address the limitations of traditional PCA. Furthermore, it highlights PCA’s practical applications in image processing, biological data analysis, and financial modeling. Finally, the paper discusses the future directions of PCA, including using PCA with advanced machine learning technology, utilizing quantum computing to enhance efficiency, and raising privacy considerations in data analysis. Overall, this paper aims to analyze the application of PCA in big data analysis, dive into its key challenges and limitations, summarize recent improvements in order to addressing these issues, and find the improving directions in the future.

2. Mathematical Principles of PCA

Principal Component Analysis (PCA) is a dimensionality reduction technique that simplifies multivariate datasets by transforming them into a smaller set of uncorrelated variables, called principal components, while preserving as much variance as possible [4]. It identifies the orthogonal directions (principal components) where the data variance is maximized. This technique is based on the principles of linear algebra and eigenvalue decomposition. The mathematical foundation of PCA involves five key steps.

2.1. Data Centering

PCA begins by centering the data, ensuring that each feature has a mean of zero. This process removes the mean effect and standardizes the dataset, allowing the algorithm to focus on variability within the data:

X_c = X − µ(1)

where X_c is the centred data, X is the n × p matrix (with n samples, and p features), and µ is the mean vector for the features.

2.2. Covariance Matrix Calculation

The covariance matrix is calculated to captures the relationships between variables:

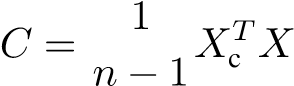(2)

Here, C is a p × p matrix representing the variance and covariance of the features.

2.3. Eigenvalue Decomposition

PCA determines the principal components by solving the eigenvalue problem for the covariance matrix. The eigenvectors represent the directions of maximum variance, while the eigenvalues indicate the amount of variance explained by each component:

Cv = λv(3)

where v are the eigenvectors (principal components), and λ are the eigenvalues, indicating the variance explained by each component.

2.4. Selecting Principal Components

Eigenvalues are ranked in descending order, and the top k eigenvectors are selected form the projection matrix W:

W = [v₁,v₂,...,v_k](4)

2.5. Projecting the Data

Finally, the original data is transformed into a lower dimensional space by projecting it onto the selected principal components:

Z = X_cW(5)

where Z is the n × k reduced representation of the data.

3. Challenges of traditional pca in big data analysis

While PCA is a widely used technique for dimensionality reduction, its application in big data environments faces several challenges. These include computational complexity in handling large-scale, high-dimensional datasets, sensitivity to noise and outliers, and limitations in dealing with dynamic or real-time data. These issues underscore the need for advanced adaptations of PCA to address the demands of big data analysis effectively.

3.1. Computational Complexity in High-Dimensional Data

One of the most significant challenges traditional PCA faces is its computational inefficiency when applied to large, high dimensional datasets. Calculating the PCA—that is, the singular vectors corresponding to several dominant singular values of the data matrix—becomes a difficult process for large and high-dimensional data [5]. For example, using PCA to analyze gene expressions with massive data size can be an extremely complex and inefficient task that consumes quantities of time. Numerous well-known issues arise with the size of features in big data, putting many traditional inferential techniques like PCA ill-posed [6]. Although PCA is an efficient method for dimensionality reduction, it still faces the issue of handling data in big data analysis.

3.2. Sensitivity to Noise and Outlier

One of the most well-known disadvantages of traditional PCA is its sensitivity to noise and outliers [7]. Data noise refers to random, irrelevant, or meaningless data that various

sources, such as measurement errors or environmental factors can cause. Since PCA computes principal components based on the variance in the data, noise can easily affect the results, leading to inaccuracy. Similarly, outliers frequently contaminate big data [8]. Outliers, which can skew the computation of the covariance matrix and eigenvectors, cause biased or misleading principal components. In the context of big data, where datasets are often massive, solving the issue of noise and outliers becomes even more significant.

3.3. Limitations to Handle Dynamic Data

Another critical limitation of traditional PCA is its inability to effectively analyze dynamic or real-time datasets. PCA is inherently designed for static datasets, which restricts its ability to adapt to changes in data over time. For instance, industrial process measurements frequently show both autocorrelation and cross-correlation. Directly applying static PCA on dynamic data can lead to several issues. It is challenging for traditional PCA to identify the connections between the measured variables since autocorrelation and cross-correlation combine because static PCA cannot identify dynamic connections from the data [9]. Big data analysis is usually dynamic, especially when dealing with real-time data; consequently, finding the measures to apply PCA into dynamic and real-time analysis is important.

4. Improvements of PCA

PCA has been extended in various ways to address its limitations in big data analysis. Extensions have been developed, including Incremental PCA, Sparse PCA, Kernel PCA, and Robust PCA. Each extension introduces unique advantages while also presenting its own challenges.

4.1. Incremental PCA

Incremental PCA (IPCA) has been extensively studied and developed to address PCA’s limitations in dynamic and real-time data environments [10]. Two primary types of IPCA exist: Candid Covariance-Free IPCA (CCIPCA) and sequential IPCA. CCIPCA allows researchers to calculate the principal components without calculating the covariance matrix [11]. IPCA allows algorithms to process dimensions sequentially, updating after each step and discarding them immediately [12]. These features make IPCA suitable for dynamic or real-time environments where data is continuously generated by reducing computational complexity and memory requirements. Both these types of IPCA enhance the efficiency and applicability in handling high-dimensional and massive data. However, it may face challenges in accuracy when data distributions shift sharply or when outliers appear.

4.2. Sparse PCA

Sparse PCA incorporates regularization techniques, such as the L1-norm or SCAD, to generate sparse principal components, improving interpretability by focusing on the most relevant features [13,14]. This method is particularly effective in handling large-size and high-dimensional data. At the same time, Sparse PCA faces the challenges like choosing the sparse parameters. The appropriate choice of sparse parameters needs cross-validation or other heuristics, while incorrect parameter selection can lead to excessively sparse. To solve this problem, one significant research topic that requires further study is named Automated Sparse PCA, which refers to a straightforward process for setting these sparse parameters [14]. Despite its advantages, Sparse PCA addresses linear relationships between variables, limiting its ability to identify non-linear structures in the data without additional improvements.

4.3. Kernel PCA

Kernel PCA can handle the non-linear distribution instead of linear features [15]. By applying the “kernel trick”, which computes relationships in the higher-dimensional space without having to compute the coordinates there, Kernel PCA maps the input data into a higher-dimensional space where linear separability may become achievable [16]. Kernel PCA can capture the non-linear connections and complex patterns through the data. Kernel PCA also provides the dimension reducing foundation for denoising fields [17]. However, Performance is significantly affected by the kernel and related hyper-parameter choices, requiring thorough consideration of the dataset and application.

4.4. Robust PCA

Robust PCA is designed to address real-world data challenges, such as noise, outliers, and missing values, which traditional PCA cannot handle effectively [18]. Two approaches to Robust PCA have been developed: one suited for lowdimensional data and is based on the eigenvectors of a robust scatter matrix, while the other is for handling high dimensional data and is based on projection pursuit, which is more suitable for the context of big data [19]. From the principles of Robust PCA aspect, this technique decomposes data into two components: a low-rank matrix that captures the hidden structure and a sparse matrix for outliers. This decomposition allows Robust PCA to separate valuable data from noise, providing more accurate results. However, robust PCA does have some limitations such as its sensitivity to parameter tuning and dependence on kernel choices.

5. Applications of PCA in big data analysis

Big data comes from different areas including images and texts. Image processing can be an important part of big data analysis, especially when handling image datasets with big sizes. Besides, big data analysis methods can be applied in biology and finance fields. Since PCA is one of the most well-known methods to reduce the dimension, it is suitable for applying this technique to image, biological, and financial areas to enhance the effectiveness when handling massive and complex datasets.

5.1. Image Processing

Image datasets, especially in fields like face recognition, are inherently high-dimensional, posing challenges in processing and analysis [20,21]. Traditional PCA, which is usually utilized in dimensionality reduction, has limitations when applied in the field like face recognition. For instance, face recognition requires transforming two-dimensional image matrices into one-dimensional image vectors. This transformation creates a high-dimensional space where accurately evaluating the covariance matrix is challenging due to its size and the limited training samples [22]. To solve these issues, some improvements of PCA are applied to the facial recognizing area, including Kernel PCA for effectively extracting features from samples with nonlinear relationships across each of their components [23], Modular PCA for separating images into smaller images known as modules to prevent feature loss along the division lines [24], matrix-based complex PCA for utilizing two matrices for displaying two distinct biometric traits of a single subject [25]. These improvements efficiently enhance the process of face recognition in the background of PCA.

5.2. Financial Data Analysis

Financial markets often generate large scale of data, such as stock prices, returns, and macroeconomic indicators, which can be highly related and noisy. PCA and its extensions is widely used in financial data analysis to reduce dimensionality and uncover hidden patterns in financial datasets. For instance, the combination of PCA and NeuroEvolution of Augmenting Topologies can create a trading signal to reach daily profits and high returns with low level of risk when investing in the financial market [26]. PCA provides financial analysis with a powerful tool to extract meaningful insights and improve decision-making by effectively handling high-dimensional and massive data.

5.3. Biological Data Analysis

In biological fields such as genomics, PCA helps visualize and summarize high-dimensional data like analyzing gene expression data [27]. However, noise and data complexity present significant challenges in biological applications. Extended PCA methods address these issues effectively. Independent Principal Component Analysis (IPCA) assumes that if most of the noise in the relevant loading vectors has been removed, biologically significant components can be recognized [28]. To address issues like noise, extended PCAs like Sparse PCA, Robust PCA, and Kernel PCA have been developed, enhancing the capabilities to handle noise, integrate heterogeneous data types, and capture non-linear patterns. Despite its challenges, PCA remains an essential method in biological research, enabling breakthroughs in analyzing complex biological systems.

6. Conclusion

In conclusion, PCA remains to be a powerful technique for dimensionality reduction in data analysis. However, traditional PCA cannot often satisfy modern data demands. It faces problems such as computational complexity, sensitivity to noise, and challenges in dynamic and real-time datasets. However, improvements such as Incremental PCA, Sparse PCA, Kernel PCA, and Robust PCA have brought new possibilities, improving scalability and efficiency, and solving the problems of noise and outliers. In the future, PCA of big data analysis methods will become more efficient and powerful with advanced technologies. For example, PCA and clustering methods in unsupervised learning, which is an algorithm in artificial intelligence and machine learning fields, can both improve and be enhanced by quantum computing technology. Artificial intelligence and machine learning algorithms can have faster training times and processing speeds via quantum computing, while quantum computers can get error correction algorithms from artificial intelligence [29]. Additionally, PCA technology in big data analysis should improve its privacy protection measures as data privacy concerns grow. By exploring its applications across other fields like image processing, finance, and biology, and connecting it with cutting-edge technologies such as machine learning and quantum computing, PCA can continue to perform as a useful tool. As researchers develop more robust and adaptive methods, PCA’s future can expand its applicability in tomorrow’s data-driven world.