1. Introduction

With the progress of science and technology, the global game industry has witnessed explosive growth, and various kinds of games have attracted a large number of players [1]. Sweepstakes are common in popular games, such as Identity Ⅴ, and are an important way for developers to attract players, increase revenue, and stay active. As players mature, market competition intensifies, and they have higher requirements for games, they hope to have a fair and reasonable lottery mechanism to get their favorite items, and optimizing the lottery mechanism has become an important issue for developers. The multi-arm slot machine model provides a new way to do this. For developers, it can help them optimize the lottery mechanism, improve player satisfaction and loyalty, achieve personalized customization, provide a more fair and reasonable experience, improve game revenue and profitability, and promote sustainable development of the industry [2]. For players, it can help them understand the principles of the lottery mechanism, improve decision-making and game skills, fair and reasonable mechanisms can increase fun and participation, and promote the healthy development of the game community. Therefore, based on the analysis of the characteristics of the lottery mechanism of " Identity Ⅴ", this paper uses the multi-arm slot machine algorithm to optimize the lottery strategy, improve the satisfaction and loyalty of players, and contribute to the sustainable development of the game.

2. Multi-arm Slot Machine Model Overview

2.1. The Principle of Multi-arm Slot Machine Model

In the multi-armed slot machine problem, multiple "arms" represent different action options. Pulling an arm produces an uncertain return [3]. The goal is to find the arm with the highest return by trying different arms for a limited time to maximize the overall return. The multi-armed slot machine serves as a decision-making tool to help participants seek the optimal path through uncertainty. Consumers need to find the best choice among many options, while considering the risk; Businesses need to pursue long-term sustainability and profitability across multiple strategies, rather than focusing solely on short-term investments. In addition, the application of multi-arm slot machines also needs to consider moral and social responsibility, not only the pursuit of maximum interests.

2.2. Multi-arm Slot Machine Model and Common Algorithms

2.2.1. Definition of the “Arms”

Suppose there are K arms, each of which produces a random return when pulled. Let Ri represent the return random variable of the i arm, whose expected return is \( {μ_{i}}=E[{R_{i}}] \) .

2.2.2. Decision-making Process

In each step t,decision maker should select one of the K arms to pull, and be rewarded accordingly. Assume \( {A_{t}} \) indicates select the arm at time step t, \( {R_{t}} \) showcases the return within time step t,which is \( {R_{t}}={R_{At}} \) . The aim to maximize cumulative return \( \sum _{t=1}^{T}{R_{t}} \) , within limited time t.

2.2.3. Common Algorithm

Greedy algorithm: Always choose the arm with the highest current expected return, which means select \( {A_{t}}=argmax{μ_{i}}(t) \) , \( {μ_{i}}(t) \) is an estimate of the expected return on the i arm up to time step t.

Thompson sampling: For each arm, random sampling is performed according to the prior distribution of its returns, and the arm with the highest sampling value is selected. Specifically, for the I-th arm, a value is sampled from the posterior distribution \( {θ_{i}} \) ,then selects \( {A_{t}}=argmax{θ_{i}}(t) \) ｡

UCB algorithm: Compute an upper confidence bound for each arm and select the arm with the highest upper confidence bound, which means select \( {A_{t}}=argmax{μ_{i}}(t)+c\sqrt[]{\frac{In t}{{n_{i}}(t)}} \) . \( {μ_{i}}(t) \) is an estimate of the expected return for i arms up to time step t, \( {n_{i}}(t) \) is the number of times the i arm is chosen, and c is a constant.

In general, the mathematical models and rules of a multi-armed slot machine revolve around making decisions in uncertain environments, maximizing cumulative returns by balancing exploration with exploitation.

2.2.4. The Use of Multi-arm Slot Machines in other Areas

In the field of Internet advertising, the multi-arm slot machine model has a wide range of applications. For example, researchers at Google have detailed in a related paper how they used a multi-armed slot machine model to optimize advertising strategies. [4]

In this case, Google is faced with the problem of displaying the most appropriate AD for each user in a large number of ads, in order to maximize the click-through rate and revenue of the AD. They see each AD space as an "arm" and different advertising strategies as different "choices." By collecting user feedback data on different ads in real time, the multi-arm slot machine algorithm is used to continuously adjust the advertising strategy, balancing the exploration of new advertising strategies and the use of known effective advertising strategies.

This application has some similarities with the application of the multi-arm slot machine model to the game lottery mechanism. In the game lottery, game developers can treat different lottery pools or lottery methods as "arms", and use the multi-arm slot machine algorithm to optimize the lottery mechanism through the players' lottery feedback data, such as adjusting the probability distribution of different rare items in each lottery pool to improve player participation and satisfaction, while maximizing the game revenue.

3. Analysis of the Lottery Mechanism of Identity Ⅴ Game (All Lottery Card Pools in the Game are the Following Probabilities)

3.1. Probability Distribution and Minimum Guarantee Mechanism

White (32%)

Green (50%)

Blue (10.2%)

Purple (2.5%)

Gold (0.5%).

Every 10 withdrawals in the same card pool must be guaranteed to produce a blue quality item

Every 60 draws in the same card pool must produce a purple quality item

Every 250 draws in the same card pool must produce one gold quality item

3.2. Analyze Players' Expectations and Satisfaction with the Results of the Game Lottery

The player usually wants to win rare, high-quality items through raffles, such as gold qualty character skins, special effects items, etc. In the field of psychology, there is a lot of research on the excitement of unexpected gains. Mihaly Csikszentmihalai, for example, mentioned that unexpected positive outcomes could bring a strong sense of pleasure and excitement when people are engaged in their favorite activities [5]. Daniel also discussed how people react to unexpected events [6]. He points out that people tend to give more attention and emotional response to unexpected outcomes, which can be positive or negative, but positive surprises usually bring pleasure and excitement. This kind of unexpected gain can break the norm and bring freshness and surprise to people, which can trigger a positive emotional responses. The book proposes the theory that unexpected positive results in engaging in favorite activities can lead to strong pleasure and excitement, analyzes the mechanism of the influence of unexpected gains in the lottery on satisfaction from the psychological root of players.

4. The Application of Multi-armed Slot Machines on Identity Ⅴ Game

4.1. Specific Methods and Steps of Applying the Multi-arm Slot Machine Model to the Lottery Mechanism of Identity Ⅴ Game

Collect a large amount of player draw history data, including the number of draws, the quality of items drawn (white, green, blue, purple, gold), the point in time of the draw, the draw pool used, etc. Analyze these data to understand the probability distribution of different items and the time law of players' lottery behavior.

Then assign value to different qualities. Gold items have the highest value, set at 100 points; Purple items are next, set to 50; Blue items are 20 points; Green items are 10 points; 5 points for white items.

4.2. Select the Appropriate Multi-arm Slot Machine Arithmetic Model

Consider using the Upper Confidence Bound (UCB) algorithm, Thompson sampling, etc. For example, UCB algorithms perform well in balancing exploration and utilization, and are suitable for making decisions in uncertain environments. Adjust the parameters of the algorithm according to the characteristics of the game and the data situation. For example, in the UCB algorithm, the exploration coefficient is adjusted to control the proportion of exploration and exploitation.

4.3. Model Application Stage

4.3.1. Initialization Phase

When introducing a multi-armed slot machine model into a game's lottery mechanism, each lottery pool (arm) is first initialized. Each lottery pool can be assigned an initial average return estimate based on historical data or prior knowledge.

4.3.2. Exploration and Application Phase

Each time a player makes a draw, a draw pool is selected according to the multi-arm slot machine algorithm. If the choice is in favor of exploration, then a lottery pool with fewer attempts can be randomly selected. If the choice is in favor of utilization, then choose the lottery pool with a higher current average return estimate. After the player draws, the average return estimate for the draw pool is updated based on the quality of the items drawn. For example, if a gold item is drawn, significantly increase the average return estimate for that lottery pool. If a white item is drawn, lower the average return estimate appropriately.

4.3.3. Dynamic Adjustment Phase

As the number of player draws increases, the parameters of the multi-arm slot machine model and the average return estimates for each draw pool are constantly updated. For example, if a lottery pool underperforms over a period of time, it can reduce the probability that it will be selected; If the newly launched lottery pool has a high attraction, the weight of its exploration can be appropriately increased. Dynamically adjust the item valuation system based on player feedback and game updates. For example, if a new character or item is introduced in the game, reassess its value and adjust the score accordingly.

4.3.4. Personalized Recommendation Stage

Use the player's individual draw history data to build a personalized multi-armed slot machine model for each player. Recommend the most suitable draw pool for players based on their preferences and historical draw behavior. For example, if a player draws blue items frequently and is satisfied with blue items, the probability of recommending blue items to that player in the lottery pool can be appropriately increased.

4.4. Effect Evaluation and Optimization

The application effect of the multi-arm slot machine model in the game lottery mechanism is regularly evaluated. The effect of the model can be evaluated by comparing player satisfaction before and after the use of the multi-arm slot machine model, the number of lottery draws, the probability of obtaining high-quality items, and other indicators. Analyze the evaluation results and find out the problems and shortcomings of the model. For example, if it is found that certain lottery pools are consistently not selected, the reason can be further analyzed, whether it is because of inaccurate return estimates or other factors.

5. Discuss How to Personalize the Drawing Strategy Based on Players' Historical Drawing Data and Behavior Patterns to Improve the Player Experience.

5.1. Analyze Historical Draw Data

By analyzing the types of items obtained from players' historical lottery data, it is possible to understand players' item preferences. For example, if a player draws and uses a particular character's skin multiple times, it can be inferred that the player has a high liking for that character. Depending on the item preference, the probability of the player's preferred item appearing in the lottery pool can be appropriately increased, or the player can be pushed a lottery opportunity related to the preferred item in a particular event.

5.2. Rules of Lucky Draw Time

Observe the timing of the lottery. Some players may participate in the draw more frequently during certain time periods, such as weekend nights. During these periods, players can be offered some additional raffle offers or increased probability of rare items to increase player engagement and satisfaction. For example, if you find that player A often draws on weekend nights, you can offer Player A a limited time discount on the draw or increase his chances of getting a high quality item during this time period.

6. The Results of the Draw after Applying the Multi-arm Slot Machine Model

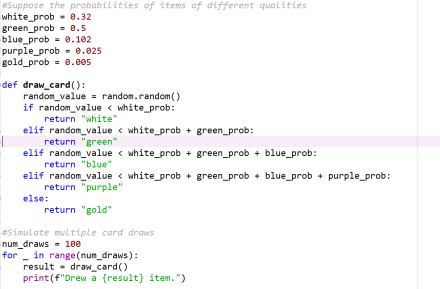
Figure 1: Python model based on multi-arm slot machine

Figure 1 The Python model that shows the results of the lottery after applying the multi-arm slot machine model, the core function is to simulate the Identity Ⅴ lottery process and present the results. It sets the probability of different quality items, such as white 0.32, green 0.5, etc., in order to build a lottery probability system. The "draw_card()" function is the key, which receives random values and determines the category of items in the draw according to the probability interval to realize the simulation of a single draw. Draws by setting the number of draws with "num_draws = 100", which is called within the loop. "draw_card()" draws and prints the results to visually display the distribution of multi-round lottery items. This model effectively evaluates the short-term performance of the model and the stability of the occurrence frequency of items, provides a key basis for optimizing the lottery strategy and adjusting the model parameters, and helps improve the players' lottery experience and game operation effectiveness. Figure 2 Showcases lottery simulation: Multi-arm slot machine Python module architecture

Figure 2: Showcases lottery simulation: Multi-arm slot machine Python module architecture

7. The Advantages of the Multi-arm Slot Machine Model in Comparison with the Traditional Lottery Mechanism

Fixed probability vs dynamically adjusted probability. In the traditional lottery system, the probability of each prize is usually fixed. For example, in a traditional Fifth Personality draw, the probability of a rare item appearing may remain at a low level, no matter how many times the player draws. This can result in players not being able to get the desired item for a long period of time, which can reduce players' enthusiasm and satisfaction.

The multi-arm slot machine model dynamically adjusts the probabilities of individual draw options based on players' historical draw data and feedback. For example, if a player does not win a desired item in multiple draws, the model can appropriately increase the probability of that item appearing in subsequent draws to increase player satisfaction. This way of dynamically adjusting probabilities can better meet the needs of players and improve the enthusiasm and loyalty of players.

8. Conclusion

The application of a multi-arm slot machine model in the lottery mechanism of the Identity Ⅴ game has achieved remarkable results. It greatly improves the gaming experience for players by dynamically adjusting lottery probabilities and personalizing recommendations. Players no longer blindly draw prizes but feel more surprised in the balance of exploration and use, and the probability of obtaining the desired items is greatly increased. At the same time, the model also brings optimization to the game operation, can adjust the strategy based on player feedback in real time, better control the in-game economic system, improve profitability, and through the analysis of player behavior develop targeted marketing strategies.

For the gaming industry, the multi-arm slot machine model brings many implications and potential applications. It provides innovative ideas for game design, integrates uncertainty and personalization into it, enhances the fun and challenge of games, and attracts more players' attention. In terms of optimizing user experience, based on the analysis of player behavior and personalized recommendations, it can better meet the needs of players, improve satisfaction and loyalty, and promote the sustainable development of the game industry.