1. Introduction

In 2008, Nakamoto originally introduced blockchain in Bitcoin: A Peer-to-Peer Electronic Cash System is a decentralized distributed ledger technology that uses a chain structure of connections to record transactions and chunk data [1]. The data of a collection of transactions is contained in each block, which is linked to the one before it by a cryptographic hash to create an unchangeable chain.

Because of its decentralization, openness, and tamperability, blockchain technology has been widely used since its introduction in a variety of industries, including supply chain management and finance. Research on blockchain-related technologies is constantly being explored, and the global blockchain industry continues to see new developments. As of December 2023, there were a total of 10,291 blockchain enterprises in the world, mainly concentrated in the United States as well as China [2]. But as blockchain applications continue to grow, the privacy protection issues brought on by these features have progressively surfaced and are now a popular area of study. The transparency of blockchain makes transaction data publicly visible, and although transactions on public blockchains such as Bitcoin are anonymous, user identities may be exposed through data analysis. In addition, the immutability of blockchain data means that sensitive information, once recorded, is difficult to delete or correct, potentially leading to privacy breaches. The public operation of smart contracts also poses privacy challenges, and participant information may be exposed in decentralized applications. Therefore, privacy protection in blockchain needs to be addressed urgently.

Chenxu Wang et al. work on the research status and outlook of blockchain data privacy protection, including four main aspects: overview of blockchain technology and data privacy protection, issues and challenges related to blockchain data privacy protection, solutions for blockchain data privacy protection, and a look at how blockchain data privacy protection technology is developing, with an emphasis on four viewpoints, such as channel isolation, information encryption, information obfuscation, and permission restriction techniques. Blockchain data privacy protection solutions are illustrated [3]. Zero-knowledge proof technology is currently achieving widespread attention in blockchain privacy protection, and the Zerocoin protocol proposed by Miers et al. utilizes zero-knowledge proof to achieve anonymous transactions, emphasizing its advantages in guaranteeing anonymity, but also exposing challenges in its implementation while demonstrating its potential in protecting the privacy of user identities [4]. In addition, homomorphic encryption technology is also considered one of the important means to improve blockchain privacy protection, and Gentry established the groundwork for further study and applications in the area of blockchain privacy protection by putting forth the first comprehensive homomorphic encryption algorithm in 2009 [5].

The primary topics covered in this article are blockchain privacy risks, blockchain privacy protection technology, and the technology's prospects for the future. Following an introduction to the conventional blockchain architecture in the section on privacy threats, the paper examines the privacy risks posed by the four layers of the blockchain: the data layer, network layer, transaction layer, and application layer. Additionally, the blockchain privacy protection technology covers the homomorphic encryption and zero-knowledge proof of the two key blockchain chain privacy protection strategies.

2. Blockchain Privacy Threats

2.1. Blockchain Architecture

As seen in Figure 1, prior research often separates the blockchain architecture into data, network, consensus, incentive, contract, and application layers.

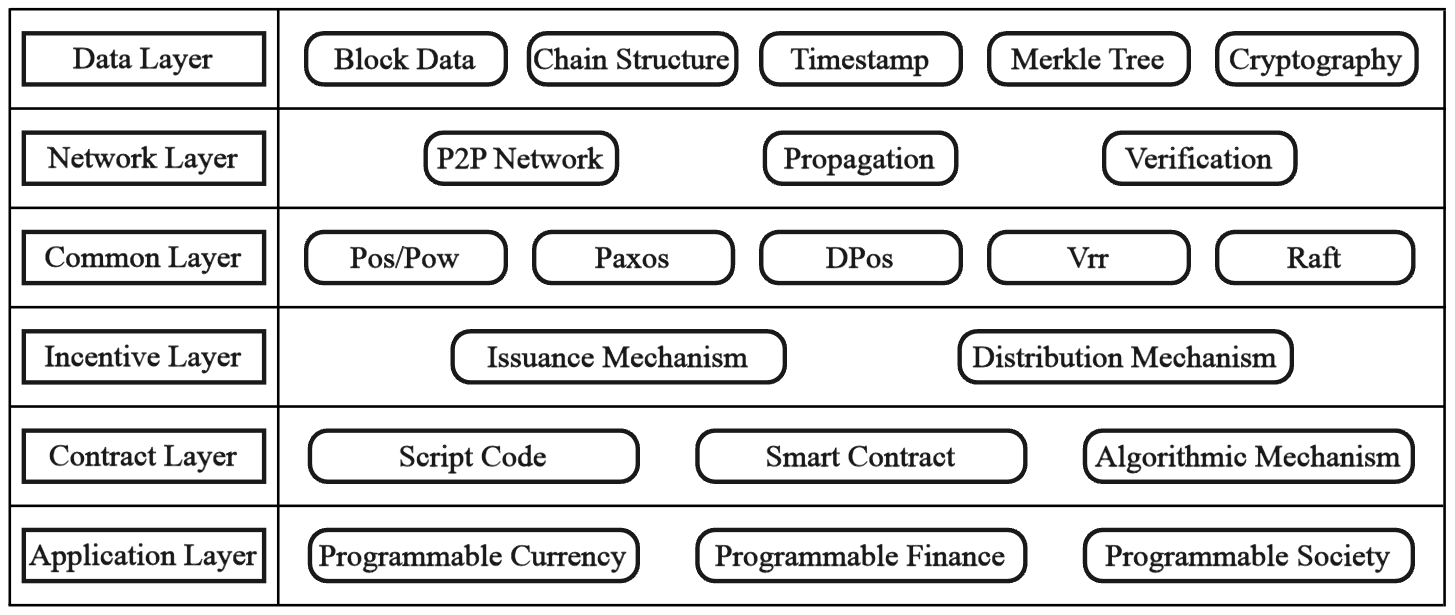
Figure 1: Blockchain System Architecture Diagram [6].

However, as blockchain technology advances and is updated frequently, its architecture is also modified and optimized continuously. For instance, based on the features of blockchain technology, Zhu Liehuang et al. divide the privacy protection mechanism in blockchain into three groups [7]: network layer privacy protection, transaction layer privacy protection, and application layer privacy protection. Tan Pengliu et al. divide the blockchain's privacy protection mechanisms into four groups: cryptography, privacy protocols, obfuscation technology, and decentralized identity authentication [8]. The four layers of the blockchain architecture are the data layer, network layer, transaction layer, and application layer, according to reference [4] in this study.

2.2. Privacy Threat

In blockchain technology, privacy threat is a very important but more complicated one, and the privacy threats existing in blockchain are summarized from the following four categories with reference to the classification of blockchain architecture in the previous section.

2.2.1. Data Layer Privacy Threats

The data layer of the blockchain system stores transaction information of different users, including information about the transaction's initiator, recipient, and amount. Because of the blockchain's unique data structure and access control mechanism, the storage and access of this data may be vulnerable to privacy leaks.

(1) Storage security problem: The decentralization and non-tamperability of blockchain relies on the backup of data by all nodes. As the amount of data grows, the storage burden on nodes increases, which may result in some nodes being unable to store complete historical data. In that case, malicious nodes may access or tamper with the data through attacks, jeopardizing the privacy and security of transaction records.

(2) Access security problem: In blockchain, data access control requires accurate identification of visitors. The current centralized PKI faces many security problems [9,10], such as CA being attacked, untrustworthy and single point of failure. Meanwhile, the vulnerability of access control may be exploited by malicious visitors to realize the overstepping access and threaten the privacy of transaction records.

2.2.2. Network Layer Privacy Threats

Due to the public nature of the blockchain network, any node can access the network layer, making it possible for malicious nodes to obtain some private information by listening to the network communication.

(1) Node information privacy: malicious nodes can listen to and analyze network communications to obtain information such as IP address, adjacency, and server location of nodes, which may be used for further analysis and attacks, jeopardizing the privacy and security of nodes.

(2) Communication data privacy: the content of communication between nodes, including the plaintext data, traffic and time of communication, may be captured and analyzed by malicious nodes, and the leakage of this information may be used to infer the identity of the initiator of the transaction, threatening the privacy of communication data.

2.2.3. Transaction Layer Privacy Threats

Transaction information located on the blockchain is transparent to all participating nodes, which may result in the following two types of privacy breaches:

(1) User identity privacy: the user's real identity information, such as identity card number, telephone number and residential address, may be inferred by analyzing the relationship between the transaction network and the user's network.

(2) Account address privacy: The account address and its balance, transaction history and other information involved in the transaction records are also at risk of privacy leakage, and the attacker can correlate the user's real identity by analyzing the transaction pattern and change address.

2.2.4. Application Layer Privacy Threats

Blockchain poses the following privacy risks while providing interfaces and services to users at the application layer:

(1) Client privacy: When using the application, users may leak sensitive information such as account addresses and keys due to low security awareness or the use of insecure software.

(2) Service Provider Privacy: In the course of providing application services, service providers may leak private user information due to insecure protocols or improper internal operations.

3. Blockchain Privacy Protection Technology

3.1. Homomorphic Encryption

3.1.1. Fundamentals of Homomorphic Encryption

A unique kind of encryption called homomorphic encryption enables arithmetic operations to be carried out directly on the ciphertext without the need for previous decoding. The main goal is to use a certain mathematical architecture to ensure that the outcome of the computation that was decrypted is consistent with the outcome of carrying out the same operation on the plaintext [5]. In case the encrypted data is not decrypted, the data can still be processed and manipulated, thus protecting the privacy of the data.

If some operation \( ⨁ \) is performed on the ciphertext \( {C_{1}} \) and \( {C_{2}} \) , the decryption result \( D({C_{1}}⨁{C_{2}}) \) is equivalent to performing the operation on the plaintext \( {m_{1}}∘{m_{2}} \) , i.e \( D(E({m_{1}})⨁E({m_{2}}))={m_{1}}∘{m_{2}} \) .

There are two primary categories of homomorphic encryption based on the computation types that are supported: A single operation type, such addition or multiplication, is supported by partial homomorphic encryption (PHE); arbitrary operations, including addition and multiplication, are supported by fully homomorphic encryption (FHE).

3.1.2. Application Scenarios of Homomorphic Encryption in Blockchain

Blockchain is known for its decentralized and tamper-proof nature, but its public ledger nature makes user privacy easily exposed. Protecting data privacy is particularly important in areas such as finance, healthcare, and the Internet of Things [1]. Therefore, it is especially necessary to introduce co-located encryption to solve these problems.

(1) Data privacy protection: figure 2 shows a reference implementation of full homomorphic encryption for data privacy protection computation [8], with homomorphic encryption, users can conduct transactions without revealing data. For example, in the medical field, patients' health data can be encrypted and stored on the blockchain, and healthcare organizations can analyze and research without decrypting the data [11].

Figure 2: Reference implementation of full homomorphic encryption for data privacy preserving computations [8].

(2) Secure execution of smart contracts: same-stage encryption can enhance the privacy of smart contracts. In traditional smart contracts, all participants can see the details of contract execution. With same-stage encryption, these details can be encrypted and decrypted only when specific conditions are met [12].

(3) Data sharing and collaboration: In multi-party data collaboration, same-site encryption allows parties to perform computations without sharing the original data. This is especially important for scenarios that require cross-organizational collaboration while protecting the privacy of their respective data.

3.1.3. Performance and Security Analysis of Homomorphic Encryption

The performance of homomorphic encryption is usually limited by the computational complexity and the size of encrypted ciphertexts, and the computational complexity of FHE is high, which is mainly reflected in the three aspects of encryption, decryption, and ciphertext operations. Current mainstream FHE implementations such as BGV [13], CKKS [14] and other schemes have significant improvement in computational efficiency, but still face great challenges in practical applications, for example, 1) computational efficiency: FHE implementations usually need to deal with operations on polynomial rings resulting in high computational complexity, and Gentry's scheme for example, which uses heavy computational resources to support ciphertext multiplication and multiplication operations [5]. operations [5], recent optimization strategies based on Number Theoretic Transform (NTT) and more efficient coding strategies (e.g., Double-CRT representation [15]) have significantly improved the efficiency; 2) Storage and communication costs: ciphertexts are usually many times larger than plaintexts, which puts a higher demand on storage and communication resources. which puts higher demands on storage and communication resources.

Homomorphic encryption security is typically built on challenging mathematical problems, such the Learning With Errors (LWE) problem or the huge integer decomposition problem [16]. Current research focuses on whether these issues are still secure in the age of quantum computing. 1) Security model: the security of FHE systems is typically predicated on intricate mathematical presumptions, such as the LWE problem, while the security model of homomorphic encryption typically incorporates semantic security and resistance to chosen-plaintext assaults [16]. 2) Impact of quantum computation: There has already been discussion about how quantum computers could undermine established public-key cryptography regimes. Homomorphic encryption schemes based on the LWE problem are thought to be more resilient to quantum attacks [16], but encryption schemes based on integer factorization and discrete logarithm problems are threatened by Shor's algorithm, which can solve these problems in polynomial time [17].

3.2. Zero-Knowledge Proof

3.2.1. Basic Concepts of Zero-Knowledge Proofs

In 1985, Goldwasser, Micali, and Rackoff introduced the zero-knowledge proving technique [18], and its core example, Figure 3, is that there exists a statement that can be tested for correctness through specific steps, and the prover, without revealing any information about the evidence associated with the statement, causes the verifier to believe that the statement made by the Prover is correct.

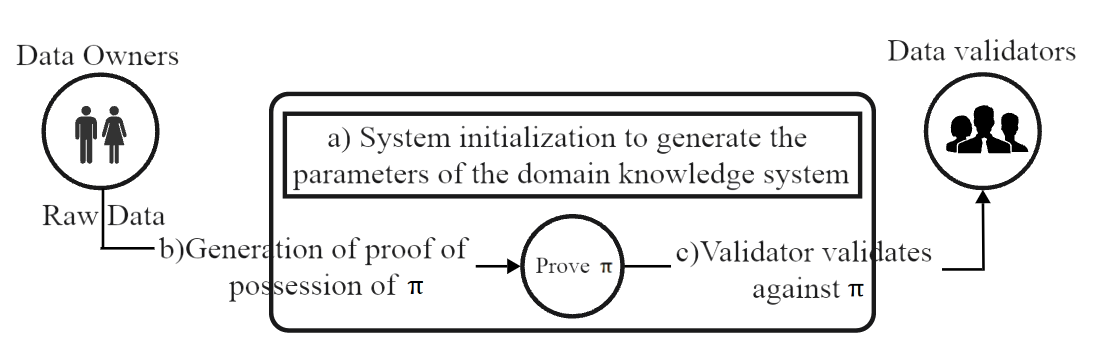
Figure 3: Zero-knowledge proof data privacy protection model diagram [8].

A zero-knowledge proof must satisfy the following three properties [9]:

(1) Completeness, if the statement is indeed correct, the honest prover (P) is able to convince the verifier (V) of the truth of the statement.

(2) Reliability (Soundness): Any dishonest prover will be unable to persuade the verifier to accept the statement if it is untrue.

(3) Zero-Knowledge: The entire proof process may lead the verifier to conclude that the statement is true, but it will not reveal to them any further knowledge beyond the statement's accuracy.

Regarding whether the proof process necessitates multiple information exchanges between the prover and the verifier, zero-knowledge proofs can be divided into two categories [8]: 1) Interactive Zero-Knowledge Proofs (IZK), which require multiple information exchanges between the prover and the verifier, and 2) Non-Interactive Zero-Knowledge Proofs (NIZK), which only require the prover to send a single proof message and do not necessitate multiple information exchanges between the prover and the verifier. With Interactive Zero-Knowledge Proofs (NIZK), the prover simply needs to transmit a single proof message to the verifier, eliminating the need for several information exchanges. However, interactive zero-knowledge proofs have some limitations. That is, they can only be used outside of the proof process to convince the third party that the proof process is correct, and they cannot be used to prove the correctness of the proof process to anyone other than the prover and the verifier. Non-Interactive Zero-Knowledge Proofs overcome these limitations.

3.2.2. Zero-Knowledge Proofs in Blockchain

Zero-knowledge proofs are widely used in this area of blockchain in several ways, such as privacy protection and transaction anonymity, scalability and performance optimization, decentralized authentication and authorization, smart contracts and data privacy, and cross-chain interoperability.

(1) Privacy protection and transaction anonymity: transactions on the blockchain are generally publicly visible, i.e., anyone can view all transaction information, and zero-knowledge proof can verify the legitimacy of the transaction without revealing the specific content of the transaction, which can, to a certain extent, satisfy the needs of users who wish to hide certain sensitive information. zCash is a successful example of the anonymity of transactions achieved by using zk-SNARKs technology. ZCash is a successful example of using zk-SNARKs to anonymize transactions, allowing users to selectively hide the sender, receiver, and amount of the transaction.

(2) Scalability and performance optimization: as the quantity of transactions rises, the performance of the network will be affected to varying degrees, and this problem is the scalability of the blockchain. Zero-knowledge proof by compressing a large amount of transaction data into a small proof uploaded to the blockchain, by virtue of this way to significantly slow down the chain in the storage requirements and thus make the efficiency of the network can be improved. Zk-Rollups is a kind of application program, which compresses a large number of transactions into a zk-SNARK proof, which significantly improves the transaction throughput of the ethereum.

(3) Decentralized authentication and authorization: in some decentralized identity management systems, users prove that they have certain qualifications through zero-knowledge proofs without having to disclose private information. In Sovrin network, for example, users can use zk-SNARKs to verify their credentials and prove their identity.

(4) Smart Contracts and Data Privacy: Smart contracts are usually publicly visible, but in some scenarios where confidentiality is required, zero-knowledge proofs can be used to prove that the execution result of a smart contract is eligible without exposing the actual data.Secret Network utilizes the zk-SNARKs technology to ensure the privacy of the input and output data of a smart contract.

(5) Cross-chain interoperability: Users can verify ownership or transfer between different blockchains through zero-knowledge proofs without revealing specific asset details anymore. In the case of Polkadot, for example, the validity of cross-chain asset transfers is verified through zk-SNARKs without revealing specific asset details.

3.2.3. Technical Challenges of Zero-Knowledge Proofs

Despite their many blockchain uses, zero-knowledge proofs continue to confront associated technological difficulties.

(1) Computational and storage overhead: the generation of zero-knowledge proofs and the verification process require high computational resources, especially in some more complex proofs, such as zk-SNARKs.

(2) Standardization and compatibility issues: different zero-knowledge proof schemes have certain differences in details, and specific solutions to ensure interoperability between different blockchains and applications still require further research, thus standardization of zero-knowledge proof and cross-chain compatibility is a major challenge existing in the current zero-knowledge proof technology.

(3) Trusted setup problem: In some specific cases some protocols (e.g., zk-SNARKs, etc.) require a trusted setup phase, which, if not properly handled, may lead to security problems in the system.

4. Conclusion

This paper analyzes the privacy threats in blockchain from the architecture of blockchain at four levels, and then specifically focus on two major blockchain privacy protection technologies, homomorphic encryption and zero-knowledge proofs, which are divided into the basic concepts, applications in blockchain, and challenges faced nowadays.

Homomorphic encryption and zero-knowledge proofs have played a key role in the technological development of blockchain privacy protection. In the future, homomorphic encryption is expected to make advances in computational efficiency and expand its application scope, while zero-knowledge proofs will continue to increase verification speed and reduce computational complexity. Furthermore, integrating these two technologies could result in a more comprehensive privacy protection plan that not only satisfies user privacy requirements but also advances the adoption of blockchain technology across numerous industries.