1. Introduction

1.1. Background

Microorganisms face unique challenges when swimming in low Reynolds number environments. The Reynolds number is the ratio between inertial and viscous forces. Because inertial forces are negligible in an environment with a low Reynolds number, viscous forces dominate their movement [1]. Unlike the human swimming mechanism, which employs body mass and inertia, microorganisms must adopt specific strategies to move through highly viscous environments effectively. Flagellar rotation and fluid interactions are essential for propulsion in such an environment.

Except for viscosity, the structure of surroundings also plays a role in determining the swimming efficiency of microorganisms. Study has shown that unbranched polymers, such as methylcellulose, create a structured network that promotes flagellar propulsion. Microorganisms adopt a corkscrew-like motion in these structured viscous solutions to penetrate efficiently. Therefore, helical bacteria, like Leptospira, exhibit remarkable adaptations when they swim in viscous environments [2].

When microorganisms move through soil, their behavior also provides deeper insights into locomotion in viscous surroundings [3]. Like low Reynolds number environments, soil also presents a complex matrix. In the soil, microbial movement is influenced by factors including soil texture, pore size, and water content. Microorganisms rely on advection and hydrodynamic dispersion to move through soil. Additionally, preferential flow paths, such as macropores and fractures, play a crucial role in microbial movement. They enable certain bacteria to migrate more rapidly. This phenomenon in soil studies highlights how structured environmental pathways can significantly increase the efficiency of microbial transport.

1.2. Study Objective

This study discusses how microorganisms adapt their swimming mechanisms to environments with low Reynolds numbers. The focus is achieved by analyzing theoretical concepts, building computational simulations, and conducting physical experiments. The study is developed based on insights from critical studies, including Purcell’s foundational work on viscosity and Lauga’s hydrodynamic principles. This paper aims to explain the relationships between viscosity, flagellar movement, and swimming efficiency. Overall, the study’s primary objective is to investigate how varying fluid viscosities influence propulsion in microbial locomotion. This goal will provide new perspectives for advancing research in microbiology and bioengineering.

1.3. Literature Review

1.3.1. “Life at Low Reynolds Number.”

This document explains the concept of low Reynolds numbers and discusses the unique challenges microorganisms face when they swim in viscous environments. In such an environment, viscous forces dominate over inertial forces. This phenomenon creates ineffective momentum-based propulsion. Purcell points out the scallop theorem. It explains why reciprocal movements, such as simple back-and-forth motions, cannot produce net movement in low Reynolds number fluid. Microorganisms have developed non-reciprocal movements, like rotating helical flagella [1]. This mechanism propels them forward effectively through the fluid. This principle is essential for understanding the swimming mechanisms of microorganisms in low Reynolds number environments.

1.3.2. “The Hydrodynamics of Swimming Microorganisms.”

Building on Purcell’s principles, Lauga and Powers further explain how flagella are essential motility structures for microorganisms. The flagella can function as rotary motors that generate propulsion through continuous rotation. Their study reveals a relationship between the swimming speed of microorganisms and the rotation distance of the flagella: at low swimming speeds, the rotation distance remains nearly constant; however, at higher swimming speeds, the rotation distance begins to decrease linearly [4]. This interaction plays a critical role in understanding how microorganisms achieve efficient movement. This mechanism can enhance swimming stability in high-viscosity environments by minimizing erratic movements. Although rotational speed may decrease when erratic movements are declined, the more stable interaction between flagella and fluid can improve propulsion efficiency. This vital theory forms an essential basis for the experiment.

1.3.3. “A Mathematical Explanation of an Increase in Bacterial Swimming Speed with Viscosity in Linear-Polymer Solutions.”

The document examines the swimming behavior of microorganisms in polymer solutions. The research in the article demonstrates the positive relationship between the swimming speed of microorganisms and the concentration of the solution. It introduces normal and tangential viscosities to explain this phenomenon. Most importantly, it provides step-by-step formulas to calculate the swimming speed of microorganisms under various conditions. Key variables include the flagella’s length, rotation speed and distance, the microorganism’s size, and the surrounding environment’s viscosity [5].

The calculation method involves determining the α and γ drag coefficients of the flagellar filament as well as the α drag coefficient of the cell. The swimming speed is determined by multiplying the flagellar filament's γ drag coefficient by the rotation frequency and then dividing by the sum of α drag coefficients of the aflagellar filament and the cell.

I translated this method into MATLAB code to simulate the impact of different pitch angles on swimming speed. The results shown in Figure 1 demonstrate that the speed increases when the pitch angle is below 45 degrees. However, according to the results, the swimming speed decreases once the angle exceeds 45 degrees. This finding helps us understand microorganisms’ swimming mechanisms and enables practical applications.

Overall, the author’s work offers critical insights into resistive force theory for experiment, which relates tail rotation to propulsion force. This theory explains the way fluid viscosity affects swimming speed.

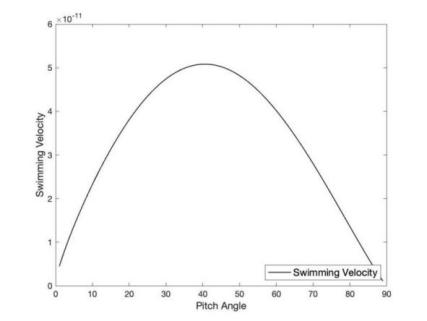
Figure 1: The Plot of Swimming Velocity under Different Pitch Angles, via MATLAB.

2. Experiment

2.1. Introduction

The experiment is conducted based on the fluid mechanics of microorganisms. Microorganisms propel themselves forward in the fluid by rotating their flagella. The experiment aims to simulate flagellar propulsion. It also explores the effect of different tail rotation rates on swimming speed in two environments with varying viscosities. The goal is to understand how fluid viscosity impacts propulsion efficiency while simultaneously assessing whether the model’s behavior aligns with natural microorganisms’ motion. Additionally, the results provide meaningful insight into designing biomimetic propulsion systems.

The experiment consists of a physical model and two testing environments: water without and water with detergent. The model mimics a microorganism’s shape and function. It comprises four main parts: a main body, an afterbody (with two vertical holes at each end), a connector (which links the body and the afterbody), and a tail. The body, connector, and afterbody are designed in SOLIDWORKS and manufactured with 3D printing. The wire constructs the tail.

I choose SOLIDWORKS to design the model components because of its excellent ability to create complex shapes accurately. On SOLIDWORKS, I can optimize the model’s geometry for smooth, fluid interaction. This software also enables me to get precise control over dimensions. I use a 3D printer to manufacture the components with nylon material for its lightweight and durable properties. The wire tail provides the flexibility to replicate flagellar movement.

In Figure 2 and 3, the main body and afterbody are cylindrical, mimicking the streamlined shapes of microorganisms. The cylindrical structure helps reduce the influence of the fluid drag. The afterbody contains two vertical holes, each passing the rubber band and attaching the tail.

Figure 2: Main Body, via SOLIDWORKS.

Figure 3:Afterbody, via SOLIDWORKS.

The connector shown in Figure 4 has a central hole to align with the cylindrical component inside the main body. This feature guarantees the stability of the connection between two components. Another vertical hole allows the rubber band to pass through to connect with the afterbody. This configuration facilitates the smooth transfer of elastic energy from the twisted rubber band to the rotating tail.

Figure 4: Connector, via SOLIDWORKS.

Microorganisms rotate their flagella to push against the surrounding fluid, generating forward motion. The model replicates this moving mechanism with a rubber band, as shown in Figure 5. One end of the band is anchored inside the main body, while the other end is twisted via the afterbody to store elastic energy. Upon release, the rubber band unwinds to drive the tail’s rotation and propel the model forward.

Figure 5: Actual Model, via 3-D Printing.

2.2. Procedure

The experiment was conducted in two different fluid environments: water without detergent (low viscosity) and water with detergent (higher viscosity). Each trial follows the same Procedure to avoid the influence of any other factors:

Twisting the rubber band: The afterbody was twisted 10 times by hand to store consistent elastic energy.

Placing the model: The model was carefully placed in the testing liquid.

Releasing the model: Once released, the rubber band unwound to rotate the tail and propel the model forward through the fluid. This process is shown in Figure 6.

Figure 6: Releasing the Model.

2.3. Measurement Method

The swimming distance was a straight-line distance from the model’s starting points to its ending positions in the fluid. After the model finished its motion, a ruler measured the distance between the starting and final points to provide an accurate estimation.

A mobile phone was used to record a video of the model’s motion from start to finish. The video was later analyzed to determine the exact time duration by noting the timestamps at the start and end of the motion.

The tail rotation rate was also determined through the recorded video. The video was played back in slow motion, allowing the observer to count the rotations of the tail tip.

2.4. Result and Data Analysis

The results from both environments were ranked based on swimming speed, as shown in Figure 7 and 8. The trials were divided into three groups for each environment: highest, middle, and lowest speeds. The average values from these groups were used to generate two line graphs illustrating the relationship between rotation speed and swimming speed.

Swimming speed is equal to swimming distance (measured with a ruler) divided by time (obtained from video analysis).

Tail rotation rate is equal to total rotations (counted from slow-motion video playback) divided by time (determined from the video).

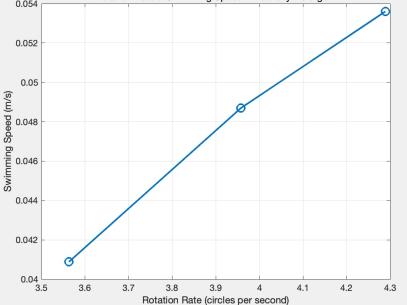
Figure 7: Relationship between Rotation Rate and Swimming Speed in Water, via MATLAB.

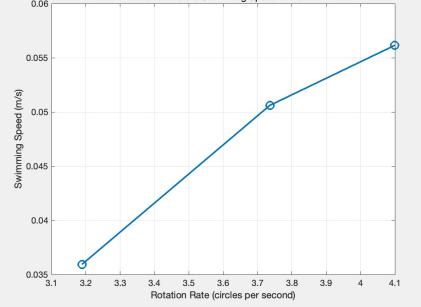
Figure 8: Relationship between Rotation Rate and Swimming Speed in Laundry Detergent, via MATLAB.

2.5. Result Discussion

The results in Figure 7 and 8 reveal a positive correlation between tail rotation rate and swimming speed. Key observations include:

The model encountered more resistance in the high-viscosity detergent water, resulting in a shorter travel distance. However, this did not negatively impact swimming speed because the higher resistance reduced the rubber band's unwinding time, balancing the propulsion speed.

The detergent water’s rotation rate was more stable, with more minor variations between trials. This is likely due to the higher viscosity stabilizing the tail’s rotation.

The results aligned with Magariyama and Kudo’s finding that higher viscosity can improve propulsion efficiency by reducing erratic movements. They also supported Lauga and Powers’ predictions that resistive force theory explains the relationship between fluid resistance and optimized propulsion.

2.6. Limitation and Error Analysis

Potential sources of error included inconsistent rubber band twisting and small fluctuations in water temperature. These differences could slightly affect the fluid’s viscosity.

2.7. Experiment Conclusion

This experiment successfully mimics the propulsion mechanism of microorganisms through a simplified model. The rotation of a wire tail drives the model, which is powered by a twisted rubber band. The results demonstrate that the tail rotation rate and fluid viscosity are crucial in determining swimming speed. Fluids with higher viscosity can better support stable rotational behavior. Such fluid may also increase resistance, leading to shorter moving distances. However, the increased resistance shortens the swimming duration, keeping the overall speed consistent.

Using two fluid environments with different viscosities creates a meaningful comparison, shedding light on the connection between viscous resistance and rotational propulsion. The experiment highlights the importance of understanding fluid-structure interactions. The interaction between microorganisms and fluid is fundamental for further studies about microbial locomotion and biomimetic propulsion systems.

3. Discussion

The MATLAB simulation results further confirm Magariyama and Kudo's findings. They demonstrate that swimming speed increases with viscosity until it reaches a critical threshold and then declines. The experiment results highlight the importance of interactions between fluid viscosity and microorganisms’ swimming behaviors. As viscosity increases, rotational stability improves. However, the swimming distance decreases during the process. This trade-off between stability and speed highlights the complexity of microbial locomotion and offers valuable insights for designing biomimetic systems. These findings align closely with prior research. They support the view that viscosity plays a dual role in microbial propulsion by stabilizing movement while limiting speed.

4. Conclusion

This study offers new insights into the fluid dynamics of microswimmers in low Reynolds number environments. Both computational simulations and physical experiments confirm that viscosity is critical in determining swimming efficiency and stability. The findings suggest that controlling the pitch angle below 45 degrees can optimize swimming speed. The results indicate higher viscosities stabilize rotational movement at the expense of distance traveled.

The experiments validate the theoretical foundations provided by Purcell, Lauga, and Magariyama, demonstrating the importance of non-reciprocal movements in microbial locomotion. These insights are valuable for advancing our understanding of microbial behavior. They can have practical applications in developing biomimetic propulsion systems. Future research can explore the behavior of microorganisms in more complex fluid environments to further enhance the design of artificial microswimmers. They will promote advancements in related fields such as microbiology and bioengineering.