1. Introduction

In modern electrical systems, by conducting accurate electrical load forecasting analysis, the costs of the power system can be effectively reduced [1]. With the modern power industry transitioning towards different systems and functions, an increasing number of decision-making processes are beginning to rely on the analysis of load uncertainties [2]. If there are deviations in load forecasting, it may lead to an unreasonable power generation plan, resulting in a shortage or surplus of power supply. In severe cases, it may even threaten the stability of the power grid and affect the reliable operation of the electrical system.

At present, there are a wide variety of load forecasting methods, covering many fields such as physical methods, statistical methods and artificial intelligence methods [3]. The literature [4] adopts stepwise regression analysis to strongly screen the characteristic quantities for power load forecasting, and establishes a blind number regression model to make the accuracy of electrical load forecasting improved. The literature [5] adopted the short-term SVM electrical load forecasting method ground on K-Means clustering and achieved the research on the influence of temperature and holidays on seasonal loads. The literature [6] adopted the exponential smoothing method and solved the difficult problems such as large time span and wide geographical distribution in medium-long term electrical load forecasting. The literature [7] adopted a short-term electrical load forecasting model ground on the deep residual network and achieved the integration of domain knowledge and researchers' comprehension of the task through various neural network building blocks. The literature [8] adopts the method of ultra-short-term power load forecasting based on the improved Q-learning algorithm and combined model, and its forecasting accuracy reaches more than 98%. The literature [9] employs the Firefly algorithm. By screening out multiple highly efficient learners for integration, it effectively improves the prediction accuracy.

However, traditional physical methods and statistical methods have certain limitations. Physical methods rely on precise physical models and a large number of system parameters. The modeling process is complex and has poor adaptability to changes in actual operating conditions. When addressing nonlinear and non-stationary data, statistical methods perform poorly. And it is difficult for them to accurately capture the complex variation laws of load data. In comparison, artificial intelligence methods have powerful self-learning and self-adaptive abilities. They can handle complex nonlinear relationships, have outstanding capabilities in feature extraction and pattern recognition of large-scale data, and possess strong generalization abilities. Therefore, they are widely applied.

This paper adopts the hyperparameter load forecasting method ground on the Long Short-Term Memory Network (LSTM) optimized by Quantum Particle Swarm Optimization (QPSO). Firstly, the collected power load data and related meteorological data are preprocessed. Through data processing steps such as normalization, effective load influencing features are extracted. Secondly, an LSTM network model is constructed. Utilizing its ability to handle the permanent and temporary dependency relationships of time series data, load forecasting is carried out. And the hyperparameters of the LSTM model is optimized by the QPSO algorithm to improve the prediction accuracy and generalization ability of the model. Finally, through case analysis, comparing with the conventional LSTM model and other artificial intelligence methods, the superiority and effectiveness of the proposed method in load forecasting will be verified.

2. The prediction model ground on the Long Short-Term Memory Network optimized by Quantum Particle Swarm Optimization

2.1. Problem description

In today's complex and changeable energy environment, the stable operation of power systems and optimizing energy allocation depends on accurate power load forecasting. Power load data is affected by numerous factors and exhibits highly nonlinear and non-stationary characteristics.

When conducting LSTM load forecasting based on QPSO, data preprocessing is a crucial initial step. The original power load data and related influencing factor data (such as meteorological data, date types, etc.) often have problems such as noise, missing values, and outliers, which will have an adverse impact on subsequent model training and prediction results.

For missing values in the data, we use the linear interpolation method for filling, which can estimate the missing values according to the data points before and after the missing values through a linear relationship, which can, to a certain extent, preserve the original trend of the data. For noisy data, we use the moving average filtering method for processing, which can smooth the data and reduce the interference of noise by calculating the average value of the data within a certain window in the data sequence.

After the data cleaning is completed, in order to make different types of data comparable, we perform normalization on the data. In order to map the data into the interval [0, 1], the Min - Max normalization method is adopted, which can preserve the characteristics of the original distribution of the data and help improve the training efficiency and rate of convergence of the model.

In this study, we choose to use the LSTM network for load forecasting. LSTM is a special sort of recurrent neural network (RNN). By introducing the gating mechanism, the problems of gradient explosion and gradient vanishing that occur when the traditional Recurrent Neural Network (RNN) processes long-sequence data have also been effectively solved. LSTM can remember long-term historical information and make predictions based on the current input and historical information, making it very suitable for predicting power load data with time series characteristics.

2.2. Methodology

2.2.1. The algorithm based on quantum particle swarm optimization (QPSO)

The algorithm based on Quantum Particle Swarm Optimization is developed on the basis of the traditional algorithm based on Particle Swarm Optimization (PSO). In PSO, each potential solution is represented by a particle, and based on its own historical best position and the historical best position of the group, the particle can move effectively in the search space. While QPSO introduces the concept of quantum mechanics and regards the movement of particles as the evolution of quantum states.

In QPSO, the position update formula for each particle is:

\( {x_{i}}(t+1)={ϕ_{i}}(t)\cdot {p_{i}}(t)+(1-{ϕ_{i}}(t))\cdot {P_{g}}(t)±α\cdot |mbest(t)-{x_{i}}(t)|\cdot ln{(\frac{1}{{u_{i}}(t)})}\ \ \ （1） \)

Among them, the position of the i-th particle in the t-th generation is denoted by \( {x_{i}}(t) \) , where \( {ϕ_{i}}(t) \) is a random number, the historical best position of the i-th particle and the historical best position of the group are denoted by \( {p_{i}}(t) \) and \( {P_{g}}(t) \) respectively, \( α \) is called the contraction - expansion coefficient, the average value of the historical best positions of all particles is denoted by \( mbest(t) \) , and \( {u_{i}}(t) \) is a random number defined in the interval [0,1].

2.2.2. Long short-term memory network (LSTM)

The basic components of an LSTM (Long Short - Term Memory) network are the input gate, the forget gate, the output gate, and the memory cell. How much of the current input information can enter the memory cell is determined by the input gate; which information in the memory cell needs to be forgotten is determined by the forget gate; how much of the information in the memory cell can be output is determined by the output gate.

The core calculation formulas of LSTM are as follows:

Forget gate:

\( {f_{t}}=σ({W_{f}}[{h_{t-1}},{x_{t}}]+{b_{f}})\ \ \ （2） \)

Input gate:

\( {i_{t}}=σ({W_{i}}[{h_{t-1}},{x_{t}}]+{b_{i}})\ \ \ （3） \)

Candidate Memory Cell:

\( \widetilde{{C_{t}}}=tanh{({W_{C}}[{h_{t-1}},{x_{t}}]+{b_{C}})}\ \ \ （4） \)

Memory cell update:

\( {C_{t}}={f_{t}}\cdot {C_{t-1}}+{i_{t}}\cdot \widetilde{{C_{t}}}\ \ \ （5） \)

Output gate:

\( {o_{t}}=σ({W_{o}}[{h_{t-1}},{x_{t}}]+{b_{o}})\ \ \ （6） \)

Hidden state update:

\( {h_{t}}={o_{t}}\cdot tanh{({C_{t}})}\ \ \ （7） \)

Among them, the weight matrix is represented by \( W \) , the bias vector is represented by \( b \) , \( σ \) is defined as the Sigmoid function, \( tanh \) is the definition of the hyperbolic tangent function, \( {x_{t}} \) represents the current input, and the hidden state at the previous time step and the memory cell state at the previous time step are represented by \( {h_{t-1}} \) and \( {C_{t-1}} \) respectively.

2.3. Construction of LSTM load forecasting model ground on QPSO

Firstly, the data preparation work is carried out, which includes two steps: data preprocessing and data partitioning. In the data preprocessing stage, the original power load data and related influencing factor data (such as meteorological data, date types, etc.) are input. The missing values therein are filled by using the linear interpolation method, the noisy data are removed by applying the moving average filtering method, and then to map all the data into the interval [0, 1], the Min - Max normalization technique is adopted, and finally the preprocessed data are output. Next, the data partitioning step is entered. Taking the preprocessed data as input, 70% of the data is used for training, while 30% of the data is used for testing, dividing the data into two parts, and outputting the set used to train and the set used to test.

Subsequently, the step of optimizing the LSTM hyperparameters by QPSO is carried out. Firstly, the particle swarm is initialized. According to the determined hyperparameter dimension, that is, corresponding to the number of hyperparameters of the LSTM network to be optimized, the position of each particle and its individual optimum position are randomly initialized. Then, the global optimum position is found from the fitness value which is calculated. Next, the mean value of the individual optimum positions of every particle is calculated, and the initialized particle swarm is output. Immediately after that, the iterative update process is entered. Taking the state of the previous generation of particle swarm as input, a random number is generated for each particle, and the particle position is upgraded accordingly. The fitness value of the upgraded particle place is calculated, and the individual optimum position and the global optimum position are updated synchronously. The mean value of the individual optimum positions of every particle is calculated, and the updated particle swarm is output. Finally, the termination condition judgment is made. Combining the current state of the particle swarm and the number of iterations, it is checked whether the maximum number of iterations has been reached or whether the change in the aptness value is less than the preset threshold. If the condition is satisfied, the optimal combination of hyperparameters corresponding to the global optimal position is output; if not, the iterative update step is returned for re-operation.

After the hyperparameter optimization is completed, the LSTM model training stage is entered. Taking the training set and the optimal combination of hyperparameters found by QPSO as input, the LSTM network is configured according to the optimal hyperparameters to make it train on the training set. The weights and biases of the network are adjusted by means of the backpropagation algorithm to minimize the prediction error, and the trained LSTM model is output.

Finally, the model evaluation step is carried out. Taking the testing set and the trained LSTM model as input, the functionality of the model is assessed by the testing set. Specifically, various evaluation indicators of the prediction results are calculated, such as the root mean square error (RMSE), the mean absolute percentage error (MAPE), etc., and the results of the model assessment indicators are output to measure the performance of the model.

3. Case analysis

3.1. Dataset

The dataset adopted in this research covers load information under various working conditions such as different seasons, weekdays and holidays. The total amount of data is 336 pieces. This dataset contains multiple features, such as temperature, humidity, wind speed, etc., to comprehensively reflect the factors influencing the power load.

During the preprocessing process, the missing values were dealt with first. The missing data is filled using the linear interpolation method. Secondly, the data was normalized to map the values of all features onto the interval [0, 1] to eliminate the differences in the numerical magnitudes of different features.

The formula is:

\( {x_{norm}}=\frac{x-{x_{min}}}{{x_{max}}-{x_{min}}}\ \ \ （8） \)

among them, the original data is represented by \( x \) , and the minimum value and the maximum value of this feature are represented by \( {x_{min}} \) and \( {x_{max}} \) respectively.

The dataset was divided into a set used to train and a set used to test at a proportion of 7:3. This partitioning method can make sure that the model fully learns the characteristics of the data while effectively evaluating the generalizability of the model.

3.2. Network parameter settings

In this study, the LSTM model ground on Quantum Particle Swarm Optimization (QPSO) was used for load forecasting and compared with the LSTM model ground on Particle Swarm Optimization (PSO) and the traditional LSTM model.

3.2.1. LSTM model ground on quantum particle swarm optimization

The LSTM model optimized by the QPSO algorithm has a studying proportion of 0.0098. The quantity of LSTM network layers is configured as 2, and the quantities of neurons in the hidden layers are 187 and 199 respectively. The maximum number of iterations is 56.

3.2.2. LSTM model ground on particle swarm Optimization

The LSTM model optimized by the PSO algorithm has a studying proportion of 0.0065. The quantity of LSTM network layers is configured as 2, and the quantities of neurons in the hidden layers are 56 and 149 respectively. The maximum number of iterations is 80.

3.2.3. Traditional LSTM model

For the traditional LSTM model, the basic studying proportion is 0.005. The quantity of LSTM network layers is configured as 2, and the maximum number of iterations is 20.

3.3. Example Index

In order to evaluate the prediction accuracy, the Root Mean Square Error (RMSE) and the Mean Absolute Percentage Error (MAPE) are employed. The RMSE can reflect the average magnitude of the deviation between the predicted value and the true value, while the MAPE measures the relative size of the prediction error. The smaller the values of the two, the higher the prediction accuracy.

Table 1: Comparison of Different Algorithm Models.

It is evident from the tabular data (Table1) that the LSTM model ground on QPSO outperforms both the traditional LSTM model and the LSTM model ground on PSO in terms of the RMSE and MAPE metrics.

In addition, by plotting the typical daily electrical load forecasting curve (Figure 1), it can be intuitively found that the forecasting curve of the LSTM model based on QPSO possess the optimal degree of conformity to the actual load curve and can more accurately reflect the changing trend of the power load, further proving the superiority of this method in load forecasting.

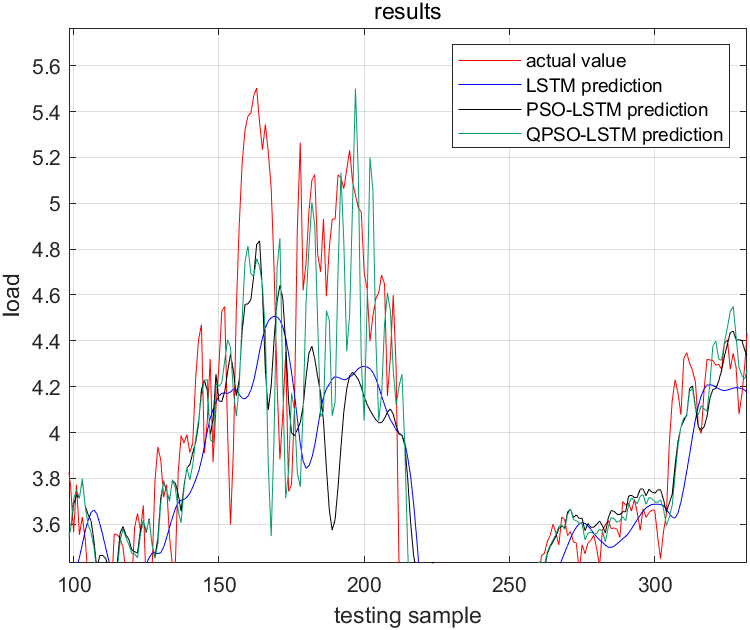
Figure 1: The typical daily electrical load forecasting curve. (Partial)

4. Conclusion

This paper provides a technique for electrical load forecasting using the Long Short-Term Memory Network (LSTM) ground on Quantum Particle Swarm Optimization (QPSO). The core of this method lies in the ingenious integration of two advanced technologies, namely, the unique gated structure of LSTM and the efficient search for the optimum fusion of model parameters by the QPSO algorithm, so as to conduct accurate power load forecasting.

Firstly, data preprocessing is carried out to handle the missing values and outliers and normalize the information. Then, the processed information is input into the Long Short-Term Memory Network (LSTM) model ground on Quantum Particle Swarm Optimization (QPSO) for training to obtain the optimized hyperparameters. Finally, highly representative test cases are handpicked to verify the training fruitfulness. The case analysis and comparison verify that the LSTM model ground on QPSO has advantages such as a high learning rate, better parameter optimization, and better adaptability to large amounts of data compared with the traditional LSTM model and other artificial intelligence algorithm models, thus solving the problem of power grid load forecasting.