1. Introduction

As a primary load-bearing form in bridges, buildings, and industrial facilities, steel structures undergo continuous deterioration due to fatigue, corrosion, and overload during long-term service. With increasing traffic demands, truss structures—characterized by stress concentration at nodes, sensitivity to dynamic loads, and challenges in detecting hidden damage—face heightened risks of failure. Maintenance costs for aging structures account for over 40% of total infrastructure investments in developed countries [1], underscoring the urgency for accurate reliability prediction to enhance safety and reduce rehabilitation expenses.

With the continuous advancement of theory and technology, numerous scholars worldwide have made innovative progress in applying Bayesian updating to study the reliability of bridge structures with diverse types and materials. For instance, Gong et al[2]. achieved more accurate reliability assessments for ancient stone arch bridges, exemplified by the Zhaozhou Bridge, using Bayesian updating methods. Ma introduced a Bayesian dynamic linear model to investigate the reliability of existing small- and medium-span bridges [3]. Xiao et al. employed the subset simulation-based BUS method to rapidly and accurately update parameters in chloride-induced durability models [4]. Internationally, Mohamad Salaheddine and Kaveh Arjomandi proposed a reliability-based framework for the evaluation and optimized maintenance of steel bridges [5]. R. Wang, L. Ma, C. Yan, and J. Mathew developed a novel structural reliability prediction method for steel bridges using dynamic object-oriented Bayesian networks (DOOBNs) [6]. Tran, T.-B., Bastidas-Arteaga, E., and Aoues (2020) presented a dynamic Bayesian network approach to update the reliability of deteriorating timber structures based on inspection data [7]. Yilmaz, M.F., Anghileri, M., Capacci, L., and Biondini, F. (2022) proposed a reliability assessment framework for reinforced concrete bridges exposed to corrosion, integrating lifecycle probabilistic methods with Bayesian updating to incorporate structural health monitoring data into simulation-based evaluations of deteriorating bridges [8]. Recognizing the critical relationship between modal parameters and reliability, Wang and Lin et al. applied Bayesian model updating techniques to identify modal parameters, thereby indirectly enabling structural reliability analysis [9][10].

Despite progress, Bayesian applications in truss reliability remain underexplored.This study establishes a Bayesian updating framework combined with ABAQUS finite element modeling to predict truss reliability under diverse loading conditions. The proposed methodology offers theoretical guidance for lifecycle reliability assessment of truss structures.

2. Bayesian theory

2.1. Bayesian framework

Bayesian theory is a statistical inference paradigm based on probability. Its core is to combine prior knowledge with observation data through dynamic updating to form quantitative cognition of unknown parameters or assumptions [11]. Different from the frequency school, Bayesian method regards parameters as random variables and emphasizes the rationality of subjective probability and iterative learning ability.

Bayesian update algorithm is a statistical inference method based on Bayesian theorem, which can continuously update the model parameters by calculating the posterior distribution combined with prior information and observation data. In truss reliability prediction, Bayesian updating can adjust the parameters in the empirical model according to the measured data and historical information, and greatly improve the accuracy. The core formula is:

\( P(θ|D)=\frac{P(D|θ)P(θ)}{P(D)}=\frac{P(D|θ)P(θ)}{\int P(D|θ)P(θ)dθ} \) (1)

where:

P(θ|D): Posterior probability reflecting updated parameter uncertainty.

P(D|θ): Likelihood function describing data generation under θ.

P(θ): Prior probability encoding initial parameter knowledge.

P(D): Marginal likelihood ensuring normalization.

The specific flow of Bayesian theory is as follows (Figure 1):

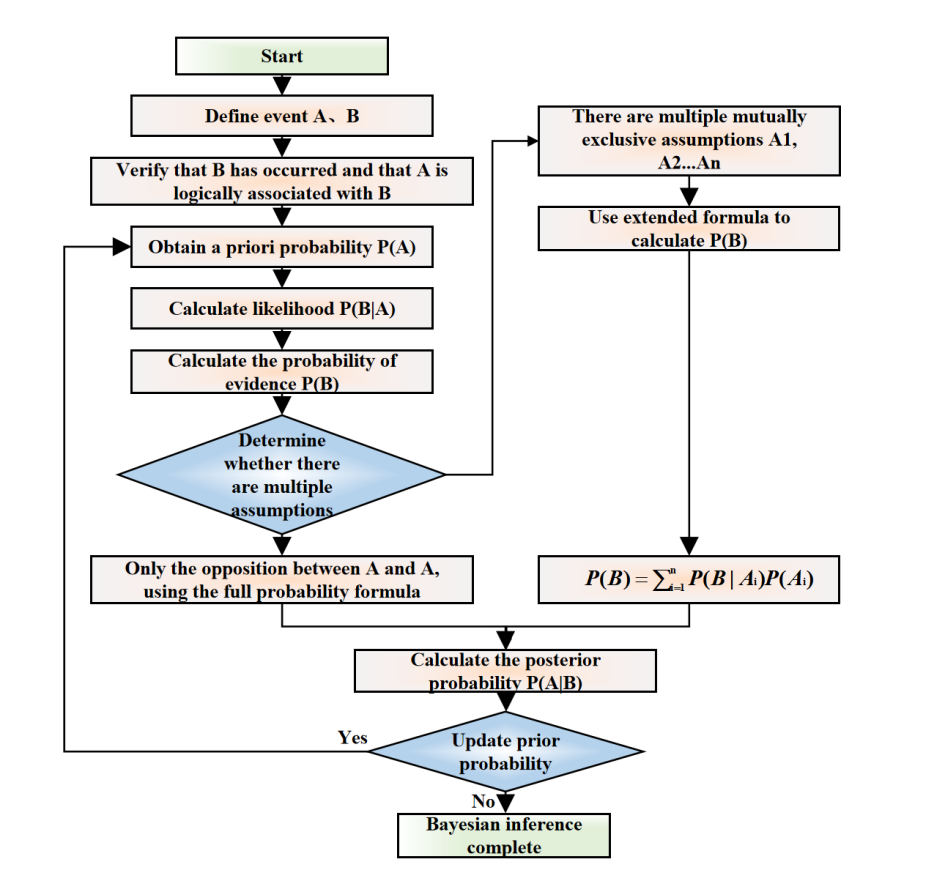
Figure 1: Bayesian theory flow chart

2.2. Prior distribution setup

The prior probability distribution can reflect the understanding of model parameters without new observation data. Taking a truss structure as an example, it is assumed that the elastic modulus of its upper and lower chords and web members obey normal distribution:

\( EA~N({μ_{EA}},σ_{EA}^{2}) \) (2)

The mean value is taken from the material manual (e.g. the typical value of steel is 2.0 × 10⁵Mpa), and the standard deviation reflects the fluctuation of the production batch (e.g. zone 5%)

For the failure probability θ of key members (such as compression webs), in the absence of specific historical data, we assume that the failure probability θ follows a uniform distribution θ~U(0.0.05), covering a reasonable range of failure probability.

2.3. Likelihood function construction

The establishment of likelihood function is the key link of Bayesian renewal theory, which needs to be based on truss mechanics model and observation data. In truss reliability analysis, the likelihood function based on node displacement observation data needs to quantify the difference between the predicted value of the theoretical model and the measured value, and its core is to describe the joint impact of measurement error and parameter uncertainty on the data through the probability model [12].

For the truss node displacement data, the likelihood function predicts the displacement value through the theoretical mechanical model, and assumes that the difference between the measured value and the theoretical value is independent and obeys the normal distribution. The likelihood function can be expressed as:

\( P(D|θ)=\prod _{i=1}^{n}\frac{1}{\sqrt[]{2πσ_{i}^{2}}}exp(-\frac{{(d_{i}^{obs}-d_{i}^{model})^{2}}}{2σ_{i}^{2}}) \) (3)

Where, \( d_{i}^{obs} \) is the measured data and \( d_{i}^{model} \) is the predicted value of the model.

3. Case study

3.1. Project overview

In this paper, Zhangyan bridge is selected as the specific research engineering background. Zhangyan bridge is located in Fengxiang village, Qinnan Town, Yandu District, Yancheng City. The truss bridge has a span of 5×20+81.96+5×20 meters, a total width of 7.0m, two-way two lane, and the main bridge adopts through steel truss beam structure (Figure. 2).

Figure 2: Structural drawing of swallow bridge

In order to simplify the calculation, the most representative span is selected for this study. Because it is a symmetrical structure, and the middle span has the largest bending moment and larger displacement, it is more prone to fatigue damage. It has been several years since the bridge was initially built, and the predicted value of the model is a priori number. There is a certain error between it and the measured value today, because the tensile and compressive stiffness EA of the bridge will decrease year by year during the service period, especially in the middle span. Therefore, the middle span with the greatest risk is selected for this study. The model diagram is shown in Figure 3:

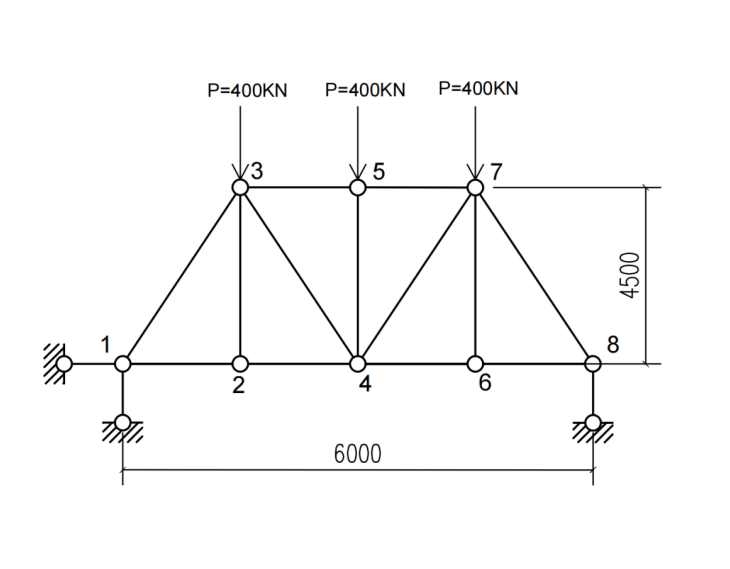
Figure 3: Simplified model diagram

The model parameters are determined by the specific data of Zhangyan Bridge:

(1) Span: 6m truss height: 4.5m

(2) Top chord EA₁, web member bottom chord EA₂, bottom chord EA₃ (EA₁=EA₃)

(3) Apply three concentrated loads p=400kn at the apex 3, 5 and 7

(4) The measured vertical displacement of 4 points is 17.4mm, the vertical displacement of 6 points is 13.9mm, and the lateral displacement of 3 points is 1.47mm

(5) EA₁ obeys normal n (800000KN, 80000KN); EA₂ obeys uniform U (250000KN, 320000KN) as a priori and updates EA₁ and EA₃. (EA₁ error conforms to the normal distribution with standard deviation of 2.0mm, and EA₂ error conforms to the normal distribution with standard deviation of 0.2mm)

3.2. Displacement analysis

The virtual work principle is based on the law of conservation of energy and is widely used in the displacement analysis of truss structures. When there is no external force acting on the target node, the displacement calculation problem can be solved by applying virtual force. Virtual work equation: \( 1\cdot Δ=∫u\cdot dL \) and its application in integral truss: \( 1\cdot Δ=∑\frac{nNL}{EA} \) it provides a theoretical basis for this.

Taking three vertical 400kN concentrated loads on the top as an example, the specific displacement calculation formula is as follows:

\( {Δ_{4}}=\frac{2P}{EA1}+\frac{10\sqrt[]{10P}}{EA2}+\frac{P}{4EA3} \) (4)

\( {Δ_{6}}=\frac{P}{3EA1}+\frac{5\sqrt[]{10}}{2EA2}+\frac{P}{2EA3} \) (5)

\( {Δ_{3}}=\frac{P}{EA1}+\frac{3P}{2EA3} \) (6)

The theoretical value of each node displacement can be calculated through the above formula, and the results are summarized in the following table 1:

Table 1: Calculated and measured displacement of each node

3.3. Finite element validation

ABAQUS is a set of powerful finite element software for engineering simulation. It has powerful modeling ability, can simulate a variety of material properties, and can consider the nonlinear characteristics of materials such as molding and fatigue. In conclusion, it can effectively simulate the structural displacement results. Therefore, ABAQUS software is used for static analysis in this study.

Truss element is used in the simulation, and the EA values of chords and webs are taken as the mean value of the distribution. The results are as follows (Figure 4):

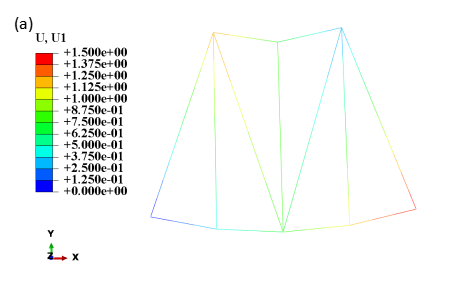
Figure 4: Displacements under vertical loads (a) horizontal (b) vertical

4. Reliability prediction under different loading modes

4.1. Vertical load effects

Vertical load is the main stress form of truss structure, which directly affects the internal force distribution of members, and then determines the sensitivity of EA parameters to structural response. By applying vertical loads with different distributions, the strain or displacement response data of members under actual working conditions can be simulated to provide observation values for Bayesian update. By applying vertical concentrated loads at different nodes, the strain or displacement response data of members under actual working conditions can be simulated to provide observation values for Bayesian update.

If the prior distribution assumes a high EA value, but the load test shows that the large deformation Bayesian update will correct the EA posterior distribution to shift to low stiffness, reflecting the potential material degradation.

When the vertical concentrated load is 400KN and is set at nodes 3, 5 and 7 respectively, the displacement values of nodes 3, 4 and 6 are monitored. If the prior upper chord EA₁ and lower chord EA₃ obey normal distribution (800000KN, 80000KN) (Figure 5), web member EA₂ obeys uniform distribution (250000KN, 320000KN), the posterior update is that EA₁ and EA₃ obey normal distribution (795000KN, 80000KN), and EA₂ obey normal distribution (260000KN, 6700KN) (Figure 5). It can be seen that through Bayesian updating, the standard deviation of EA₁ (upper chord) and EA₃ (lower chord) decreased from 800000KN to 795000KN (the decrease was not significant), the distribution range of EA₂ (web member) was compressed from uniform distribution to normal distribution, and the uncertainty of EA₂ was effectively controlled. Because the update effect of EA₁ and EA₃ is not significant, change the load mode and continue to update.

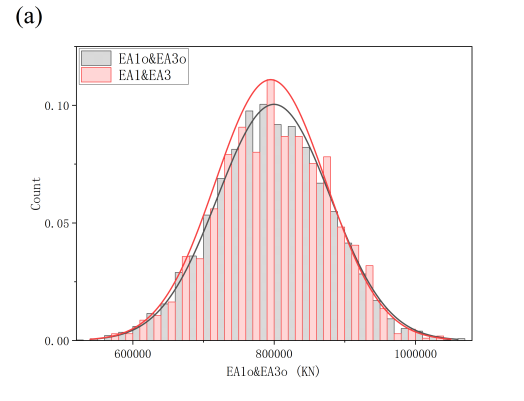
Figure 5: Update effect under vertical load mode

(a) Prior and posterior distribution of EA₁&EA₃ under vertical load mode

(b) Prior and posterior distribution of EA₂ under vertical load mode

4.2. Horizontal load effects

Change the vertical load to the horizontal load and continue to update the data. Both wind load and seismic force belong to lateral load, which may cause significant lateral displacement. Therefore, the setting of lateral load is also very important to predict the integrity and reliability of the structure.

When 400KN transverse concentrated load is set at nodes 3 and 7 respectively, the transverse displacement of nodes 3 and 7 is monitored respectively. The prior distribution of EA value is consistent with that of vertical load. A posteriori update shows that EA1 and EA3 obey normal distribution (788000KN, 80000KN), and EA2 obey normal distribution (260000KN, 4700KN) (Figure. 6). It can be seen that through Bayesian updating, the average value of EA1 (upper chord) and EA3 (lower chord) decreased from 800000KN to 78000000KN, the distribution range of EA3 (web member) was compressed from uniform distribution to normal distribution, and the uncertainty of key parameters was effectively controlled.

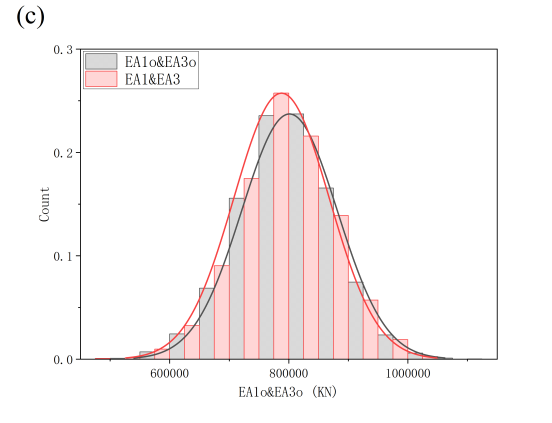
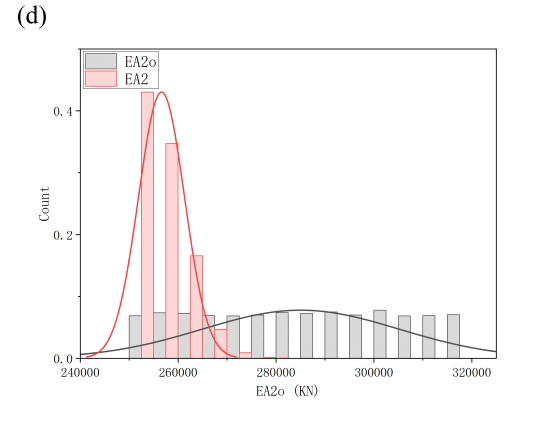
Figure 6: Update effect diagram under horizontal load mode

(c) Prior and posterior distributions of EA₁&EA₃ under horizontal load mode

(d) Prior and posterior distribution of EA₂ under horizontal load mode

5. Conclusions

Based on ABAQUS finite element simulation platform and Bayesian parameter updating theory, this study constructed the reliability evaluation model of bridge truss structure:

The research confirms that Bayesian method can correct the cognitive deviation of member stiffness through limited monitoring data under different load types, reflecting its adaptability under different stress scenarios. It is worth noting that the web member (EA₂) shows significant sensitivity in the updating process, which provides a theoretical basis for the selection of priority parameters in engineering monitoring. In the future, the dynamic Bayesian network (DBN) is introduced to dynamically associate the time-series load data with the structural response to realize the real-time tracking of parameter degradation and quantitative characterization of damage accumulation; On the other hand, it breaks through the limitation of single mechanical monitoring, couples multi-dimensional information such as environmental temperature and humidity, material corrosion rate, and constructs hierarchical Bayesian model to improve the effect of parameter update and long-term prediction accuracy.

Authors contribution

All the authors contributed equally and their names were listed in alphabetical order.