1. Introduction

1.1. History of the 15-puzzle and its generalizations

The well known intellectual game with 15 numbered square counters has a ancient and remarkable history. The game was created by Noyes Chapman and it was first appeared in the 1870s. It spread quickly and soon it became extremely popular in the United States and Europe. This is W. Arens’s comments on the influence of 15-puzzle:“Here you could even see the passengers in horse trams with the game in their hands. In offices and shops bosses were horrified by their employees being completely absorbed by the game during office and class hours. Owners of entertainment establishments were quick to latch onto the rage and organized large contests. The game had even made its way into solemn halls of the German Reichstag."In the 1900’s, many people worked tirelessly to solve the problems related to the 15-puzzle, but actually some of them can be seen to be unsolvable due to the power of mathematics. Of course, the most famous issue must be the problem proposed by the impish puzzle maker Sam Loyd. He offered a prize of 1000 dollars for the first correct solution to the problem however it has never been claimed.This is because it is impossible to solve this challenge. People first proved it at the end of 19th century by permutation parity. In the solved state, the permutation is even but swapping only 14 and 15 create an odd permutation.Since then, many extensions of the 15-puzzle have been proposed and studied. [1] studied puzzles with more than 1 empty space, [2] studied puzzles with tiles that are rotatable, and puzzles that allowed rotation without an empty space were discussed in [3].A well-known generalization of the 15-puzzle is that of R. M. Wilson in 1974, where numbered tiles are slid across edges in a graph. Formally, vertices are labeled with numbers, with one vertex labeled the empty space, and we are allowed to swap a numbered label and an adjacent empty label.In his paper [4], he found the group of permutations for non-separable simple graphs. His theorem is sometimes called Wilson’s theorem.

1.2. Contents and paper structure

Building on the generalization of the 15-puzzle onto sliding graph puzzles, we find the group of permutations of labels on sliding graph puzzles that are simple and non-separable using similar ideas as [4], by first finding the group on theta graphs and then inducting on the cyclomatic number. We use a more direct approach in the proof, explicitly finding sequences of moves that carries out certain permutations or generates certain groups. This aids the process of following this proof to create a manual algorithm to solving any sliding graph puzzle. Following this manual algorithm, one can theoretically carry out a sequence of moves to solve any scrambled state of any non-separable sliding graph puzzle. The algorithm is recursive, reducing the cyclomatic number of the unsolved portion of the graph until the problem is reduced to solving a theta graph, which is done directly.

We extend Wilson’s result on the permutation group for a non-separable graph to one that applies to any finite simple graph, and present a new brief proof of the 1-connected and disconnected cases by discussing the movement of tiles across articulation vertices. We also propose a generalization of the manhattan distance metric to any sliding graph, and explore the performance of the A* and suitably weighted A* algorithms in graphs with different cyclomatic numbers.

In section 2, we present an overview of the group theory and permutation groups needed in later discussions. In section 3, we represent states of the 15-puzzle with a permutation and use group theory to show that only states with even permutations can be achieved. In section 4, we show Wilson’s generalization of the 15-puzzle and present our proof of Wilson’s theorem. In section 5, we extend Wilson’s theorem to 1-connected, disconnected, polygon, and non-simple graphs. In section 6, we present a manual algorithm for solving any non-separable graph puzzle. In section 7, we attempt to generalize A* algorithms on the 15-puzzle to solve any sliding graph puzzle. In section 8, we end the paper with suggestions for future work.

2. A review of group theory and permutation groups

In this section, we introduce group theory and permutation groups to aid the discussion in later sections. We see in section 3 and 4 that states on the 15-puzzle and sliding graph puzzles in general can be represented as permutation, and group theory tools are useful for generating and constructing certain permutation groups, such as that of  $$ {\mathrm{\theta }}_0$$  (see section 4.3).

2.1. Groups and relevant theorems

Definition 2.1. A subset  $$ \mathrm{S}$$  of a group  $$ \mathrm{G}$$  generates  $$ \mathrm{G}$$  if every element of  $$ \mathrm{G}$$  can be expressed as a finite product of elements from  $$ \mathrm{S}$$  and their inverses.

Definition 2.2. A homomorphism is a function between two groups  $$ \mathrm{\phi }:\mathrm{A}\mapsto \mathrm{B}$$  such that  $$ \mathrm{\phi }(\mathrm{a}\cdot \mathrm{b})=\mathrm{\phi }\left(\mathrm{a}\right)\cdot \mathrm{\phi }\left(\mathrm{b}\right)$$ . An isomorphism is a bijective homomorphism. Two groups are isomorphic if there exists an isomorphism from one group to the other.

Definition 2.3. The image of a homomorphism  $$ \text{Im}\left(\mathrm{\phi }\right)$$  is the subgroup  $$ \left\{\mathrm{\phi }\right(\mathrm{a}):\mathrm{a}\in \mathrm{A}\}$$  of  $$ \mathrm{B}$$ . The kernel of a homomorphism  $$ \text{ker}\left(\mathrm{\phi }\right)$$  is the subgroup  $$ \{\mathrm{a}:\mathrm{\phi }(\mathrm{a})={\mathrm{e}}_{\mathrm{B}}\}$$ .

Theorem (Lagrange theorem). For a finite group  $$ \mathrm{G}$$  and subgroup  $$ \mathrm{H}\le \mathrm{G}$$ ,  $$ \left|\mathrm{H}\right|$$  divides  $$ \left|\mathrm{G}\right|$$ .

Definition 2.4. A Sylow p-subgroup is a subgroup with order  $$ {\mathrm{p}}^{\mathrm{k}}$$  for maximal  $$ \mathrm{k}$$ .

Theorem (Second Sylow theorem). If  $$ {\mathrm{P}}_1$$  and  $$ {\mathrm{P}}_2$$  are 2 Sylow p-subgroups, then there exists  $$ \mathrm{g}$$  with  $$ \mathrm{g}{\mathrm{P}}_1{\mathrm{g}}^{-1}={\mathrm{P}}_2$$ .

Theorem (First isomorphism theorem). Let  $$ \mathrm{f}:\mathrm{G}\mapsto \mathrm{H}$$  is a group homomorphism. Then  $$ \mathrm{G}/\text{ker}\left(\mathrm{f}\right)\cong \text{Im}\left(\mathrm{f}\right)$$ . In particular,  $$ \left|\mathrm{G}\right|=\left|\text{ker}\right(\mathrm{f}\left)\right|\left|\text{Im}\right(\mathrm{f}\left)\right|$$ .

2.2. Permutations and permutation groups

Definition 2.5. A permutation of a finite set is a rearrangement of its elements, defined as a bijective function (a one-to-one and onto mapping) from the set to itself. A transposition is a permutation that swaps two elements in a set while leaving all other elements unchanged.

Definition 2.6. A permutation is even if it can be expressed as a product of an even number of transpositions. A permutation is odd if it can be expressed as a product of an odd number of transpositions.

Definition 2.7. The symmetric group  $$ {\mathrm{S}}_{\mathrm{n}}$$  is the group of all permutations of a finite set of  $$ \mathrm{n}$$  elements. The group of all permutations on a set  $$ \mathrm{X}$$  is denoted by  $$ \text{Sym}\left(\mathrm{X}\right)$$ . The alternating group  $$ {\mathrm{A}}_{\mathrm{n}}$$  is the group of all even permutations of a finite set of  $$ \mathrm{n}$$  elements. It is a subgroup of the symmetric group  $$ {\mathrm{S}}_{\mathrm{n}}$$ . The alternating group on a set  $$ \mathrm{X}$$  is denoted by  $$ \mathrm{A}\mathrm{l}\mathrm{t}\left(\mathrm{X}\right)$$ .

Permutations can be expressed using cycle notation, where the elements in the brackets are in one cycle. Each element maps to the next in the cycle, and the last element maps to the first. Every permutation can also be written as a product of transpositions. Below is an example:

$$$ \begin{array}{c}(\mathrm{1,3},\mathrm{7,2},\mathrm{5,11,10,8},\mathrm{4,9},\mathrm{6,13})\left(\mathrm{14,15}\right)=\\ \left(\mathrm{1,3}\right)\left(\mathrm{1,7}\right)\left(\mathrm{1,2}\right)\left(\mathrm{1,5}\right)\left(\mathrm{1,11}\right)\left(\mathrm{1,10}\right)\left(\mathrm{1,8}\right)\left(\mathrm{1,4}\right)\left(\mathrm{1,9}\right)\left(\mathrm{1,6}\right)\left(\mathrm{1,13}\right)\left(\mathrm{14,15}\right).\end{array}$$$

In this paper, we use the convention that permutations are evaluated from left to right, or in other words, that the group action of  $$ {\mathrm{S}}_{\mathrm{n}}$$  on  $$ \left[\mathrm{n}\right]$$  is a right action.

Proposition 2.8. The alternating groups  $$ {\mathrm{A}}_{\mathrm{n}}$$  can be generated by 3-cycles.

Proof. By definition, every even permutation can be written as a product of an even number of transpositions. Separating this product into pairs of transpositions, the following three cases arise, where a,b,c,d are distinct elements:

1.  $$ (\mathrm{a},\mathrm{b})(\mathrm{a},\mathrm{b})$$  is the identity permutation

2.  $$ (\mathrm{a},\mathrm{b})(\mathrm{a},\mathrm{c})=(\mathrm{a},\mathrm{b},\mathrm{c})$$ , a 3-cycle

3.  $$ (\mathrm{a},\mathrm{b})(\mathrm{c},\mathrm{d})=(\mathrm{a},\mathrm{b},\mathrm{c})(\mathrm{a},\mathrm{d},\mathrm{c})$$ , a product of 3-cycles

Since the product of every two transpositions can be expressed as a product of 3-cycles, it follows that the alternating group  $$ {\mathrm{A}}_{\mathrm{n}}$$  can be generated by all 3-cycles.  □

Proposition 2.9. The alternating group can be generated by  $$ (\mathrm{a},\mathrm{b},\mathrm{k})$$ , where  $$ \mathrm{a}$$  and  $$ \mathrm{b}$$  are fixed distinct elements, and  $$ \mathrm{k}\in \left[\mathrm{n}\right]-\{\mathrm{a},\mathrm{b}\}$$ .

Proof. Since all alternating group can be generated by 3-cycles, we only need to prove  $$ (\mathrm{a},\mathrm{b},\mathrm{k})$$  can generate all 3-cycles.Let a and  $$ \mathrm{b}$$  be two fixed distinct elements in  $$ \left[\mathrm{n}\right]$$ . We show that any 3-cycle  $$ (\mathrm{x},\mathrm{y},\mathrm{z})$$  can be expressed as a product of 3-cycles of the form  $$ (\mathrm{a},\mathrm{b},\mathrm{k})$$ , where  $$ \mathrm{k}\in \left[\mathrm{n}\right]-\{\mathrm{a},\mathrm{b}\}$$ .Case 1:  $$ \{\mathrm{x},\mathrm{y},\mathrm{z}\}\cap \{\mathrm{a},\mathrm{b}\}=\mathrm{\varnothing }$$ If  $$ \mathrm{x},\mathrm{y},\mathrm{z}$$  are distinct from  $$ \mathrm{a}$$  and  $$ \mathrm{b}$$, then:

$$$ (\mathrm{x},\mathrm{y},\mathrm{z})=(\mathrm{a},\mathrm{b},\mathrm{x})(\mathrm{a},\mathrm{b},\mathrm{y}{)}^{-1}(\mathrm{a},\mathrm{b},\mathrm{z}).$$$

Case 2: If  $$ \mathrm{x},\mathrm{y},\mathrm{z}$$  share one element with  $$ \{\mathrm{a},\mathrm{b}\}$$, we consider the following subcases:

Case3: Two elements equal to a and b

If two elements of {x,y,z} are equal to a and b,we have:

In all cases, any 3-cycle  $$ (x,y,z)$$  can be expressed as a product of 3-cycles of the form  $$ (a,b,k)$$ . Therefore, all 3-cycles can be generated by  $$ (a,b,k)$$ .  □

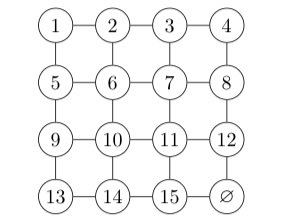
3. The permutation group of 15-puzzle

In this section, we represent states of the 15-puzzle as permutations, and demonstrate that the set of all legal permutations in the puzzle is isomorphic to  A15 .

According to definition 2.7, the set of all states of the 15-puzzle is a subgroup of  Sn . Here is an example:

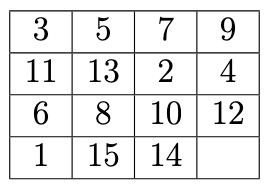
We can represent this state of the 15-puzzle using cycle notation:

$$$ \sigma =(\mathrm{1,3},\mathrm{7,2},\mathrm{5,11,10,8},\mathrm{4,9},\mathrm{6,13})\left(\mathrm{14,15}\right).$$$

When we consider that the position of the blank space remains unchanged between the initial and goal states, the number of moves the blank space makes upward should be equal to the number it makes downward, and the number of moves it makes left should be equal to the number it makes right. Therefore, only when the initial state of 15-Puzzle that is an even permutation can be solved. Therefore, the state where tiles 14 and 15 are swapped cannot be solved because it is an odd permutation.

Using this logic, we only prove that the 15-puzzle is a subgroup of the alternating group, and we still need to determine whether all even permutations can be solved. To prove that all even permutations can be solved, we largely follow the process in [5] and we use Propositions 2.8 and 2.9 from the previous section.

Firstly, we construct a 3-cycle  $$ \left(\mathrm{11,12,15}\right)$$ . The initial state is shown at the beginning of Fig. 3.2. By sliding these tiles, we generate the cycle  $$ \left(\mathrm{11,12,15}\right)$$ .

The next step is constructing "the long cycle",  ρ  = (1, 2, 6, 7, 3, 4, 8, 15, 10, 14, 13, 9, 5). This cycle is constructed by temporarily displacing tiles 11 and 12 from their original slots and do a sequence of moves. we first change the position of the right bottom corner to that of Fig. 3.3 and move all the tiles except 11 and 12 through the path shown in Fig. 4, and the 15-puzzle will look like Fig. 5.

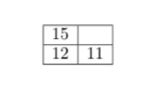
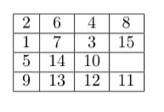
Finally, we restore the positions of 11 and 12 and this is the entire long cycle  ρ .

The purpose of  ρ  is to move a random tile k to the bottom right corner where the previous three cycle (11,12,15) can act on them. For example, if we want to generate the cycle (3,11,12), we need to apply  ρ10  to move the tile 3 to slot 15. Then we can apply the previous 3 cycle  (11,12,15) , but tile 3 is at slot 15 so the cycle actually swaps tile 11 12 and 3, shown in Fig. 3.6. Finally, we only need to apply  ρ−10 to restore all other tiles to their original positions and we can generate the cycle  (3,11,12)$ , shown in Fig. 3.7.

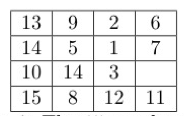
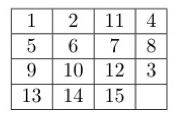
Through this example, we can see that by conjugating the fixed 3-cycle  $$ \left(\mathrm{11,12,15}\right)$$  with powers of  $$ \rho $$ , it can generate all 3-cycles of the form  $$ (\mathrm{11,12},k)$$ , where  $$ k\in \{\mathrm{1,2},\dots ,15\}-\left\{\mathrm{11,12}\right\}$$ . Proposition 2.9 has already proved that 3-cycle (a,b,k) can generate the alternating group  $$ A_{15}$$ , so together with the fact that the permutation group of the 15-puzzle is a subgroup of  $$ A_{15}$$ , we can conclude that the permutation group of 15-puzzle is isomorphic to  $$ A_{15}$$ .

4. Puzzle group of generalized sliding graph puzzles

In this section, we will generalize the permutation group of the 15-puzzle following the discussion in [4], and provide a variation of a proof of Wilson’s theorem so as to aid the discussion in section 6.

4.1. Generalizing the 15-puzzle

We introduce the following graph theoretic terms to generalize the 15-puzzle.

Definition 4.1. A graph is a collection of vertices (also called nodes) connected by edges. An edge connects 2 vertices. An undirected graph is a graph where no edge has an associated direction. The set of vertices of a graph  $$ G$$  is often denoted as  $$ V\left(G\right)$$ .

Assume from now on that every graph considered is undirected.

Definition 4.2. A simple graph is an undirected graph without loops (edges connecting from a vertex to itself), and any two edges must not have the same end vertices.

Definition 4.3. A path is a sequence of vertices  $$ (x_1,x_2,...,x_n)$$  such that any  $$ x_i$$  and  $$ x_{i+1}$$  are adjacent (connected by an edge). A simple path is a path with a non-repeating sequence of vertices.

Definition 4.4. A connected graph is a graph where there exists a path between any pair of vertices. A disconnected graph is a graph that is not connected. An articulation vertex (also cut vertex) of a connected graph is a vertex that, when removed, yields a disconnected graph. A non-separable (also biconnected, 2-connected) graph is a connected graph with no articulation vertices, or a graph with 1 vertex.

Definition 4.5. A bipartite graph is a graph such that each element can be labeled with ’a’ or ’b’ with every edge connecting between a vertex labeled ’a’ and a vertex labeled ’b’. Equivalently, every path from a vertex to itself must have even length (pass through an even number of edges). A non-bipartite graph is a graph that is not bipartite.

Let  $$ G$$  be a finite simple graph and label the vertices with numbers, leaving one vertex blank as the empty space  $$ \mathrm{⌀}$$ . This creates a 15-puzzle-like sliding graph puzzle.

Formally define a labeling on the graph  $$ G$$  with  $$ n+1$$  vertices as a bijective function  $$ f:V\left(G\right)\mapsto \{\mathrm{1,2},...,n,\mathrm{⌀}\}$$  that maps every vertex to its label. Let  $$ x$$  be a vertex such that  $$ f\left(x\right)=\mathrm{⌀}$$ , let two labelings  $$ f$$  and  $$ g$$  be adjacent if  $$ g\left(x\right)=f\left(y\right)\text{ and }g\left(y\right)=\mathrm{⌀}$$  for some vertex  $$ y$$  adjacent to  $$ x$$  (meaning they are connected with an edge), and  $$ f\left(k\right)=g\left(k\right)$$  for all vertices  $$ k\notin \{x,y\}$$ . Define a move to be the relabeling of a graph by an adjacent labeling. Define the puzzle group of a graph  $$ G$$  by  $$ P_G$$ , containing a permutation of  $$ \{\mathrm{1,2},...,n\}$$  for every labeling  $$ f$$  with  $$ s^{-1}\left(\mathrm{⌀}\right)=f^{-1}\left(\mathrm{⌀}\right)$$  that can be reached from a sequence of moves starting with the solved state labeling,  $$ s$$ , under composition of permutations. This coincides with the homotopy group of the graph. We denote the permutation of labelings e.g.  $$ f\left(a\right),f\left(b\right),f\left(c\right)$$  with vertices directly e.g.  $$ \left(abc\right)$$ .

We first prove the following useful proposition:

Proposition 4.6. Let  $$ G$$  be a finite simple connected graph. Then given two solved states  $$ s_1$$  and  $$ s_2$$ , the puzzle group with respect to  $$ s_1$$  is isomorphic to the puzzle group with respect to  $$ s_2$$ .

Proof. Let  $$ P_G\left(s_1\right)$$  and  $$ P_G\left(s_2\right)$$  be the puzzle groups with respect to  $$ s_1$$  and  $$ s_2$$  respectively. We can create an isomorphism  $$ \phi :P_G\left(s_1\right)\mapsto P_G\left(s_2\right)$$  by starting with the state  $$ s_2$$ , moving the blank space to  $$ s_1^{-1}\left(\mathrm{⌀}\right)$$ , carrying out a permutation  $$ p_1$$  in  $$ s_1$$ , and moving the blank space back to  $$ s_2^{-1}\left(\mathrm{⌀}\right)$$  along the same path. The permutation  $$ p_2$$  corresponding to this must be in  $$ P_G\left(s_2\right)$$  since  $$ p_1$$  can be reached with a sequence of moves, meaning  $$ p_2$$  can as well. Since carrying out a different permutation  $$ p_{1^{\mathrm{\text{'}}}}$$  must result in a different permutation  $$ p_{2^{\mathrm{\text{'}}}}$$ ,  $$ \phi $$  is injective. If there exists a sequence of moves bringing  $$ s_2$$  to some  $$ f_2$$ , corresponding to a permutation in  $$ P_G\left(s_2\right)$$ , then, moving the blank space to  $$ s_1^{-1}\left(\mathrm{⌀}\right)$$ , there must be a sequence of moves corresponding to a permutation in  $$ P_G\left(s_1\right)$$ , hence  $$ \phi $$  is surjective. The following 2 processes are equivalent:

1. Moving the blank space to  $$ s_1^{-1}\left(\mathrm{⌀}\right)$$ 

2. Carrying out  $$ p_1$$ 

3. Moving the blank space to  $$ s_2^{-1}\left(\mathrm{⌀}\right)$$ 

4. Moving the blank space to  $$ s_1^{-1}\left(\mathrm{⌀}\right)$$ 

5. Carrying out  $$ q_1$$ 

6. Moving the blank space to  $$ s_2^{-1}\left(\mathrm{⌀}\right)$$ 

and

1. Moving the blank space to  $$ s_1^{-1}\left(\mathrm{⌀}\right)$$ 

2. Carrying out  $$ p_1{q}_1$$ 

3. Moving the blank space to  $$ s_2^{-1}\left(\mathrm{⌀}\right)$$ 

hence  $$ \phi \left(p_1{q}_1\right)=\phi \left(p_1\right)\phi \left(q_1\right)$$ , and so  $$ \phi $$  is a well-defined homomorphism. Thus,  $$ \phi $$  is an isomorphism.  □

The puzzle group for any non-separable graph can be determined by the following theorem. Wilson’s theorem is applied to puzzle groups as follows:

Theorem 4.7 Let  $$ G$$  be a finite simple non-separable graph other than a polygon or the graph  $$ {\theta }_0$$  shown in Fig. 4.3. Then,  $$ P_G=\text{sym}\left(V\right(G)-\{f^{-1}\left(\mathrm{⌀}\right)\left\}\right)$$ , unless  $$ G$$  is bipartite, in which case  $$ P_G=\text{alt}\left(V\right(G)-\{f^{-1}\left(\mathrm{⌀}\right)\left\}\right)$$ . If  $$ G={\theta }_0$$ , then  $$ P_G\subset \text{sym}\left(V\right(G)-\{f^{-1}\left(\mathrm{⌀}\right)\left\}\right)$$  is a transitive subgroup of  $$ S_6$$  isomorphic to  $$ S_5$$ .

Remark. When  $$ G$$  is 1-connected (separable and connected), the puzzle group is no longer transitive and this case is dealt with in Theorem 5.1.

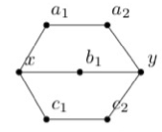
4.2. Wilson’s theorem on theta graphs

To prove Theorem 4.7, we largely follow Wilson’s proof in [2]. It is sufficient to prove a weaker result on theta-graphs, which are obtained by subdivisions of the graph shown in Fig. 4.4 that are simple. Start with some arbitrary theta-graph, and attempt to generate the alternating group or symmetric group from a sequence of moves. Denote a theta graph using the length of the simple paths from x to y. For example, consider the (2,2,3) theta graph in Fig. 4.5, with  $$ x$$ ,  $$ y$$ ,  $$ a_i$$ ,  $$ b_i$$ ,  $$ c_i$$  denoting vertices.

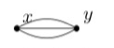
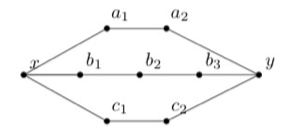
Since the puzzle group stays unchanged when the solved state is changed, choose a solved state such that  $$ s^{-1}\left(\mathrm{⌀}\right)\notin \{x,y\}$$ . In the example Fig. 4.5, let  $$ s^{-1}\left(\mathrm{⌀}\right)=c_1$$ . Consider the following 2 permutations  $$ \left(a_1{a}_{2}y{b}_3{b}_2{b}_1\right)$$  and  $$ \left(b_3{b}_2{b}_{1}x{a}_1{a}_2\right)$$  which are in  $$ P_G$$  due to the sequences of moves shown by listing the sequence of vertices the blank label is moved to: $$ c_1,x,b_1,b_2,b_3,y,a_2,a_1,x,c_1$$  and  $$ c_1,c_2,y,a_2,a_1,x,b_1,b_2,b_3,y,c_2,c_1$$  respectively. (By moving the blank label along the above sequence, we carry out the permutations in question.) Attempting to generate a group, we prove the following lemma, also proposed in [4]:

Lemma 4.8. Let  $$ S≔\{x,a_1,...,a_m,y,b_n,...,b_1\}$$  and let permutations  $$ p_1≔(a_1{a}_2\cdots a_{m}y{b}_n\cdots b_2{b}_1)$$  and  $$ p_2≔(b_n\cdots b_2{b}_{1}x{a}_1{a}_2\cdots a_m)$$ . Then:

$$$ ⟨p_1,p_2⟩=\{\begin{array}{cc}sym\left(S\right)& (m+n\text{ odd, }\{m,n\}\ne \{\mathrm{1,2}\left\}\right)\\ alt\left(S\right)& (m+n\text{ even, }\{m,n\}\ne \{\mathrm{2,4}\},m,n\ne 2)\\ & \end{array}$$$

Proof. Instead of using the doubly transitive property of  $$ S$$  in the proof in[4], we explicitly construct all 3-cycles needed to apply Proposition 2.9, which will aid the discussion in section 6.Let  $$ n\ge m\ge 3$$ . It is shown in [4] that the permutation

$$ p_3=\left(x{b}_{m-1}{a}_1\right)=p_2^{-1}{p}_1^m{p}_2^{-1}{p}_1^{1-m}{p}_2^{-2}{p}_1{p}_2^{-1}{p}_1{p}_2^2{p}_1^{m-1}{p}_2^{-1}{p}_1^{2-m}\in ⟨p_1,p_2⟩$$ .

We can deduce by symmetry and show that

$$ p_4=\left(y{b}_{n-m+2}{a}_m\right)=p_1{p}_2^{-m}{p}_1{p}_2^{m-1}{p}_1^2{p}_2^{-1}{p}_1{p}_2^{-1}{p}_1^{-2}{p}_2^{1-m}{p}_1{p}_2^{m-2}\in ⟨p_1,p_2⟩$$ .

Consider the following permutations:

$$$ \begin{array}{c}{p}_5=p_1^{-m}{p}_3^{-1}{p}_1^m=\left(xy{a}_1\right)\\ p_6=p_2^m{p}_4^{-1}{p}_2^{-m}=\left(yx{a}_m\right)\\ p_7=p_5^{-1}{p}_6{p}_1{p}_2^{-1}=\left(x{a}_1{b}_1\right)\\ p_8\left(k\right)=p_1^{-k}{p}_7^{-1}{p}_1^k\end{array}$$$

When  $$ k$$  isn’t  $$ 0$$  (or a multiple of  $$ m+n+2$$ ), we can generate any 3-cycle  $$ \left(x{a}_{1}z\right)$$  where  $$ z$$  is any element in  $$ A=\{a_2,a_3,...,a_m,y,b_n,...,b_2,b_1\}$$  by considering  $$ \prod _{i=1}^j{p}_8\left(i\right)=\left(x{a}_{1}z\right)$$  where  $$ z$$  is the  $$ j^{tℎ}$$  element of  $$ A$$ . By Proposition 2.9,  $$ \text{Alt}\left(S\right)\le ⟨p_1,p_2⟩$$ .Letting  $$ m\le n$$  without loss of generality, discuss the excluded cases. When  $$ m=0,n\ne 0$$ ,  $$ \left(xy{b}_k\right)=p_2^k{p}_1^{-k}$$  so  $$ \text{Alt}\left(S\right)\le ⟨p_1,p_2⟩$$  by Proposition 2.9. When  $$ m=n=0$$ ,  $$ \text{Alt}\left(S\right)$$  is the identity, which is trivially a subgroup of  $$ ⟨p_1,p_2⟩$$ . When  $$ m=1,n>2$$ , consider  $$ p_3=p_1^2{p}_2^{-2}{p}_1^{-1}{p}_2^3{p}_1^{-2}{p}_2^{-2}{p}_1^2{p}_2{p}_1^{-3}{p}_2^2=\left(x{a}_{1}y\right)$$  and  $$ p_4\left(k\right)=p_1^{-k}{p}_3{p}_1^k$$ . Considering  $$ \prod _{i=0}^j{p}_4\left(i\right)=\left(x{a}_{1}z\right)$$  where  $$ z$$  is the  $$ (j+1{)}^{tℎ}$$  element of  $$ \{y,b_n,...,b_1\}$$  like before, we generate all 3 cycles  $$ \left(a_{1}xz\right)$$  required for Proposition 2.9 to imply that  $$ \text{Alt}\left(S\right)\le ⟨p_1,p_2⟩$$ . When  $$ m=n=1$$ , consider the 3-cycles  $$ p_1^{-1}{p}_2^{-1}=\left(yx{b}_1\right)$$  and  $$ p_1{p}_2=\left(yx{a}_1\right)$$  and use Proposition 2.9 to show that  $$ \text{Alt}\left(S\right)\le ⟨p_1,p_2⟩$$ . When  $$ m=2,n>4$$ , consider  $$ p_3=p_2^{-1}{p}_1^{-2}{p}_2^{-1}{p}_1^{-1}{p}_2^2{p}_1{p}_2^2{p}_1^{-3}{p}_2^{-1}{p}_1^{-1}{p}_2^2{p}_1{p}_2{p}_1=\left(x{a}_2{a}_1\right)$$  and  $$ p_4\left(k\right)=p_1^{-k}{p}_3^{-1}{p}_1^k$$  like before, concluding that  $$ \text{Alt}\left(S\right)\le ⟨p_1,p_2⟩$$ . When  $$ m=2,n=3$$ , consider instead  $$ p_3=p_2{p}_1^{-1}{p}_2^{-2}{p}_1^{-1}{p}_2^{-2}{p}_1^{-1}{p}_2^{-1}{p}_1=\left(x{a}_2{a}_1\right)$$  and proceed as before.We have shown that for all cases in the lemma,  $$ \text{Alt}\left(S\right)\le ⟨p_1,p_2⟩$$ . When  $$ m+n$$  is even, both  $$ p_1$$  and  $$ p_2$$  are even permutations so  $$ \text{Alt}\left(S\right)\ge ⟨p_1,p_2⟩\Rightarrow \text{Alt}\left(S\right)=⟨p_1,p_2⟩$$ . When  $$ m+n$$  is odd, both  $$ p_1$$  and  $$ p_2$$  are odd permutations so  $$ \text{Alt}\left(S\right)\ngeqq ⟨p_1,p_2⟩\Rightarrow \text{Sym}\left(S\right)=⟨p_1,p_2⟩$$ .  □

The permutation group of any theta graph contains such elements  $$ p_1$$  and  $$ p_2$$ . Consider a bipartite theta graph  $$ G$$  that is not (2,2,2) or (2,2,4). Any choice of 2 simple paths from  $$ x$$  to  $$ y$$  must have  $$ m+n$$  even, otherwise a subgraph consisting of the 2 paths is a polygon graph of odd length, which meaning  $$ G$$  is not bipartite. Verify that we can always choose 2 paths  $$ (x,a_1,...,a_m,y)$$  and  $$ (x,b_1,...,b_n,y)$$  satisfying  $$ m+n\text{ even, }\{m,n\}\ne \left\{\mathrm{2,4}\right\},(m,n)\ne \left(\mathrm{2,2}\right)$$ , and assume that  $$ f^{-1}\left(\mathrm{⌀}\right)=c_i$$  for some  $$ i$$  by Proposition 4.6. Defining  $$ p_1$$  and  $$ p_2$$  as before, it follows by Lemma 4.8 that  $$ P_G$$  must contain the permutation group of  $$ S=\{x,a_1,...,a_m,y,b_n,...,b_1\}$$  which is  $$ \text{Alt}\left(S\right)$$ . Since this is an alternating group, it contains the 3-cycles  $$ \left(a_1{a}_{2}k\right)$$  for all  $$ k\in S-\{a_1,a_2\}$$ . We show that  $$ P_G=\text{Alt}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$  by generating the 3-cycles  $$ \left(a_1{a}_{2}k\right)$$  for all  $$ k\in V\left(G\right)-\{a_1,a_2,f^{-1}(\mathrm{⌀}\left)\right\}$$ :Performing a sequence of moves moving the blank label to $$ c_i,c_{i+1},...c_j,y,b_n,...,b_1,x,c_1,...,c_i$$  corresponds to a permutation $$ p_3=(x{b}_1\cdots b_{n}y{c}_j\cdots c_{i+1}{c}_{i-1}\cdots c_1)\in P_G$$ . Conjugating the  $$ 3$$ -cycle  $$ \left(a_1{a}_{2}y\right)$$  by a power of  $$ p_3$$  yields a 3-cycle  $$ \left(a_1{a}_{2}k\right)$$  with  $$ k$$  in the cycle notation of  $$ p_3$$ . Thus, a 3-cycle  $$ \left(a_1{a}_{2}k\right)$$  exists in  $$ P_G$$  for  $$ k\in V\left(G\right)-\{a_1,a_2,f^{-1}(\mathrm{⌀}\left)\right\}$$ , and we can use Proposition 2.9 giving  $$ P_G\ge \text{Alt}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ . We prove the following proposition to show that equality holds:

Proposition 4.9. The puzzle group of a simple finite connected bipartite graph  $$ G$$  must be a subgroup of  $$ \text{Alt}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ .

Proof. Consider any sequence of moves from the solved state to a labeling  $$ f$$  such that  $$ s^{-1}\left(\mathrm{⌀}\right)=f^{-1}\left(\mathrm{⌀}\right)$$ . There must be an even number of moves since the graph is bipartite, corresponding to a permutation in  $$ \text{Sym}\left(V\right(G\left)\right)$$  (containing the empty vertex) which can be written as an even number of transpositions. The resulting permutation must be even and fixes  $$ \mathrm{⌀}$$ , so  $$ P_G$$  must be a subgroup of  $$ \text{Alt}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ .  □

So,  $$ P_G=\text{Alt}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ .Now, consider a non bipartite theta graph graph  $$ G$$  that is not (1,2,2). We can now choose 2 paths  $$ (x,a_1,...,a_m,y)$$  and  $$ (x,b_1,...,b_n,y)$$  satisfying  $$ m+n\text{ odd, }\{m,n\}\ne \left\{\mathrm{1,2}\right\}$$  assuming that  $$ f^{-1}\left(\mathrm{⌀}\right)=c_i$$  for some  $$ i$$ .  $$ P_G$$  contains  $$ \text{Sym}\left(S\right)$$  by Lemma 4.8, so we can find a transposition  $$ \left(a_{1}k\right)\in P_G$$  for  $$ k\in S$$ . Conjugating  $$ \left(a_{1}y\right)$$  by a power of  $$ p_3=(x{b}_1\cdots b_{n}y{c}_j\cdots c_{i+1}{c}_{i-1}\cdots c_1)$$ , we reach every transposition  $$ \left(a_{1}k\right)$$  for  $$ k$$  in the cycle notation of  $$ p_3$$ , and thus every transposition  $$ \left(a_{1}k\right)$$  for  $$ k\in V\left(G\right)-f^{-1}\left(\mathrm{⌀}\right)$$  is in  $$ P_G$$ . This generates the symmetric group  $$ P_G=\text{Sym}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ .

4.3. Considerations for exceptional theta graphs

For the special cases excluded from the above discussion, we discuss each of them individually.

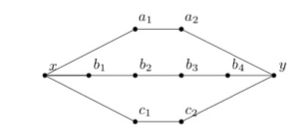
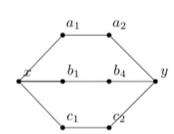
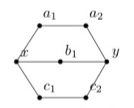
Let  $$ G$$  be the (2,2,2) theta graph shown in Fig. 4.6 and let  $$ f\left(b_2\right)=\mathrm{⌀}$$ . Define the permutations  $$ p_1=\left(y{a}_2{a}_{1}x{b}_1\right)$$ ,  $$ p_2=\left(y{c}_2{c}_{1}x{b}_1\right)$$ , and  $$ p_3=\left(a_2{a}_{1}x{c}_1{c}_2\right)$$ , noting that they are all in  $$ P_G$$ . [4] considered a 3-cycle generated from similar permutations, but we consider an easier way to generate a 3-cycle  $$ p_4=p_1^{-2}{p}_3{p}_1^2{p}_2^{-1}=\left(y{c}_2{c}_1\right)\in P_G$$ . We can now conjugate  $$ p_4$$  by powers of  $$ p_1$$  and use Proposition 2.9 and the fact that  $$ G$$  is bipartite to conclude that  $$ P_G=\text{Alt}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ .Let  $$ G$$  be the (2,2,4) theta graph shown in Fig. 14 and let  $$ f\left(b_4\right)=\mathrm{⌀}$$ . Define  $$ p_1=\left(y{a}_2{a}_{1}x{b}_1{b}_2{b}_3\right)$$ ,  $$ p_2=\left(y{c}_2{c}_{1}x{b}_1{b}_2{b}_3\right)$$ , and  $$ p_3=\left(a_2{a}_{1}x{c}_1{c}_2\right)$$  in  $$ P_G$$ . Consider the 3-cycle  $$ p_4=p_1^{-3}{p}_3^{-1}{p}_2{p}_1^{-2}{p}_2^2=\left(y{c}_2{c}_1\right)$$ . Conjugating by a power of  $$ p_1$$ , we conclude that  $$ P_G=\text{Alt}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ .Let  $$ G$$  be the (1,2,2) theta graph shown in Fig. 15 and let  $$ f\left(b_1\right)=\mathrm{⌀}$$ . Define  $$ p_1=\left(y{a}_2{a}_{1}x\right)$$ ,  $$ p_2=\left(y{c}_2{c}_{1}x\right)$$ ,  $$ p_3=\left(a_2{a}_{1}x{c}_1{c}_2\right)$$ ,  $$ p_4=\left(c_1{c}_{2}y{a}_2{a}_1\right)$$ , and claim that  $$ ⟨p_1,p_2,p_3,p_4⟩$$  contains all permutations corresponding to a sequence of moves fixing the position of the blank label. Consider an arbitrary sequence of moves represented by a sequence of positions of the blank label. Assume that this sequence never ’backtracks on itself’, i.e. there is no consecutive  $$ a,b,a$$  in the sequence for 2 vertices  $$ a,b$$ . This is reasonable since canceling the  $$ b,a$$  has no effect on the permutation of labels. Split this sequence of positions for every instance of  $$ b_1$$  not at the beginning or end. Each subsequence must correspond to  $$ p_1$$  or its inverse,  $$ p_2$$  or its inverse, a power of  $$ p_3$$ , or a power of  $$ p_4$$ . So the above claim is true.Now, consider the permutation  $$ p_5=p_2^{-1}{p}_1{p}_2^{-1}{p}_1^2=\left(a_2{c}_2\right)\left(a_{1}x\right)\left(c_{1}y\right)$$ . We claim that this, along with  $$ p_3$$  generate a transitive subgroup of  $$ S_6$$  isomorphic to  $$ S_5$$  with the following proposition:

Proposition 4.10. The subgroup  $$ H=⟨\left(15\right)\left(23\right)\left(46\right),\left(12345\right)⟩<S_6$$  is isomorphic to  $$ S_5$$ .

[4]constructed this group by considering the action of the group of linear fractional transformations  $$ {\text{PGL}}_2\left({\mathbb{F}}_5\right)$$  on the set  $$ {\mathbb{F}}_5\cup \mathrm{\infty }$$ . We follow the construction in [6] instead:

Proof. Consider all the subgroups of  $$ S_5$$  with order 5:

$$$ \begin{array}{c}{P}_1=⟨\left(12345\right)⟩\\ P_2=⟨\left(12354\right)⟩\\ P_3=⟨\left(12453\right)⟩\\ P_4=⟨\left(12534\right)⟩\\ P_5=⟨\left(12435\right)⟩\\ P_6=⟨\left(12543\right)⟩\end{array}$$$

These are all the Sylow 5-subgroups of  $$ S_5$$ , since no subgroups of order  $$ 25$$  exist by Lagrange’s theorem. By the Second Sylow theorem, there exists an element  $$ g\in S_5$$  with  $$ g^{-1}{P}_{i}g=P_j$$  for any  $$ i,j$$ , meaning  $$ S_5$$  can act transitively on the set  $$ X$$  of Sylow 5-subgroups by conjugation. Consider the homomorphism from this group action  $$ f:S_5\mapsto S_6$$ . The kernel of  $$ f$$  must be normal, so it is isomorphic to  $$ S_5$$ ,  $$ A_5$$ , or the trivial subgroup.  $$ \text{Im}\left(f\right)$$  must be a transitive subgroup of  $$ S_6$$ , so it has order at least 6. By the first isomorphism theorem,  $$ \left|S_5\right|=\left|\text{ker}\right(f\left)\right|\left|\text{Im}\right(f\left)\right|$$ , so it follows that  $$ \left|\text{ker}\right(f\left)\right|\le 20\Rightarrow \text{ker}\left(f\right)\text{ is trivial}$$ . So the isomorphism from  $$ S_5/\text{ker}\left(f\right)$$  to  $$ \text{Im}\left(f\right)$$  is an isomorphism between  $$ S_5$$  and  $$ \text{Im}\left(f\right)$$ .We show now that  $$ \text{Im}\left(f\right)=H$$ . The generator  $$ \left(12345\right)\in S_6$$  corresponds to an element  $$ g=\left(12543\right)\in S_5$$  satisfying  $$ g^{-1}{P}_{1}g=P_2,g^{-1}{P}_{2}g=P_3,g^{-1}{P}_{3}g=P_4,g^{-1}{P}_{4}g=P_5,g^{-1}{P}_{5}g=P_1,g^{-1}{P}_{6}g=P_6$$ , so  $$ \left(12345\right)\in \text{Im}\left(f\right)$$ . The generator  $$ \left(15\right)\left(23\right)\left(46\right)\in S_6$$  corresponds to an element  $$ g=\left(34\right)\in S_5$$  satisfying  $$ g^{-1}{P}_{1}g=P_5,g^{-1}{P}_{2}g=P_3,g^{-1}{P}_{3}g=P_2,g^{-1}{P}_{4}g=P_6,g^{-1}{P}_{5}g=P_1,g^{-1}{P}_{6}g=P_4$$ , so  $$ \left(15\right)\left(23\right)\left(46\right)\in \text{Im}\left(f\right)$$ . So,  $$ H\le \text{Im}\left(f\right)$$ . But the elements  $$ \left(12543\right)$$  and  $$ \left(34\right)$$  generate  $$ S_5$$ , so the elements  $$ \left(12345\right)$$  and  $$ \left(15\right)\left(23\right)\left(46\right)$$  generate  $$ \text{Im}\left(f\right)$$ , meaning  $$ H\ge \text{Im}\left(f\right)\Rightarrow H=\text{Im}\left(f\right)$$ .  □

We show that  $$ p_1,p_2,p_4\in ⟨p_3,p_5⟩$$ :

$$$ \begin{array}{ccc}{p}_2& =p_5{p}_3{p}_5{p}_3^2{p}_5{p}_3^3& \in ⟨p_3,p_5⟩\\ p_1& =p_2^2{p}_5^{-1}{p}_2^{-2}& \in ⟨p_3,p_5⟩\\ p_4& =p_2{p}_5{p}_2^{-1}& \in ⟨p_3,p_5⟩\end{array}$$$

So,  $$ P_G=⟨p_3,p_5⟩\cong S_5$$ . Since this group is transitive,  $$ G$$  is a transitive subgroup of  $$ S_6$$  isomorphic to  $$ S_5$$ .

4.4. Inducting on the cyclomatic number

We complete the proof of Theorem 4.7 by inducting on the cyclomatic number  $$ \left|E\right(G\left)\right|-\left|V\right(G\left)\right|+1$$ , discussing bipartite and non-bipartite graphs separately. We prove the following theorem, first introduced in [7], to help with induction:

Theorem 4.11. Let  $$ G$$  be a simple finite non-separable graph and denote its cyclomatic number by  $$ \beta \left(G\right)\ge 2$$ . Suppose that  $$ H$$  is a non-separable proper subgraph of  $$ G$$  with cyclomatic number  $$ \beta \left(G\right)-1$$ . Then we can write  $$ G=H\cup A$$ , where  $$ A$$  is a subgraph of  $$ G$$  with cyclomatic number 0 and  $$ H\cap A$$  consists only of the ends of A.

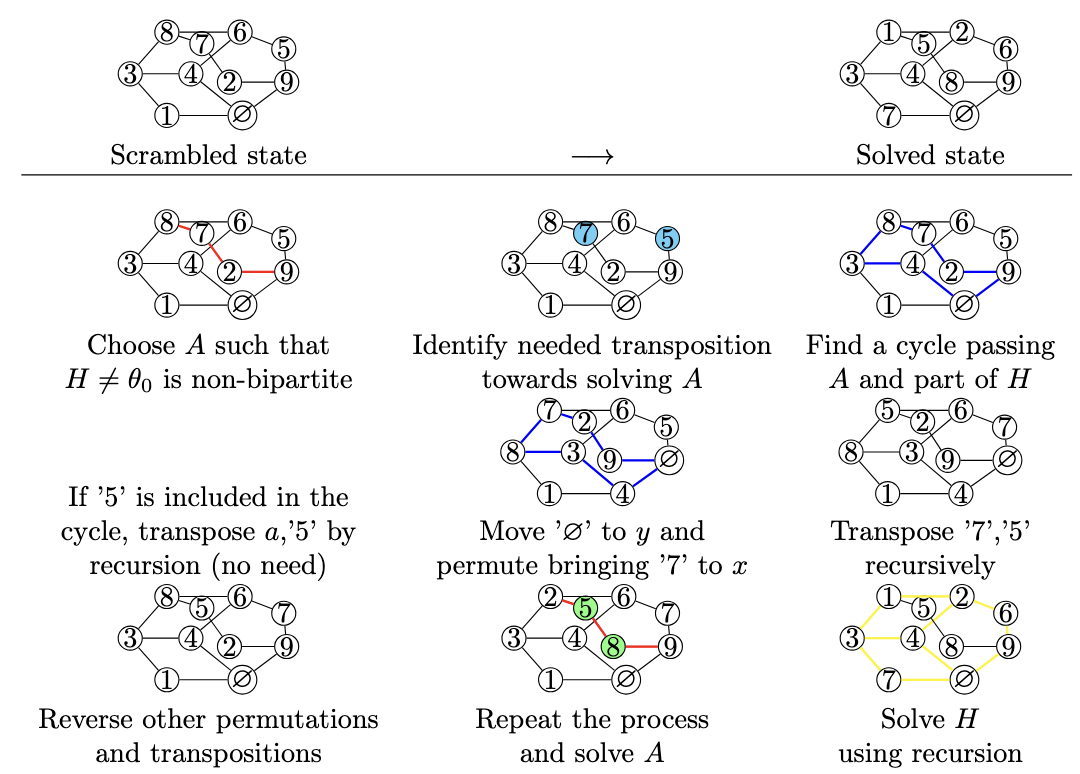
Proof. Take any subgraph  $$ H$$  satisfying the properties in the theorem, and let  $$ n$$  be the number of vertices in  $$ G$$  but not in  $$ H$$ . Since  $$ H$$  has cyclomatic number  $$ \beta \left(G\right)-1$$ , the number of edges in  $$ G$$  but not in  $$ H$$  must be  $$ n+1$$ . Since  $$ G$$  is non-separable, the edges and vertices not in  $$ H$$  must connect to at least 2 vertices in  $$ H$$ . Let  $$ A$$  include the edges and vertices not in  $$ H$$ , and the vertices in  $$ H$$  connected to an edge not in  $$ H$$ . Since  $$ A$$  must have cyclomatic number 0, it must be possible to obtain  $$ A$$  from subdivisions of the graph below:

Since  $$ G$$  is non-separable, the ends of this graph must be in  $$ H$$ . If any other vertices in  $$ A$$  are in  $$ H$$ , the cyclomatic number of  $$ G$$  increases by 1, making  $$ H$$  have cyclomatic number  $$ \beta \left(G\right)-2$$ . So, we can write  $$ G=H\cup A$$  where  $$ H\cap A$$  consists only of the ends of A.  □

We now begin the induction, constructing explicitly the permutations required to generate the puzzle group, without relying on the doubly transitive property of  $$ P_G$$  used in [4] and [8].The bipartite case: Having proven that Theorem 4.7 is true for bipartite non-separable graphs with cyclomatic number 2 (which are the theta graphs), we assume that Theorem 4.7 is true for bipartite non-separable graphs with cyclomatic number  $$ k\ge 2$$ . Take an arbitrary bipartite non-separable graph of cyclomatic number  $$ k+1$$  and write  $$ G=H\cup A$$  by Theorem 4.11, creating a bipartite graph  $$ H$$  of cyclomatic number  $$ k$$  whose puzzle group is  $$ P_H=\text{Alt}\left(V\right(H)-f^{-1}(\mathrm{⌀}\left)\right)$$ . Since this graph is bipartite, by Proposition 4.9,  $$ P_H$$  is a subgroup of  $$ \text{Alt}\left(V\right(H)-f^{-1}(\mathrm{⌀}\left)\right)$$  and  $$ P_G$$  does not contain  $$ \text{Sym}\left(V\right(H)-f^{-1}(\mathrm{⌀}\left)\right)$$ . Letting  $$ x$$  and  $$ y$$  be the ends of  $$ A$$ , let the simple path from  $$ x$$  to  $$ y$$  in  $$ A$$  pass through vertices  $$ k_1,k_2,...,k_m$$ , and find a simple path from  $$ y$$  to  $$ x$$  in  $$ H$$  that do not pass through some  $$ a_1,a_2$$  in  $$ H$$ , letting it pass through vertices  $$ v_1,v_2,...,v_n$$  (One can verify that this is always possible). Assuming  $$ f\left(\mathrm{⌀}\right)=y$$  by Proposition 4.6, we can move the blank space to vertices  $$ k_m,...,k_1,x,v_n,...,v_1,y$$  to create a permutation  $$ p=(v_1{v}_2\cdots v_{n}x{k}_1{k}_2\cdots k_n)\in P_G$$ . Conjugating the 3-cycle  $$ \left(a_1{a}_{2}x\right)$$  by a power of  $$ p$$  can create all 3-cycles  $$ \left(a_1{a}_{2}k\right)$$  for  $$ k\in A$$ . Together with the fact that  $$ P_H=\text{Alt}\left(V\right(H)-f^{-1}(\mathrm{⌀}\left)\right)$$  and by Proposition 2.9 and Proposition 4.9,  $$ P_G=\text{Alt}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ .The non-bipartite case: Ensure first that given a graph with cyclomatic number 3 containing a subgraph  $$ {\theta }_0$$ , that we can always write  $$ G=H\cup A$$  where  $$ H$$  a non-bipartite graph that is not  $$ {\theta }_0$$ . Consider all such possible types of graphs, highlighting in red components in  $$ G$$  that are not in  $$ H$$, and highlighting in blue the components (possibly and sometimes necessarily subdivided) that could have been removed to yield   

H=θ0. The below consideration is omitted in [4] and partially omitted in [8]:

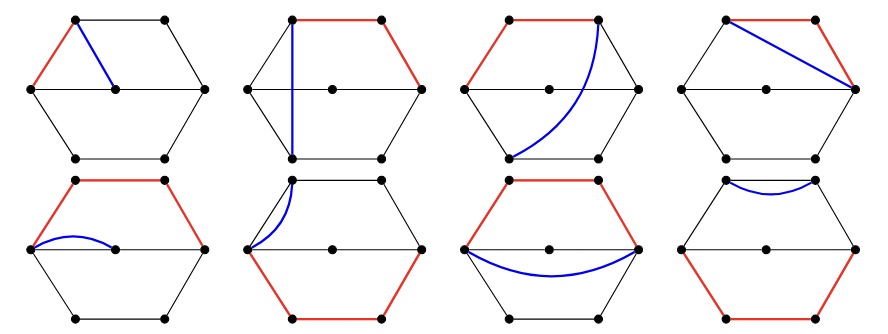
Assume that Theorem 4.7 is true for non-bipartite non-separable graphs with cyclomatic number  $$ k\ge 2$$ . Take an arbitrary non-bipartite non-separable graph  $$ G$$  with cyclomatic number  $$ k+1$$  and we can always write  $$ G=H\cup A$$  where  $$ H$$  is a non-bipartite graph of cyclomatic number  $$ k$$  whose puzzle group is  $$ P_H=\text{Sym}\left(V\right(H)-f^{-1}(\mathrm{⌀}\left)\right)$$  (Since  $$ H\ne {\theta }_0$$ ). Letting  $$ x$$  and  $$ y$$  be the ends of  $$ A$$ , let the path from  $$ x$$  to  $$ y$$  in  $$ A$$  pass through vertices  $$ k_1,k_2,...,k_m$$ , and find a path from  $$ y$$  to  $$ x$$  in  $$ H$$  that do not pass through some  $$ a\in H$$ , letting it pass through vertices  $$ v_1,v_2,...,v_n$$  (One can verify that this is always possible). As before, we can create a permutation  $$ p=(v_1{v}_2\cdots v_{n}x{k}_1{k}_2\cdots k_n)\in P_G$$ . Conjugating the transposition  $$ \left(ax\right)$$  by a power of  $$ p$$  can create all transpositions  $$ \left(ak\right)$$  for  $$ k\in A$$  which, together with the fact that  $$ P_H=\text{Sym}\left(V\right(H)-f^{-1}(\mathrm{⌀}\left)\right)$$ , generate the symmetric group  $$ P_G=\text{Sym}\left(V\right(G)-f^{-1}(\mathrm{⌀}\left)\right)$$ .Theorem 4.7 is now proved.

5. Extensions of Wilson’s theorem

In this section, we extend Theorem 4.7 to 1-connected, disconnected graphs, and polygon graphs. This consideration has already been made by [7] on another theorem in [2], and [10] considered the one-connected case without proof. We give a new brief proof of Theorem 5.1 in this section, an extension of Theorem 4.7:

Theorem 5.1. Let  $$ G$$  be a finite simple graph. If  $$ G\ne {\theta }_0$$  is a non-separable graph that is not a polygon,  $$ P_G=\text{sym}\left(V\right(G)-\{f^{-1}\left(\mathrm{⌀}\right)\left\}\right)$$ , unless  $$ G$$  is bipartite, in which case  $$ P_G=\text{alt}\left(V\right(G)-\{f^{-1}\left(\mathrm{⌀}\right)\left\}\right)$$ . If  $$ G={\theta }_0$$ , then  $$ P_G\subset \text{sym}\left(V\right(G)-\{f^{-1}\left(\mathrm{⌀}\right)\left\}\right)$$  is a transitive subgroup of  $$ S_6$$  isomorphic to  $$ S_5$$ . If  $$ G$$  is a polygon,  $$ P_G\subset \text{sym}\left(V\right(G)-\{f^{-1}\left(\mathrm{⌀}\right)\left\}\right)$$  is isomorphic to the cyclic group  $$ {\mathbb{\mathbb{Z}}}_{n-1}$$ . If  $$ G$$  is 1-connected (separable and connected) with non-separable components  $$ H_i$$ ,  $$ P_G$$  is the direct product  $$ \prod _i{P}_{G_i}$$ , where  $$ G_i$$  is a non-separable component of  $$ G$$ . If  $$ G$$  is disconnected,  $$ P_G$$  is the puzzle group of the connected component containing  $$ f^{-1}\left(\mathrm{⌀}\right)$$ .