1. Introduction

The rapid development of big data analysis technology makes people urgently require to mine more valuable information from big data, and the first step of mining is to have enough public data. However, at present, large data owners such as hospitals, governments, and big data companies that have a large amount of data will inevitably involve citizens' privacy issues when disclosing relevant data.

A traditional paradigm for (combinatorial) data privacy entails making a matrix k-anonymous, meaning that each row must appear at least k times [1][2]. The equally extremely popular "differential privacy" model, which has a statistical rather than combinatorial flavor, is not discussed in this study[3]. It is commonly recognized that the k-anonymity notion has some flaws, such as when the anonymized data is used repeatedly [1]. Due to its simplicity and good interpretability, this paper will focus on k-anonymity. The notion behind k-anonymity is that each row of the matrix symbolizes a different person, and the associated row's k-fold appearance prevents situations where the person or thing behind can be recognized. It is obvious that some information loss, or the suppression of some matrix entries, must be accepted in order to achieve this goal (blanked out). In this method, details about specific traits (represented by the matrix's columns) are lost. Thus, when converting an arbitrary data matrix into a k-anonymous one, it makes sense to try to limit this information loss. Even in special circumstances, the associated optimization problem, k-ANONYMITY, is difficult to approximate and NP-hard [4–8]. To make a matrix k-anonymous, it largely relied on heuristic methods; yet, it played a vital part in many applications [2][9][10]. The "usefulness" (also in terms of expressiveness) of the anonymized data was discovered to require caution [11][12].

In this paper, the whole dataset is divided into some large clusters by clustering algorithm, and then the greedy algorithm is applied to these divided clusters to K-anonymize them.

In the future, such as medical systems, transportation hub, shopping website traffic platform informatization construction and its application in business surveys and the need of scientific research, a large number of user data collection or real-time grabbing and surveyed sharing released within a certain range, although the data included in the user to interact with platform of legal information necessary, but it also contains many personal privacy information, Information sharing is inevitable. In order to ensure the effectiveness of information and avoid the disclosure of personal privacy, it is necessary to obfuscate the information in advance and hide some unnecessary information through the methods described in this article.

2. Materials and methods

2.1. Modeling ideas and formulas

The global optimum is approximated by finding the local optimum. Each time, the smallest hiding distance is selected, and its data is merged into a new data ○1, and then the hiding distance between data ○1 and other data is calculated. This process is repeated, and finally every data exists in the data group, that is, there is no independent data.

• there is no hiding spot data tuple calculation formula of the hidden distance between:

\( distance({t_{i}},{t_{j}})=\sum _{{k_{i}}{∈t_{i}},{k_{j}}ϵ{t_{j}}}2×δ({k_{i}},{k_{j}}) \) (1)

If different, output 1, otherwise output 0, and the distance is the total number of times two data tuples need to change into the same form.

\( δ({k_{i}},{k_{j}})=\begin{cases} \begin{array}{c} 0，{k_{i}}={k_{j}} \\ 1，{k_{i}}≠{k_{j}} \end{array} \end{cases} \) (2)

• Calculation formula of hidden distance between data tuples and equivalent data groups

\( distance({t_{i}},{ec_{j}})=distance({t_{i}},{t^{*}})+{w_{j}}×distance({ec_{j}},{t^{*}}) \) (3)

The 𝑡𝑖 for the data tuple, 𝑒𝑐𝑗 for the equivalent data set, 𝑤𝑗 as the hidden distance weighting, 𝑡∗ for 𝑡𝑖 with 𝑒𝑐𝑗 after optimizing the equivalent data set.

\( {w_{j}}=|{ec_{j}}|×α \) (4)

The \( |{ec_{j}}| \) for the equivalent data in data set the number of tuples, 𝛼 for setting adjustment coefficient, 𝛼 selection will affect the calculate method of constructing the number of tuples in the equivalent data set.

• the hidden distance formula between the equivalent data set

\( distance({ec_{i}},{ec_{j}})=distance({ec_{i}},{t^{*}})+{w_{j}}×distance({ec_{j}},{t^{*}}) \) (5)

The \( { ec_{i}} \) with \( {ec_{j}} \) for the two equivalent data set.

2.2. Symbol description

2.3. Process

Data input: contain 𝑛 record table data, parameter p values

Output: k after the anonymous form

Step 1: Calculate the distances between data tuples or equivalent data groups in the data table to obtain the lower triangular moment matrix for storing the distances.

Step 2: Select the element with the smallest value in the distance matrix and merge the data tuples or equivalent data groups represented by its rows and columns into a new cluster.

Step 3: Perform the optimal hiding processing on the current cluster to form an undifferentiated equivalent group, and bring the modified hidden data into the data table to update the distance matrix.

Step 4: Repeat steps 1, 2, and 3 until each individual is in an undifferentiated equivalent data group.

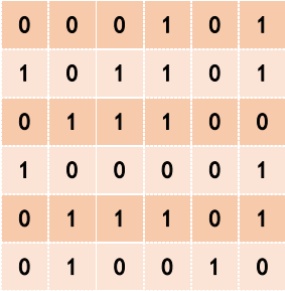
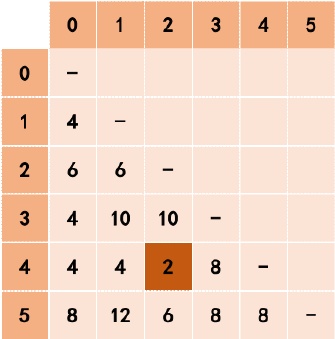
Figure 1. Distance matrix update process.

3. Result

It demonstrated that the greedy heuristic outperforms the optimal solution generated by the ILP implementation in three scenarios using real-world datasets in terms of solution quality. Although the heuristic in this study is significantly more efficient than the exact technique, the results are still rather close to the optimum and in many situations, they were optimal (the ILP was, on average, more than 1000 times slower). With a higher degree k of anonymity, the heuristic findings tend to be closer to the ideal number of suppressions

Figure 2. The amount of data lost in a data table.

4. Discussion

4.1. Advantages of the model

The solution method of this model is universal and simple, and can be applied to solve high-dimensional data sets and large data sets. In dealing with the large data set with high dimension 𝑝 - heavy protection problems, still can draw better data anonymous.

Hybrid clustering greedy model has good expansibility. For high dimension, large amount of data sets, under appropriate 𝑘 clustering parameters value, can at the same time of stable data loss, sharply reduce operation time; Also, for low dimensional degree, amount of data on small data sets, increasing the clustering parameters 𝑘 values, the better the results of the data hiding can be.

4.2. Model shortcomings

Due to the limitation of the greedy algorithm, the model results only in the distance parameter 𝛼 situation of the local optimal solution, and is not the global optimal solution, and to a large amount of data calculation, the calculation takes too long.

5. Conclusion

This research introduces the clustering algorithm K-𝑚𝑜𝑑𝑒, combined with the density-based initial point selection method, combining the hybrid clustering algorithm with the greedy algorithm, and propose a data hiding method based on the clustering and the greedy algorithm.

This result fits both hypotheses perfectly: 1. Different data refers to differences, and the case that multiple data are in the same state is not considered. 2. Assume that the local optimum is taken several times, and the final result is the global optimum.

Future work will focus on creating practical algorithms for the general k-anonymity problem using the theoretical findings from this study. More particularly, it entails connecting and transforming the Restricted k-anonymity problem and the general k-anonymity problem in order to produce a new, efficient exact method and provide a superior approximate algorithm scheme.

We have fulfilled a number of unresolved issues on the subject by proving the hardness and viability of numerous strategies employed in database privacy. The conclusion is that, even in highly special instances, the majority of these problems are challenging to answer optimally; nevertheless, in some fascinating cases, these problems can be handled more quickly. Several intriguing unanswered problems explore potential workarounds for this intractability:

• -How close can the difficult problems be to being solved? The best known approximation approach for k-anonymity, presented by Park and Shim [13], for instance, only suppresses O(log k) times the ideal number of entries. When there are less attributes, may approximation ratios be improved?

• -The best known running time for Simplex Matching is O( \( {n^{3}}+{n^{2}}{m^{2}} \) ) steps [14]. Here, the number of nodes in the hypergraph is n, and the number of hyperedges is m. Because the author included a hyperedge for each triple, the procedure for 2-anonymity in this study uses n, which is also the number of database rows, whereas m = \( (\frac{n}{3}) \) = O( \( {n^{3}} \) ). As a result, the algorithm used in this paper for 2-Anonymity has a running time of O( \( {n^{8}} \) ). Is it possible to lower this exponent to a more usable running time?

This research is only theoretical at this point. It is now clearer how structural characteristics of the data matrices may affect the computational complexity of the generally NP-hard data anonymization problems explored here, but it is still not apparent whether some of the proposed solutions would be applicable in real-world settings. However, it is obvious that further reducing exponential factors.

Acknowledgment

I would like to thank professor Venkatesan Guruswami and teacher assistant, for their great support in doing implements and experiments. I’m grateful to anonymous reviewers of algorithms for constructive and extremely fast feedback.