1. Introduction

The rapid proliferation of deep learning (DL) has revolutionized artificial intelligence, enabling breakthroughs in computer vision [1], natural language processing, and autonomous systems. Convolutional Neural Networks (CNNs), such as AlexNet and VGG, pioneered large-scale image recognition but demanded substantial computational resources, limiting their deployment in resource-constrained environments. Subsequent architectures like ResNet [1] introduced residual learning to mitigate vanishing gradients in deeper networks, while DenseNet [2] enhanced feature reuse through dense connectivity. These "big" models achieved state-of-the-art accuracy but incurred high parameter counts and computational costs (e.g., DenseNet161: 28.68M parameters, 7.79G operations [2]), rendering them impractical for embedded platforms.

In response, lightweight "little" models like MobileNetV2 [3] and ShuffleNet V2 [4] emerged, optimizing for efficiency through inverted residuals, channel shuffling, and aggressive parameter reduction. For instance, ShuffleNet V2 x0.5 utilizes only 1.37M parameters and 42.52M operations [4]. However, Table 1 reveals a critical trade-off: while these models reduce compute intensity, they exhibit severe accuracy degradation under lower-precision arithmetic—essential for embedded hardware acceleration. ShuffleNet variants suffer catastrophic drops (>65%) in fp16/int8 precision (e.g., ShuffleNet V2 x1.5: 80.91% fp32 vs. 10.03% fp16 [4]), contrasting sharply with robust models like ResNet50 (merely 0.24% int8 loss [2]).

Embedded AI deployments—drones, mobile robots, and smartphones—face stringent constraints: limited memory, energy budgets, and real-time latency requirements. High-parameter models (e.g., ResNet152: 60.19M parameters [2]) exhaust memory bandwidth, while intensive computations (e.g., Dense-Net201: 4.34G ops [1]) drain batteries and violate latency thresholds. Lower-precision inference (fp16/int8) alleviates these issues but amplifies accuracy volatility, as Table 1 quantifies. Such instability jeopardizes safety-critical applications; a drone’s navigation system failing due to quantization errors could have dire consequences.

To bridge this gap, three key optimization paradigms have evolved:

• Pruning

Pruning is a fundamental model compression technique that eliminates redundant parameters or structural components from neural networks, significantly reducing computational complexity and memory footprint [6]. The objective of Model Pruning is to remove nodes and connections that contribute very little to the model’s output.The pruned model can be significantly smaller than the full model, making it faster and much cheaper for inference,while using less energy.

• Quantization

Quantization reduces the bit-width of weights and activations in deep neural networks (DNNs), enabling efficient deployment on resource-constrained edge de-vices. It maps full-precision (FP32) values to low-bit integers (e.g., INT8), significantly compressing model size and accelerating inference.

• Dynamic inference

Different from conventional deep learning models with fixed computational graphs and parameters during inference, dynamic networks can adjust their structures and parameters in response to varying inputs, resulting in significant advantages regarding accuracy, computational efficiency, adaptability and more [7].

This work analyzes these techniques, evaluating their efficacy in mitigating the embedded deployment challenges highlighted by Table 1. We dissect algorithmic principles, trade-offs, and real-world applicability, setting the stage for a comprehensive discussion on optimizing DL for the embedded frontier.

2. Model optimization techniques

2.1. Pruning

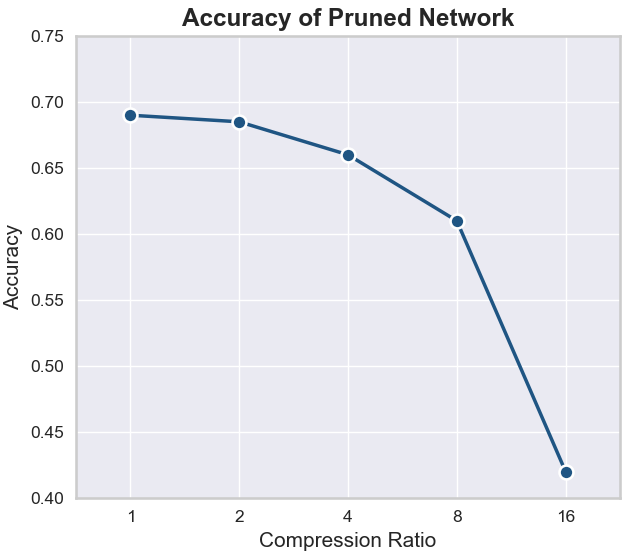
Pruning is a critical model optimization technique aimed at enhancing the efficiency of neural networks while minimizing any degradation in quality. The primary objective is to maximize efficiency quantified through metrics such as FLOPs and compression ratio with the least possible reduction in accuracy [8]. As shown in Figure 1, which plots the accuracy of a pruned network against compression ratio, a compression ratio of 2 results in only a marginal accuracy drop. Beyond this point, higher compression ratios incur severe accuracy penalties. This demonstrates that pruning can achieve substantial efficiency improvements, such as reduced computational cost and model size, with negligible impact on performance, aligning well with the goal of embedded AI systems where resource constraints are paramount.

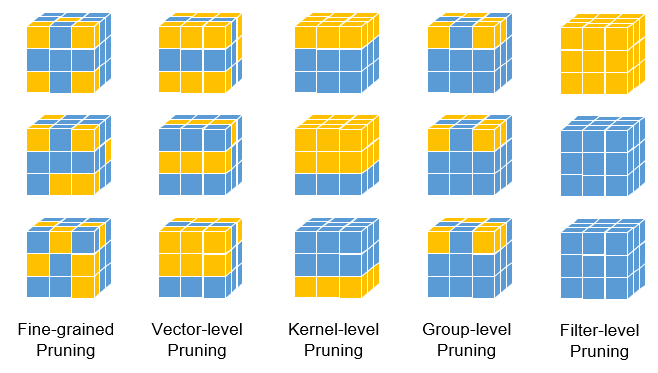
Pruning techniques can be broadly classified into hardware-amenable and hardware-oblivious approaches, based on their compatibility with existing hardware platforms. Hardware-amenable pruning refers to methods that can be directly executed on general-purpose hardware like GPUs, whereas hardware-oblivious pruning necessitates specialized accelerators due to irregular memory access patterns. The distinction largely depends on the granularity and manner of parameter removal, as depicted in Figure 2 [9]. For hardware-oblivious solutions, such as fine-grained pruning, key advantages include a highly controllable compression rate, ease of implementation based on parameter ranking, and the potential to achieve extremely compact models. However, these methods suffer from significant drawbacks: they require specialized hardware and software libraries for deployment, exhibit unpredictable accuracy drops, and often involve tedious, aimless fine-tuning processes to recover performance, making them less practical for standard embedded environments without custom infrastructure [10-13].

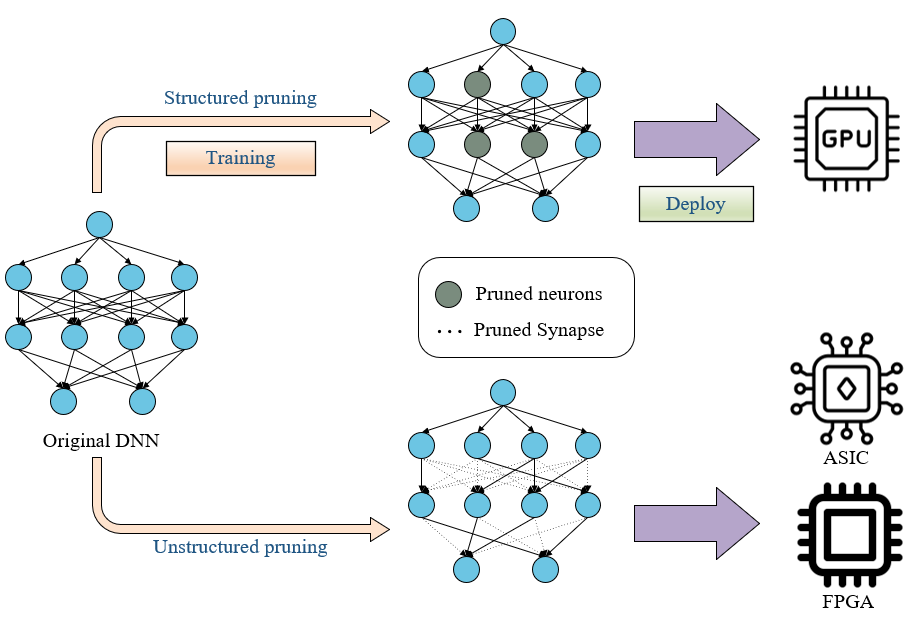
The application of pruning varies significantly across hardware architectures, with structured pruning formally denoting hardware-amenable approaches and unstructured pruning representing hardware-oblivious ones. Structured pruning, which removes entire neurons or filters in a regular pattern, is optimized for deployment on GPUs, leveraging their parallel processing capabilities [14-17]. In contrast, unstructured pruning, characterized by irregular weight removal, is suited for specialized hardware like ASICs and FPGAs, as visualized in Figure 3. This figure highlights how structured pruning focuses on pruned neurons for GPU execution, while unstructured pruning targets pruned synapses for implementation on accelerators, ensuring that embedded AI systems can achieve tailored efficiency gains based on the target hardware platform.

2.2. Quantization

Quantization, a fundamental model optimization technique, reduces the precision of neural network parameters and activations from floating-point representations (e.g., 32-bit) to lower-bit integers (e.g., 8-bit or 4-bit). This approach significantly accelerates on-device inference for embedded AI systems by minimizing computational latency, reducing energy consumption, and decreasing storage requirements—crucial for resource-constrained devices like mobiles and IoT sensors. It also enables efficient deployment on specialized hardware and GPUs by simplifying arithmetic operations. While the core goal is maintaining high accuracy alongside substantial efficiency gains in inference time, power usage, and model size, quantization methods vary: data-free quantization transforms weights/activations using only model-derived statistics (e.g., min-max ranges), offering simplicity but potential accuracy loss; calibration-based methods use small datasets to adjust quantization parameters (e.g., via entropy minimization), improving accuracy at the cost of dataset dependence; and finetune-based quantization incorporates error simulation during training (e.g., using straight-through estimators), allowing weight adjustments for robustness but increasing training complexity [18-22].

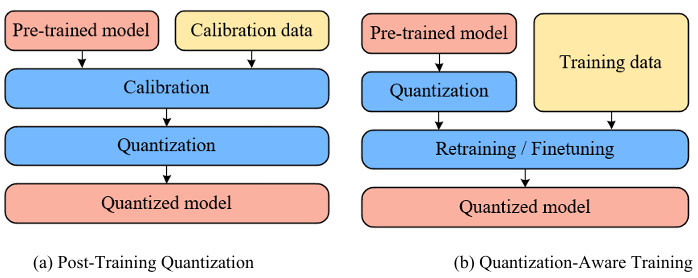
Quantization is further categorized by application stage: post-training quantization (PTQ) and quantization-aware training (QAT), with distinct workflows shown in Figure 4 (a) and Figure 4 (b) respectively. PTQ is applied after full-precision training, converting weights and activations directly to low precision; it typically uses a small calibration dataset to determine quantization parameters (e.g., via min-max or entropy methods) before final quantization [23-26]. This approach is computationally efficient, avoiding retraining overhead, but may incur accuracy loss due to unmodeled quantization effects during initial training. In contrast, QAT integrates quantization simulation during fine-tuning or retraining: starting from a pretrained model and using training data, it inserts fake quantization operators during the forward pass to mimic precision loss while computing gradients in full precision to iteratively adjust weights via backpropagation [27]. This co-optimization significantly enhances robustness to quantization, yielding higher accuracy than PTQ at the cost of substantial training resources and time [28,29]. Consequently, PTQ suits scenarios prioritizing rapid deployment with acceptable accuracy trade-offs, while QAT is preferred for applications demanding maximal precision in re-source-constrained systems.

2.3. Dynamic inference

Dynamic inference, also referred to as dynamic networks, is a model optimization technique that selectively skips redundant computations during inference based on the characteristics of input data, thereby enabling adaptive and efficient processing. This approach, often termed "dynamic inference," reduces computational overhead, latency, and energy consumption which critical for embedded AI systems with limited resources by avoiding unnecessary operations for simpler inputs while maintaining accuracy for complex ones. Dynamic inference represents a paradigm shift from static computational graphs by enabling neural networks to adapt their inference pathways in real-time based on input characteristics. This approach optimizes computational efficiency while maintaining accuracy through three primary mechanisms: sample-wise, spatial-wise, and temporal-wise adaptation.

2.3.1. Sample-wise dynamic inference

Sample-wise methods allocate computation per input sample, Dynamically adjusting network depth or width. The most common dynamic architecture is the early-exit network (Fig. 5), which has multiple intermediate classifiers attached to various internal layers [30-32]. The forward propagation can be halted when adequate confidence is achieved or when specific criteria are met at an internal classifier.

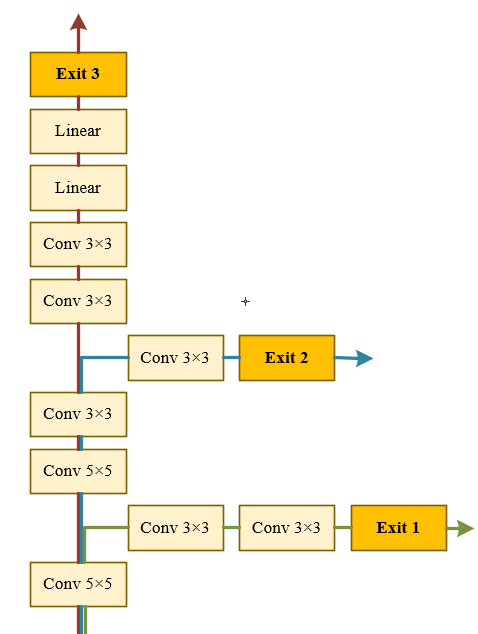
2.3.2. Spatial-wise dynamic inference

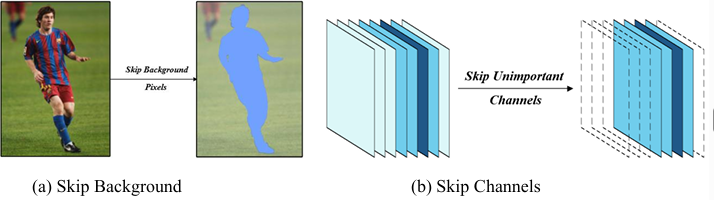
Spatial adaptation focuses on pixel or region-level efficiency. In convolutional layers, dynamic inference can be applied spatially by skipping computations on background pixels that contribute minimally to the output [33-35].For instance, Figure 6(a) demonstrates this spatial skipping, where non-salient regions are bypassed during convolution, focusing computation only on relevant areas to accelerate processing. Methods like Dynamic Convolutions [36-38] skip computations on less informative pixels using predicted spatial masks. For example, entropy-based masking achieves 2.5× speedup in semantic segmentation by processing only 40% of pixels [39].

Similarly, in the channel dimension, as shown in Figure 6(b), dynamic inference skips entire channels with low impact on the final result, such as those with negligible activation magnitudes, to reduce the number of operations per layer [40].

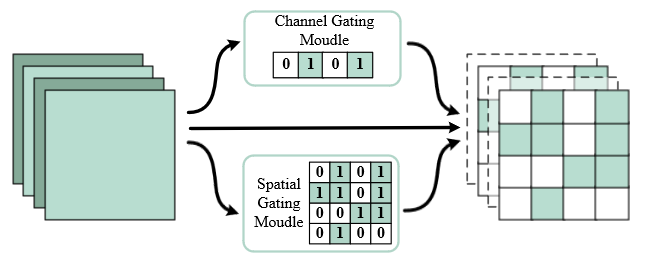
These approaches can be combined for enhanced efficiency. Figure 7 depicts a unified method named Dynamic Dual Gating [41], a dynamic computing method, to reduce the model complexity at run-time. For each convolutional block, dual gating identifies the informative features along two separate dimensions, spatial and channel. Specifically, the spatial gating module estimates which areas are essential, and the channel gating module predicts the salient channels that contribute more to the results. Then the computation of both unimportant regions and irrelevant channels can be skipped dynamically during inference.

2.3.3. Temporal-wise dynamic inference

Temporal-wise dynamic neural networks can unevenly allocate computation along the temporal dimension for sequential data, such as videos or time series data [42]. In the case of streaming data, such as videos, there is typically high correlation among nearby frames. Consequently, the dynamic focus on specific key frames is a crucial characteristic for deep learning models to reduce redundant computation [43].Furthermore, temporal-wise and spatial-wise adaptive computation could be implemented simultaneously to achieve higher efficiency [44].

3. Discussion

3.1. Experimental configuration

All experiments were rigorously designed to evaluate optimization techniques under resource-constrained conditions. The CIFAR-10 dataset, comprising 60,000 32×32 RGB images across 10 classes, served as the primary testbed for quantization and pruning analyses. For dynamic inference validation, we utilized the ImageNet-1k benchmark with 1.28 million training images spanning 1,000 object categories. Hardware execution was conducted on an NVIDIA TU102 GPU (24GB GDDR6 VRAM, 4,608 CUDA cores), leveraging TensorRT 8.6 for accelerated FP16/INT8 operations and cuDNN 8.9 for optimized kernel execution.

Prior to training, standardized preprocessing pipelines were implemented. For CIFAR-10, input images underwent normalization with per-channel mean and standard deviation, supplemented by random horizontal flipping and 32×32 center cropping. ImageNet samples were resized to 256×256 resolution followed by 224×224 center cropping. Quantization deployments employed TensorRT’s post-training quantization workflow, where activation ranges were calibrated using 1,000 randomly selected test images through entropy minimization. Pruning experiments adopted gradual magnitude-based scheduling during fine-tuning, initializing from pre-trained FP32 checkpoints and applying sparsity ramping from 0% to 60% over 10 epochs.

3.2. Comparative analysis of individual optimization techniques

Our experimental evaluation systematically examines three core model optimization paradigms—quantization, pruning, and dynamic inference—across diverse neural architectures and datasets. The results demonstrate significant efficiency gains while highlighting nuanced trade-offs between computational performance and accuracy retention.

3.2.1. Quantization efficacy

As quantified in Table 2, INT8 precision delivers substantial inference acceleration across all models and batch sizes. For in-stance, ResNet50 achieves a 3.85× speedup at batch size 128, while MobileNet v1 attains a 6.21× improvement. This acceleration stems from reduced memory bandwidth requirements and streamlined integer operations, particularly beneficial for embedded hardware. Crucially, Table 3 reveals minimal accuracy degradation for most architectures: ResNet and VGG variants exhibit drops of <0.3%, and Inception v4 maintains near-identical accuracy. However, MobileNet v1 experiences a pronounced 1.55% decline, underscoring its sensitivity to precision reduction due to architectural constraints. Collectively, INT8 quantization balances high throughput with negligible accuracy loss for robust models but necessitates careful calibration for lightweight networks.

3.2.2. Pruning advantages

Structured pruning via QAT yields compelling efficiency gains, as evidenced in Table 4. VGG-19 reduces FLOPs by 56% with only a 0.04% accuracy drop, while ResNet-50 achieves 54% FLOPs reduction at a 0.52% accuracy cost. This efficiency arises from eliminating redundant filters without disrupting critical feature pathways. Notably, MobileNet v2 shows limited FLOPs reduction despite aggressive pruning, indicating diminishing returns in highly optimized architectures. Pruning’s primary strength lies in its hardware compatibility: structured sparsity aligns with parallel processing units, enabling deployment without specialized accelerators.

3.2.3. Dynamic inference flexibility

Table 5 highlights the adaptability of dynamic methods. DGNet excels for ResNet-50, reducing FLOPs by 57.2% while slightly improving accuracy. In contrast, FPGM and DynConv incur >1.3% accuracy penalties for similar FLOPs reductions. For MobileNet-v2, DGNet achieves 44% FLOPs savings with minimal degradation, outperforming MetaPruning. This variability underscores that dynamic inference’s efficacy hinges on sophisticated gating mechanisms—spatial-channel dual gating optimally skips redundant computations, whereas simpler policies struggle with accuracy preservation.

3.3. Cross-technique trade-offs and deployment implications

The interplay between optimization techniques reveals critical design considerations for embedded systems, synthesized in Table 6.

Quantization dominates in memory reduction and hardware acceleration potential but risks instability in lightweight models. Pruning offers moderate memory savings yet excels in FLOPs reduction with better generalization but demands iterative retraining.

For latency-critical edge devices, INT8 quantization is preferable; for energy-constrained systems where FLOPs directly correlate with power draw, pruning is superior.

Dynamic Inference as a hybrid solution, uniquely adapts computational cost per input, achieving 30–60% FLOPs reduction with near-zero accuracy loss. However, its runtime overhead and dependency on programmable logic limit deployment on fixed-function hardware. It is ideal for heterogeneous inputs but less suited for uniform data streams.

Consequently, no single optimization technique universally dominates, as each addresses distinct aspects of efficiency: quantization maximizes hardware utilization by leveraging low-precision arithmetic, pruning enhances computational efficiency through targeted sparsity, and dynamic inference optimizes re-source allocation by adapting to real-time demands. Therefore, for holistic embedded deployment, we recommend a context-dependent strategy: prioritizing quantization-first for platforms with dedicated hardware integer acceleration support to exploit its latency and energy benefits; employing structured pruning for GPU-accelerated platforms where its predictable sparsity patterns align well with parallel architectures; and adopting dynamic inference in scenarios characterized by significant workload variability to dynamically conserve resources during periods of lower demand, thereby optimizing the overall system efficiency.

4. Conclusion

This study comprehensively evaluates three pivotal model optimization paradigms—quantization, pruning, and dynamic inference—for deploying deep neural networks on resource-constrained embedded systems. Through rigorous experimentation across diverse architectures and datasets, we validate that each technique uniquely addresses the trilemma of computational efficiency, memory footprint, and accuracy retention. Quantization emerges as the foremost solution for memory compression and hardware acceleration. However, its vulnerability in lightweight architectures necessitates careful calibration, underscoring the critical role of model robustness in low-precision deployment.

Pruning, particularly structured variants via QAT, demonstrates exceptional efficacy in computational reduction. Its hard-ware compatibility with GPUs positions it as an ideal candidate for energy-constrained systems where FLOPs directly correlate with power consumption. Conversely, dynamic inference techniques like DGNet offer adaptive efficiency, dynamically reducing computation by 30–60% for variable-input scenarios while occasionally enhancing accuracy, albeit at the cost of runtime overhead and dependency on programmable logic.

Crucially, no single technique universally dominates; instead, their synergistic integration—such as quantized sparse models or hardware-aware dynamic policies—represents the most promising path toward ultra-efficient embedded AI. Future work must prioritize co-designing optimization techniques with lightweight model architectures to mitigate precision sensitivity. Cross-technique interoperability is under-explored. While quantization and pruning individually excel in memory and computation re-duction, their combined application often triggers cascading errors. Emerging frameworks must establish unified optimization methods.