1. Introduction

Inspired by the collective behavior of biological swarms, multi-agent systems (MAS), composed of multiple autonomous agents, have emerged as a pivotal technology for solving complex engineering problems [1]. Leveraging their inherent advantages in robustness, scalability, and task efficiency, multi-agent swarms demonstrate significant application potential in domains such as automated warehousing [2, 3], large-scale environmental monitoring [4, 5], and search and rescue [6, 7]. Consequently, the effective control of a swarm to accomplish complex formation shaping and collision avoidance tasks constitutes a central challenge in this field.

Currently, research in multi-agent formation control is primarily categorized into two major paradigms: target assignment-based methods and target-assignment-free self-organization. Target assignment-based methods [8, 9, 10] first assign explicit positions within the formation to each agent and then plan their respective paths. However, these approaches, particularly centralized strategies, suffer from high computational complexity and limited robustness, rendering them ill-suited for large-scale and dynamic scenarios [11, 12]. To address these limitations, target-assignment-free self-organization methods have emerged. Among these, a particularly promising direction, and the primary focus of this paper, is distributed formation control based on "shape discrete layers" [13]. This approach constructs a potential field that encodes the desired shape information, guiding agents to form up autonomously without explicit target assignments, thereby significantly enhancing the system's scalability and adaptability. However, similar to the traditional Artificial Potential Field (APF) method [14, 15], this approach is still susceptible to the risk of becoming trapped in local minima, failing to guarantee global path reachability in complex obstacle-laden environments.

To address this critical challenge, the shape discrete layer control framework was integrated with the A Star (A*) global pathfinding algorithm [16, 17], proposing a hybrid framework for distributed self-organizing formation control guided by a global path. The advantages of this hierarchical, decoupled strategy are significant. In a preprocessing step, the A* algorithm plans an optimal and safe global route. Subsequently, during the execution phase, the shape discrete layer controller guides the swarm to self-organize around this reference path while performing dynamic collision avoidance. The introduction of the A* algorithm fundamentally overcomes the propensity of purely self-organizing methods to become trapped in complex environments, thereby guaranteeing task reachability while fully preserving the advantages of distributed control in local dynamic obstacle avoidance and system robustness.

This paper is organized as follows: Section II provides a mathematical model and formal description of the multi-agent formation control problem. Section III elaborates on the proposed global path-guided distributed self-organizing formation control method, including the construction of the A* global path planner and the design of the shape discrete layer controller. In Section IV, a series of MATLAB simulation experiments are conducted to demonstrate and analyze the performance of the proposed method. Finally, Section V summarizes the work of the entire paper and points out potential directions for future research.

2. Problem statement

This paper studies the formation control problem for a swarm  $$ A=\{\mathrm{1,2},\dots ,N\}$$  consisting of  $$ N$$  identical mobile agents in a two-dimensional Euclidean space $$ W\subset {\mathbb{R}}^2$$ . For any agent  $$ i\in A$$ , its state at time t is described by its position  $$ p_i\left(t\right)\in {\mathbb{R}}^2$$  and velocity  $$ v_i\left(t\right)\in {\mathbb{R}}^2$$ . The kinematic model of the agents can be simplified to a first-order integrator:  $$ {\dot{p}}_i\left(t\right)=v_i\left(t\right)$$  Each agent is considered a circular entity with a radius of  $$ {\mathrm{r}}_{\mathrm{a}}$$ , and its speed is limited by a maximum value  $$ v_{\text{max}}$$ , i.e.,  $$ \Vert v_i\left(t\right)\Vert \le v_{\text{max}}$$ . The simulation environment W contains a set of M static obstacles  $$ O=\bigcup _{j=1}^M{O}_j$$ , where each obstacle  $$ O_j\subset W$$  is a bounded closed set. The task of the swarm is to migrate collectively from a specified starting region  $$ R_{\text{start}}\subset W$$  to a target region  $$ R_{\text{goal}}\subset W$$ . The core of this problem is to design a distributed control law  $$ u_i$$  for each agent i, such that under the control input  $$ v_i\left(t\right)=u_i$$ , the entire swarm can cooperatively achieve complex formation shaping, collective navigation, and collision avoidance.

3. Methods

3.1. Constructing the discrete layers of the formation shape

To determine the location of the formation, discrete layers of the formation shape are constructed within the formation environment. The agents can utilize the information from these discrete layers to determine the formation's position, and this information is also used in the subsequent calculation of the agents' velocities. In this paper, to better guide the agents into the black-colored area representing the formation shape, a grayscale iteration method is used to expand the influence of the central black area outwards. The iterative algorithm is designed as follows:

$$ {\delta }_q^k=\{\begin{array}{cc}\text{clip}\left({\mathrm{m}\mathrm{i}\mathrm{n}}_{q^{\text{'}}\in M_q}\right({\delta }_{q^{\text{'}}}^{k-1}+\frac{1}{K}),\mathrm{0,1}),& \text{if }{\delta }_q^1\ne 0\\ 0,& \text{if }{\delta }_q^1=0\end{array}$$(1)

In the formula,  $$ k=\mathrm{1,2},...,K-1$$  is a natural number.  $$ M_q\in Q$$ represents a  $$ 3\times 3$$  mask centered at $$ q$$ , and  $$ \text{clip}(\cdot )$$  indicates that the result is clamped to a given range.

After the operation of the equation above, the influence range of the formation shape is expanded. In a formation task, after the final formation shape is achieved, the ideal scenario is that  $$ n_{robot}$$  agents perfectly cover the formation shape; that is, the occupied area of the agents equals the area of the formation shape. Based on this relationship, the following equation exists:

$$ \frac{\pi }{4}{r}_{avoid}^2{n}_{robot}=\left|Q_T\right|l^2$$(2)

From which we derive:

$$ l=\frac{r_{avoid}}{2}\sqrt{\frac{\pi n_{robot}}{\left|Q_T\right|}}$$(3)

From the second equation, it can be seen that for a given collision avoidance radius  $$ r_{avoid}$$  and number of agents  $$ n_{robot}$$ , the side length l of each grid cell is inversely proportional to the number of grid cells  $$ \left|Q_T\right|$$  in the formation shape (the black area).

The actual simulation map area is generally larger than the area of the formation shape with its additional grid radius,  $$ \left|Q\right|$$ . Therefore, to construct discrete layers of the formation shape that are the same size as the actual map, cells with an area of  $$ l^2$$  and a weight of  $$ {\delta }_q=1$$  are used to fill the periphery of the formation shape  $$ Q$$ , expanding it to the size of the actual map. This completes the construction of the discrete layers of the formation shape, as shown in Figure 1.

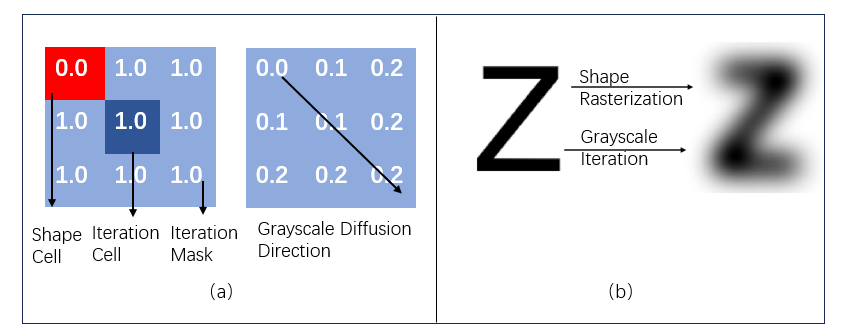
It is worth noting that in general formation design, it is often required that the number of target cells is the same as the number of agents participating in the formation, i.e.,  $$ n_{robot}=\left|Q_T\right|$$ , so that each agent can occupy one target cell in the final formation. When the number of agents is small, this condition can cause jagged edges on the outer contour of the formation shape, which is detrimental to the final formation effect. The controller constructed in this paper does not require this condition for formation and is applicable to situations where  $$ \left|Q_T\right|\ge n_{robot}$$ . It has been proven that the larger  $$ \left|Q_T\right|$$  is, the smaller the sawtooth effect on the outer contour of the shape, and the better the formation effect.

3.2. Dynamic negotiation

Within the framework for multi-agent formation control, a critical challenge is enabling the swarm to establish a common spatial reference, particularly in dynamic environments with obstacles. The system addresses this by employing a dynamic consensus protocol, a distributed method that allows all agents to collaboratively agree upon the geometric center of a target formation,  $$ P_c$$ , without receiving explicit location parameters from a central controller. This decentralized approach is vital for real-time adaptability, as it permits the entire formation to dynamically shift its assembly point to navigate around obstructions.

The foundation of this protocol is the mathematical representation of the inter-agent communication network as an undirected graph,  $$ G=(V,E)$$ , where  $$ V=\{V_1,V_2,\dots ,V_n\}$$  is the set of n agents, and E is the set of communication edges. The connectivity of this graph is formally described by the Adjacency Matrix,  $$ A\left(G\right)=\left[a_{ij}\right]$$ , whose elements are defined as follows:

$$ a_{ij}=\{\begin{array}{cc}1& \text{if }(v_j,v_i)\in E\\ 0& \text{if }(v_j,v_i)\notin E\end{array}$$(4)

The degree matrix of graph G is:

$$ D\left(G\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\sum _{j=1}^n{a}_{ij}\right)$$(5)

Therefore, the Laplacian matrix of graph G is:

$$ L\left(G\right)=\{\begin{array}{cc}\left[a_{ij}\right],& i\ne j\\ \left[\sum _{j=1,i\ne j}^n{a}_{ij}\right],& i=j\end{array}$$(6)

Expressed in matrix form as:

$$ L\left(G\right)=D\left(G\right)-A\left(G\right)$$(7)

Next, the discussion will proceed in a discrete-time framework. In the k-th negotiation step, the state of agent i, representing its estimate of the formation's center, is denoted by

$$ P_{C,i}\left(k\right)=\left(X_{c,i}\right(k),y_{c,i}(k\left)\right)$$(8)

A consensus on the formation's center is considered to be reached when the following condition is met for all agents:

$$ \underset{k\to k_{max}}{\mathrm{l}\mathrm{i}\mathrm{m}}\Vert P_{c,i}\left(k\right)-P_{c,j}\left(k\right)\Vert =0, \forall i,j\in V$$(9)

In this equation, k_maxrepresents the maximum number of negotiation iterations. The state of a single agent i at the next time step is given by:

$$ P_{c,i}(k+1)=P_{c,i}\left(k\right)+ϵu_i\left(k\right),ϵ<\frac{1}{d_{max}}$$(10)

where ε is the step size for each negotiation, and d_max is the maximum degree of the graph. The consensus protocol u_i(k) can be expressed as:

$$ u_i\left(k\right)=-\sum _{j\in N_i}{a}_{ij}\left(P_{c,i}\right(k)-P_{c,j}(k\left)\right),i\in V$$(11)

This can be written in matrix form for the entire system as:

$$ u\left(k\right)=-L\left(G\right)P_c\left(k\right)$$(12)

where

$$ P_c\left(k\right)={\left[P_{c,1}\right(k),P_{c,2}(k),\dots ,P_{c,n}(k\left)\right]}^T\text{ and }u\left(k\right)={\left[u_1\right(k),u_2(k),\dots ,u_n(k\left)\right]}^T$$

Thus, the position of the formation center at the next time step is given by:

$$ P_c(k+1)=(I-ϵL(G\left)\right)P_c\left(k\right)$$(13)

According to the consensus algorithm, through continuous interaction with neighboring agents, it is achieved that:  $$ \exists k_{\text{max}}>0\text{, such that for }k>k_{\text{max}},P_{c,i}\left(k\right)\to P_c$$ . The center of the discrete formation layer,  $$ q_m=(X_m,Y_m)$$ , is then aligned with the consensus position P_c in the simulation coordinate system, thereby achieving the positioning of the discrete formation layer on the simulation map.

3.3. Motion control law design

To achieve efficient, safe, and collision-free formation shaping in complex dynamic environments, the core of this research lies in designing a fully distributed motion control law for each agent. This strategy discards the complex centralized target assignment process found in traditional methods, endowing the system with greater robustness and scalability. The instantaneous velocity of each agent,  $$ v_i$$ , is synthesized through the vector addition of three functionally distinct and cooperative velocity components.

First, the formation entry control law,  $$ v_i^{ent}$$ , fulfills the function of global guidance. Its primary task is to guide agents from arbitrary initial positions to the target formation area, which is determined through collective dynamic negotiation. This control law is precisely defined by

$$ v_i^{ent}=c_1{\delta }_{q,i}\cdot \frac{P_{c,i}(k+m)-P_i\left(k\right)}{\Vert P_{c,i}(k+m)-P_i\left(k\right)\Vert }$$(14)

In this expression, the fractional part is a normalized unit vector that provides only the direction from the agent's current position,  $$ P_i\left(k\right)$$ , to its predicted future formation center,  $$ P_{c,i}(k+m)$$ , without affecting the magnitude of the velocity. The magnitude is primarily regulated by the gain coefficient  $$ c_1$$  and the key influence factor  $$ {\delta }_{q,i}$$ . This factor, representing the weight of the discrete cell the agent occupies, functions as a smooth switching mechanism. When an agent is far from the formation,  $$ {\delta }_{q,i}$$  is , allowing it to enter at a high speed. As it enters the formation's "grayscale" zone of influence,  $$ {\delta }_{q,i}$$  decreases, smoothly reducing the entry velocity. Finally, upon entering the target formation's core (black) area,  $$ {\delta }_{q,i}$$  becomes 0, completely deactivating this term. This effectively prevents overshoot and smoothly transfers control to the other components.

Second, to address the issue of edge congestion after agents enter the formation area and to achieve effective filling of the interior, we have designed the formation exploration control law,  $$ v_i^{exp}$$ . This component guides agents to actively explore unoccupied internal spaces. Its mechanism is twofold: first, when an agent occupies a region, it dynamically increases the weights of the relevant cells within its perception range using the formula

$$ {{\delta }^{\text{'}}}_{q_{op,i}}=\text{clip}({\delta }_{q_{op,i}}+\lambda (1-\frac{\left|\right|q_{op,i}-q_i\left|\right|}{r_{avoid}}),\mathrm{0,1})$$(15)

This is equivalent to leaving a "pheromone" in the environment, making the area less attractive to other agents. Subsequently, the agent calculates its exploration velocity according to the formula

$$ v_i^{exp}=c_2(1-{\delta }_{q,i})\frac{\sum _{q_{op,i}\in M_{op,i}}{{\delta }^{\text{'}}}_{q_{op,i}}(q_{op,i}-q_i)}{\left|\right|\sum _{q_{op,i}\in M_{op,i}}{{\delta }^{\text{'}}}_{q_{op,i}}(q_{op,i}-q_i)\left|\right|}$$(16)

The essence of which is to compute a resultant vector pointing towards surrounding "potential wells" (i.e., unoccupied darker regions). Notably, the factor  $$ (1-{\delta }_{q,i})$$  ensures that this exploration behavior is activated only after the agent has entered the formation's zone of influence, thus enabling an orderly transition of behaviors.

Finally, throughout the entire motion process, ensuring system safety and avoiding collisions is the highest priority task, which is handled by the collision avoidance control law,  $$ v_i^{avo}$$ . This law is designed to enable agents to evade both static environmental obstacles and dynamic neighboring agents. Its specific form is

$$ v_i^{avo}=c_3\frac{\sum _{\kappa =1}^s(P_i-P_{avo,i}^{\kappa })(r_{avoid}-||P_i-P_{avo,i}^{\kappa }|\left|\right)}{\left|\right|\sum _{\kappa =1}^s(P_i-P_{avo,i}^{\kappa })\left|\right|}$$(17)

which generates a repulsive vector at detected collision points,  $$ P_{avo,i}^{\kappa }$$ , creating an effective protective field. The magnitude of the repulsion is determined by the factor  $$ (r_{avoid}-||P_i-P_{avo,i}^{\kappa }|\left|\right)$$ , ensuring that the closer an agent is to an obstacle, the stronger the repulsive force it experiences, thereby achieving smooth and reliable avoidance.

In summary, the agent's final motion control law is obtained through the simple vector summation

$$ v_i=v_i^{ent}+v_i^{exp}+v_i^{avo}$$(18)

These three components function dynamically and cooperatively: at a distance,  $$ v_i^{ent}$$  dominates the motion; upon entering the formation area,  $$ v_i^{exp}$$  becomes dominant for fine-grained placement; and at any moment, if a collision risk is detected,  $$ v_i^{avo}$$  takes the highest priority. It is this superposition and synergy of simple yet effective distributed control laws that enables the entire multi-agent system to exhibit complex, intelligent, and emergent self-organizing formation behaviors.

3.4. Global path planning

When a multi-agent system executes formation tasks, in addition to relying on the aforementioned distributed motion control laws for local collision avoidance and formation keeping, a global path is also required to guide the entire formation from a starting point to a target area. To generate an optimal or near-optimal collision-free trajectory in an environment containing complex obstacles, this research adopts the A* algorithm as the foundation for global path planning. The environment for this algorithm is discretized into an  $$ N\times N$$  grid, where the state of each cell  $$ q=(x,y)$$  is recorded in an occupancy matrix,  $$ occ$$ . The core principle of the A* algorithm is to determine the next optimal node to explore by means of an evaluation function, expressed as:

$$ f\left(n\right)=g\left(n\right)+h\left(n\right)$$(19)

In this formula,  $$ g\left(n\right)$$  is the actual path cost from the start node S to the current node n, representing the cumulative sum of Euclidean distances between adjacent nodes along the path. It is specifically defined as

$$ g\left(n\right)={\sum }_{k=0}^{i-1}\left|\right|p_{k+1}-p_k\left|\right|$$(20)

where  $$ (p_0,p_1,...,p_i)$$  is the path from the start  $$ S=p_0$$  to the current node  $$ n=p_i$$ . The heuristic function  $$ h\left(n\right)$$  uses the straight-line Euclidean distance from the current node  $$ n$$  to the goal node  $$ G$$ , given by  $$ h\left(n\right)=\left|\right|n-G\left|\right|$$ . The algorithm maintains an open set of nodes to be explored, and in each iteration, it selects and expands the node  $$ n_{current}$$  with the minimum  $$ f\left(n\right)$$  value. For each neighbor  $$ n_{neighbor}$$ of  $$ n_{current}$$ , the algorithm calculates a tentative g-score:

$$ g_{tentative}=g\left(n_{current}\right)+\left|\right|n_{neighbor}-n_{current}\left|\right|$$(21)

Only if this tentative score is less than the previously recorded g-score for  $$ n_{neighbor}$$  will its parent node and cost be updated. When the algorithm expands to the goal node  $$ G$$ , it then reconstructs the optimal path by backtracking from the goal using a cameFrom map. To make this path more suitable for the motion of physical agents, it finally undergoes a line-of-sight based smoothing process to eliminate unnecessary waypoints.

4. Simulation

4.1. Simulation setup

To validate the effectiveness of the proposed global path-guided distributed self-organizing formation control framework, a series of simulation experiments were conducted using the MATLAB platform.

The experimental environment is set up as a 50m $$ \times $$ 50m two-dimensional space. To ensure environmental consistency between path planning and the multi-agent simulation, 10 point-obstacles with fixed coordinates are deployed in the scene. This obstacle layout is used for both global path planning and local agent obstacle avoidance.

Within this environment, the global path planning phase is executed first. The task for the A* algorithm is to compute an optimal global path from the start point (10, 10) to the goal point (40, 40), taking the aforementioned point-obstacles into account. This generated path does not contain complex dynamic information but serves as a macroscopic navigational reference, providing clear direction and guidance for the agent swarm in the subsequent phase.

In the multi-agent distributed control simulation phase, a swarm of 30 independent agents is initialized near the starting area of the global path. Their core task is to collaboratively track this pre-set global path while, at a local level, performing collision avoidance, maintaining safe distances, and dynamically adjusting relative positions through mutual communication and sensing. Ultimately, the swarm is required to successfully self-organize into a predefined 'snowflake' geometric configuration upon reaching the path's end region. This serves to demonstrate the effectiveness and robustness of the entire hierarchical control framework in guiding large-scale group movement, maintaining formation, and completing complex tasks.

4.2. A global path planning

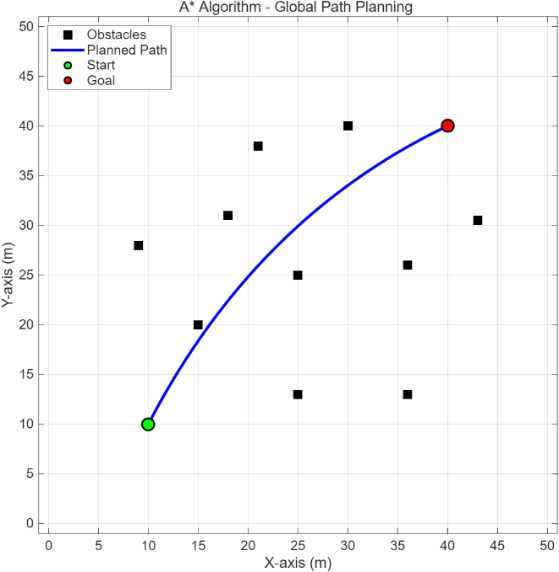
The first step of the framework is to generate a global reference path using the A* algorithm. The environment contains a set of pre-defined, static point-obstacles that the path must navigate around. As depicted in Figure 2, the A* algorithm's task is to compute an optimal path from the start point (green dot) at (10, 10) to the goal point (red dot) at (40, 40). During its search, the algorithm treats the grid cells occupied by the obstacles (black squares) as non-traversable. The resulting path, shown by the blue curve, is a smoothed trajectory that successfully weaves through the obstacle field. This path provides a globally optimal and safe reference trajectory for the subsequent multi-agent formation tracking task.

4.3. Multi-agent formation tracking and collision avoidance

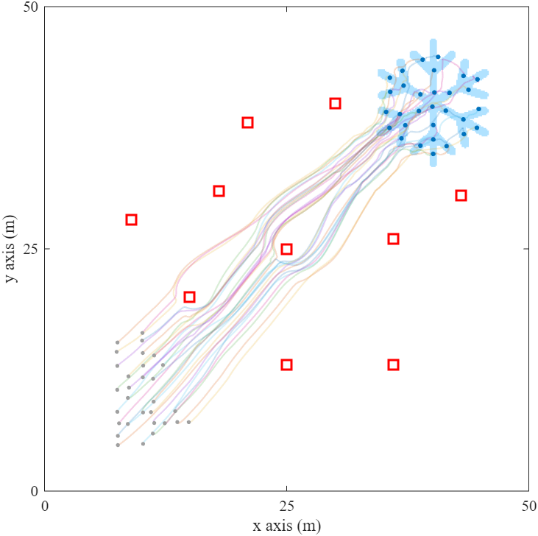
Once the global reference path was generated, the simulation proceeded to validate the self-organizing formation and path-tracking capabilities of the multi-agent swarm. Figure 3 illustrates the complete trajectories for this process. As depicted, the swarm, consisting of 30 agents, begins in the starting region and follows the A*-generated path as a macroscopic guide. The overall trajectory of the swarm aligns closely with this reference path. Throughout the process, each agent, distinguished by a unique trajectory color, leverages its distributed local controller. This allows each agent not only to maintain a safe distance from its neighbors to prevent internal collisions but also to preserve the overall cohesion of the swarm, enabling the collective to successfully navigate around all static obstacles (red squares). Ultimately, the swarm successfully converges into the desired "snowflake" formation upon arriving at the target region.

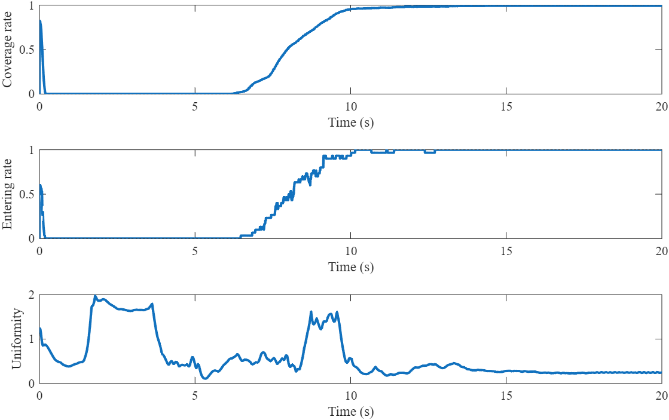
To quantitatively evaluate the performance of the proposed framework, Figure 4 presents the time-evolution of three key performance metrics: coverage rate, entering rate, and formation uniformity. As shown in the figure, both the entering rate and the coverage rate remain near zero for approximately the first 6 seconds, corresponding to the swarm's transit phase toward the target area. Subsequently, both metrics exhibit a rapid increase between t=6s and t=10s, reaching a stable value of 1, which indicates that all agents efficiently entered the target region and fully formed the 'snowflake' configuration within a 4-second window. Concurrently, the uniformity metric, which measures the spatial distribution of the agents (with lower values indicating higher uniformity), shows significant fluctuations during the initial transit and formation phases. However, after t=10s, as the formation stabilizes, the uniformity value sharply decreases and converges to a low, stable value, confirming the high quality and stability of the final configuration.

These simulation results clearly demonstrate the effectiveness of the proposed hybrid framework: the A* algorithm successfully addresses the challenges of global navigation and static obstacle avoidance in complex environments, while the distributed self-organizing controller ensures the swarm's local formation stability and dynamic collision avoidance capabilities during the execution of the global task.

5. Conclusion

This paper presents a hierarchical control framework for multi-agent systems that successfully integrates a "shape discrete layer" method for distributed self-organization with the A* algorithm for global path planning. This hybrid approach is designed to overcome a primary limitation of purely self-organizing methods: the risk of becoming trapped in local minima in complex, obstacle-laden environments. The primary contribution lies in the synergistic combination of these two techniques. The A* algorithm provides a guaranteed, globally reachable path, fundamentally solving the local minima issue, while the shape discrete layer controller preserves the key advantages of distributed systems, such as high scalability and robustness, by managing local formation shaping and dynamic collision avoidance.

The effectiveness of this framework was validated through a series of simulation experiments conducted in MATLAB. The results demonstrate that the swarm can accurately follow the globally planned path, effectively navigate complex static obstacle fields, and successfully self-organize into the predefined "snowflake" formation upon reaching the target destination. This confirms the successful synergy between the global planner and the local distributed controller.

While this research has achieved its primary objectives, several promising directions for future work remain. The current framework is validated in an environment with static obstacles; future efforts could focus on extending the model to handle dynamic or unknown environments, potentially by integrating a real-time replanning mechanism. Furthermore, expanding the control model from its current two-dimensional space to three-dimensional space would significantly broaden its applicability to more complex, real-world scenarios such as aerial swarm formations or underwater exploration. Finally, to bridge the gap between simulation and reality, a crucial next step will be to implement the proposed framework on a physical multi-robot platform, which would provide ultimate validation of the algorithm's effectiveness and robustness against real-world uncertainties like sensor noise, communication constraints, and actuation errors.