1. Introduction

Combinatorial counting is a fundamental branch of mathematics, with its core task being to answer the question, "How many possibilities are there?" However, when the objects being counted possess some form of symmetry, the problem becomes exceedingly complex. For instance, for a necklace with 6 beads to be colored with red and blue, how many "essentially different" patterns are there? Here, "essentially different" means that if one coloring pattern can be obtained from another by rotation or flipping, they are considered the same. Similarly, for a cube with its six faces colored with k colors, how many different coloring methods are there? These problems cannot be solved by simple permutation and combination formulas because their core lies in how to handle the equivalence relations caused by "symmetry."

Early explorations of such problems can be traced back to the mid-19th century. The chemist Arthur Cayley, while studying alkane isomers, encountered the problem of enumerating specific types of "tree" structures [1]. This can be seen as an early attempt at enumeration theory in a specific scientific problem, but its methods were rather specialized and lacked universality. The real theoretical breakthrough occurred at the end of the 19th century with Burnside’s Lemma (although its core idea was proposed earlier by Cauchy and Frobenius [2]). As the cornerstone of Pólya's theory—a primum mobile for modern enumeration—it furnished the first general equation for counting orbits (or equivalence classes) of a group action.

In 1937, the mathematician George Pólya set forth his opus insigne "Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen" [3], which systematically solved the problem of counting weighted equivalence classes. By introducing the core tool—the Cycle Index—Pólya not only unified but also greatly generalized previous methods, forming what we know today as the Pólya Enumeration Theorem (PET).

This study aims to:

1. Furnish rigorous demonstrations of Burnside’s Lemma and, subsequently, of Pólya’s Enumeration Theorem, with the latter encompassing both its unweighted and weighted forms.

2. Demonstrate the breadth and depth of its theoretical applications through examples in chemistry, graph theory, and music theory.

3. In-depthly explore the modern theoretical generalizations of Pólya’s theory, especially the work of de Bruijn, Rota, and Fujita, and analyze the connections and differences between these generalized theories and the classic PET.

4. Point out future research directions within a more abstract combinatorial framework, such as the Theory of Combinatorial Species.

2. Foundations in group theory

To rigorously discuss Pólya’s Enumeration Theorem, it’s necessary to first establish some fundamental concepts of group theory.

2.1. Basic definitions

Definition 2.1 (Group). A group is formally a pair  $$ \left(G,\mathrm{*}\right)$$  constituted by a non-empty set  $$ G$$  and a binary operation  $$ \mathrm{*}:G\times G\to G$$ . The fact that the codomain of  $$ \mathrm{*}$$  is  $$ G$$  itself establishes the closure property ex officio. For this pair to be deemed a group, three additional postulates must be satisfied [4]:

5. Associativity: The operation  $$ \mathrm{*}$$  is associative; scilicet, for any choice of  $$ a,b,c\in G$$ , equality  $$ \left(a\mathrm{*}b\right)\mathrm{*}c=a\mathrm{*}\left(b\mathrm{*}c\right)$$  holds.

6. Identity Element: There’s identity (or neutral) element  $$ e\in G$$ , a sine qua non for the structure, so that as to every  $$ a\in G$$ , we have  $$ e\mathrm{*}a=a\mathrm{*}e=a$$ .

7. Inverse Element: Each element  $$ a\in G$$  admits an inverse, denoted  $$ a^{-1}\in G$$ , for which  $$ a\mathrm{*}{a}^{-1}=a^{-1}\mathrm{*}a=e$$ .

Within the framework of Pólya’s theory, a group of cardinal importance is the symmetric group  $$ S_n$$ . This group comprises permutations sine exceptione (i.e., bijective functions) on finite set  $$ \left[n\right]$$  (first n integers’ set), among which function composition serves as group operation.

Definition 2.2 (Group Action). Let  $$ G$$  be a group and  $$ X$$  a non-empty set. A (left) group action means, de jure, a group homomorphism  $$ \Phi $$  from  $$ G$$  into the symmetric group on  $$ X$$ , denoted  $$ S_X$$[4]. Id est, an action means map  $$ \Phi :G\to S_X$$  satisfying  $$ \Phi \left(gh\right)=\Phi \left(g\right)\circ \Phi \left(h\right)$$  for any  $$ g,h\in G$$ .

The mapping  $$ \Phi $$  assigns to each group element  $$ g\in G$$  a specific permutation on  $$ X$$ , which we may denote  $$ {\varphi }_g:=\Phi \left(g\right)$$ . The action of  $$ g$$  on element  $$ x\in X$$  is subsequently defined as evaluation of this permutation:  $$ g\cdot x:={\varphi }_g\left(x\right)$$ .

The two customary axioms for a group action follow from this single definition ex necessitate legis:

8. Identity Action: A homomorphism maps identity element  $$ e\in G$$  to  $$ S_X$$  identity element, which is dentity permutation. Ergo,  $$ {\varphi }_e\left(x\right)=x$$ , or  $$ e\cdot x=x$$ .

9. Compatibility: The homomorphism property itself, viz.,  $$ \Phi \left(gh\right)=\Phi \left(g\right)\circ \Phi \left(h\right)$$ , directly implies compatibility:  $$ \left(gh\right)\cdot x={\varphi }_{gh}\left(x\right)=\left({\varphi }_g\circ {\varphi }_h\right)\left(x\right)={\varphi }_g\left({\varphi }_h\left(x\right)\right)=g\cdot \left(h\cdot x\right)$$ .

Prima facie, a group action elucidates the manner in which elements of  $$ G$$  systematically permute  $$ X$$  elements. Each group element  $$ g$$ , ergo, induces a permutation on  $$ X$$  in a fashion consonant with the group’s intrinsic structure.

Definition 2.3 (Orbit). Under group action  $$ G$$  on set  $$ X$$ , orbit of element  $$ x\in X$$  is set  $$ O_x=\{g\cdot x\mid g\in G\}$$[4,2]. It contains all the positions that  $$ x$$  can reach under the action of all elements in  $$ G$$ . All orbits shape a partition of set  $$ X$$ , meaning any two orbits are either identical or completely disjoint. An orbit is an equivalence class, and elements within the same orbit are considered "essentially the same." The core objective of Pólya’s theory is to count orbits’ amount.

Definition 2.4 (Stabilizer). The subset of  $$ G$$  comprising all elements whose action leaves a given point  $$ x\in X$$  invariant is denominated its stabilizer,  $$ G_x$$ :  $$ G_x=\{g\in G\mid g\cdot x=x\}$$[4,2]. This set is not merely a subset; it is, de jure, a subgroup of  $$ G$$ .

Definition 2.5 (Fixed Point). Regarding to any given  $$ g\in G$$ , the collection of points in  $$ X$$  rendered invariant by its action is termed  $$ g$$ ’s fixed-point set, and denoted  $$ X^g$$ :  $$ X^g=\{x\in X\mid g\cdot x=x\}$$[4,2].

Remark 2.6 (Difference between Stabilizer and Fixed Point). The distinction between these two constructs is fundamental, hinging on the universe of discourse. Ceteris paribus, the stabilizer  $$ G_x$$  is a subset of the group  $$ G$$ , populated by all transformations fixing a specific point  $$ x$$ . Mutatis mutandis, the fixed-point set  $$ X^g$$  denotes set  $$ X$$ ’s subset, populated by all points left invariant by a specific transformation  $$ g$$ .

2.2. Orbit-stabilizer theorem

Forthcoming theorem quantitatively elucidates nexus between the cardinality of an orbit and that of its stabilizer.

Theorem 2.7 (Orbit-Stabilizer Theorem). Let finite group  $$ G$$  act on set  $$ X$$ . As to any  $$ x\in X$$ , the cardinalities of its orbit  $$ O_x$$  and stabilizer  $$ G_x$$  are related to group order, pari passu, via following identity:

$$$ \left|G\right|=\left|O_x\right|\cdot \left|G_x\right|$$$

Proof. The proof rests upon the construction of a bijection, between set of left cosets of stabilizer,  $$ G/G_x=\{g{G}_x\mid g\in G\}$$ , and the orbit  $$ O_x$$ . Let us name this map  $$ \varphi $$ .

10. Define the map: We propose map  $$ \varphi :G/G_x\to O_x$$  given through rule  $$ \varphi \left(g{G}_x\right)=g\cdot x$$ . Its validity, i.e., its well-definedness, must be verified. Assume  $$ g_1{G}_x=g_2{G}_x$$ . This equality holds si et seulement si there’s several  $$ h\in G_x$$  so that  $$ g_1=g_{2}h$$ . The action on  $$ x$$  is then  $$ g_1\cdot x=\left(g_{2}h\right)\cdot x=g_2\cdot \left(h\cdot x\right)$$ . As  $$ h\in G_x$$ , its action on  $$ x$$  is trivial, ergo  $$ h\cdot x=x$$ . It obeys $$ \cdot x=g_2\cdot x$$ , confirming map is well-defined.

11. Injectivity: To establish injectivity, we must show that  $$ \varphi \left(g_1{G}_x\right)=\varphi \left(g_2{G}_x\right)$$  implies  $$ g_1{G}_x=g_2{G}_x$$ . Let’s assume the former:  $$ g_1\cdot x=g_2\cdot x$$ . Applying  $$ g_2^{-1}$$  action from the left yields  $$ g_2^{-1}\cdot \left(g_1\cdot x\right)=g_2^{-1}\cdot \left(g_2\cdot x\right)$$ . By compatibility, this simplifies to  $$ \left(g_2^{-1}{g}_1\right)\cdot x=e\cdot x=x$$ . This demonstrates, ipso facto, that the element  $$ g_2^{-1}{g}_1$$  belongs to stabilizer  $$ G_x$$ . Consequently,  $$ g_1{G}_x=g_2{G}_x$$ , proving  $$ \varphi $$  is injective.

12. Subjectivity: For subjectivity, consider an arbitrary element  $$ y\in O_x$$ . By the definition of an orbit, there must exist some  $$ g\in G$$  for which  $$ y=g\cdot x$$ . For this  $$ g$$ , a corresponding coset  $$ g{G}_x$$  exists a priori in the domain  $$ G/G_x$$ . Applying our map yields  $$ \varphi \left(g{G}_x\right)=g\cdot x=y$$ . Thus, every element in the codomain has a preimage, and  $$ \varphi $$  is surjective.

13. Conclusion: Having established that  $$ \varphi $$  denotes a bijection, it obeys that two sets are equinumerous:  $$ \left|G/G_x\right|=\left|O_x\right|$$ . Lagrange’s Theorem posits that subgroup index,  $$ \left|G:G_x\right|$$ , is given through  $$ \left|G\right|/\left|G_x\right|$$ . Equating the two expressions for the number of cosets gives  $$ \left|O_x\right|=\left|G\right|/\left|G_x\right|$$ . The theorem follows by rearrangement.

3. Core theorems and basic applications

3.1. Burnside’s Lemma

Burnside’s Lemma offers a method for enumerating orbits by relating their count to mean amount of fixed points and serves as fundamentum for Pólya’s theory of enumeration.

Theorem 3.1 (Burnside’s Lemma) [4]. Consider finite group  $$ G$$ 's action upon finite set  $$ X$$ . Orbits’s amount, denoted  $$ \left|X/G\right|$$ , is, in fine, arithmetic mean of cardinalities of fixed-point sets  $$ X^g$$  over all  $$ g\in G$$ :

$$$ \left|X/G\right|=\frac{1}{\left|G\right|}\sum _{g\in G}\left|X^g\right|$$$

Proof. proof’s modus operandi is to enumerate the elements of set  $$ S=\{\left(g,x\right)\in G\times X\mid g\cdot x=x\}$$  via two distinct methods. This set contains all pairs  $$ \left(g,x\right)$$  such that  $$ x$$  remains unchanged under the action of  $$ g$$ .

14. First Summation (grouping by group element  $$ g$$ ): Summing first over  $$ x\in X$$  per fixed  $$ g\in G$$ , the inner sum gives fixed-point set cardinality of  $$ g$$ , scilicet  $$ \left|X^g\right|$$ . A subsequent summation over all  $$ g\in G$$  yields the total cardinality.

$$$ \left|S\right|=\sum _{g\in G}\left|\{x\in X\mid g\cdot x=x\}\right|=\sum _{g\in G}\left|X^g\right|$$$

15. Second Summation (grouping by set element  $$ x$$ ): Alternatively, summing first over  $$ g\in G$$  per fixed  $$ x\in X$$ , inner sum is precisely stabilizer cardinality of  $$ x$$ ,  $$ \left|G_x\right|$$ . Summing then over all  $$ x\in X$$  yields the same total.

$$$ \left|S\right|=\sum _{x\in X}\left|\{g\in G\mid g\cdot x=x\}\right|=\sum _{x\in X}\left|G_x\right|$$$

16. Establishing the Equality: Equating the results of these two summation methods yields the pivotal equality:

$$$ \sum _{g\in G}\left|X^g\right|=\sum _{x\in X}\left|G_x\right|$$$

17. Introducing the Orbit-Stabilizer Theorem: According to Orbit-Stabilizer Theorem (Theorem 2.1), we have  $$ \left|G_x\right|=\frac{\left|G\right|}{\left|O_x\right|}$$ . Substituting this into the dextral side of the foregoing equality:

$$$ \sum _{g\in G}\left|X^g\right|=\sum _{x\in X}\frac{\left|G\right|}{\left|O_x\right|}$$$

18. Rearranging and Summing by Orbits: Transposing the constant  $$ \left|G\right|$$  to the sinistral side yields:

$$$ \frac{1}{\left|G\right|}\sum _{g\in G}\left|X^g\right|=\sum _{x\in X}\frac{1}{\left|O_x\right|}$$$

Now, consider the sum on the right. The set  $$ X$$  being partitioned by its orbits allows the sum over  $$ X$$  to be regrouped as a sum over orbits. Let  $$ X/G=\{O_1,O_2,...,O_k\}$$  be all orbits’ set, where  $$ k=\left|X/G\right|$$  is orbits’ total number.

$$$ \sum _{x\in X}\frac{1}{\left|O_x\right|}=\sum _{i=1}^k\sum _{x\in O_i}\frac{1}{\left|O_x\right|}$$$

For all elements  $$ x$$  in the same orbit  $$ O_i$$ , their orbit is  $$ O_i$$  itself, so the value of  $$ \left|O_x\right|$$  is constant and equal to  $$ \left|O_i\right|$$ . Thus, the inner sum has  $$ \left|O_i\right|$$  terms, each being  $$ \frac{1}{\left|O_i\right|}$$ .

$$$ \sum _{i=1}^k\sum _{x\in O_i}\frac{1}{\left|O_i\right|}=\sum _{i=1}^k\left(\left|O_i\right|\cdot \frac{1}{\left|O_i\right|}\right)=\sum _{i=1}^{k}1=k$$$

And  $$ k$$  means precisely orbits’ total number, i.e.,  $$ \left|X/G\right|$$ .

19. Conclusion: Collating the preceding chain of equalities yields the final result:

$$$ \left|X/G\right|=\frac{1}{\left|G\right|}\sum _{g\in G}\left|X^g\right|$$$

Example 3.2 (2-coloring vertices of a square [2]). Enumerate the distinct 2-colorings of vertices of a square with colors black and white, modulo rotational equivalence.

• Set  $$ X$$ : All possible coloring schemes. Each vertex has 2 choices, for 4 vertices, so  $$ \left|X\right|=2^4=16$$ .

• Group  $$ G$$ : The rotational group of the square  $$ C_4=\{e,r_{90},r_{180},r_{270}\}$$ , where  $$ e$$  is the identity (rotation by  $$ 0^{\circ }$$ ), and  $$ r_{90},r_{180},r_{270}$$  are clockwise rotations by  $$ {90}^{\circ },{180}^{\circ },{270}^{\circ }$$ . The order of the group is  $$ \left|G\right|=4$$ .

We now enumerate, seriatim, the cardinality of the fixed-point set for each group element  $$ g\in G$$ :

•  $$ g=e$$  (rotation by  $$ 0^{\circ }$$ ): All 16 colorings remain unchanged.  $$ \left|X^e\right|=16$$ .

•  $$ g=r_{90}$$  (rotation by  $$ {90}^{\circ }$$ ): The vertices are permuted as  $$ \left(1\to 2\to 3\to 4\to 1\right)$$ . As to coloring to keep the same level after a  $$ {90}^{\circ }$$  rotation, all four vertices must have the same color. There are 2 such schemes (all white or all black).  $$ \left|X^{r_{90}}\right|=2$$ .

•  $$ g=r_{180}$$  (rotation by  $$ {180}^{\circ }$$ ): The induced permutation on the vertices is  $$ \left(1 3\right)\left(2 4\right)$$ . A coloring remains invariant under this action if, and only if, the vertices within each cycle are monochromatic. This de facto reduces the problem to choosing one color for the pair  $$ \{1,3\}$$  and one for the pair  $$ \{2,4\}$$ . With two available colors, this gives  $$ 2\times 2=4$$  invariant configurations. Ergo,  $$ \left|X^{r_{180}}\right|=4$$ .

•  $$ g=r_{270}$$  (rotation by  $$ {270}^{\circ }$$ ): The vertices are permuted as  $$ \left(1\to 4\to 3\to 2\to 1\right)$$ . Symmetrical to the  $$ r_{90}$$  case, all four vertices must be the same color.  $$ \left|X^{r_{270}}\right|=2$$ .

According to Burnside’s Lemma, different coloring schemes’ number is:

$$$ \left|X/G\right|=\frac{1}{4}\left(\left|X^e\right|+\left|X^{r_{90}}\right|+\left|X^{r_{180}}\right|+\left|X^{r_{270}}\right|\right)=\frac{1}{4}\left(16+2+4+2\right)=\frac{24}{4}=6$$$

So there are 6 essentially different coloring schemes.

3.2. Pólya Enumeration Theorem (PET)

Burnside’s Lemma can only answer "how many" equivalence classes there are, while Pólya’s Enumeration Theorem can further answer "how many of each type" of equivalence class exist.

3.2.1. Preliminary concepts

• Function Set  $$ Y^X$$ : Let  $$ X$$  be a finite object set and  $$ Y$$  a color set. A specific coloring of  $$ X$$  is, de jure, a function  $$ f:X\to Y$$ . All such functions’ set is denoted  $$ Y^X$$ .

• Induced Group Action: Group  $$ G$$ 's action upon  $$ X$$  gives rise to a corresponding action on the function set  $$ Y^X$$ . For any  $$ g\in G$$  and  $$ f\in Y^X$$ , the resultant function  $$ g\cdot f$$  is defined via  $$ \left(g\cdot f\right)\left(x\right)=f\left(g^{-1}\cdot x\right)$$ . (This definition constitutes a valid group action as it satisfies identity axiom,  $$ e\cdot f=f$$ , and the compatibility axiom,  $$ \left(gh\right)\cdot f=g\cdot \left(h\cdot f\right)$$ . The use of  $$ g^{-1}$$  is a standard convention to ensure it is a left action.)

• Configuration: Under the induced group action, an orbit in  $$ Y^X$$  is called a configuration, representing a set of essentially identical coloring schemes.

• Type of a Permutation: Type of permutation  $$ p$$  is a vector  $$ \left(b_1,b_2,...,b_n\right)$$ , with each component  $$ b_i$$  enumerating cycles’ number of length  $$ i$$  within permutation’s disjoint cycle factorization.

• Cycle Index: Cycle index of group  $$ G$$  acting upon set  $$ X$$  of cardinality  $$ n$$  means polynomial in the variables  $$ x_1,x_2,...,x_n$$ , given via formula:

$$$ Z_G\left(x_1,...,x_n\right)=\frac{1}{\left|G\right|}\sum _{g\in G}\prod _{i=1}^n{x}_i^{b_i\left(g\right)}$$$

• In which,  $$ b_i\left(g\right)$$  denotes cyless’ number of length  $$ i$$  in the permutation corresponding to the group element  $$ g$$ . This polynomial serves as an algebraic summary of the group’s action, encoding, in toto, the cycle structure of every element.

3.2.2. PET unweighted form

Theorem 3.3 (PET, Unweighted Form). A set  $$ X$$  is acted by finite group  $$ G$$ , with a palette of  $$ k$$  colors available for use. The number of inequivalent colorings (i.e., configurations) is, verbatim, the evaluation of the cycle index polynomial  $$ Z_G$$  at  $$ x_i=k$$  for all  $$ i=1,\dots ,n$$ :

$$$ \left|Y^X/G\right|=Z_G\left(k,k,...,k\right)$$$

Proof.

20. Burnside’s Lemma posits that  $$ \left|Y^X/G\right|=\frac{1}{\left|G\right|}\sum _{g\in G}\left|{\left(Y^X\right)}^g\right|$$ . Herein,  $$ {\left(Y^X\right)}^g$$  represents the set of functions (or colorings) rendered invariant by the action of  $$ g$$ .

21. Our immediate objective is the enumeration of  $$ \left|{\left(Y^X\right)}^g\right|$$ . A coloring  $$ f\in Y^X$$  qualifies as a fixed point of  $$ g$$  si et seulement si  $$ g\cdot f=f$$ .

22. Definition of induced action necessitates that for any  $$ x\in X$$ , the equality  $$ f\left(g^{-1}\cdot x\right)=f\left(x\right)$$  must hold. Let  $$ x\mathrm{\text{'}}=g^{-1}\cdot x$$ , which implies  $$ x=g\cdot x\mathrm{\text{'}}$$ . The condition becomes,  $$ f\left(x\mathrm{\text{'}}\right)=f\left(g\cdot x\mathrm{\text{'}}\right)$$ , for all  $$ x\mathrm{\text{'}}\in X$$ .

23. This condition implies that for any cycle in the permutation induced by  $$ g$$  on  $$ X$$ , all elements within that cycle must have the same color value under the coloring scheme  $$ f$$ . In other words,  $$ f$$  must be a constant function on each cycle of  $$ g$$ .

24. Let the cycle decomposition of the permutation corresponding to  $$ g$$  have  $$ c\left(g\right)=\sum _{i=1}^n{b}_i\left(g\right)$$  cycles. For each cycle, we can independently choose one color from  $$ Y$$ . Since  $$ \left|Y\right|=k$$ , there’re  $$ k$$  color choices per cycle.

25. Therefore, fixed-point colorings’ total amount is  $$ \left|{\left(Y^X\right)}^g\right|=k^{c\left(g\right)}=k^{\sum _i{b}_i\left(g\right)}=\prod _{i=1}^n{k}^{b_i\left(g\right)}$$ .

26. Substituting this result into the formula of Burnside’s Lemma:

$$$ \left|Y^X/G\right|=\frac{1}{\left|G\right|}\sum _{g\in G}{k}^{c\left(g\right)}=\frac{1}{\left|G\right|}\sum _{g\in G}\prod _{i=1}^n{k}^{b_i\left(g\right)}$$$

27. This is precisely the result obtained by substituting  $$ x_i=k$$  into the definition of the cycle index  $$ Z_G\left(x_1,...,x_n\right)$$ . Therefore,

$$$ \left|Y^X/G\right|=Z_G\left(k,k,...,k\right)$$$

3.2.3. PET weighted form

Preliminary Concepts:

• Weight: Assign a unique symbol (formal variable) to each color. For example, the weight of Red (R) is  $$ r$$ , and Blue (B) is  $$ b$$ .

• Weight of a Coloring: Coloring scheme weight is product of weights of colors upon all its objects. For example, a four-bead necklace colored (R, B, R, B) has a weight of  $$ W\left(f\right)=w\left(R\right)\cdot w\left(B\right)\cdot w\left(R\right)\cdot w\left(B\right)=r^2{b}^2$$ . This weight precisely records that the scheme has "2 red beads and 2 blue beads."

• Pattern Inventory or Configuration Generating Function (CGF): The sum of weights of all non-equivalent colorings (namely, all configurations). For example,  $$ F\left(r,b\right)=r^4+r^{3}b+2r^2{b}^2+...$$  means: there is 1 all-red pattern, 1 pattern with 3 reds and 1 blue, 2 patterns with 2 reds and 2 blues, etc.

Theorem 3.4 (PET, Weighted Form). Let the weight of color  $$ y_j\in Y$$  be  $$ w\left(y_j\right)$$ . The configuration generating function  $$ F$$  is gained via insteading specific power sums into cycle index:

$$$ F=Z_G\left(\sum _{j}w\left(y_j\right),\sum _{j}w{\left(y_j\right)}^2,...,\sum _{j}w{\left(y_j\right)}^n\right)$$$

That is, replace the variable  $$ x_k$$  with the sum of the  $$ k$$ -th powers of all color weights,  $$ \sum _{j}w{\left(y_j\right)}^k$$ .

Proof.

28. The proof’s fulcrum means Burnside’s Lemma weighted version, which posits an equality between the sum of all orbit weights and the mean of all fixed-point-set weights. The generating function for configurations, ergo, is:

$$$ F=\sum _{C\in \mathcal{C}}W\left(C\right)=\frac{1}{\left|G\right|}\sum _{g\in G}\left(\sum _{f\in {\left(Y^X\right)}^g}W\left(f\right)\right)$$$

Herein,  $$ W\left(C\right)$$  is the weight common to all colorings in an orbit  $$ C$$ , and  $$ {\left(Y^X\right)}^g$$  is the set of colorings rendered invariant by the action of  $$ g$$ .

29. The immediate objective is to evaluate the inner summation, viz., the total weight of the fixed-point set  $$ {\left(Y^X\right)}^g$$  for a given  $$ g$$ .

30. A sine qua non for a coloring  $$ f$$  to be a fixed point of  $$ g$$  is that  $$ f$$  must be constant on each cycle of the permutation induced by  $$ g$$ . Let the cycle decomposition of  $$ g$$  be  $$ C_1,C_2,...,C_{c\left(g\right)}$$ .

31. The weight of such an invariant coloring  $$ f$$  factorizes over the cycles of  $$ g$$ . For a cycle  $$ C_j$$  on which  $$ f$$  is constant with color  $$ y_s\in Y$$ , its contribution to the product is ipso facto  $$ {\left(w\left(y_s\right)\right)}^{\left|C_j\right|}$$ .

$$$ W\left(f\right)=\prod _{x\in X}w\left(f\left(x\right)\right)=\prod _{j=1}^{c\left(g\right)}{\left(w\left(y_{s_j}\right)\right)}^{\left|C_j\right|}$$$

32. Summing  $$ W\left(f\right)$$  over all  $$ f\in {\left(Y^X\right)}^g$$ , the independence of color choices for each cycle permits the interchange of summation and product:

$$$ \sum _{f\in {\left(Y^X\right)}^g}W\left(f\right)=\prod _{j=1}^{c\left(g\right)}\left(\sum _{s=1}^{\left|Y\right|}{\left(w\left(y_s\right)\right)}^{\left|C_j\right|}\right)$$$

33. Regrouping the product by cycle length  $$ i$$ , the contribution from the  $$ b_i\left(g\right)$$  cycles of length  $$ i$$  is jointly  $$ {\left(\sum _{j=1}^{\left|Y\right|}w{\left(y_j\right)}^i\right)}^{b_i\left(g\right)}$$ . The total sum is the product over all  $$ i$$ :

$$$ \sum _{f\in {\left(Y^X\right)}^g}W\left(f\right)=\prod _{i=1}^n{\left(\sum _{j=1}^{\left|Y\right|}w{\left(y_j\right)}^i\right)}^{b_i\left(g\right)}$$$

34. Substituting this result into the weighted Burnside’s Lemma, we get:

$$$ F=\frac{1}{\left|G\right|}\sum _{g\in G}\prod _{i=1}^n{\left(\sum _{j=1}^{\left|Y\right|}w{\left(y_j\right)}^i\right)}^{b_i\left(g\right)}$$$

• This is precisely the result of replacing each variable  $$ x_i$$  in the cycle index  $$ Z_G\left(x_1,...,x_n\right)$$  with  $$ \sum _{j=1}^{\left|Y\right|}w{\left(y_j\right)}^i$$ .

3.2.4. Application examples

Example 3.5 (Chemistry: Isomers of Dichlorobenzene ( $$ C_6{H}_{4}C{l}_2$$ ) [2]). This problem can be viewed as coloring the 6 vertices of a benzene ring with 4 hydrogen atoms (H) and 2 chlorine atoms (Cl). The symmetry group is the dihedral group  $$ D_6$$ .

• Objects  $$ X$$ : The 6 hydrogen positions on the benzene ring,  $$ \left|X\right|=6$$ .

• Colors  $$ Y$$ : {H, Cl}.

• Group  $$ G$$ :  $$ D_6$$ , acting on the 6 vertices, with order 12. It contains 6 rotations (including identity) and 6 reflections.

The cycle index of  $$ D_6$$  acting on 6 vertices is:

$$$ Z_{D_6}\left(x_1,\dots ,x_6\right)=\frac{1}{12}\left(x_1^6+2x_6^1+2x_3^2+4x_2^3+3x_1^2{x}_2^2\right)$$$

Let the weight of H be  $$ h$$  and Cl be  $$ c$$ . According to the weighted PET, we replace  $$ x_k$$  with  $$ h^k+c^k$$ :

$$$ \begin{array}{cc}F\left(h,c\right)=Z_{D_6}\left(h+c,h^2+c^2,\dots ,h^6+c^6\right)=\frac{1}{12}[& {\left(h+c\right)}^6+2\left(h^6+c^6\right)+2{\left(h^3+c^3\right)}^2\\ & +4{\left(h^2+c^2\right)}^3+3{\left(h+c\right)}^2{\left(h^2+c^2\right)}^2]\end{array}$$$

We are interested in the coefficient of the  $$ h^4{c}^2$$  term. We expand each term and extract this coefficient:

• $$ {\left(h+c\right)}^6⟹\left(\genfrac{}{}{0pt}{}{6}{2}\right)h^4{c}^2=15h^4{c}^2$$

• $$ 2\left(h^6+c^6\right)⟹0$$

• $$ 2{\left(h^3+c^3\right)}^2=2\left(h^6+2h^3{c}^3+c^6\right)⟹0$$

• $$ 4{\left(h^2+c^2\right)}^3=4\left(h^6+3h^4{c}^2+3h^2{c}^4+c^6\right)⟹4\cdot 3h^4{c}^2=12h^4{c}^2$$

• $$ 3{\left(h+c\right)}^2{\left(h^2+c^2\right)}^2=3\left(h^2+2hc+c^2\right)\left(h^4+2h^2{c}^2+c^4\right)$$  The  $$ h^4{c}^2$$  term comes from  $$ h^2\cdot 2h^2{c}^2$$  and  $$ c^2\cdot h^4$$ .  $$ 3\left(h^2\left(2h^2{c}^2\right)+c^2\left(h^4\right)\right)=3\left(2h^4{c}^2+h^4{c}^2\right)=3\left(3h^4{c}^2\right)=9h^4{c}^2$$ .

So the total coefficient is  $$ 15+12+9=36$$ . The final coefficient is  $$ \frac{36}{12}=3$$ . A coefficient of 3 for the term  $$ h^4{c}^2$$  signifies the existence of three distinct dichlorobenzene isomers, known nominatim as the ortho, meta, and para configurations.

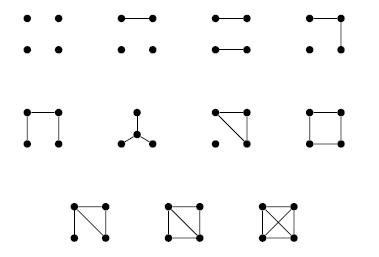
Example 3.6 (Graph Theory: Non-isomorphic graphs on 4 vertices [4]). This problem can be viewed as 2-coloring (edge "exists" or "does not exist") the 6 edges of a complete graph  $$ K_4$$ .

• Objects  $$ X$$ : The 6 edges of  $$ K_4$$ .

• Colors  $$ Y$$ : {exists, does not exist}, so the number of colors is  $$ k=2$$ .

• Group  $$ G$$ : The symmetric group  $$ S_4$$  acting on the 4 vertices induces a permutation group on the 6 edges, let’s call it  $$ G$$ .  $$ \left|G\right|=\left|S_4\right|=24$$ .

This induced group  $$ G$$ ’s cycle index should be calaculated. This asks for analyzing how each type of permutation in  $$ S_4$$  acts on the set of edges.

• Identity (1 element):  $$ \left(1\right)\left(2\right)\left(3\right)\left(4\right)$$ . All edges are fixed. Permutation type is  $$ x_1^6$$ .

• Transpositions (6 elements): e.g.,  $$ \left(12\right)\left(3\right)\left(4\right)$$ . Edge  $$ \left(34\right)$$  is fixed. Edge pairs  $$ \left(\left(13\right),\left(23\right)\right)$$  and  $$ \left(\left(14\right),\left(24\right)\right)$$  are swapped. Edge  $$ \left(12\right)$$  is fixed. Permutation type is  $$ x_1^2{x}_2^2$$ .

• 3-cycles (8 elements): e.g.,  $$ \left(123\right)\left(4\right)$$ . Edge pairs  $$ \left(\left(14\right),\left(24\right),\left(34\right)\right)$$  and  $$ \left(\left(12\right),\left(23\right),\left(13\right)\right)$$  form two 3-cycles. Permutation type is  $$ x_3^2$$ .

• 4-cycles (6 elements): e.g.,  $$ \left(1234\right)$$ . Edge pair  $$ \left(\left(12\right),\left(23\right),\left(34\right),\left(14\right)\right)$$  forms a 4-cycle. Edges  $$ \left(13\right)$$  and  $$ \left(24\right)$$  are swapped. Permutation type is  $$ x_2{x}_4$$ .

• Double transpositions (3 elements): e.g.,  $$ \left(12\right)\left(34\right)$$ . Edges  $$ \left(12\right)$$  and  $$ \left(34\right)$$  are fixed. Edge pairs  $$ \left(\left(13\right),\left(24\right)\right)$$  and  $$ \left(\left(14\right),\left(23\right)\right)$$  are swapped. Permutation type is  $$ x_1^2{x}_2^2$$ .

Thus, the cycle index is:

$$$ Z_G=\frac{1}{24}\left(x_1^6+6x_1^2{x}_2^2+8x_3^2+6x_2{x}_4+3x_1^2{x}_2^2\right)=\frac{1}{24}\left(x_1^6+9x_1^2{x}_2^2+8x_3^2+6x_2{x}_4\right)$$$

Applying the unweighted PET, with number of colors  $$ k=2$$ :

$$$ \begin{array}{cc}\text{Number}\text{of}\text{graphs}& =Z_G\left(2,2,2,2\right)\\ & =\frac{1}{24}\left(2^6+9\cdot 2^2\cdot 2^2+8\cdot 2^2+6\cdot 2\cdot 2\right)\\ & =\frac{1}{24}\left(64+144+32+24\right)\\ & =\frac{264}{24}=11\end{array}$$$

It follows, ergo, that the enumeration of simple graphs on 4 vertices, modulo isomorphism, yields a total of 11.

Example 3.7 (Music Theory: Counting Triads [2]). The number of essentially different triads in twelve-tone equal temperament.

• Objects  $$ X$$ : All 3-element subsets of the 12 pitches  $$ \{0,1,...,11\}$$ , for a total of  $$ \left(\genfrac{}{}{0pt}{}{12}{3}\right)=220$$ .

• Group  $$ G$$ : The transposition group  $$ {\mathbb{Z}}_{12}$$ , acting as  $$ k\cdot \{a,b,c\}=\{a+k,b+k,c+k\} \left(\mathrm{m}\mathrm{o}\mathrm{d} 12\right)$$ .

Calculating fixed-point set size via Burnside’s Lemma:

•  $$ k=0$$  (identity): All 220 triads are unchanged.  $$ \left|X^0\right|=220$$ .

• A triad  $$ \{a,b,c\}$$  is invariant under transposition by  $$ k$$  if the set  $$ \{a+k,b+k,c+k\}$$  (mod 12) is the same as  $$ \{a,b,c\}$$ . This requires transposition by  $$ k$$  to be a symmetry operation of the chord.

•  $$ k=1,2,3,5,6,7,9,10,11$$ : For these transposition amounts, a set can only be invariant if all pitches are the same, which contradicts the definition of a triad as a "3-element subset". So  $$ \left|X^k\right|=0$$ .

•  $$ k=4$$  (transposition by 4 semitones): The fixed points are chords constructed from notes 4 semitones apart, i.e., augmented triads. For example,  $$ \{0,4,8\}$$ . After transposition by 4, it becomes  $$ \{4,8,0\}$$ , which is the same set. There are 4 such chords:  $$ \{0,4,8\},\{1,5,9\},\{2,6,10\},\{3,7,11\}$$ . So  $$ \left|X^4\right|=4$$ .

•  $$ k=8$$  (transposition by 8 semitones): Same as the  $$ k=4$$  case, the fixed points are the same 4 augmented triads. So  $$ \left|X^8\right|=4$$ .

Number of orbits =  $$ \frac{1}{12}\left(220+0\cdot 8+4+4\right)=\frac{1}{12}\left(220+4+4\right)=\frac{228}{12}=19$$ .

4. Generalizations of Pólya’s enumeration theorem

While the classic PET is powerful, its application scenarios are still limited. Later mathematicians generalized it from different perspectives, greatly expanding its theoretical content and range of applications.

4.1. de Bruijn’s theorem: dual group action

The classic Pólya theory only considers one group  $$ G$$  acting on the object set  $$ X$$ . De Bruijn generalized this to the case where another group  $$ H$$  simultaneously acts on the color set  $$ Y$$[4]. For example, when coloring the vertices of a square, we might not only consider rotations as equivalent but also permutations of colors (e.g., red becomes blue, blue becomes red) as equivalent.

Definition 4.1 (Generalized Function Equivalence). Let  $$ f_1$$  and  $$ f_2$$  be two colorings in  $$ Y^X$$ . They are defined as equivalent inter se as there's pair  $$ \left(g,h\right)\in G\times H$$  so that equality below holds for any choice of  $$ x\in X$$ :

$$$ f_2\left(x\right)=h\left(f_1\left(g^{-1}x\right)\right)$$$

This definition establishes an equivalence relation on  $$ Y^X$$  that is, ipso facto, action result from direct product group  $$ G\times H$$ .

Theorem 4.2 (de Bruijn’s Theorem). Consider group action of  $$ G$$  upon set  $$ X$$  and, pari passu, action of group  $$ H$$  upon color set  $$ Y$$ . Total enumeration of inequivalent colorings, sub specie the generalized equivalence, is furnished by the formula:

$$$ \left|\left(Y^X\right)/\left(G\times H\right)\right|=\frac{1}{\left|G\right|\left|H\right|}\sum _{g\in G}\sum _{h\in H}\prod _{i=1}^n{\left(\sum _{j|i}j\cdot c_j\left(h\right)\right)}^{b_i\left(g\right)}$$$

Herein,  $$ b_i\left(g\right)$$  enumerates length i’s cycles in permutation upon  $$ X$$  induced from  $$ g$$ ; mutatis mutandis,  $$ c_j\left(h\right)$$  enumerates length j’s cycles in permutation upon  $$ Y$$  induced from  $$ h$$ . Inner summation extends over all positive integers  $$ j$$  that are divisors of  $$ i$$ .

Proof. The argument proceeds by applying Burnside’s Lemma ad hoc to direct product group  $$ G\times H$$  action upon function set (colorings)  $$ Y^X$$ .

35. Application of Burnside’s Lemma: Per Burnside’s Lemma, count of orbits (inequivalent colorings) equates to mean number of fixed points. Product group order is, ex hypothesi,  $$ \left|G\times H\right|=\left|G\right|\left|H\right|$$ . The lemma, thus, takes the form:

$$$ \left|\left(Y^X\right)/\left(G\times H\right)\right|=\frac{1}{\left|G\right|\left|H\right|}\sum _{\left(g,h\right)\in G\times H}\left|{\left(Y^X\right)}^{\left(g,h\right)}\right|$$$

• The term  $$ {\left(Y^X\right)}^{\left(g,h\right)}$$  herein denotes the set of functions  $$ f\in Y^X$$  rendered invariant by action of pair  $$ \left(g,h\right)$$ .

36. Analyze the Fixed-Point Condition: Function  $$ f$$  means fixed point of  $$ \left(g,h\right)$$  as and only as  $$ \left(g,h\right)\cdot f=f$$ . By definition, this means:

$$$ f\left(x\right)=h\left(f\left(g^{-1}x\right)\right) \text{for}\text{all}x\in X$$$

• Let  $$ x\mathrm{\text{'}}=g^{-1}x$$ , which implies  $$ x=gx\mathrm{\text{'}}$$ . Substituting this into the condition, we get a condition that must hold for all  $$ x\mathrm{\text{'}}\in X$$ :

$$$ f\left(gx\mathrm{\text{'}}\right)=h\left(f\left(x\mathrm{\text{'}}\right)\right)$$$

37. Decomposition by Cycles of  $$ g$$ : This condition implies that the coloring  $$ f$$  must be consistent across the cycles of the permutation  $$ g$$ . Let’s consider a single cycle  $$ C=\left(x_1,x_2,\dots ,x_i\right)$$  of length  $$ i$$  in X permutation induced from  $$ g$$ . The elements are related by  $$ x_2=g{x}_1,x_3=g{x}_2,\dots ,x_1=g{x}_i$$ .

• Let the elements  $$ \left(x_1,x_2,\dots ,x_i\right)$$  constitute a cycle of length  $$ i$$  induced by the permutation  $$ g$$ . An iterative application of the condition  $$ f\left(g\cdot x\right)=h\left(f\left(x\right)\right)$$  along this cycle yields a general formula for any element  $$ x_k$$  therein:

$$$ f\left(x_k\right)=h^{k-1}\left(f\left(x_1\right)\right) \text{for}\text{the}\text{index}k\in \{1,\dots ,i\}$$$

• where  $$ h^0$$  is taken to be the identity map. The closure of the cycle, i.e.,  $$ x_1=g\cdot x_i$$ , imposes, ipso facto, the crucial constraint:

$$$ f\left(x_1\right)=h^i\left(f\left(x_1\right)\right)$$$

• This tells us two crucial things:

• The entire sequence of colors  $$ \{f\left(x_1\right),f\left(x_2\right),\dots ,f\left(x_i\right)\}$$  is determined via choice of first color  $$ y_1=f\left(x_1\right)$$ . Colors’ sequence must lie within an orbit of the action of  $$ H$$  on  $$ Y$$ .

• The choice of  $$ y_1=f\left(x_1\right)$$  is not arbitrary. It must satisfy the condition  $$ y_1=h^i\left(y_1\right)$$ . This means that  $$ y_1$$  must belong to a cycle of the permutation  $$ h$$  whose length, let’s say  $$ j$$ , divides the length  $$ i$$  of the cycle  $$ C$$ .

38. Count the Choices for a Single Cycle: Consider a cycle  $$ C$$  of length  $$ i$$  induced by  $$ g$$ . The constraint  $$ h^i\left(f\left(x_1\right)\right)=f\left(x_1\right)$$ , established supra, necessitates that the color choice for  $$ f\left(x_1\right)$$  must be an element  $$ y\in Y$$  whose orbit under the action of  $$ h$$  has a length, say  $$ j$$ , that divides  $$ i$$ . Action of  $$ h$$  partitions color set  $$ Y$$  into disjoint cycles; let  $$ c_j\left(h\right)$$  stand for count of cycles of length  $$ j$$ . Colors’ number residing in such cycles of length  $$ j$$  is  $$ j\cdot c_j\left(h\right)$$ . The complete enumeration of valid choices for  $$ f\left(x_1\right)$$  is, ergo, the sum of these quantities over all compatible cycle lengths  $$ j$$ :

$$$ \text{Number}\text{of}\text{choices}\text{for}\text{cycle}C=\sum _{j|i}j\cdot c_j\left(h\right)$$$

39. Combine for All Cycles: The choices of coloring for different cycles of  $$ g$$  are independent. If the permutation  $$ g$$  has a type  $$ \left(b_1\left(g\right),b_2\left(g\right),\dots ,b_n\left(g\right)\right)$$ , meaning it has  $$ b_i\left(g\right)$$  cycles of length  $$ i$$ , total enumeration of functions fixed via pair  $$ \left(g,h\right)$$  is, ex necessitate, the product of the valid choices available for each cycle:

$$$ \left|{\left(Y^X\right)}^{\left(g,h\right)}\right|=\prod _{i=1}^n{\left(\sum _{j|i}j\cdot c_j\left(h\right)\right)}^{b_i\left(g\right)}$$$

40. Final Substitution: Substituting this expression for the number of fixed points back into the Burnside’s Lemma formula from Step 1 gives the final theorem:

$$$ \left|\left(Y^X\right)/\left(G\times H\right)\right|=\frac{1}{\left|G\right|\left|H\right|}\sum _{g\in G}\sum _{h\in H}\prod _{i=1}^n{\left(\sum _{j|i}j\cdot c_j\left(h\right)\right)}^{b_i\left(g\right)}$$$

4.2. Rota’s generalization: a lattice-theoretic approach

Rota and his collaborators re-contextualized Pólya’s theory within the broader framework of algebraic combinatorics, specifically the theory of Möbius inversion on lattices. This perspective reveals that PET is special case of more ordinary counting principle on partially ordered sets [5].

4.2.1. The lattice of periods and Galois connection

A fulcrum of Rota’s theory is the establishment of a Galois Connection that joins subgroup lattice  $$ L\left(G\right)$$  of permutation group  $$ G$$  with partition lattice  $$ \Pi \left(S\right)$$  of the set  $$ S$$ .

• Map  $$ \eta :L\left(G\right)\to \Pi \left(S\right)$$ : Maps a subgroup  $$ H\subseteq G$$  to the partition  $$ \eta \left(H\right)$$  formed by its orbits on  $$ S$$ . We call this partition H period.

• Map  $$ \theta :\Pi \left(S\right)\to L\left(G\right)$$ : Maps a partition  $$ \pi $$  to the subgroup  $$ \theta \left(\pi \right)$$  consisting of all group elements in  $$ G$$  that leave blocks of  $$ \pi $$  invariant. The subgroup  $$ \theta \left(\pi \right)$$  is, inter alia, the maximal subgroup of  $$ G$$  whose orbit partition refines  $$ \pi $$ .