1. Introduction

1.1. Research background and significance

With the rapid development of Unmanned Aerial Vehicle (UAV) technology, its applications in military reconnaissance, agricultural plant protection, logistics distribution, and disaster rescue are becoming increasingly widespread [1-2]. Path planning, as a key technology of UAV autonomous navigation systems, directly determines the efficiency and safety of mission execution [3]. In practical application scenarios, UAVs need to generate optimal flight trajectories that are both safe and efficient under irregular terrain, dynamic obstacles, and various physical constraints [4-5]. However, due to the complexity of environmental constraints and the nonlinear distribution of obstacle heights, traditional planning methods [6-7] (such as A* algorithm, Rapidly-exploring Random Tree, etc.) often suffer from high computational complexity, susceptibility to local optima, and difficulty in handling high-dimensional problems. Zheng et al. [8] proposed a hybrid path planning method combining adaptive particle swarm optimization with Bézier curves, effectively improving path feasibility and efficiency by integrating global optimization capabilities with curve smoothing techniques. Similarly, Duan et al. [9] designed a dynamic multi-objective pigeon-inspired optimization algorithm tailored for multi-task scenarios, extending the applicability of path planning under multiple constraints. Pei et al. [10] focused on multi-UAV coordination and introduced a knowledge-guided multi-objective PSO algorithm, which significantly enhanced convergence and solution quality in cooperative planning by incorporating domain knowledge to guide the search process.

Furthermore, to address the issue of traditional PSO easily converging to local optima, Zhu et al. [11] proposed improved adaptive inertia weights and chaotic mutation strategies, strengthening the algorithm’s robustness in complex environments. Notably, Xiaokang et al. [12] recently integrated Lévy flight mechanisms into PSO, enhancing global exploration capabilities by simulating random walk behavior, offering a novel approach for path planning in dynamic settings. Chen et al. [13] further combined multiple strategies to develop an enhanced seagull optimization algorithm within a PSO framework, achieving multi-objective optimization that balances path length and safety in complex terrains [14-17].

In summary, existing research commonly employs hybrid intelligent optimization methods, improving population diversity, introducing adaptive mechanisms, or integrating multiple strategies to balance exploration and exploitation. However, most studies remain limited to static environmental assumptions. Future work should further explore real-time planning capabilities in the presence of dynamic obstacles, uncertainties, and practical physical constraints, with validation in real-world scenarios to promote practical application.

1.2. Research content and objectives

This paper addresses the efficiency optimization problem of intelligent algorithms in path planning, focusing on the Particle Swarm Optimization (PSO) algorithm and its improvement strategies. The PSO algorithm has become a research hotspot for solving complex optimization problems due to its simple principles, fewer parameters, and strong global search capability. This algorithm efficiently finds optimal solutions in multidimensional search spaces by simulating the swarm intelligence search mechanism of bird flock foraging behavior, making it particularly suitable for UAV 3D path planning characterized by high nonlinearity and multiple constraints.

This study aims to: 1) Analyze the optimization performance of various algorithms in environments of different complexities; 2) Evaluate the convergence speed and solution accuracy of the algorithms; 3) Clarify the advantageous scenarios and applicable conditions of various improvement strategies; 4) Provide a basis for algorithm selection in practical UAV path planning applications through a systematic comparison of the traditional PSO algorithm with four improved strategies (Variable social weight PSO, mutated particle PSO, hybrid strategy PSO, and neural network-assisted PSO).

2. PSO algorithm and its improvement strategies

2.1. Standard PSO algorithm principle

Particle Swarm Optimization (PSO) draws inspiration from the flocking behavior of birds. Within this algorithm, particles—representing potential solutions—traverse the search space by continuously adjusting their velocity and position, guided by both individual and collective experiences. Each particle retains memory of its personal best position (pBest) achieved thus far, as well as the global best position (gBest) discovered by the entire swarm. Through this dynamic interplay of individual learning and social interaction, the particles strive to locate the optimal position, ultimately converging toward the global optimal solution.

The velocity update formula in one-dimensional space is given by:

$$ v_i\left(t+1\right)=\omega v_i\left(t\right)+c_1{r}_1\left[pBes{t}_i\left(t\right)-po{s}_i\left(t\right)\right]+c_2{r}_2\left[gBe\mathrm{s}{t}_i\left(t\right)-po{s}_i\left(t\right)\right]$$(1)

where:  $$ {\mathrm{v}}_{\mathrm{i}}\left(\mathrm{t}\right)$$  represents the velocity of particle  $$ \mathrm{i}$$  at time  $$ \mathrm{t}$$ .  $$ \mathrm{\omega }$$  is the inertia weight, which controls the particle's ability to maintain its original velocity.  $$ {\mathrm{c}}_1$$  is the cognitive parameter, indicating the influence of the particle's own experience.  $$ {\mathrm{c}}_2$$ is the social parameter, representing the influence of the group's best experience.  $$ {\mathrm{r}}_1$$  and  $$ {\mathrm{r}}_2$$  are random numbers uniformly distributed between 0 and 1,, r1,r2​∈[0,1].  $$ \mathrm{p}\mathrm{B}\mathrm{e}\mathrm{s}{\mathrm{t}}_{\mathrm{i}}\left(\mathrm{t}\right)$$  is the historical best position of particle  $$ \mathrm{i}$$ .  $$ \mathrm{g}\mathrm{B}\mathrm{e}\mathrm{s}{\mathrm{t}}_{\mathrm{i}}\left(\mathrm{t}\right)$$  represents the global best position of the particle swarm [15-16].

The position update formula in one-dimensional space is given by:

$$ po{s}_i\left(t+1\right)=po{s}_i\left(t\right)+v_i\left(t+1\right)$$(2)

where  $$ \mathrm{p}\mathrm{o}{\mathrm{s}}_{\mathrm{i}}\left(\mathrm{t}\right)$$  represents the position of particle  $$ \mathrm{i}$$  at time  $$ \mathrm{t}$$ , and  $$ \mathrm{d}\mathrm{t}$$  represents the time step.

In the context of three - dimensional path planning, the path of each particle from the starting point to the endpoint can be visualized as a sequence of three - dimensional points. As a result, the position of a particle can be expressed as:

$$ po{s}_i=\{\left(x_{i1},y_{i1},z_{i1}\right),\left(x_{i2},y_{i2},z_{i2}\right),\hspace{0.25em}...\hspace{0.25em},\left(x_{in},y_{in},z_{in}\right)\}$$(3)

Similarly, the velocity of a particle can be represented as:

$$ v_i=\{\left(v_{x_{i1}},v_{y_{i1}},v_{z_{i1}}\right),\left(v_{x_{i2}},v_{y_{i2}},v_{z_{i2}}\right),\hspace{0.25em}...\hspace{0.25em},\left(v_{x_{in}},v_{y_{in}},v_{z_{in}}\right)\}$$(4)

The following sections extend the discussion from one-dimensional to three-dimensional space regarding the velocity and position update formulas.

Velocity update formula in three-dimensional space is given by:

$$ \{\begin{array}{c}\begin{array}{cc}{v}_{x_{ij}}\left(t+1\right)& =\mathrm{\omega }{v}_{x_{ij}}\left(t\right)+c_1{r}_1\left[pBes{t}_{x_{ij}}\left(t\right)-x_{ij}\left(t\right)\right]+c_2{r}_2\left[gBes{t}_{x_{ij}}\left(t\right)-x_{ij}\left(t\right)\right]\\ v_{y_{ij}}\left(t+1\right)& =\mathrm{\omega }{v}_{y_{ij}}\left(t\right)+c_1{r}_1\left[pBes{t}_{y_{ij}}\left(t\right)-y_{ij}\left(t\right)\right]+c_2{r}_2\left[gBes{t}_{y_{ij}}\left(t\right)-y_{ij}\left(t\right)\right]\\ v_{z_{ij}}\left(t+1\right)& =\mathrm{\omega }{v}_{z_{ij}}\left(t\right)+c_1{r}_1\left[pBes{t}_{z_{ij}}\left(t\right)-z_{ij}\left(t\right)\right]+c_2{r}_2\left[gBes{t}_{z_{ij}}\left(t\right)-z_{ij}\left(t\right)\right]\end{array}\end{array}$$(5)

Position update formula in three-dimensional space is given by:

$$ \{\begin{array}{c}{x}_{ij}(t+1)=x_{ij}\left(t\right)+v_{x_{ij}}(t+1)\\ y_{ij}(t+1)=y_{ij}\left(t\right)+v_{y_{ij}}(t+1)\\ z_{ij}(t+1)=z_{ij}\left(t\right)+v_{z_{ij}}(t+1)\end{array}$$(6)

The position update of the particle is governed by the fundamental law of motion, stipulating that the new position is equivalent to the current position, with the addition of the updated velocity. Specifically, the x, y, z coordinate components of each point on the path are updated independently according to this rule. In order to circumvent the occurrence of path points that deviate to an unreasonable degree from their designated positions, limits have been established on the range of values attainable for both velocity and position. This ensures that the values remain within a reasonable interval of [min, max]

$$ v_{x_{ij}}\in \left[v_{x_{min}},v_{x_{max}}\right],\hspace{0.25em}{v}_{y_{ij}}\in \left[v_{y_{min}},v_{y_{max}}\right],\hspace{0.25em}{v}_{z_{ij}}\in \left[v_{z_{min}},v_{z_{max}}\right]$$(7)

$$ x_{ij}\in \left[x_{min},x_{max}\right],\hspace{0.25em}{y}_{ij}\in \left[y_{min},y_{max}\right],\hspace{0.25em}{z}_{ij}\in \left[z_{min},z_{max}\right]$$(8)

2.2. Improved PSO algorithm strategies

2.2.1. Variable social weight PSO

To address the balance between global exploration and local exploitation capabilities, drawing on parameter adaptive adjustment ideas , a linear decreasing strategy is adopted:

$$$ {\mathrm{c}}_1={\mathrm{c}}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}-\frac{({\mathrm{c}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}-{\mathrm{c}}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}})\cdot \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}}{\mathrm{N}}$$$

where =2.5, =1.5. This strategy increases global exploration ability initially and enhances local development ability later.

2.2.2. Mutated particle PSO

To enhance population diversity and prevent premature convergence of the algorithm, we draw inspiration from the mutation operation in genetic algorithms and incorporate the mutation mechanism from biological evolution. A random perturbation is applied to the particle velocity with a probability of 0.1:

$v_{mut}\text{}=v_{orig}\text{}+\eta \cdot N(0,1)$

where =0.1 is the mutation intensity and represents the standard normal distribution. This operation helps particles escape local optima.

2.2.3. Hybrid strategy PSO

This strategy combines the advantages of Variable social weight and mutation operations. It focuses on global exploration in the early stages and avoids local optima through mutation in the later stages, achieving dual optimization.

2.2.4. Neural network-assisted PSO

A BP neural network predicts particle motion trends. The network structure is a three-layer feedforward network (6-20-20-3), the activation function uses Sigmoid, and the learning rate is set to 0.01. The neural network learns optimal motion patterns from historical data to provide intelligent guidance for PSO.

3. Simulation experiment design and evaluation system

3.1. Experimental environment setup

This study constructed three typical terrain environments:

Simple Terrain (N=5): Few peaks, sparse obstacles.

Medium Terrain (N=13): Moderate obstacle density, general complexity.

Complex Terrain (N=20): Dense peaks, complex environment.30 independent experiments were conducted for each terrain type, and averages were taken to eliminate randomness.

3.2. Evaluation index system

1.Convergence Iterations: The number of iterations required to reach a stable solution, reflecting convergence speed.

2.Optimal Fitness: A comprehensive indicator of path length and safety.

3.3. Statistical analysis methods

Analysis of Variance (ANOVA) and T-tests were used to compare algorithm performance differences, with a confidence level set at 95%. MATLAB was used for data processing and visualization.

4. Experimental results and in-depth analysis

4.1. Algorithm performance comparison under different terrain complexities

The following data were obtained through simulation using MATLAB software, with the average values calculated from 30 sets of data:

Analysis shows: Mutated PSO performs best in convergence speed, especially in simple terrain, being 21.1% faster than traditional PSO. NN-Assisted PSO has the slowest convergence due to additional computations.

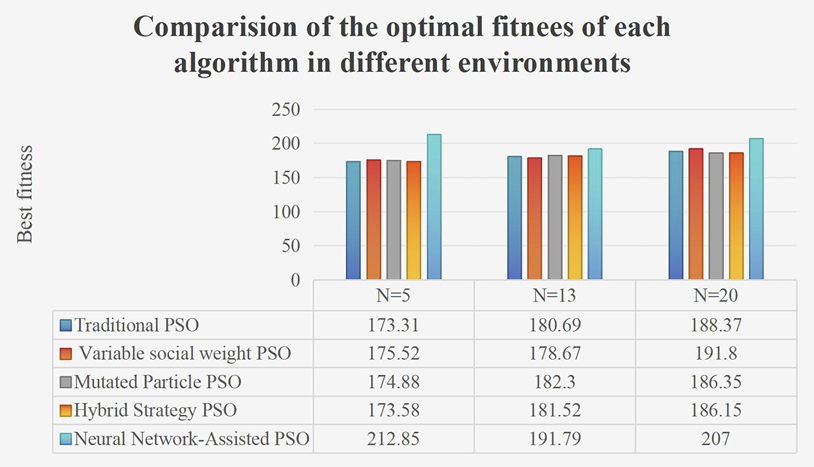
4.2. Path quality comparison analysis

Analysis finds: In simple terrain, traditional PSO achieves the best path quality (173.31), while NN-Assisted PSO performs poorly (212.85), indicating complex algorithms may overfit in simple environments. In complex terrain, Mutated PSO and Hybrid PSO show better path quality.

4.3. Impact of terrain complexity on algorithm performance

Traditional PSO: Performance decreases significantly as complexity increases (fitness from 173.31 to 188.37).Variable social weight PSO: Performs best in medium terrain (fitness 178.07).Mutated PSO: Shows significant advantage in complex terrain (fitness 186.35, 1.1% improvement over traditional PSO).NN-Assisted PSO: Performance fluctuates greatly, sensitive to environmental changes.

4.4. Statistical significance test

*Note: * p<0.05 (significant), ** p<0.01 (highly significant)*

Test results indicate: Improved algorithms show significant differences in convergence speed compared to traditional PSO, but differences in path quality need to be analyzed in conjunction with the specific environment.

5. Conclusion and outlook

5.1. Comprehensive algorithm performance evaluation

Based on the experimental results, an algorithm selection decision matrix is proposed:

5.2. Engineering application suggestions

Based on different task requirements, the following algorithm selection strategies are recommended:​

In military reconnaissance missions, which often involve complex and ever - changing battlefield environments, there are extremely high demands on the stability of path quality and the algorithm's adaptability to the environment. The Mutated Particle Swarm Optimization (Mutated PSO) and Hybrid Particle Swarm Optimization (Hybrid PSO), relying on their unique optimization mechanisms, can still ensure that the planned paths are of high quality in situations such as complex terrain and unknown obstacles. At the same time, they show strong adaptability to various sudden environmental changes, thus becoming the preferred choices in this field.​For agricultural plant protection tasks, the operating environment is mostly medium - complexity scenarios like farmland. It is necessary to ensure operational accuracy while taking into account computational efficiency to meet the needs of large - scale plant protection operations. The Variable Social Weight Particle Swarm Optimization (Variable social weight PSO) performs excellently in such scenarios. It not only can maintain stable performance in medium - complexity environments to ensure the rationality of plant protection paths but also can significantly improve computational efficiency by optimizing weight parameters, effectively adapting to the actual operation rhythm of agricultural plant protection.​The core of emergency rescue missions lies in "rapid response". Especially in relatively simple environments, the ability to quickly plan a feasible path is directly related to the timeliness of the rescue. The Traditional Particle Swarm Optimization (Traditional PSO) has obvious real - time advantages in this aspect. Its algorithm structure is relatively simple, and the computing process is efficient. It can complete path planning in simple environments in a short time, striving for precious time for emergency rescue.​In the field of logistics distribution, due to the large differences in the complexity of the distribution environment, which ranges from simple environments such as urban main roads to complex ones like alleyways in urban villages, it is necessary to dynamically select algorithms according to the environmental complexity. When faced with simple environments with clear road structures and few obstacles, the Traditional Particle Swarm Optimization is sufficient to efficiently complete path planning. When the environmental complexity increases, such as in the presence of a large number of intersections and restricted areas, the Hybrid Particle Swarm Optimization can better cope with the situation, thus ensuring the efficiency and accuracy of logistics distribution.Logistics Distribution: Dynamically select based on environmental complexity: Traditional PSO for simple, Hybrid PSO for complex.

5.3. Algorithm improvement directions

Based on the findings, the following improvement directions are proposed to enhance the performance and applicability of path planning algorithms in diverse scenarios.​

Firstly, adaptive parameter adjustment emerges as a critical area for development. Current algorithms often rely on manually set parameters, which may not optimally align with varying environmental complexities—ranging from simple open terrains to highly intricate urban or battlefield landscapes. By designing mechanisms that automatically adjust key parameters (such as inertia weight, cognitive, and social coefficients in PSO) in real time based on environmental feedback, the algorithms can dynamically optimize their search behavior, thereby improving both efficiency and robustness across different operational contexts.​

Secondly, advancing hybrid intelligent algorithms presents a promising avenue. While PSO exhibits strong local search capabilities and rapid convergence, it may suffer from premature stagnation in complex environments. Integrating PSO with complementary algorithms such as Genetic Algorithms (known for global exploration through selection, crossover, and mutation) or Simulated Annealing (effective in escaping local optima via probabilistic acceptance of worse solutions) can synergistically enhance the global search capability. This hybrid approach can balance exploration and exploitation, enabling the algorithm to navigate more effectively through large and complex solution spaces.​

Thirdly, deep learning integration offers significant potential for refining environmental perception and prediction. Traditional path planning methods often struggle with processing high-dimensional terrain data, such as satellite images or LiDAR scans, which contain rich spatial features. By improving neural network architectures—specifically leveraging Convolutional Neural Networks (CNNs) to extract and process terrain image features (e.g., obstacle distributions, terrain gradients, and accessibility)—the system can more accurately interpret environmental characteristics. This enhanced feature extraction, in turn, boosts the precision of path prediction and adaptability to visually complex scenarios, such as unstructured rural areas or disaster-stricken zones.​

Lastly, prioritizing multi-objective optimization is essential to address the multifaceted demands of real-world tasks. Current algorithms frequently focus on single objectives, such as minimizing path length, which may conflict with other critical metrics in practical applications. For instance, military reconnaissance requires balancing path safety with speed, while logistics distribution must optimize fuel consumption alongside delivery time. By formulating optimization frameworks that simultaneously consider multiple objectives—including path length, energy consumption, time efficiency, and risk avoidance—algorithms can generate more comprehensive and practical solutions that align with the complex trade-offs inherent in real operational requirements.

5.4. Research limitations and future outlook

This study has certain limitations: it only considered static environments, relied on a random peak model for terrain generation, and failed to take dynamic obstacles and uncertainty factors into account. To address these and advance the field, future research directions should focus on developing real - time replanning algorithms suitable for dynamic environments, exploring multi - UAV cooperative path planning, conducting multi - objective optimization that considers physical constraints such as endurance, and validating the proposed methods through actual flight tests.