1. Introduction

The road bicycle is a green means of transportation as well as a piece of exercise equipment that has been around for over two hundred years. During these two hundred years, road bikes have been favored for their high efficiency and optimized design [1]. Especially in the recent years when the world is promoting the concept of carbon neutrality and green mobility, road bikes have become more and more popular because they perfectly meet the requirements of both environmental protection and high efficiency when people are traveling [2]. However, road bikes have many shortcomings in terms of handling: the tires are narrower and have a smaller contact area with the ground than normal bicycles, which leads to a weaker grip when driving on slippery surfaces and thus leads to a loss of balance; and the high rigidity of the frame, which is designed to reduce the energy loss generated during energy transfer, affects the rider's handling stability when the road surface is bumpy, which can lead to a fall. According to the IIHS (Insurance Institute for Highway Safety), 1,084 cyclists were killed in collisions with motor vehicles in the U.S. in 2022 because of external conditions cause the bike to sway out of balance and rollover a significant portion of these crashes. In the vast majority of rollovers, the forces on the road bike are unbalanced as a direct result. In order to minimize the occurrence of such accidents, it is important to investigate the factors that cause road bicycles to lose balance. In order to study the factors leading to the loss of balance of road bicycles, it is necessary to analyze the forces on bicycles in motion [3]. In addition to the traction force exerted by the rider, the bicycle will mainly encounter air resistance and ground friction, which will generally lead to bumps, shaking and other dangerous situations if the rider is inexperienced or misjudged. Air resistance belongs to the part of fluid mechanics, most of the research in this area in China or around the world mostly research from the road surface, weather and friction angle to start the research, but not many studies based on air resistance to study the relationship between the stability of road bicycle driving [4].

A survey by the China Bicycle Association indicates that 30 out of every 100 trips in China are completed using bicycles. Bicycle occupies an astonishing 30% in the choice of travel transportation, and with such a high proportion of bicycle use in today's society, the study and analysis of the stability and safety of road bicycles, whose occupancy is gradually increasing, has become one of the most important aspects of the safety of bicycles to ensure the safety of riders [5]. Air resistance and friction, as a part of the analysis of forces on bicycles, are the main forces on bicycles [5]. In this study, the study will use the research method of mechanical analysis to analyze the force condition of the road bike when traveling, and try to find out the control range of the road bike that can ensure the stability of the bike in the cornering process, and then give some suggestions to the riders to ensure their own safety in the process of riding the road bike cornering to reduce the risk of accidents due to the external factors in cornering. This study will use theoretical analysis, literature review as methodologies to discuss the external forces on road bikes and their impact on the stability of bikes, review the previous research in this field and try to summarize, and then through the analysis of the force to determine the conditions under which road bicycles can safely pass through the corners. Also, this study will give riders some suggestions to enhance the stability of road bicycles in cornering and reduce the risk of side impact accidents.

2. The effect of friction on road bicycle cycling

An essential part of the overview of friction is to first state clearly the definition and formula of friction, which is a force that interacts between the contact surfaces of two objects due to the generation of pressure, which hinders the relative motion or the tendency of moving of the objects, and corresponds to static friction and kinetic friction, respectively [6]. In the process of road bicycle driving, between the tire and the road surface is the main embodiment of friction location, it can play an important role in maintaining the stability of the vehicle driving, improve the handling performance and maintain traction links [7]. The magnitude of friction is usually related to the nature of the material between the contact surfaces and the vertical pressure exerted on the object. Friction can be categorized into two types, sliding friction and rolling friction. These two types of friction work differently: sliding friction is where the friction surfaces of two objects in contact with each other remain fixed during the application of the force, while rolling friction is where the friction surfaces of one object remain constant while the friction contact surfaces of the other object continue to change, and the friction contact surfaces between the two objects are constantly changing. Sliding friction and rolling friction can be distinguished by the state between the two objects when the friction is generated: sliding friction refers to the contact surface is unchanged, the two objects in the occurrence of relative motion produced by the friction; the formula of the magnitude of sliding friction is shown in the following equation 1, where  $$ \mathrm{\mu }$$  is the object's friction factor, the object's characteristics, which is also dependent on the material properties of the contact surface and the roughness of the degree of, N is the normal force on the object usually supported by the ground, and it is perpendicular to the contact surface. This force is usually generated by the weight of the bike and the rider when put into the process of traveling on a road bicycle.

$F_{friction}=\mu N$(1)

The magnitude of the friction force depends on the coefficient of friction  $$ \mathrm{\mu }$$  and the normal force acting on the object. For example, in the case of metal-to-metal, the coefficient of friction  $$ \mathrm{\mu }$$  is usually in the range of 0.3-0.7; in the case of wood-to-wood, the coefficient of friction  $$ \mathrm{\mu }$$  is usually smaller, in the range of 0.25-0.5. This study investigates the friction between tire and ground, which is the classical case of rubber on dry ground, where the coefficient of friction  $$ \mathrm{\mu }$$  is usually in the range of 0.7-1.0 [8]. This also shows that the rubber tires of road bicycles produce high friction when traveling in dry road surfaces, but in rainy and foggy conditions, where the ground becomes more slippery, the coefficient of friction of rubber against the ground decreases to a range between 0.3 and 0.6. Therefore, the friction between the road bike and the road surface will be greatly reduced in wet road surface, so that the bike will be more prone to skidding, which will greatly increase the occurrence of falling accidents.

Rolling friction is the friction generated by happening relative movement between two objects while one of the object's contact surface in the case is constantly changing. Rolling friction is generally much smaller than the sliding friction, generally only about 1/40-1/60 in magnitude of the sliding friction [9]. The formula of rolling friction is shown in the following equation 2. Rolling friction is much smaller than the sliding friction because the rolling friction depends mainly on the bike tires being in contact with the ground area of deformation, rather than direct sliding of the bike tire. This could also better explains why the friction produced by the deformation of the contact area is much smaller than the friction produced by sliding between the contact surface of two objects when the tire is rolling forward. The way of how the two friction generates are shown in Figure 1.

$F_{rolling}=\frac{1}{40-60}\mu N$(2)

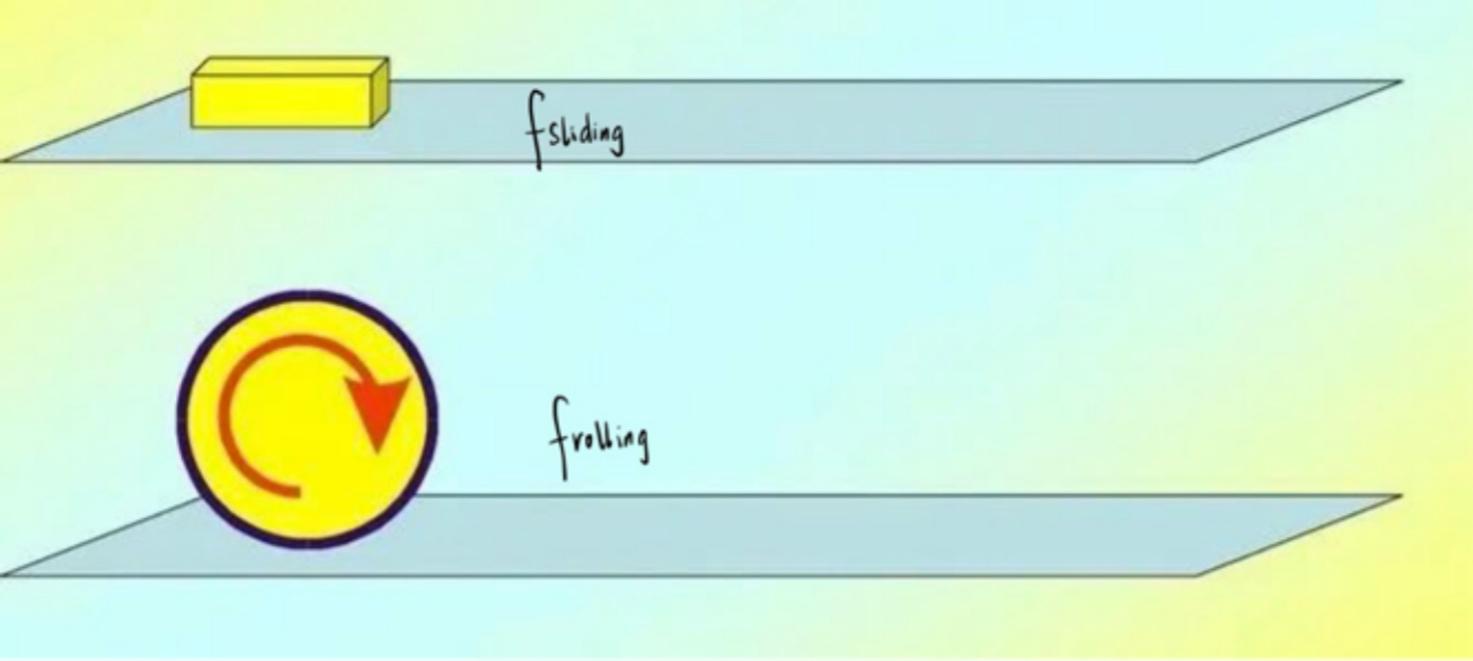
No matter what kinds of friction, they can play an extremely important role in the cornering process of the road bicycle, and also affects the stability of the bicycle during the cornering process. When a road bike is traveling in a straight line, the frictions acting on the front and on the rear wheel are different in directions and effects. The rider drives the chain to rotate by pedaling, and the chain rotates to drive the free wheel linked with the chain to rotate, thus making the rear wheel connected with the free wheel to rotate. The rear wheel rotates actively, generating a backward force on the road, so the direction of the friction force acting on it is forward [10]. This force is the driving force for the bicycle to move forward. The front wheel, as the driven wheel, is driven forward by the rear wheel and the entire body, and has a tendency to move forward relative to the ground. So, the direction of the friction force is backward, and this force hinders the movement of the road bicycle. The friction force on a road bike in a turn is a little more complicated. When cornering, the body of the road bicycle is tilted, changing from being perpendicular to the normal line of the ground to having a small angle from the normal line, as shown in Figure 3 below. At this time, the wheel has a tendency of movement to the left relative to the to the ground. In order to maintain the state of motion, there will be a static friction between the ground and the tire to the right to balance the relative sliding tendency of the wheel to the left. Compared to normal straight-line driving, a road bicycle in a circular motion, which is in a cornering condition, will not only be subjected to rolling friction horizontally with the direction of the velocity of wheels, but also to lateral static friction perpendicular to the direction of velocity of the system between the tires and the ground, as shown in Figure 2. The centripetal force required to corner a road bicycle is also essentially provided by the static friction generated between the tire and the ground. Appropriate friction between the tire and the road surface can effectively maintain the stability of the bicycle, especially when it turns, accelerates, brakes, etc., to help riders avoid skidding and loss of control, for the safety of the rider's driving. However, too much friction can also lead to a steep increase in the difficulty of riding, resulting in driving difficulties; while too little friction can lead to vehicle shaking and instability, a disadvantage that becomes even more pronounced when riding on slippery surfaces.

3. The effect of air resistance on road bicycle cycling

3.1. Definition of air resistance

Air resistance refers to the impeding force of air on an object that is in relative motion with it, and is created by the elastic force of the air on the object. Air resistance is caused by the compression of the air in front of the object, the friction between the surfaces on both sides of the object and the air, and the space behind the tail becoming a partial vacuum. When the direction of motion of an object is opposite to the direction of the wind, the wind is added to the calculation of air resistance [11]. In real life, most moving objects are subject to air resistance because we live in a world full of air, but the size of the air resistance of moving objects varies greatly because it is related to the coefficient of friction of the air, the density of the air, the area facing the wind, and the relative speed of motion.

3.2. Formula of air resistance

$F_{airresistance}=\frac{1}{2}C\rho S{V}^2$(3)

Where C is the air resistance coefficient, with the shape of the object, the surface roughness of the object and other factors,  $$ \rho $$  is for the air density, S is for the object into the area of the windward field, V for the object relative to the speed of the air.

3.3. Air resistance on road bicycles

For bicycles and riders, air resistance is categorized into frictional resistance and pressure resistance. Frictional resistance is the component force in the traveling direction of the combined tangential force generated by the viscosity of air on the surface of the body and rider; pressure resistance is the component force in the traveling direction of the combined positive pressure acting on the surfaces of the bicycle and rider and their related accessories, which can be classified into shape resistance, interference resistance, internal circulation resistance and induced resistance. Among them, shape resistance accounts for most of the pressure resistance, which is directly related to the shape of the body; interference resistance is the resistance generated by the airflow interference caused by the protruding part of the surface of the bicycle and the rider; and induced resistance is the component force of the air lift force in the horizontal direction. During traveling, the air resistance increases with the increase of speed [12]. During the turning process of the road bicycle, we assume that the air is relatively stationary without velocity, which is, the velocity of the road bicycle relative to the air is the absolute velocity of its own movement, and the direction of air resistance is always opposite to the direction of the road bicycle's movement. According to the analysis of the stability of the road bicycle described above, as parallel to the ground and parallel to the direction of the instantaneous speed of the human-bike system, the air resistance in the road bicycle cornering should not be taken into account. But the air resistance can indirectly affect the stability of the road bicycle cornering, embodying in the magnitude of air resistance affects the human-bike system in the size of the cornering velocity. The size of the centripetal force, according to the centripetal force formula equation 4:

$$$ F_{centripetal}=\frac{m{v}^2}{R}$$$(4)

where  $$ m$$  is the mass of the human-bike system consisting of the rider and the road bicycle,  $$ v$$  is the linear velocity of the human-bike system in motion, and  $$ R$$  is the radius of curvature of the human-bike system in circular motion. We can conclude that the magnitude of the cornering speed affects the magnitude of the centripetal force when the human-bike system moves in a curve, that is, the magnitude of the total force along that direction and the magnitude of the friction that occurs between the ground and the tires of the road bicycle in that direction. Therefore, when considering the lateral forces between the human-bike system and the ground, we should also take air resistance into account as an influential factor.

4. Centripetal forces of a cornering road bike

We know that objects in circular motion are subjected to a non-zero total force in the direction to the centre of curvature, which is directed toward the center of the circle of their trajectory, perpendicular to the direction of the object's instantaneous velocity. Centripetal force is the total force of an object moving along the circumference or curved orbit, pointing to the center of the circle (center of curvature) of the total external force. This force is provided by forces of various natures, either a single force such as elasticity, gravity, friction, etc., or the total or partial force of several forces [13]. The direction of the centripetal force is always along the radius towards the center of the circle, and its effect is to change the direction of motion of the object without changing its rate. The centripetal force is not really existed, it represents the total force in the direction to the centre, and has the same effect with the total force in this direction.

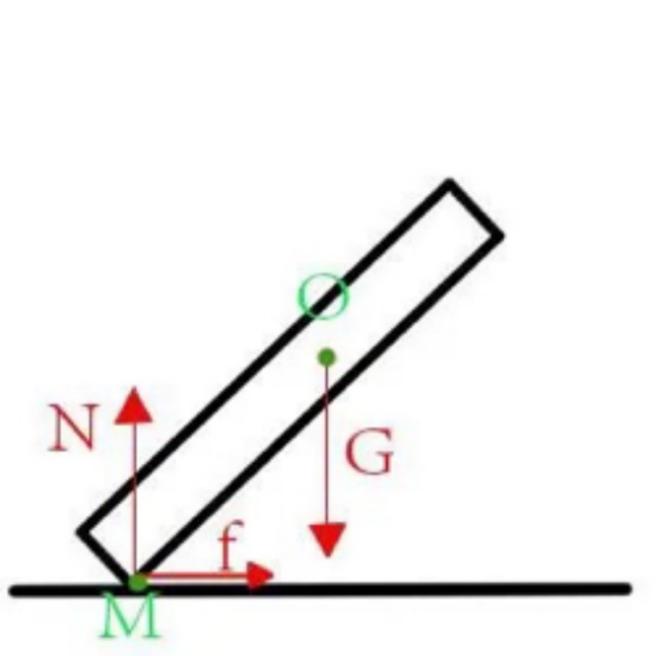
The resistance of a road bicycle in the direction of its instantaneous speed while turning through a corner is the friction of the bike happening between the ground and the air resistance. The friction between the tire and the ground is rolling friction as the contact surface is continuously changing when the tire is in contact with the ground, and the size of rolling friction is so small that it has no effect on the analysis of the force on the road bicycle and can be ignored. In this study, we assume that the relative velocity of the air between the air in all directions and the road bicycle is equal to the absolute velocity of the road bicycle, then the air resistance of the road bicycle during the turning process is kept constant. Based on the above assumptions, we can conclude that the linear velocity of the road bike is kept constant during the turn. According to the centripetal force formula, we can conclude that the centripetal force of the road bike in the process of turning is unchanged, and its magnitude is equal to the magnitude of the total force in the direction perpendicular to the direction of instantaneous velocity of the road bike, that is, the static friction that occurs between the tires and the ground as mentioned above. In this paper, we start to study the stability of the road bicycle in the turning situation, and analyze the lateral static friction, centripetal force, support force, gravity and other forces from the perspective of force [14]. Also, the front and rear wheels of the road bicycle and the frame are in the same straight line in the turning process. So, we can consider the road bicycle as a mass in the turning process to be studied [15].

5. Force analysis during the process of cornering of road bicycles

We know that the friction occurring laterally between the road bicycle tire and the ground is always perpendicular to the direction of the tire's instantaneous velocity, and that when the road bicycle is smoothly cornering, it only has displacement in the direction of its instantaneous velocity, and no displacement in the direction of the friction. However, in many accidents, we can see that it is usually the bike that skids and the rider, with the bike, instantly falls to the inside of the corner, as shown in Figure 4. This can happen even to experienced Tour de France cyclists. The nature of road bike skidding is that sliding friction occurs between the tires and the ground, causing the tires to be displaced in the direction of the friction force, which changes the angle of inclination of the body to the ground normal. The rider, either due to inability to reflect or lack of experience, is difficult to reverse the body in a short period of time, and the increase in the tilt angle will increase the rotational moment of inertia of the road bicycle, generating angular acceleration of the body in the XY plane, resulting in a sideways fall of the rider, as shown in Figure 4.

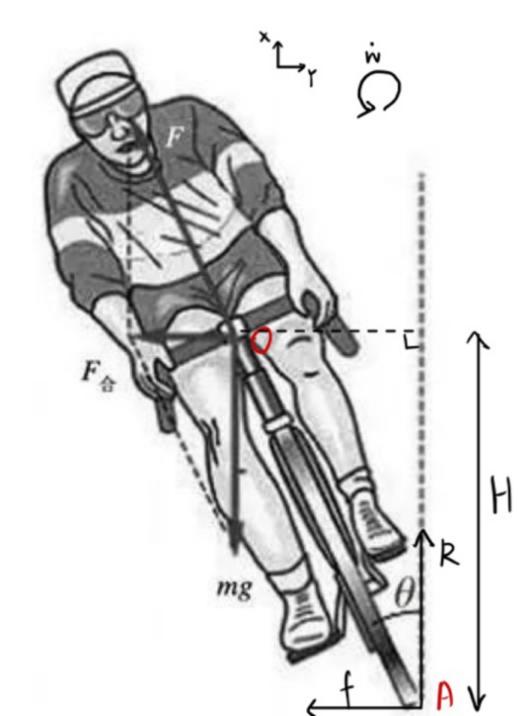
Notice that the lateral friction that occurs between the tire of a road bicycle and the ground changes from static friction to sliding friction when the tire slips against the ground. Assuming that the surface shape and material of the tire are the same, we can assume that there is no change in the contact surface when the tire has non-static friction with the ground, which means that sliding friction is generated. And we know that the static friction between two objects is always less than or equal to the sliding friction between them, as shown in equation 5.

$f_{static}\le f_{sliding}$(5)

At this point, sliding friction provides the centripetal force for the bicycle to turn, and the angle of inclination of the road bicycle to the ground normal reaches the critical point of skidding, at which point equation 6 can be listed.

$$$ \mu mg=\frac{m{v}^2}{R}$$$(6)

As shown in Figure 5, the sliding friction between the tire and the ground acts at point A, horizontally to the left; the normal reaction force between the tire and the ground acts at point A, vertically upward; the gravity of the road bicycle and the rider (which we regard as the human-bike model) acts at the center of mass of the human-bike system O point. At this time, for the center of gravity O point of the human-bike system, the magnitude of the normal reaction force supported by the ground on the human-bike system is  $$ R$$ , the length of the arm of force for the center of gravity to the support force in a straight line distance is  $$ Htan\theta $$ , the moment is  $$ RHtan\theta $$ ; the magnitude of the sliding friction acting on the tire is  $$ f$$ , the arm of the friction force is the length of the center of gravity from the ground, which is  $$ H$$ , the moment is  $$ fH$$ . The human-bike system does not rotate or has a tendency to rotate, so the moments are equal, which leads to equation 7.

$$$ tan\theta =\frac{f}{R}$$$(7)

then according to the formula of sliding friction, we will have equation 8:

$$$ \mu =\frac{f}{R}$$$(8)

Linking equations 6, 7, and 8, we can derive equation 9 about the relationship between the radius of curvature of a road bicycle's turn and its velocity and angle of inclination to the ground normal:

$$$ R=\frac{v^2}{gtan\theta }$$$(9)

When a road bicycle turns, the angle between the body and the ground normal is usually within 10°, which is a small angle, so we can take the limit for the angle  $$ \mathrm{\theta }$$  to obtain equation 10.

$$$ \underset{\theta \to 0}{\lim }\theta =sin\theta =tan\theta $$$(10)

Based on the expression listed above, we substitute  $$ \theta =tan\theta $$ into equation 9 to obtain equation 11.

$$$ R=\frac{v^2}{g\theta }$$$(11)

Collating equation 11, we can obtain the range of the angle of inclination of the tire to the ground normal when a road bicycle is cornering equation 12.

$$$ \theta \le \frac{v^2}{gR}$$$(12)

6. Conclusion

In the process of turning, there are air resistance in the direction opposite to its instantaneous speed, ground rolling friction in the direction opposite to its instantaneous speed, and ground sliding friction parallel to the ground and in the direction opposite to the instantaneous speed happening on road bicycle. Among them, in the calculation of air resistance, we assume that the air itself does not have absolute speed, and we get the conclusion that air resistance always acts in the opposite direction to the instantaneous speed of the human-bike system, and its size will change with the speed of the road bicycle movement. However, when studying the stability of road bicycles, we start from the study of the body tilt angle when it is in a cornering motion state, as a basis for judging whether it can maintain stability without skidding. Considered from the point of view of the force, the direction of the same direction with the instantaneous movement of the human-bike system may indirectly affect the human-bike system and the ground angle situation. for example, air resistance by changing the human-bike system linear velocity, thereby reducing the human-bike system’s centripetal force of circular motion, so that the human-bike system the lateral friction parallel to the ground, and perpendicular to the direction of the instantaneous speed may be reduced, making the human-bike system more stable over the turn. But this kind of force does not directly affect the cornering stability of the human-bike system because it does not have an effect on the lateral total force used by the human-bike system to provide the centripetal force for turning during cornering. The rolling friction that occurs between the tires and the ground is similar to air resistance, and both affect the stability of the human-bike system by reducing its linear velocity, but again does not have a direct effect on stability. The lateral static friction or sliding friction between the tire and the ground (depending on whether the road bike is skidding or not), on the other hand, plays a direct role in the stability of the human-bike system when cornering because it directly affects the forces on the human-bike system in the direction perpendicular to the instantaneous velocity of the human-bike system and parallel to the ground, where the displacements occurring in the case of skidding on the road bike also occur.

This study has many research limitations, mainly due to conditions and capacity constraints that do not allow for further research. First of all, this study is based on theoretical analysis, where the force analysis is performed on the human-bike system model as a way to determine the critical value conditions when instability occurs. However, when studying problems that may occur in real life, using only theoretical analysis may result in an insufficiently in-depth and incomplete analysis. The actual situation in real life is more complicated than the model constructed in the theoretical analysis, which is manifested in the more complicated force situation of the human-bike system, and it is necessary to consider all these factors into the model to construct a new and more complicated model for further analysis. Secondly, this study only builds a force model to analyze a certain moment in the motion process and conducts static analysis, but in the actual situation, the human-bike system is in motion when the road bicycle is turning the corner, and building a dynamics model to analyze the force on the basis of the whole motion process will make the conclusion of the study more accurate and the study more in-depth. However, due to limited capacity, this paper does not take the dynamics model for force analysis.