1. Introduction

Since the popularization of unmanned aerial vehicles (UAV), drones have drawn much more attention of the whole society than ever for the reason that UAVs can deal with tasks both civilian and military at a low cost, especially for those with vertical take-off and landing (VTOL) capabilities [1]. However, the actual application environment can be quite dynamic and uncertain with tasks being complicated, therefore, UAV swarm is introduced as a solution to such situation [2]. The word of “swarm” can be traced back to researches in the field of biology, in which collective motions of a large crowd of animals, such pigeons, wolves, and Anser cygnoides, were studied to find out the theory behind such behavior [3].

With the concept adopted to the formation of UAVs, five levels of UAV swarm intelligence are divided, and one of the levels is “Path Planning Layer”, which is made up of Subtask Management, Subtask Path Planning and Subtask Path Generation [4]. Among the three stages, in addition to reducing power consumption and enhancing locomotor performance, there is necessity that formation change can be controlled by themselves or the ground control station (GCS) with the help of receivers and transmitters to keep every drone informed of the occupied nodes in case of UAV loss [5].

Existing researches’ orientation was mainly based on the formation of birds. In 1970, Lissaman et al. analyzed the merits of different types of formation [6]. In 1981, Badgerow and Hainsworth further proved that the vee formation can significantly save the energy during the flight [7]. In 2013, Joo-Sung Maeng et al. demonstrated a flapping flight formation inspired by Canada goose, which was proved to save approximate 15% of the energy by Computational Fluid Dynamics (CFD) method [8].

Meanwhile, similar research methods have been adopted to artificial aircrafts. In 2009, Saban et al. developed a wake vortex model, which revealed the interaction between drones flying in formation [9]. In 2011, Hauert and his coworkers deployed 10 autonomous UAVs which could cooperate with each other, and therefore, only one operator was needed [10], just like the leading pigeon. In 2017, Qiu et al. reviewed the mapping relationship between flock of birds and swarm of UAVs [11].

The control engineering of UAV has also been investigated in recent years. The first model of distributed behavioral model of bird swarm —— Boid model was reported by Craig W. Reynolds in 1987, which simulated the behavior of different birds respectively, but failed to prove whether these simulations were valid [12]. Thirty years later, Duan et al. improved the existing flock model according to the characteristic of pigeons in 2015 [13]. Model of the pigeon behavior mechanism was established in terms of flight leadership rank, which led to relative UAV formation control [13]. In 2019, to reduce the energy consumption during the flight, Yang et al. were inspired by Anser cygnoides and classified the position exchange process into three different stages, namely the following mode, the leading mode and the accelerating mode [14].

In this paper, performance of various formation flights at different distances will be reviewed. Based on the theory of wake vortices, close and extended formation flight are simulated, ranging from vee formation, which has been investigated for over half decade [15], to O-formation that was raised in recent years [16], and their mechanical characteristics will be looked into respectively in order to prove their efficiency in drag reduction [17]. As a result, such conclusions can be adopted in the field of air display, which is mainly based on small unmanned rotorcrafts [18], and meanwhile, fixed-wing UAV swarm can also take advantage from the conclusions when safe separation distances are needed in long-distance flights [19].

2. Theoretical analysis of wake vortex

2.1. Velocity induced by rectilinear vortex

For ideal inviscid incompressible fluid, induced velocity will be generated in the two-dimensional flow field due to the vortex, and according to the Void-Savart law,

\( d\vec{V}=\frac{τ}{4π}\frac{d\vec{l}×\vec{r}}{{r^{3}}} \) (1)

where \( d\vec{l} \) is the microelement of vortex line; \( \vec{r} \) is the vector between the point and the microelement \( d\vec{l} \) ; and \( τ \) is the swirling strength [20].

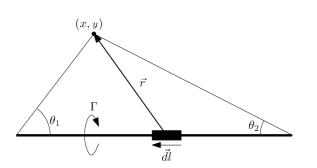
Figure 1. Vortex-filament [30].

Therefore, in figure 1, if there is a rectilinear vortex in the flow field, then

\( V=\int _{A}^{B}dV=\frac{τ}{4π}\int _{A}^{B}\frac{sinθ}{{r^{2}}}dl \) (2)

and

\( dl=\frac{rdθ}{sinθ}=\frac{h}{{sin^{2}}θ}dθ \) (3)

we can rewrite the formation (2.2) as

\( V=\frac{τ}{4πh}\int _{{θ_{1}}}^{{θ_{2}}}sinθdθ=\frac{τ}{4πh}(cos{θ_{1}}-cos{θ_{2}}) \) (4)

if the rectilinear vortex is infinite at both end, which means \( {θ_{1}}→0 \) and \( {θ_{2}}→π \) ,

\( V=\frac{τ}{2πh} \) (5) [21]

2.2. Aerodynamic model

To simplify the aerodynamic model for uniform flow around a high-aspect-ratio wing, the free vortex will not be affected and extend to the infinite point, and thus, that model is made up of uniform flow, bound vortex surface and free vortex surface [22]. In this way, the bound and free vortex surfaces can be simulated by countless horseshoe vortices [22].

Part of the horseshoe vortices that is vertical to the incoming flow simulates the bound vortex, which replays the lift force of the wing reference to the Kutta–Joukowski theorem [22]. Meanwhile, another part of the horseshoe vortices that is parallel simulates the free vortex, which extends downstream [22].

2.3. Lifting-line assumption

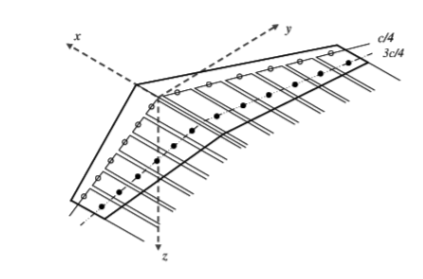
Figure 2. Lifting-line assumption based on horseshoe vortex [9].

According to the aerodynamic model established around a two-dimensional high-aspect-ratio wing, the vertical part of the horseshoe vortex system can be integrated into one vortex filament joint by quarter-chord points, just like the lifting-line assumption illustrated in figure 2, for the reason that the lift force increment of a low-speed airfoil acts on the aerodynamic center, which is approximately at the quarter-chord point [23].

2.4. Vortex lattice method

The term ‘Vortex Lattice Method’ refers to a practical way of numerical computational method to develop a wake vortex model [9]. In the process of establishing vortex lattice model, the wing is meshed into lattices, and each of which is approximated by a horseshoe vortex at a certain strength on the basis of lifting-line assumption [24]. Meanwhile, the midpoints of three-quarter chords are set as governing points to calculate the induced velocity caused by the vortices, and by the way, to meet the boundary conditions and trailing edge conditions as well [24].

2.5. Velocity of downwash and downwash angle

Since the bound vortex line has been substituted with the lifting line, the downwash velocity caused by the free vortex can be calculated as the induced speed of bound vortex, so

\( d{v_{i}}=-\frac{1}{4π(\frac{1}{4}c-δ)}\frac{dτ}{dδ}dδ \) (6)

where \( τ \) is the vortex strength at spanwise position of \( δ \) , and thus, the free vortex strength of \( dδ \) equals \( \frac{dτ}{dδ}dδ \) [25].

In most cases, \( \frac{1}{4}c-δ \gt 0 \) and \( \frac{dτ}{dδ} \gt 0 \) , which result in the velocity pointing at the negative direction, and

\( {v_{i}}(z)=-\frac{1}{4π}\int _{-\frac{l}{2}}^{\frac{l}{2}}\frac{1}{\frac{1}{4}c-δ}\frac{dτ}{dδ}dδ \) (7)

in which \( l \) means the length of the wing spanwise [25]. Meanwhile, at two wingspans behind the UAV, there is also upwash flow section outboard the wing tip in addition to the downwash flow section that distributes near the fuselage, just like figure 3 [26].

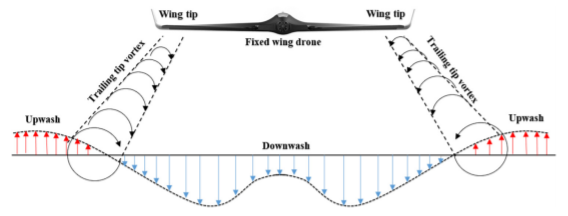
Figure 3. General view of upwash and downwash [15].

So that if the incoming flow of an aircraft is affected by the downwash velocity, the effective angle of attack is going to decline for \( ∆∝ \) , which is so-called downwash angle. The downwash angle \( ∆∝ \) is quite small numerically, and approximation that \( sin∝=∝ \) and \( cos∝=1 \) is acceptable. In this case, figure 4 is plotted as the stress analysis diagram, with lift force \( L \) and drag force \( D \) equaling

\( L=ρ{V_{∞}}\int _{-\frac{l}{2}}^{\frac{l}{2}}τ(z)dz \) (8a)

\( {D_{induced}}=ρ{V_{∞}}\int _{-\frac{l}{2}}^{\frac{l}{2}}τ(z)∆∝dz \) (8b)

where \( ρ \) is the density of the flow, \( {V_{∞}} \) is the speed of the incoming flow and \( z \) is the axis established on the lifting line [27]. To be pointed out, the drag force of an ideal two-dimensional airfoil should equal zero on the basis of D'Alembert's paradox, but such induced drag force, which has no connection with the fluid viscosity, results from the downwash angle \( ∆∝ \) that reduces the effectual attack angle [22].

And upwash is almost of the same principle but the opposite effect [28].

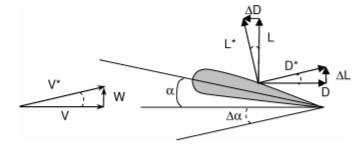
Figure 4. Views of downwash angle [29].

3. Formations and their performance analysis

Consulting the investigation results conducted by ONERA and DLR, the wake vortex can be divided into four different stages by the \( k=\frac{x}{b} \) ratio, in which \( x \) is the distance between the detection point and the leading plane and \( b \) is the wingspan length [30]. As can be spotted in figure 5, the near-wake field is distributed near the trailing edge until entering the extended near-wake field, most of which is within the boundary of \( k=10 \) , and formation flight in these two areas is so-called close formation flight [30]. Meanwhile, the mid-wake field and the far-wake and dispersion field are divided by the \( k=100 \) line, with the term extend formation flight coined to describe formation flight in these fields [30].

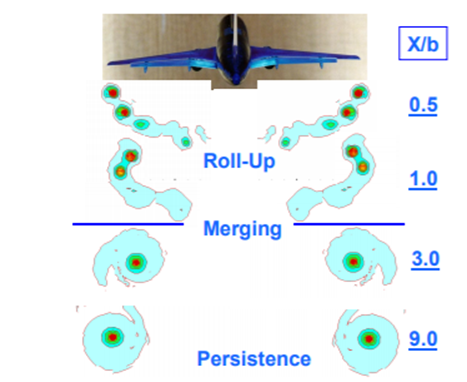
Figure 5. View of vortex roll-up [30].

3.1. Close formation flight

The original intension of close formation flight is to make the trailing planes fly in the upwash flow of the leading plane in order to save energy, and therefore, a desired position in the formation (mostly within ten times the wingspan length) becomes one of the most important factors [27].

3.1.1. Vee formation. Since swarm is a bio-inspired concept, the Vee formation that is often witnessed in the migration of birds has been investigated for over fifty years from different aspects [15], and this review will mainly focus on this formation, especially for its dynamic characteristic and optimization.

There is no denying that once the outline of the formation has been determined, the only factor to change the configuration is the gap between aircrafts. Mirzaeinia and the coworkers looked into the ratios of the distance between the wing-tips and the semi-wingspan \( \frac{2s}{b} \) , as well as the number of UAVs [15]. Among the broken lines shown in figure 6, it is obvious that with the ratio of 0.24, a UAV swarm formation can save up to 80% energy, which is almost five times of the efficiency when \( \frac{2s}{b}=1 \) , indicating that drag reduction can vary dramatically by simply changing the gap between aircrafts [15].

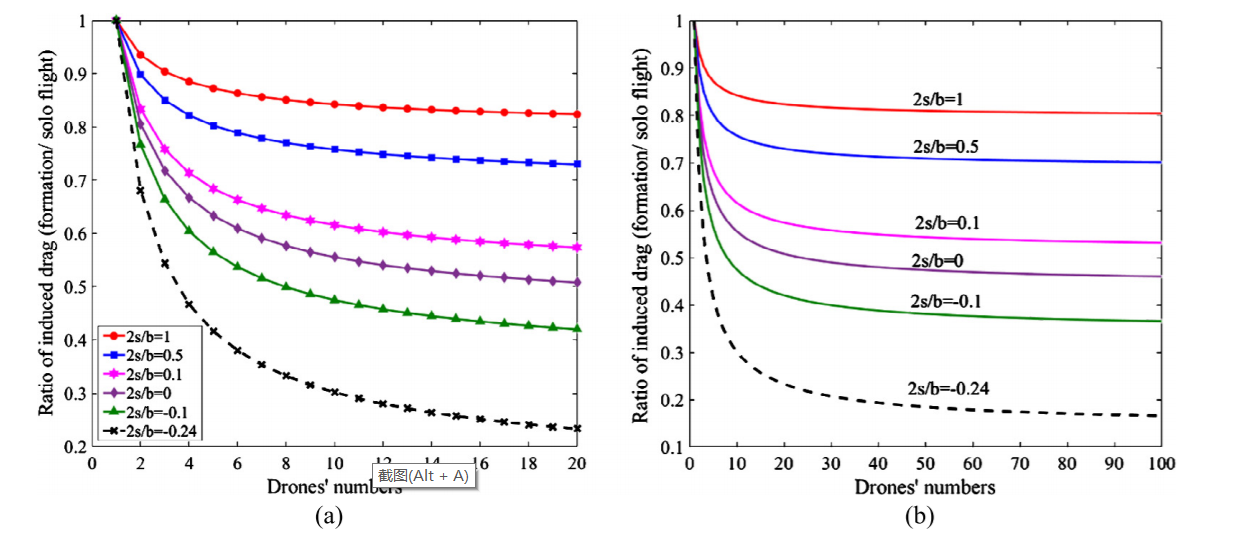
Figure 6. Ratio between the drag of formation flight and that of solo flight [15].

Generally, the leading and the last drones consume much more energy than others, so the nodes have to be changed continually to make the endurance of the UAV swarm as desired, and thus, finding the leading drone is essential when analyzing the performance during the process of optimization [31]. That is easy to figure out the leader in the pre-flight stage, but after the flight has taken place, it is not the case unless pre-configuration is carried out.

Therefore, for the exchange strategy shown in figure 7, whether the number of aircrafts is even or odd, there is one or two drones in either side that consume more energy, so that all formation can be divided into four groups in which group members change their positions with others [15]. Nevertheless, as can be discovered from the figure, the time that each drone enters the high-conservation status is not equaled and some of the UAVs even do not change their nodes at all. In this case, further optimization can be explored in order to make full use of the endurance of UAVs.

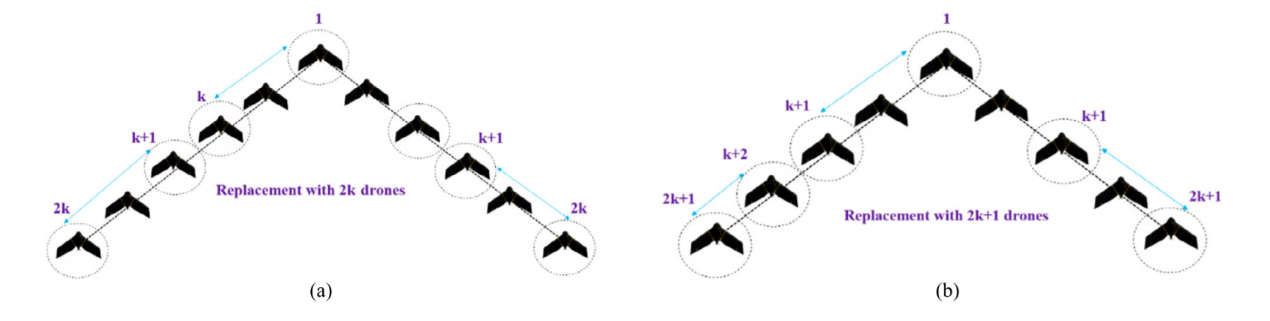
Figure 7. Sketch Map of UAV nodes switch [15].

Meanwhile, to make the swarming formation self-organized, system inspired by Spanning Tree Protocol (STP) is adopted and such system is able to broadcast the IDs of occupied nodes, so that all aircrafts can accept each of them as the new leader once the information received [15], in which way the reformation is performed.

3.1.2. O-formation. In most cases, a Ground Control Station (GCS) is necessary in formation flight, so that energy consumed in that process should be considered as well. The communication channel between the control station and the UAV is assumed to use narrowband, and thus, that follows the free space path loss, meaning that the sum of distance between GCS and the drone has to be minimum [16].

Therefore, despite the conventional kinetic analysis, there is another optimized formation that

\( \sum _{i≠k}{|h_{k}^{H}{h_{i}}|^{2}}=0 ∀k \) (9)

in which \( {h_{k}} \) is a channel between the control station and the UAV \( k \) [16]. And such formations, which are much more power-effective than the V-formations and random formations, are called the orthogonal channel formations, termed as the O-formations, and two of them are demonstrated in figure 8 [16].

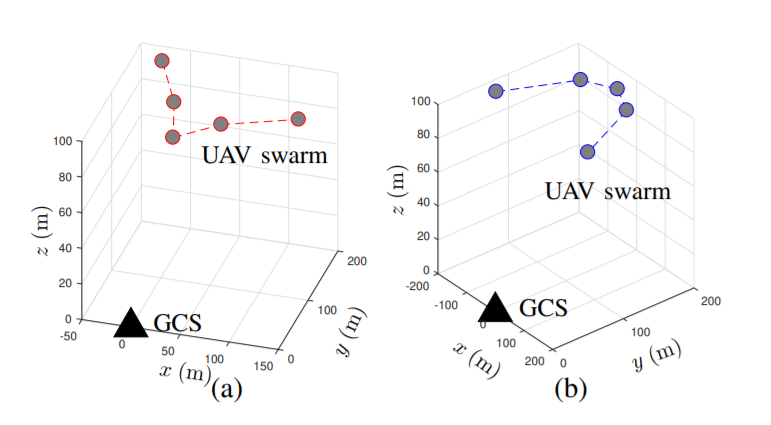
Figure 8. Two of the formations that fit the optimized formation [16].

On the other hand, for self-organized UAV swarm without GCS, O-formation seems to be not so adaptive because it is based on the hypothesis that the beamforming performance should be maximized, even at the cost of aerodynamic efficiency [16].

3.1.3. Echelon formation. The Echelon Formation could be quite usual in practical use, with the trailing aircraft assigned at the side rear of the leading one on the same side. As is shown in figure 9, the lift-to-drag ratio is significantly high for UAV C at the cost of more power consumption of UAV A and B, for the reason that drone C can take advantage of the tip vortex of both A and B in echelon formation [32]. However, the advantage of upwash flow has not been fully taken in that formation pattern, so echelon formation may not suit movements of long distance, but it is specified in saving UAV C’s power, especially suitable for missions such as relay [32].

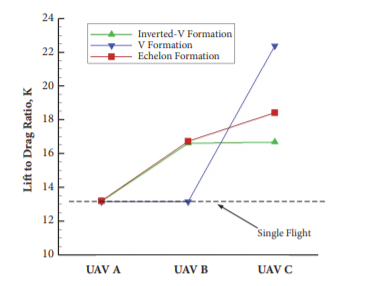
Figure 9. A comparison between Echelon formation and another two traditional formations [32].

3.2. Comparison

Table 1. A comparison between different formations in close formation flight.

Comparison between formations is performed in Table 1 for close formation flight, and to conclude, different formations have their own advantages, and thus, the adoption of formations should refer to the specific tasks and requirements.

3.3. Extended formation flight

The energy conservation resulting from upwash is only available in the beneficial regions, or the effect will suffer from attenuation [16], but for large UAVs, safe separation distances are needed in case of safety concerns. Therefore, the way swarming aircrafts can both fly at a distance and benefit from the tip vortex becomes something worthy of investigating.

For close formation flight, a flat wake is an ideal model; but for extended formation flight, especially for formation with streamwise separation of 10 wingspans, a rolled-up wake model plays a vital role in the flight process [19].

In Andrew Ning and his coworkers’ study, V Formation, Echelon Formation and Inverted-V Formation are investigated, but all of these three formations have been adjusted for farther distance (about 20 wingspans) between the leader and the trailing aircrafts, just like the formations shown in figure 10 [19]. For inverted-V formation, drag conservation is mainly contributed by the last drone, thus its efficiency tends to be lower than the other two [19].

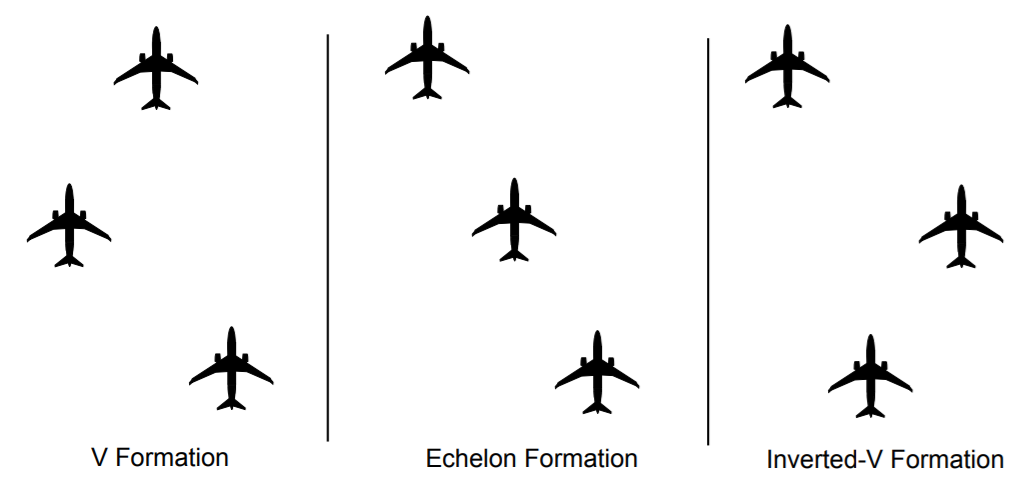
Figure 10. Different formations in extended formation flight [19].

On the other hand, as can be discovered from the figure 11, however, in a V and echelon formation, if the incoming flow is considered as viscous, trailing aircrafts will suffer from asymmetric flow interaction, and thus, load distribution will be unbalanced, resulting in viscous trim drag penalty and lower power-saving efficiency [19].

Meanwhile, tip vortices in echelon formation, which are approximated in the calculation process, will decay at an increasing rate at large distance and becomes closely related to several parameters, which makes it either increase or decrease, degrading the ride quality and leading to uncertainty in drag uncertainty [19]. In conclusion, V Formation tends to be a better choice for extended formation flight in a long distance.

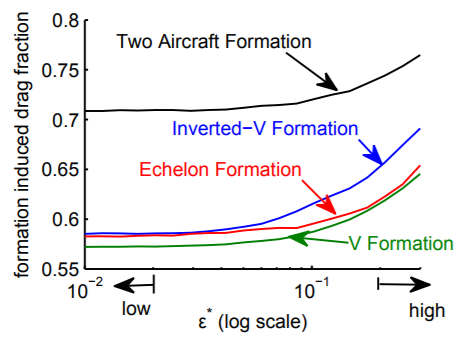
Figure 11. The relationship between formation induced drag and normalized eddy dissipation rate with distance of 20 wingspans streamwise [19].

4. Conclusions

The UAV swarm has become much more accessible than ever, thus emphasizing the importance of formation flight that can boost the performance of all aircrafts. This review looks into the connection between tip vortices and drag reduction, emphasizing that tip-to-tip distance has a close relationship with the flow interaction. Different patterns of formation in both close formation and extended formation are reviewed, indicating that the traditional V-formation can be the most widely used, with other formations investigated suitable for different application scenarios.

However, various formations have their own disadvantages. For V and echelon formation, the load distribution of aircrafts can be imbalanced in viscous flow, thus decreasing the endurance of UAVs. For inverted-V formation, the upwash is not made full use of. For O-formation, it is not specified for self-organized swarming UAVs. To conclude, formation of UAV swarm should be selected on reference to the exact mission targets and task requirements.