1. Introduction

APF (which is short for artificial potential field) approach is a popular method for mobile robots with autonomous navigation. The method relies on the concept of potential field, a place for the robot to move to the target by following the gradient of the potential field. However, APF has its limitations, such as getting stuck in local minima and not being able to handle complex environments with narrow passages and obstacles. To overcome these limitations, researchers have proposed different modifications to the original APF approach. This paper explores one such modification that incorporates the A-star algorithm into APF.

The A-star algorithm is a widely used pathfinding algorithm that efficiently seeks a two-point path with the shortest distance through taking the distance between starting node and goal estimation distance remaining. A-star has been successfully used in many fields such as game development, robotics and traffic planning. By combining the A-star algorithm with APF to improve the path planning and navigation capabilities of mobile robots.

Using the A-star algorithm to plan a path for robot goal acts as a manner to improve APF. The method bases n division of the environment into a grid and applying the A-star algorithm to each grid cell to determine the optimal path [1]. Dynamic A-star is a variant of using the A-star algorithm called dynamic A-star. The dynamic A-star algorithm can adapt to changes in the environment and avoid getting trapped in local minima [2].

Other studies have proposed modifications to the A-star algorithm to incorporate the APF, whose field acts as a cost function through the modified A-star algorithm. The modified algorithm calculates the cost of each potential field cell and uses it as a distance metric in the A-star algorithm [3]. Another modified A-star algorithm is to use the potential field as an additional heuristic function. This heuristic function considers the distance between current cell and its goal and its potential value cell [4].

The traditional APF method belongs to a path planning algorithm for robot classically, and it plans the robot's path by computer algorithms that treat the robot and the obstacle as a model of the interaction of charged particles and charges. However, the algorithm has some problems, such as easily falling into local optimal solutions, requiring manual adjustment of parameters, and high complexity of the algorithm. These problems limit the effectiveness about how the traditional APF works on practical applications. For example, in the fields of self-driving cars and UAVs, the APF has difficulty in adapting to the complex environmental changes and requirements on path planning in real time [5,6].

One improvement to APF is the Augmented Artificial Potential Field (AAPF) method, which adds a rejection field to the traditional APF method to better handle complex environments and avoid local minima traps [7]. Another improvement is the Adaptive Artificial Potential Field (AdAPF) method, where AdAPF adjusts the potential field parameters according to the environment and robot configuration, which can improve the adaptability of the method [8].

Recently, deep learning-based methods have also been proposed to improve APF methods. This approach is based on the reinforcement learning APF method, which allows learning the optimal parameters of the potential field through iterative trials [9]. Another APF method based on deep neural networks is proposed to better handle complex environments and reduce local minima traps [10].

In conclusion, the APF method has limitations in dealing with complex environments, and researchers have proposed modifications to overcome these limitations. Incorporating the A-star algorithm into the APF method is one such modification that can improve the path planning and navigation capabilities of mobile robots. The details of the proposed modifications and their advantages over the original APF approach are discussed in the following sections.

2. Method

1.1. Traditional artificial potential field method

Traditional APF method bases on an algorithm with physical path planning and takes the location place of robot as potential field, thus applying force with gravitation and repulse, facilitating robot to move through the gradient direction of potential field through the gradient descent method to reach the end point finally. In the traditional APF method, robot location environment can be divided into two parts: free space and obstacles. There are no obstacles in the free space, and the robot can move freely in it. Obstacles, on the other hand, robot with forces of exert repulse helps prevent obstacles. When robot arrives at the point of target, the force with gravitation will exert the robot and decrease to zero and the robot stops moving.

In the traditional APF method, representation of robot location environment could have two dimensions or three-dimensional field, and the potential energy at each point can be expressed as

\( U(x,y)={U_{att(x,y)}}+{U_{rep(x,y)}} \) (1)

where \( {U_{att(x,y)}} \) indicates energy for gravitational force potentially and \( {U_{rep(x,y)}} \) denotes the force with repulse potentially, thus the potential energy of gravitational and repulsive forces can be expressed as

\( {U_{att(x,y)}}=\frac{1}{2}*{k_{att}}*{d^{2}} \) (2)

\( {U_{rep(x,y)}}=\frac{1}{2}*{k_{rep}}*{(\frac{1}{d}-\frac{1}{r})^{2}} \) (3)

where d denotes how long it is from robot to target point, and r indicates robot radius, while \( {k_{att}} \) and \( {k_{rep}} \) denote the constants of forces with gravitation and repulse. Within APF method, robot position attribute to forces with gravitation and repulse, and robot velocity is

\( V=-grad(U(x,y)) \) (4)

where grad denotes the gradient operator and \( U(x,y) \) denotes the robot location energy potential. The robot moves along the gradient direction until it reaches the target point.

The advantage of the traditional APF method lies in understanding and implementing easily. However, it also has some problems like being too easy to have path planning with low efficiency and accuracy without optimal local solutions. Thus, the author intends to find a method which could improve the utilization of traditional APF method with the introduction of the A-star algorithm to improve the efficiency and accuracy of path planning.

1.2. A-star algorithm

The A-star algorithm belongs to common path planning which could find the optimal one throughout the point by heuristic search. a cost function \( f(n) \) is used to measure the "goodness" of a node n. The cost function can be expressed as

\( f(n)=g(n)+h(n) \) (5)

where \( g(n) \) shows costs throughout the process in real sense from node n and \( h(n) \) denotes the estimated cost from node n to the end point. the A-star algorithm maintains both the open and closed list in the process. At the beginning, only the starting point is in the open list. In the open list, each time when node n with \( f(n) \) is selected, it will remove from it accordingly thus adding to the closed one. For the node n successor, when node is not in the closed list, calculate its cost function \( f(n) \) , if node n is absent in the open one, it will be added to the open list, otherwise compare the new cost with the old cost, and if the new cost is smaller, update the cost function and the parent node until finding emptiness in end point or open list.

The advantage of the A-star algorithm lies in guaranteeing the optimal solution, and to some extent, it can avoid problems related to optimal solution in local position. While A-star algorithm has the drawback, that is, the cost function needs to be evaluated for each node, which leads to low search efficiency.

1.3. Problems with the traditional artificial potential field method

The traditional APF method belongs to the algorithm for robot path planning with basis of environmental information perceived by the robot and guides the robot's movement by calculating the potential gradient at the robot's location. However, it also has the following problems:

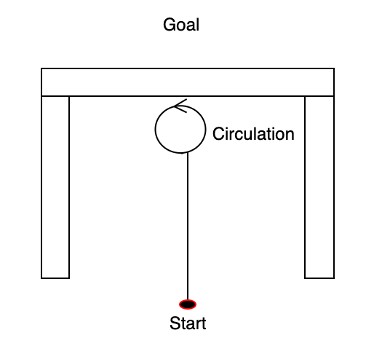
(1) Local minima problem

As shown in figure1 (a) below, the robot fails to reach the target point due to the local minima caused by the gravitational and repulsive forces. This is shown in figure1 (b) below. In this example, starting from the starting point, the robot cannot reach the end point because it is surrounded by a wall and the potential minima occur in incorrect locations, causing it to make circular oscillatory movements in front of the obstacle, thus preventing it from reaching the end point.

Figure 1. Problems. (a) Stationary after falling into local minima; (b) Oscillation after falling into local minima.

(2) Path dependence problem

The traditional APF approach attributed to path planning effects, as the robot starts at the starting point and first avoids the obstacles to be pulled to the end, but due to the potential gradient points at the robot's location in the opposite direction of the planned path, the robot will go around to the end.

(3) Dynamic obstacle problem

APF does not handle dynamic obstacles well, as from the starting point, the robot starts to avoid the obstacle, but as the obstacle moves, the robot is unable to adjust its path in time, resulting in collisions with the obstacle.

These problems make it difficult to apply it to real-world robot path planning problems. To overcome these problems, researchers have proposed many improved artificial potential field methods, such as the method with elastic band potential field and virtual obstacle and hierarchical artificial potential field. Below, the author will solve the issue of traditional APF through the introduction of A-star algorithm.

1.4. Improved method

For improving traditional APF method, A-star algorithm is introduced, and another method is made for further improvement. Specifically, the method avoids the problem of local optimal solutions by evaluating the cost function for each node in the robot path planning. Specification for the method is:

(1) First, the potential field of robot location environment produces through traditional APF method.

(2) Then, with potential field, the optimal path throughout the whole process is gained through the A-star algorithm.

(3) Then, by taking position of the robot as initiative point, and optimal path node as ending point, the potential field is generated again using the method, thus gaining the best path from the robot's position to the next node is generated using the A-star algorithm.

(4) Move the robot along the paths generated in the second and third steps.

(5) Repeat steps three and four until the robot reaches the end point.

Combining the A-star algorithm and APF method, \( f(x)=g(x)+U(x) \) , where \( g(x) \) shows the costs from initiative to the point x and \( U(x) \) expresses energy potential for the point x. The function \( U(x) \) and its energy potential is

\( U(x)=k*{U_{att(x)}}+{U_{rep(x)}} \) (6)

where \( {U_{att(x)}} \) is the attraction function that represents the potential energy from point x to the end point is

\( {U_{att(x)}}= λ*d(x,goal) \) (7)

where \( d(x,goal) \) shows how far from point x to the end, and \( λ \) acts as adjustment that controls the magnitude of the attraction.

\( {U_{rep(x)}} \) is a repulsive function that represents the potential energy from point x to the obstacle and can be expressed as

\( {U_{rep(x)}}=\sum ({1/d(x,obstacle)^{m}}) \) (8)

where obstacle denotes an obstacle, \( d(x,obstacle) \) shows how far it is from point x to the obstacle, and m acts as an adjustment which controls force repulse magnitude.

To a certain degree, the advantage of this method is that it can avoid the problem of local optimal solutions, thus improving the search efficiency and the path planning accuracy. Specifically, the use of the A-star algorithm can ensure path optimalization, and traditional APF could avoid obstacles and generate potential fields quickly and effectively. The combination of the two can improve the path planning accuracy while ensuring the efficiency.

2. Result

For verifying how does the improved APF method work and affect, experiments are conducted in this paper. The experiments are implemented using MATLAB, and the environment in which the robot moves is a 10*10 grid world, in which obstacles occupy part of the grid. The robot starts at (0,0) and ends at (10,10). within traditional and the improved APF methods, \( {k_{att}} \) sets at 35 and \( {k_{rep}} \) sets at 10.

Results are in the figure 2. Among them, the blue path indicates the path and black path generated by the traditional APF method and the improved one respectively. While the black path is more direct, avoids the problem of local optimal solutions, and has higher path planning accuracy.

Figure 2. Results. (a) Traditional APF path planning; (b) Improved method obstacle avoidance path.

3. Conclusion

The research has a proposal of using an improved method to improve path planning by introducing the A-star algorithm into the traditional artificial potential field method. Through experimental verification, the method avoids local optimal solutions to a certain extent and can improve the path planning accuracy and efficiency. Therefore, this method is feasible to robot path planning.

It is worth noting that the improved method in the research is just an idea of individual, and the specific implementation method and parameter settings need to be adjusted according to the specific problem. In addition, the experiments in this paper are only for smaller grid worlds, and for more complex environments, further research and methods to introduce other excellent path planning algorithms into the APF method in traditional sense are needed to further improve the path planning with efficiency and accuracy.