1. Introduction

With the development of artificial intelligence and intelligent robots, the delivery of robots in various fields, especially in the medical field, becomes more and more common, and more and more robots are used for such work.[1]. In such a work, robots usually only need to send back and forth between two fixed positions, but due to the particularity of their workplace, there may be many random obstacles to prevent the robot from being established. At this time, a qualified obstacle avoidance program is very important [2].

Therefore, in this paper, will aim to show an algorithm that can deal with this situation. In addition, this paper will also discuss the differences in the efficiency of different algorithms in automatic pathfinding and route planning.

This paper mainly uses Matlab as the main development tool. This paper can be used as an algorithm reference and example for automated delivery robots, as well as a reference for the efficiency of the A-star algorithm and the Dijkstra algorithm in different scenarios.

2. Related work

2.1. Introduction to related algorithms

\( f(n) = g(n)+h(n) \) (1)

The A-star algorithm combines the characteristics of the best priority algorithm and the Dijkstra algorithm, and calculates the optimal path based on the A-star function. Among them, the heuristic algorithm plays an important role. To put it simply, the heuristic algorithm determines the form of the A-star algorithm. For example, when the result of the heuristic function is 0, the A-star algorithm will be transformed into the Dijkstra algorithm. This feature will also be used in the following research [3].

2.2. Algorithm comparison

Dijkstra's algorithm focuses on the distance from the starting point to all other points, while the A-star algorithm is dedicated to finding the shortest path between two points. Therefore, in the scenario discussed in this paper, the A-line algorithm is theoretically more suitable as the basic mathematical model for building programs [4].

2.3. Procedurally generated

The pathfinding program contains two files, main and A-starA-star, run the main program to run the main program.

The A-starA-star file is mainly used to implement the A-starA-star algorithm. First of all, specific map parameters and obstacle parameters, such as the starting point of the robot or the location of obstacles, will be input into the algorithm to simulate the detector of the robot. Then you can start the A-star algorithm part. First, initialize the variable and add the starting point to the closelist, and then search for the path in a loop. During the search, the attributes of the child nodes will be calculated, such as whether the node is outside the map or an obstacle, and then the algorithm will calculate the cost of each node according to the function. And judge whether the node is in the openlist, if so, judge whether the cost of the new node is higher, otherwise, directly add the node to the openlist, until the end point is also added to the openlist, it proves that the shortest path has been found. If the open list is empty, it proves that the program cannot find the path. In the process of traversing nodes, the calculated cost will be used as the main parameter to generate the shortest path and the points of the shortest path will be added to the open list, and the close list will be traversed but inappropriate points [5].

Figure 1. Generated map.

According to figure 1, after the program has run, the generated map and the calculated path will be displayed in the form of figure 1. The dot in the red circle in the figure represents the starting point, the dot in the blue circle represents the end point, the red line represents the route planned by the program, black represents impassable obstacles and white is passable area. In this example picture, the program generates three obstacles, namely two rectangular obstacles and one circular obstacle. Among them, the rectangular obstacle and the circular obstacle block the running path of the delivery robot, so the program avoids them and finds the shortest path from the start point to the end point.

In the main program, it is mainly responsible for the realization and display of the entire program. At the beginning of the program, all existing windows will be cleared first, and then a fixed-size map (400*400) will be generated and obstacles of random positions and sizes will be generated on the map. Next, use the Euclidean heuristic function to search for the cost of each point, check points around and add the point to the openlist. If a better point is found, add the point of the openlist to the closelist until the end point is added to the open list. A path generated based on the A-star algorithm will be obtained.

After the program finds the shortest path, the program will calculate the time statistics of the shortest path and the proportion of the generated obstacle area in the map as the next research data, and display the calculated path in the form of a drawing.

2.4. 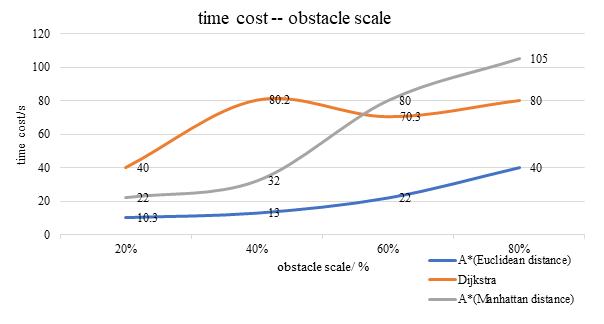Comparison of the results of the two algorithms

Figure 2. Experimental data (time cost against obstacle scale).

According to Figure 2, the orange curve represents the performance of Dijkstra's algorithm in the program, and the blue curve represents the performance of the A-star algorithm using the Euclidean heuristic. In general, the A-star algorithm takes less time than the Dijkstra algorithm in terms of time consumption regardless of the size of the obstacle in the map. In more detail, as obstacles occupy a larger area in the map, both algorithms spend more time computing the shortest path. However, the A-star algorithm takes more and more time as the obstacle area increases, while the Dijkstra algorithm takes a stable time between 70 and 80 seconds when the obstacle area becomes larger.

After the program was successfully built and 100 trials were performed, we obtained a set of data describing the efficiency of the A-star algorithm and the Dijkstra algorithm in a fixed-size map to deal with random obstacle scenarios to complete the delivery task. The data contains the best path obtained by the program time, which is used to describe the time consumption of different algorithms to obtain the results. And the proportion of the area of the obstacle randomly generated by the program in the overall map area, which is used to describe the degree of congestion of the map. A larger obstacle means that the obstacle is more likely to block the robot's running route, and the robot has a greater possibility of needing to avoid obstacles. The efficiency ratio of the final two algorithms is obtained through the complexity of time (the larger the efficiency, the more efficient it is to spend less time to complete a more crowded map).

As can be seen from the table 1, as roadblocks gradually occupy more space on the map, the robot has to do more evasion to bypass them, so the robots supported by different algorithms spend more time overall. When the map size and random obstacles are fixed, A-star algorithm is more advantageous than the Dijkstra algorithm in completing point-to-point tasks.

Table 1. Points traversed by A-star algorithm and Dijkstra algorithm in finding the path.

Continue to analyze the reasons through our previous progrom, after comparison, it is found that when the two algorithms are looking for the optimal path in the same map, the Dijkstra algorithm often needs to traverse the entire map to find the optimal path. Therefore, compared with the A-star algorithm, the Dijkstra algorithm has data in its close list that is much larger than the A-star algorithm, which makes the Dijkstra algorithm very inefficient and not suitable for use in hospitals [6] [7].

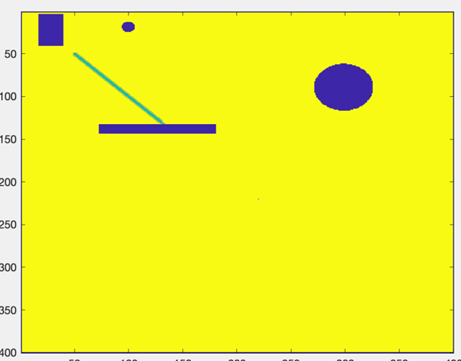
Figure 3. A-star algorithm.

Figure 4. Dijkstra algorithm.

As can be seen from the figure 3 and figure 4, these two graphs are screenshots from the points traversed in real time while the program is running to find a feasible path. According to figure3, it represents how the A-star algorithm finds the optimal path. When the program is running, it will automatically calculate the lowest cost point around the starting point, until the running path is blocked by obstacles, the path will go back to the starting point and repeat this process [8]. The process until the optimal path is found (reaching the point to bypass the obstacle), so it appears as a thick straight line on the way, which is actually composed of many straight lines composed of single points.

According to Figure 4, this figure shows the logic of the Dijkstra algorithm when traversing the path, traversing all points from the starting point as the origin to the outward circular radiation [9]. So its image is circular.

Further, use a more concrete way to show the operation logic of different algorithms. When the A-star algorithm finds the path, it tends to find the path in a straight line (similar to the best first algorithm), while the Dijkstra algorithm is more accurate when traversing the surrounding points. Like a flood, all the surrounding points will be traversed from the starting point to the starting point. This is mainly because of the heuristic algorithm, which makes the A-star algorithm tend to explore towards the end point when calculating the path, so that the amount of data that the program needs to process is greatly reduced [10].

3. Conclusion

The conclusion is that the automatic pathfinding program written in this paper can be well applied in a fixed map with randomly generated and randomly sized obstacles, and the simulated robot can go from the starting point, bypass the obstacles and reach the end point very well. In addition, the A-star algorithm in this scenario is more efficient than the Dijkstra algorithm, because the A-star algorithm does not need to traverse all the points to obtain the optimal path in the process of obtaining the shortest path, while the Dijkstra algorithm will traversing all the points makes Dijkstra's algorithm take more time.

First of all, in terms of programming, the proportion of the size of the obstacles generated by the program in the map may not fully describe the degree of congestion of a map, which may lead to inaccurate final results. In addition, too few statistical data samples may also lead to a large deviation in the final result, because the obstacles generated by the program cannot be guaranteed to be on the running path of the robot, which may lead to the calculation of the shortest path. There is a big difference in time. (Especially the automatic pathfinding program under the A-star algorithm.)

In the future, the map may be set larger and more obstacles may be added, and the space complexity may be used to describe the degree of congestion of the map. And, in the future, this program will continue to work on the development of obstacles that can automatically avoid movable random sizes and generate random positions, so as to be more suitable for the working environment of the robot in the hospital environment.