1. Introduction

With the increase of electronic-commerce business, Internet users receive a huge number of emails every day, which are mixed with a bountiful number of advertisements. Some emails contain pornographic, violent, and even virus mails, all of which are called spams [1]. A huge problem for distinguishing spams and normal emails is that almost all spams contain fake electronic email accounts and personal information, which are also included in normal emails [2]. Spam text messages involve pornographic service advertisements, fake certificate production, economic fraud, drug trafficking, etc. The interference to people’s lives has reached a degree that cannot be ignored and has caused economic property losses to some users [3]. At present, the email recognition technology used at home and abroad mainly includes IP address-based identification technology and keyword matching-based identification technology. The IP address-based recognition method mainly uses the router’s access control linked list, which is relatively simple to use and can be used at all levels. The recognition technology based on keyword matching mainly identifies the content of emails, which is often more flexible [4]. All rules-based recognition methods need to update the feature library regularly, which costs a lot of manpower. The content-based recognition has been effective, but the performance of the traditional naive Bayesian model in text classification is lagging behind the deep learning model [5]. Checking the probability of spam through machine learning is one of the most advanced technologies for identifying whether random emails are spam or regular emails. The goal of this paper is to calculate the estimated number of spams in a given range of emails by using machine learning and polynomials in order to raise public awareness. This increased recognition will decrease the possibility for people to disseminate their personal information easily, such as their bank card number and password, which will benefit the entire society by getting rid of online swindles.

2. Technical background

2.1. Definition of spams

Spam: In the absence of the recipient’s request or consent, various forms of emails with promotional content received are called spam. It mainly has the following characteristics: (1) Uninvited; (2) The content of the email contains a large amount of false information; (3) The mail is usually sent to the user’s mailbox in batches [6].

2.2. Linear regression logarithm and model

Linear regression is a machine learning algorithm. This algorithm is based on supervised learning. It performs a regression task. The regression model predicts the target value based on independent variables. This model is mainly used to identify the relationship between variables and predictions [7].When the independent variable of the regression model contains both functional and scalar mixed data and the variable only contains scalar data, Zhang et al. proposed a partial function linear regression model. The specific expression is:

\( {Y_{i}}={∝_{0}}+{∝^{ \prime }}+\int _{a}^{b}β(t){X_{I}}(t)dt+{ε_{i, i=1,2,⋯,n, }} \) (1)

Where n represents the number of functional data samples; α0 represents the intercept term; Zi = (Zi1, Zi2, ····, Ziq)′ is the q dimension scalar independent variable; α = (α1, α2, ····, αq)′ is q Dimensional regression coefficient; Xi(t) is a functional variable and squarely integrable on [0, 1]; β(t) is the regression coefficient function; εi is a random error term with zero mean and variance σ2, and it is assumed to be independent of the independent variable. a and b represent the integral interval of the upper and lower limits which can be converted to the [0, 1] range according to actual needs. For the convenience of expression, the following content is assumed to be converted to the [0, 1] interval. For the estimation of the partial function linear regression model of formula (1), first accurately represent the functional data and regression coefficient function, and then substitute the regression model for estimation. When the functional independent variable in the regression model has the characteristics of dependence, the existing function representation method based on the main component of the function will lead to inaccurate function representation because its sample covariance function is no longer a consistent estimate of the overall covariance function, which will affect the estimation effect of the regression model [8].

2.3. Logistic regression logarithm and model

Logical regression is a generalized linear regression analysis model. It often solves the secondary classification problem. Given a data set consisting of n samples \( (X, Y)=\lbrace ({x_{1}}, {y_{1}}),⋯,({x_{n}}, {y_{n}})\rbrace \) , where \( {x_{i}}={(1, x_{i}^{1}, x_{i}^{2},⋯, x_{i}^{d})^{T}} \) represents the jth feature of the sample \( {x_{i}} \) , \( i=1,2,⋯,n, j=1,2,⋯,d, \) , the first element 1 is used for the calculation of the bias term, and \( {x_{i}} \) should be labeled \( {y_{i }} ϵ \lbrace -1,1\rbrace \) .

In the logical regression algorithm, the Sigmoid function is used to construct the probability of the category to which the sample xi belongs:

\( P({y_{i}}=1|{x_{i}},ω)=\frac{1}{1+{e^{-{y_{i}}{ω^{T}}{x_{i}}}}} \) (2)

where weight vector \( ω={({ω_{0}}, {ω_{1}}, ⋯, {ω_{d}})^{T}} \) is an optimized model parameter. In logical regression, the error between the predicted value of the model and the real value is evaluated by the loss function, which is defined as:

\( L(X,Y,ω)=\frac{1}{n}\sum _{i=1}^{n}{log_{a}}{(1+{e^{-{y_{i}}{ω^{T}}{x_{i}}}})} \) (3)

The gradient descent minimization formula (1) is usually used to obtain the optimal the model parameter \( ω \) . In the \( t \) iteration, \( ω \) is updated by \( {ω_{t+1}} \) :

\( {w_{t+1}}={ω_{t}}-\frac{ η}{n}\sum _{i=1}^{n}(\frac{1}{1+{e^{{-y_{i}}{ω^{T}}{x_{i}}}}}-1){x_{i}}{y_{i}} \) (4)

where η is the learning rate. When the value between the model parameters \( {ω_{t}} \) and \( {ω_{t+1}} \) is less than the given threshold \( ε \) or reaches the maximum number of iterations, the training is terminated [9].

2.4. Spam filtering system

The filtering mode adopts online learning (Figure 1). It is centered around filters and trainers and is divided into two parts: filtering and training. The filter determines the attributes of each email based on the feature library. The trainer learns the filtering results of emails based on user feedback. It will also further adjust the corresponding features and weights in the feature weight library, with the aim of improving the adaptability and performance of the filter [10].

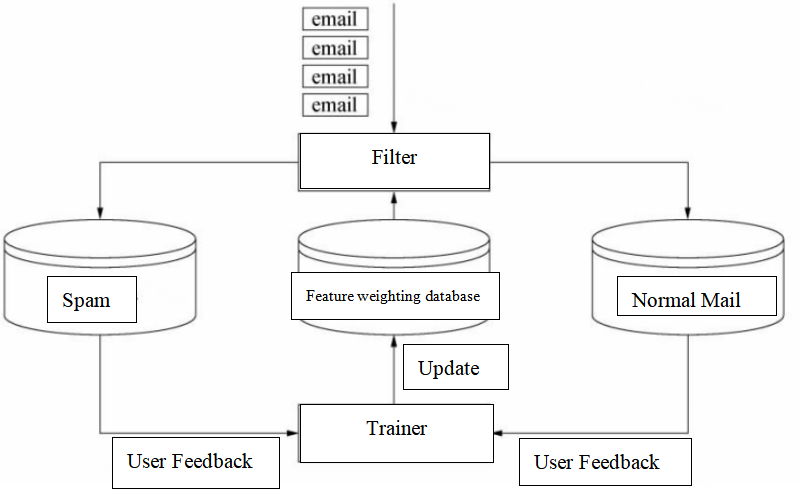
Figure 1. Spam filtering online mode [10]

3. Results and discussion

3.1. Logistic regression algorithm

3.1.1. Sorting learning strategy based on 1-AUC index. The spam filter will calculate the score for each message to predict the possibility of the message being spam. After the score of each email is known, sm% can be calculated as the function of hm% (sm% represents the misjudgment rate of spam, hm% is the ham misjudgment rate). The graphical representation of this function is a ROC curve (full rate-error rate curve). The area below the ROC curve is the cumulative measurement. This measurement is the accumulation of the effectiveness of the filter for all possible values. Because hm% and sm% measure the failure of the filter rather than the effectiveness, to be consistent, the area above the ROC curve is used as the evaluation index of the spam filter, that is, (1-AUC)% [9].

3.1.2. Experiment settings. The test data of spam filtering comes from the public evaluation data set provided by TREC(Text Retrieval Conference), CEAS (Conference on Email and Anti-Spam), and SEWM (Search Engine and Web Mining). The physical conditions of each data set are shown in Table 1. According to the above evaluation, this article uses (1-AUC)% as the evaluation index of the filter, and the logical average misjudgment rate (lam%) is also used for reference to estimate the error bound for testing emails.

Table 1. Test data set [9].

This experiment is in Ubuntu 10. 10 environment written in C language. In the special model, the section-level n-grams (n=4) feature extraction method is used to extract the characteristics of the message from the first 3,000 characters of each message and establish the feature space vector.

Through the result, it is obvious that the probability of spam’s frequency in a given range of data can almost be up to 80 percent in SEWM10, which indicates that people should strengthen the awareness of prevention more consciously than what most people think of.

Figure 2. Change of filter performance (1-AUC)% with change of m value [9].

Figure 3. Change of filter consumption time with change of m value [9]

In the online sorting logistic regression model, the algorithm is adopted to use the time series to sample the mail. Only the mail sequence pair formed by the current mail and its previous m mail is selected as the selection training sample, not all samples are selected. With the change of the m value of the selected sample number, the performance change of the filter is shown in Figure 2. From Figure 2, it can be seen that when the m value gradually increases between 2 and 10, the filter performance improves sharply. When the m value is greater than 10, the performance of the filter changes slowly; when the m value reaches 100, and after that, there is almost no change in the performance of the filter. However, it can be seen from Figure 3 that as the value of m gradually increases, the time of filter consumption also increases gradually. Therefore, with the increase of m, the filter performance is close to a stable state, but the time consumed by the filter has been increasing. For the filter system, the greater the value of non-m, the better. In the practice of this text, the parameter m used is 100 [10].

3.2. Linear regression logarithm

The variables on the x- and y-axes are the number of normal emails and the number of spams, respectively. Based on the extrapolated result, the equation of the red line is approximately y = 2.15x, which means that the number of spams is greater than the number of normal emails by a factor of 2.15, 68.3% of spams and 31.7% of normal emails, as shown in Figure 4 and Figure 5.

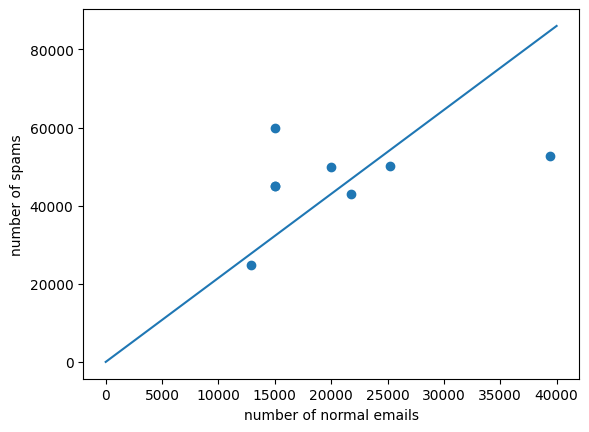
Figure 4. An estimated linear function of spams and normal emails.

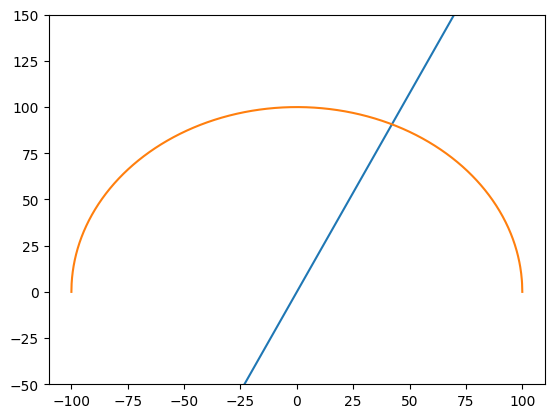
Figure 5. A Cartesian coordinate representing the probability of spams.

4. Conclusion

This paper estimates the probability of spams through machine learning. Based on the spam data from logistic regression, it is obvious that spams occupy a major part of email. Next, a contrasting diagram through logistic regression machine learning to reflect the relationship between the total number of emails and the efficiency of filtering shows that current methods of recognizing spams need improving. Finally, linear regression machine learning transforms table data and histogram data into a linear image, showing the public how widespread and uncontrollable spams is now, which strengthens the public’s vigilance against emails and prevents the elderly and minors from being deceived through spam messages. This paper mainly discusses the probability of spams in a given range of data, but there are a couple of drawbacks and limitations: (1)Spam makers will improve their skills of producing more advanced fake mails, making them more reliable to commit online fraud. (2) A huge number of current spams cannot easily be found through some basic recognition, so those reports of the proportion of spams occupied underestimated the actual proportion of spams. In the light of these two significant issues, experts in the field of examining spams are supposed to raise the level of surveillance approaches that spam makers implement to spread and make spams. Future research will use more complex models, such as polynomial regression, to receive a more accurate result than it does from linear regression and logistic regression.

Acknowledgement

First of all, I want to thank my parents for their greatest concern and support in writing this paper. Then, I want to thank all the authors of literature reviews I have learned from and thank you for giving me a great knowledge base. Without all their enlightening and impressive kindness, I could not have completed my thesis.