1. Introduction

Auctions are a fundamental mechanism for resource allocation and pricing. Auctions are used from selling goods such as art and antiques, to government procurement, and in financial transactions such as the IPO book building, where auction process is used to determine the price of a share. Understanding bidding behavior and expected revenue for bidders and auctioneers is crucial to help them to decide which types of auctions would best suit the product they are trying to buy or sell and design fair and effective mechanisms.

This study mainly focuses on the four types of seal-bid auctions: First-Price, Second-Price, Third Price, and All-Pay Auction, and discusses the equilibrium strategies and the auctioneer’s expected revenue in each of the four types of auctions and compare them among each other. What is the equilibrium biding strategies under each auction format? How does the expected revenue compare in different auction formats?

If assuming that for each type of auction, there exists an equilibrium strategy b(v), where v is the true value for the bidder, it is then possible to construct and mathematical model for the expected value  $$ \mathrm{\pi }$$ (x) for bidders. Since b(v) is the best strategy and everyone uses it, one could calculate the maximum point of  $$ \mathrm{\pi }$$ (x) and thus determine the bid function itself. Using the bid function, calculate the expected revenue from the sum of probability of winning multiplied by the profit made after winning. From this and comparing them with different types of auctions, maybe there is a pattern of expected revenue in different types of auctions.

2. Types of auctions

Sealed bid auctions are auction formats where each bidder submits a bid without knowing others’ bids. The allocation of the price will depend on the rules of specific types of auctions. In a first-price auction, each bidder submits their bid, and the price will be allocated to whoever submitted the highest value. The winner must pay whatever they submitted to the auctioneer. In a second-price auction, the process is repeated; however, the highest bidder must pay the second-highest price submitted by other bidders in the auction to the auctioneer. Similarly, in a third price auction, the highest bidder pays the third-highest price submitted if they won the price. All pay auctions are slightly different from the three above; the rule is the highest bidder still wins the auction, but all bidders, including the winner in the auction, must pay their submitted value even if they did not win the price.

3. Equilibrium bidding strategies

To construct a mathematical model simulating the behavior of bidders during an auction, first assume all bidders are rational, meaning that they will all want to maximize their profit, and there exists a symmetrical equilibrium strategy. In game theory, symmetric games mean the payoffs of players are the same no matter who is playing what strategy [1]. This means there is a unique Nash equilibrium for the game; there is a strategy that maximizes players’ utility function [2]. For example, all bidders are identical on the day before the auction; on the day of the auction, all bidders who are going to participate in the auction wake up with a true value; only the bidder knows their own true value; and all bidders will use the same strategy: if the bidder’s value is v, then bid b(v).

3.1. First price

Since there is a symmetric equilibrium strategy for each type of auction let the bid function b(v) be,

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{k}\mathrm{v}$$

where k is a constant and v is the true value.

The expected value  $$ \mathrm{\pi }$$ (x) of the bidder will be

$$ \mathrm{\pi }\left(\mathrm{x}\right)=\mathrm{P}\mathrm{r}\left(\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)\times (\mathrm{v}-\mathrm{x})$$

Next step is to calculate the probability of winning the auction when bidding the value x. First, draw a graph of the bid function. The x-axis represents the bidder’s true value, and the y-axis represents the value that the bidder should submit according to the symmetric equilibrium strategy. It is linear because the assumption is that the bid function is some constant times v and it must be below the 45°-line because if the bid value is higher than the bidder’s true value, then they would make a negative profit; hence, any function above the 45°-line in a first-price auction cannot be the equilibrium strategy even if there exists one. If a bidder bids value x and wins the auction, this means that all true values of other bidders must be below  $$ \frac{\mathrm{x}}{\mathrm{k}}$$ . There are n people participating in the auction. Excluding the winner, there are n-1 participants. The probability of one person that is below  $$ \frac{\mathrm{x}}{\mathrm{k}}$$  is  $$ {\mathrm{ }\left(\frac{\mathrm{x}}{\mathrm{k}}\right)}^1\mathrm{ }$$ , the probability of two people that is below  $$ \frac{\mathrm{x}}{\mathrm{k}}$$  is $$ {\mathrm{ }\left(\frac{\mathrm{x}}{\mathrm{k}}\right)}^2$$ , so the probability of everyone else that is below  $$ \frac{\mathrm{x}}{\mathrm{k}}$$  is  $$ {\mathrm{ }\left(\frac{\mathrm{x}}{\mathrm{k}}\right)}^{\mathrm{n}-1}$$ . Hence, the probability of winning the auction when bidding the value x is  $$ {\mathrm{ }\left(\frac{\mathrm{x}}{\mathrm{k}}\right)}^{\mathrm{n}-1}$$  (Figure 1).

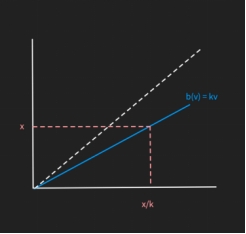
Moving back to the expected value function  $$ \mathrm{\pi }$$ (x) as we now know the probability of winning when bidding x,

$\pi (x)=(\frac{x}{k}{)}^{n-1}(v-x)\mathrm{.}$

Since b(v) is the symmetric equilibrium strategy, at point x, which is also kv,  $$ \mathrm{\pi }$$ (x) must be at its maximum point. Therefore,

$\pi \mathrm{\prime }(kv),=0.$

Using the two equations above, solve k in terms of n, which is the number of participants in the auction to get a bid function for first price auction.

Expanding brackets,

$$ \mathrm{\pi }\left(\mathrm{x}\right)=\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right)\left(\mathrm{v}\right){\left(\mathrm{x}\right)}^{\mathrm{n}-1}-\mathrm{ }\frac{{\mathrm{x}}^{\mathrm{n}}}{{\mathrm{k}}^{\mathrm{n}-1}}$$

Differentiating  $$ \mathrm{\pi }$$ (x),

$$ {\mathrm{\pi }}^{\mathrm{\text{'}}}\left(\mathrm{x}\right)=\left(\mathrm{n}-1\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right)\left(\mathrm{v}\right){\left(\mathrm{x}\right)}^{\mathrm{n}-2}-\left(\mathrm{n}\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{x}\right)}^{\mathrm{n}-1}$$

Compute  $$ \mathrm{\pi }\mathrm{\text{'}}$$ (kv) = 0 and simplify,

$$ {\mathrm{\pi }}^{\mathrm{\text{'}}}\left(\mathrm{k}\mathrm{v}\right)=\left(\mathrm{n}-1\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right)\left(\mathrm{v}\right){\left(\mathrm{k}\mathrm{v}\right)}^{\mathrm{n}-2}-\left(\mathrm{n}\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{k}\mathrm{v}\right)}^{\mathrm{n}-1}$$

$$ \left(\mathrm{n}-1\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right)\left(\mathrm{v}\right){\left(\mathrm{k}\mathrm{v}\right)}^{\mathrm{n}-2}-\left(\mathrm{n}\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{k}\mathrm{v}\right)}^{\mathrm{n}-1}=0$$

$$ \left(\mathrm{n}-1\right)\left(\frac{{\mathrm{k}}^{\mathrm{n}-2}}{{\mathrm{k}}^{\mathrm{n}-1}}\right)=\left(\mathrm{n}\right)$$

$$ (\mathrm{n}-1)(\left(\frac{1}{\mathrm{k}}\right)=\mathrm{n}$$

$$ \mathrm{k}=\left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)$$

Finally, substituting k back into the bid function b(v), the symmetric equilibrium strategy for first price auction is

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{ }\left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)\mathrm{v}$$(1)

where n is the number of participants and v is the true value [3].

3.2. Second price

For second-price sealed-bid auctions, the equilibrium strategy will be different because the rules are different compared to first-price auctions. However, we do not need to calculate such a bid function for a second-price auction because there is a dominant strategy, where everyone who is rational will use this strategy. It is a dominant strategy in a second-price auction for a bidder to bid their true value [4]. Suppose the true value is v, and the bidder bids below v; it will not bring any benefit to the bidder because if the second-highest price of the auction is still below the submitted value, the bidder pays the same amount. Yet, bidding lower than v lowers the probability of winning, as there is a chance that someone else bids above the submitted value but lower than v. If the bidder bids above v, it increases the probability of winning, but there is also a chance that the second-highest price is below the submitted value but above v, resulting in negative profit for the bidder. Therefore, the dominant strategy for a second-price auction is to bid truthfully [5].

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{v}$$

3.3. Third price

The bid function for the third-price auction is rather different from the two types above; in the third-price auction, the winner pays the third-highest bid submitted. In this case, maybe bidders should bid over their true value to a certain extent. To calculate the bid function, do the same thing as the first-price auction; first suppose the bid function b(v) is some sort of linear equation,

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{k}\mathrm{v}$$(2)

But this time, the bid function is expected to be above the 45° line because the equilibrium strategy might expect to bid higher than the true value (Figure 2).

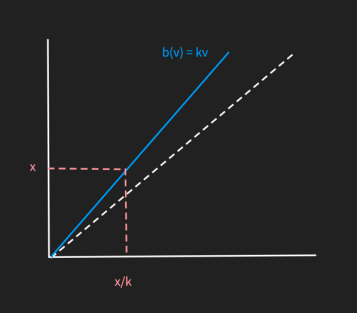
Now, compute  $$ \mathrm{\pi }$$ (x), but this time replace the submitted bid by the third highest bid like so,

$$ \mathrm{\pi }\left(\mathrm{x}\right)=\mathrm{Pr}\left(\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)\times (\mathrm{v}-\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{r}\mathrm{d}\mathrm{ }\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{ }\mathrm{b}\mathrm{i}\mathrm{d})$$

To calculate the probability of winning, it is exactly the same as the first-price auction, because both auctions allocate the price to the highest bid submitted, but the only difference is the paid amount. Since all of the values are assumed to be distributed evenly across from [0,1], the third highest bid can be written as

$\frac{n-2}{n}X$

where n is the number of participants and x is the submitted value.

The resulting two equations are as follows,

$$ \mathrm{\pi }\left(\mathrm{x}\right)={\mathrm{ }\left(\frac{\mathrm{x}}{\mathrm{k}}\right)}^{\mathrm{n}-1}\mathrm{ }(\mathrm{v}-\frac{\mathrm{n}-2}{\mathrm{n}}\mathrm{x})$$

$$$ \mathrm{\pi }\mathrm{\text{'}}\left(\mathrm{k}\mathrm{v}\right),\mathrm{ }=0$$$

Repeating the steps from first price auction, by first multiplying out the brackets,

$$ \mathrm{\pi }\left(\mathrm{x}\right)=\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right)\left(\mathrm{v}\right){\left(\mathrm{x}\right)}^{\mathrm{n}-1}-\mathrm{ }\frac{(\mathrm{n}-2){\mathrm{x}}^{\mathrm{n}}}{{\mathrm{n}\mathrm{k}}^{\mathrm{n}-1}}$$

Differentiating  $$ \mathrm{\pi }\left(\mathrm{x}\right)$$ ,

$$ {\mathrm{\pi }}^{\mathrm{\text{'}}}\left(\mathrm{x}\right)=\left(\mathrm{n}-1\right)\left(\mathrm{v}\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{x}\right)}^{\mathrm{n}-2}-\left(\mathrm{n}-2\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{x}\right)}^{\mathrm{n}-1}$$

Compute  $$ {\mathrm{\pi }}^{\mathrm{\text{'}}}\left(\mathrm{k}\mathrm{v}\right)$$  and simplify,

$$ {\mathrm{\pi }}^{\mathrm{\text{'}}}\left(\mathrm{k}\mathrm{v}\right)=\left(\mathrm{n}-1\right)\left(\mathrm{v}\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{k}\mathrm{v}\right)}^{\mathrm{n}-2}-\left(\mathrm{n}-2\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{k}\mathrm{v}\right)}^{\mathrm{n}-1}$$

$$ \left(\mathrm{n}-1\right)\left(\mathrm{v}\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{k}\mathrm{v}\right)}^{\mathrm{n}-2}-\left(\mathrm{n}-2\right)\left(\frac{1}{{\mathrm{k}}^{\mathrm{n}-1}}\right){\left(\mathrm{k}\mathrm{v}\right)}^{\mathrm{n}-1}=0$$

$$ \left(\frac{1}{\mathrm{k}}\right)\left(\mathrm{n}-1\right){\left(\mathrm{v}\right)}^{\mathrm{n}-1}=(\mathrm{n}-2){\left(\mathrm{v}\right)}^{\mathrm{n}-1}$$

$$ \left(\mathrm{n}-1\right)\left(\frac{1}{\mathrm{k}}\right)=(\mathrm{n}-2)$$

$$ \mathrm{k}=\left(\frac{\mathrm{n}-1}{\mathrm{n}-2}\right)$$

Bid function b(v) of third price auction is

$$ \mathrm{b}\left(\mathrm{v}\right)=\left(\frac{\mathrm{n}-1}{\mathrm{n}-2}\right)\mathrm{v}$$(3)

where n is the number of participants in the auction and v is the true value.

From the calculated bid function, it is shown that the equilibrium strategy for a third-price auction is to bid above the true value.

As seen from the bid function for the first price, second price, and third price auctions, there might be a pattern for those functions,

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{ }\left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)\mathrm{v}$$

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{ }\left(\frac{\mathrm{n}-1}{\mathrm{n}-1}\right)\mathrm{v}$$

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{ }\left(\frac{\mathrm{n}-1}{\mathrm{n}-2}\right)\mathrm{v}$$

perhaps the bid function of fourth price auction might be

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{ }\left(\frac{\mathrm{n}-1}{\mathrm{n}-3}\right)\mathrm{v}$$

but this can only be confirmed by proving it using similar calculations as the other auctions.

3.4. All-pay

It was very lucky that the “guess” of the bid function for the auctions above were all correct; they were all linear bid functions, with a constant k in front of the true value v. Unfortunately, the bid function for all-pay auctions is non-linear; maybe there is another “guess” of the bid function. A linear bid function for an all-pay auction does not exist because if the method above is repeated with a linear bid function, kv, the final function is not linear. This contradicts the “guess” that the bid function is linear, so the result must be invalid.

Perhaps, the bid function could be exponential, and maybe is in the form,

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{k}{\mathrm{v}}^{\mathrm{n}}$$ .

The expected value function  $$ \mathrm{\pi }$$ (x) will be slightly different compared to others because in this case, all bidders must pay their submitted value even if they did not win. Therefore, the function is now written like so,

$$ \mathrm{\pi }\left(\mathrm{x}\right)=\mathrm{Pr}\left(\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{ }\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{ }\mathrm{b}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{ }\mathrm{x}\mathrm{ }\right)\mathrm{v}-\mathrm{x}$$

where v is the true value and x is the submitted value. It must always be minus x at the end because bidders must all pay as long as they are participating in the auction.

Since the bid function is no longer the same, and it is non-linear, the probability of winning will be different; when bidding the value x, the corresponding true value, according to the new bid function, is ( $$ {\frac{\mathrm{x}}{\mathrm{k}})}^{\begin{array}{c}1\\ n\end{array}}$$ . The probability of everyone else’s true value being below  $$ ({\frac{\mathrm{x}}{\mathrm{k}})}^{\frac{1}{\mathrm{n}}}\mathrm{ }$$ will be  $$ ({\frac{\mathrm{x}}{\mathrm{k}})}^{\frac{\mathrm{n}-1}{\mathrm{n}}}\mathrm{ }$$ due to the same reasons for the calculations from the first-price and third-price auctions (Figure 3).

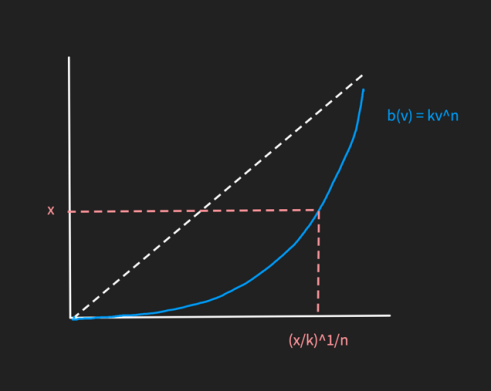
Substituting this back into  $$ \mathrm{\pi }$$ (x),

$$ \mathrm{\pi }\left(\mathrm{x}\right)=\mathrm{ }({\frac{\mathrm{x}}{\mathrm{k}})}^{\frac{\mathrm{n}-1}{\mathrm{n}}}\mathrm{ }\mathrm{v}-\mathrm{x}$$

Differentiating  $$ \mathrm{\pi }$$ (x),

$$ {\mathrm{\pi }}^{\mathrm{\text{'}}}\left(\mathrm{x}\right)=\left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)\left(\frac{1}{{\mathrm{k}}^{\frac{\mathrm{n}-1}{\mathrm{n}}}}\right)\left(\mathrm{v}\right){\left(\mathrm{x}\right)}^{\frac{-1}{\mathrm{n}}}-1$$

Computing  $$ \mathrm{\pi }$$ ( $$ \mathrm{k}{\mathrm{v}}^{\mathrm{n}}$$ ) = 0,

$$ \left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)\left(\frac{1}{{\mathrm{k}}^{\frac{\mathrm{n}-1}{\mathrm{n}}}}\right)\left(\mathrm{v}\right){\left(\mathrm{k}{\mathrm{v}}^{\mathrm{n}}\right)}^{\frac{-1}{\mathrm{n}}}=1$$

$$ \left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)\left(\frac{1}{\mathrm{k}}\right)=1$$

$$ \mathrm{k}=\left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)$$

Bid function b(v) for all-pay auction is,

$$ \mathrm{b}\left(\mathrm{v}\right)=\mathrm{ }\left(\frac{\mathrm{n}-1}{\mathrm{n}}\right){\mathrm{v}}^{\mathrm{n}}$$(4)

4. Expected revenue

4.1. Calculations

So far, an equilibrium strategy for each auction format was found using the assumptions made at the beginning. The next step is to determine which auction format would bring the most revenue for the auctioneer by calculating the expected revenue.

To calculate the expected revenue for the first-price auction, first consider the case of two bidders and adopt the same assumptions used to calculate the equilibrium strategies. The values of the draws from each bidder are independent and drawn from a uniform distribution from the interval [0,100]. One way of winning is that bidder 1 has value x and bidder 2 has value less than or equal to x, another way is that bidder 2 has value x and bidder 1 has value less than or equal to x. From this, the probability that x is the highest value is

$$ \mathrm{Probability}\mathrm{ }\left(\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }2\mathrm{ }\mathrm{b}\mathrm{i}\mathrm{d}\mathrm{s}\mathrm{ }\mathrm{i}\mathrm{s}\mathrm{ }\mathrm{x}\right)=\mathrm{ }2\left(\frac{1}{100}\right)\left(\frac{\mathrm{x}}{100}\right)$$

Now, consider there are n bidders, the probability of x is the highest value would be

$$ \mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\mathrm{ }\left(\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }2\mathrm{ }\mathrm{b}\mathrm{i}\mathrm{d}\mathrm{s}\mathrm{ }\mathrm{i}\mathrm{s}\mathrm{ }\mathrm{x}\right)=\mathrm{n}\left(\frac{1}{100}\right){\left(\frac{\mathrm{x}}{100}\right)}^{\mathrm{n}-1}$$

The expected value of the highest bid would be the integral and solving it

$$ {\int }_0^{100}\mathrm{x}\mathrm{n}\left(\frac{1}{100}\right){\left(\frac{\mathrm{x}}{100}\right)}^{\mathrm{n}-1}\mathrm{ }\mathrm{d}\mathrm{x}=\mathrm{ }\left(\frac{\mathrm{n}}{\mathrm{n}+1}\right)100$$

Since each bidder bids  $$ \left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)$$  fraction of their true value, thus, the expected revenue is  $$ \left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)$$  times the expected value of the highest bid [6].

$$ \left(\frac{\mathrm{n}-1}{\mathrm{n}}\right)\mathrm{ }\left(\frac{\mathrm{n}}{\mathrm{n}+1}\right)100=\mathrm{ }\left(\frac{\mathrm{n}-1}{\mathrm{n}+1}\right)100$$(5)

For second-price auctions, recall that the price is allocated to the bidder with the highest valuation, and the winner pays the second-highest actual valuation; therefore, the expected revenue for a second-price auction is the second-highest valuation. In a first-price auction, the bidder with the highest true value wins by estimating the value of the second highest. On average, the winner will have a valuation equal to the expected highest value if N values are drawn from the distribution; therefore, the expected winning bid on average will be equal to the expected 2nd-highest valuation [7].

4.2. Revenue equivalence theorem

From the calculations above, the expected revenues for both first- and second-price sealed-bid auctions are the same; it could be that there is a rule about expected revenues for all auction formats if they obey some specific properties. According to the revenue equivalence theorem, suppose bidders have independent and identically distributed valuations and are risk neutral. Then any symmetric and increasing equilibrium of a direct revelation auction A that assigns the item to the highest bidder such that the expected payment of the bidder with value 0 is 0, yields the same expected revenue [8]. In other words, the revenue equivalence theorem states that if there are N bidders with values drawn from the same continuous value distribution, then any standard auction will lead to the same revenue and expected bidder profit as the second-price auction [9]. Furthermore, the theorem says if each bidder’s type is drawn from a distribution where its CDF (cumulative distribution function) is increasing and continuous, bidders are risk neutral, the bidder with the highest type wins, and the bidder with the lowest possible type has an expected payoff of zero, then the expected revenue for all auctions is the same [10]. Thinking back to the auction formats of first, second, third, and all-pay auctions, they all satisfy the conditions for revenue equivalence; therefore, all four auction types in this study have an expected revenue of  $$ \left(\frac{\mathrm{n}-1}{\mathrm{n}+1}\right)$$ .

5. Conclusion

The revenue equivalence theorem showed that auction formats might not matter for revenue under ideal assumptions. However, in practice, deviations from the assumptions, such as risk aversion and asymmetric information, could change the optimal choice. There are many limitations of the model in this study because of the assumptions, and these assumptions would rarely hold. For example, some bidders may be more risk averse, whereas some bidders may be more risk seeking; this changes the bid behaviors of bidders. Another example is that bidders have different beliefs about how valuations are distributed; this would affect the probability of winning differently. Emotions such as pride and rivalry can cause bidders to overbid, which is impossible to take into account when constructing a model like this.

The bid functions discovered in this study are only the most basic types of auctions; there are much more complicated cases that have not yet managed to be solved yet. For example, in an all-pay auction, there could be three prices, which are allocated to the highest, second-highest, and third-highest bidders. To compute a mathematical model for this, a three-dimensional cube would need to be used to illustrate the three prices and winners, which makes it much more complicated and difficult. All mathematical models do not predict exactly how something behaves, but we could make it close to what would happen with idealized assumptions such as, in this case, full rationality, risk neutrality, and perfect information about probability distributions.