1. Introduction

Uncertainty is intrinsic to economic life, shaping investment, pricing, and policy. Probability theory formalizes uncertainty and supports inference, prediction, and decision-making under risk. The basic argument distinguishes probability as a measure of belief or a property of the external environment, and distinguishes measurable risk from fundamental uncertainty [1,2]. Parallel literatures propose portfolio-theoretic risk–return trade-offs [3], subjective expected utility and Bayesian updating [4], and behavioral departures from expected utility [5].

Despite rich theoretical advances, practical adoption in firms and public administration often reduces to ad hoc heuristics, incomplete variance modeling, or overreliance on point forecasts. Moreover, model uncertainty— including covariate choice, functional form, and regime non-ergodicity—can dominate errors if left untreated [1,6]. This paper addresses these gaps by: (i) setting out probability basics for economic use; (ii) mapping them to risk management and market forecasting; (iii) analyzing links to consumer behavior and demand prediction; and (iv) demonstrating with stylized cases in tourism and insurance. The aim is to present a cohesive, implementable template for probability-guided decisions while indicating where model averaging, robustness, and sensitivity analyses are warranted.

2. Probability: basic concepts

2.1. Definitions and terminology

Let (Ω,F,P) be a probability space. A random variable X has probability mass p(x) (discrete) or density f(x) (continuous). The expectation and variance are:

$E[X]={\sum }_{x}xp(x)orE[X]=\int xf(x)dx,Var\text{⁡}(X)=E[(X-E[X]{)}^2]$(1)

For events A,B with P(B) > 0, Bayes’ rule updates beliefs

$$ \text{P}\text{(}\text{A}\text{∣}\text{B}\text{)=}\frac{\text{P}\text{(}\text{B}\text{∣}\text{A}\text{)}\text{P}\text{(}\text{A}\text{)}}{\text{P}\text{(}\text{B}\text{)}}$$(2)

These operators underpin economic decisions in investing, insurance pricing, forecasting, and consumer analytics [2,4].

2.2. Canonical examples

Canonical experiments (coin tosses, dice, lotteries) clarify independence, conditional probability, and rare-event reasoning. In lotteries, the cumulative odds of winning across all prize categories are summed through mutually exclusive events; in insurance, Bernoulli trial logic provides information about expected claims and solvency buffers; in demand, binomial/Poisson approximations support inventory and workforce planning [7-9].

3. Probability in economic decision-making

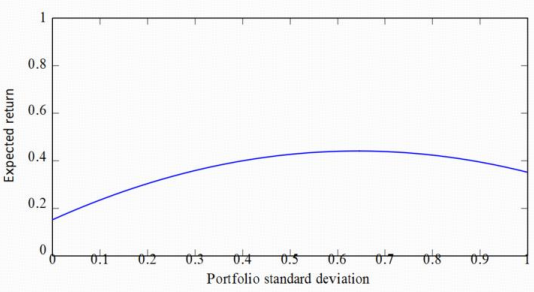
3.1. Risk management: expected value, variance, and diversification

Let a two-asset portfolio have weights w and (1−w) and (gross) returns R1,R2. The portfolio mean and variance are:

$$ \text{P}\text{(}\text{A}\text{∣}\text{B}\text{)=}\frac{\text{P}\text{(}\text{B}\text{∣}\text{A}\text{)}\text{P}\text{(}\text{A}\text{)}}{\text{P}\text{(}\text{B}\text{)}}\text{E}\text{[}{\text{R}}_{\text{p}}\text{]=}\text{wE}\text{[}{\text{R}}_{\text{1}}\text{]+(1−}\text{w}\text{)}\text{E}\text{[}{\text{R}}_{\text{2}}\text{],}\text{Var}\text{(}\text{=}{\text{w}}^{\text{2}}{\text{σ}}_{\text{1}}^{\text{2}}\text{+(1−}\text{w}{\text{)}}^{\text{2}}{\text{σ}}_{\text{2}}^{\text{2}}\text{+2}\text{w}\text{(1−}\text{w}\text{)}{\text{σ}}_{\text{12}}$$(3)

where σ12 is the covariance. Diversification operates through the covariance term, reducing variance at given ex-pected return. Efficient portfolios trace a convex frontier; capital allocation and constraints then choose operating points [3]. Distributional assumptions, estimation error, and regime shifts motivate robustness checks and model averaging [1].

3.2. Market forecasting under uncertainty

Forecasting reduces to learning P(Yt+1 | It) from historical data Dt and information set It. Probability facilitates predictive intervals, scenario probabilities, and decision-contingent expected losses. Bayesian updating is natural when covariates and specifications are uncertain; behavioral evidence warns against overconfidence in point forecasts [1, 5].

4. Probability and consumer behavior

Promotions, stockouts, and price uncertainty shape purchase timing and quantities. Probabilistic response models (e.g., logistic/probit choice) map the purchase probability to marketing stimuli and inventory states; demand distributions inform service level targets and reorder policies. Probability links subjective expectations and revealed behavior: when shocks are non-ergodic or belief-heterogeneous, aggregate responses can deviate from representative-agent predictions [2, 6].

5. Case studies

5.1. Tourism demand planning

Tourism exhibits strong seasonality and overdispersion. A simple probabilistic forecast allocates capacity (rooms, staff) to percentile demand. Suppose daily arrivals D have E[D] = µ and Var(D) = σ2. For a service-level target (e.g., 95%), set capacity C to the s-quantile qs of the predictive distribution P(D ≤ qs) = s. This balances underage and overage costs; sensitivity to µ and σ and distributional tails should be reported [10,11].

5.2. Insurance pricing and solvency

Consider n independent policyholders with claim indicator X ∼ Bernoulli(p) and claim amount L if a claim occurs. Total loss  $$ \text{S}\text{=}{\sum }_{\text{n}}^{\text{i}\text{=1}}\text{x}\text{i}$$  L has E[S] = npL and Var(S) = np(1 − p)L2. Premium π per policy is set via expected loss plus loading: π = pL(1 + λ), while capital K covers tail risk (e.g., Value-at-Risk at level α). Even with small p, aggregation risk and parameter uncertainty require buffers and stress tests [7,8]. Probability clarifies when expected-profit targets and solvency constraints are simultaneously feasible.

Notes: Values are representative of published combinatorial calculations for “6 out of 33” red plus “1 out of 16” blue formats; see expository discussions in [7].

Notes: Bernoulli-trial approximation; illustrative parameters for didactic purposes [7,8].

6. Conclusion

Probability offers a rigorous foundation for quantifying uncertainty in economic decisions, enabling explicit statements about expected outcomes, dispersion, and tail events. The analysis connects core probability operators with portfolio diversification, market forecasting, consumer response, and insurance pricing. Three messages emerge. First, expected value is crucial for resource allocation, but variance and covariance—and the resulting downside and tail risks—are crucial for resilience. Second, forecasting under model uncertainty benefits from probabilistic forecasting, scenario weighting, and Bayesian updating, particularly for decisions involving controversial covariates and parameter specifications. Third, probabilistic thinking facilitates the design of promotions, inventory policies, and insurance contracts by linking subjective beliefs to observed decision probabilities and solvency ratios. The case studies indicate how percentile capacity targets in tourism and Bernoulli-based pricing and capital in insurance can be implemented with transparent assumptions. However, practical deployment faces challenges: parameter instability, regime changes, and non-ergodicity can undermine static models; estimation error inflates.

Measured efficiency; behavioral features (loss aversion, reference dependence) distort risk-taking relative to mean–variance benchmarks. Addressing these issues calls for robust and Bayesian model averaging to account for specification uncertainty, sensitivity analyses for tail risks, and hybrid frameworks incorporating behavioral response while preserving probabilistic coherence [1,5,6]. Future work should integrate probability with causal structure learning, clarify conditions for structural stability in forecasts, and develop stress-testing templates that translate probability statements into operational early-warning thresholds for firms and policy institutions.