1. Introduction

Modern research on game theory began with Zermelo, Borel, and von Neumann. In 1928, von Neumann proved the fundamental principles of game theory, thus announcing the official birth of game theory. In 1944, the groundbreaking work "Game Theory and Economic Behavior"co authored by vonNeumann and Morgan Stanley extended the two person game to the n-person game structure and systematically applied game theory to the economic field, laying the foundation and theoretical system of this discipline. From 1950 to 1951, John Forbes Nash Jr.proved the existence of equilibrium points using the fixed point theorem, laying a solid foundation for the generalization of game theory. Nash's pioneering papers, such as "Equilibrium Points in N-Person Games"(1950) and "Non Cooperative Games"(1951), provided the concept of Nash equilibrium and the existencetheorem of equilibrium. In addition, the research of Reinhard Zelten and John Haysani also played a driving role in the development of game theory. Game theory has developed into a relatively comprehensive discipline.

The scientific nature of game theory makes it a theoretical discipline, and many developments in game theory exist in the field of mathematics. For example, the founder of game theory, von Neumann's research on game theory originated from his idea of introducing more mathematics into finance; In 1994, J.Nash from the University of California, Berkeley, was awarded the Nobel Prize for his pioneering contributions in the theory of equilibrium analysis in non cooperative games, and Reinhard Selten from the University of Bonn in Germany are also mathematician. Meanwhile, game theory is widely applied in the field of economics. There are 7 Nobel Prizes in Economics related to research in game theory.

2. Literature Review

For a best viewing experience the used font must be Times New Roman, on a Macintosh use the font named times, except on special occasions, such as program code in game theory, there is a concept of an economic person (a rational person)."Economists assume that rational individuals are expected to display consistency."[1]In this article’s hypothesis, stubborn gamblers have many additional traits compared to rational individuals. This article use additional calculations to represent these traits. Firstly, we believe that stubborn individuals have the characteristic of high communication costs, and will deduct some of the interests of both parties in the game that requires communication as a manifestation of communication costs. This definition assumes that stubborn individuals will not change their communication costs due to long-term games or external or well intention or deceptive information, nor will their stubbornness be reduced due to long-term games or emotional factors. This article distinguish stubbornness from a strong sense of vigilance or timidity, believing it to be a personal trait rather than a specific state.

Meanwhile, according to Simon's critique, when solving real-world problems, this article would assume that the rationality of the game player is limited. That is to follow the principle of maximum satisfaction rather than the principle of optimal. "The term 'bounded nationality' of characters is limited to human's information processing capabilities."[2]

Due to Maslow's critique of the hierarchy of needs theory, this article would assume that the mind needs this level. Meanwhile, according to North's book "Institutions, Institutional Change, and Economic Performance", human behavior is more complex than the content contained in the individual utility function in economist models. There are many situations where it is not just a matter of maximizing wealth, but also altruistic and self imposed constraints that fundamentally change the outcome of people's actual choices. Up to Mariano Rojas, "Development programs should not prioritize the satisfaction of a specific category of needs (i.e. physiological ones)while marginalizing the satisfaction of other needs (i.e. love and belonging ones)."[3]

Stubborn agents referred to those who were stubborn in their original opinions."; Correspondingly, if a stubborn person's strategy is changed, it will lead to certain psychological losses. By digitizing the characteristics we see in stubborn gamblers, we can clearly see why we tend to develop aversion towards them. Due to the change that stubbornness brings to the gamer, we and the stubborn gamer often cannot use the same logic to calculate our interests.

3. Methodology

The title of the classic game in this article is the most basic game can easily create the classic prisoner's dilemma, and the simplest stone scissors. Knowledge about game theory comes from recorded and published news, while knowledge about psychology comes from certified authoritative journals, famous books, and widely circulated psychological papers. This article used some academic databases to search for the data that is needed, such as Google Scholar, Springer, Science-direct, etc. After searched for content related to the discourse topic using keywords, searched for titles and abstracts, and determined their relevance to my discourse topic through manual screening, and judged their credibility as data.

After searching, this article collected 5 cited articles as supporting citations. While searching for references, I have found that there is increasing criticism, improvement, and application of the theory of rational people.I believe this is a good example of looking at problems from different perspectives, and it is also a precursor to the possibility of paying more attention to human nature in the future.

At the same time, this article applied a set of equations representing stubborn gamblers to the classic game of prisoner's dilemma, and verbally described the effects of this game, obtaining data for analysis. This approach of simulating the role of individuals with a certain trait in a game by adding additional computational complexity is also used to understand games in special situations. For example, in a publicly available game theory course posted online at Yale University, individuals who change their decisions due to emotional factors are referred to as angry angels, and it is assumed that they will deduct certain benefits if they do not cooperate in the game.

This method is called extended game theory and is a good tool for exploring psychology. To some extent it is believed that this tool can be widely applied in the future combination of psychology and mathematics, providing a basis for more logical and rigorous psychological experiments.

4. Results

4.1. Small payoff game

As shown in Table 1, this is a classic game with two Nash equilibrium. The meaning of Nash equilibrium is to achieve a balance where neither player can increase their own interests by individually changing their strategies. We set the initial point of the game to start from one of the four points randomly. A can choose up and down, while B can choose left and right. This is a game that can be communicated.

Firstly, assume that the communication cost for a stubborn person is 1, and that their initial psychological gain is 0.5, while the psychological loss if their strategy is changed is also 0.5.If both parties involved in a game are rational individuals with limited rationality, regardless of whether the game is played once or multiple times, the final outcome will always be in the optimal equilibrium in the upper left corner. However, assuming that A is a rational person and B is a stubborn gamer among these two individuals, there is only a 1/2 chance that the outcome of either one or multiple games will reach the optimal equilibrium in the upper left corner. Only by randomly moving to the two squares on the left can and must be able to achieve optimal equilibrium. If both A and B are stubborn gamblers, there is only a 1/4 chance of achieving a better equilibrium. It is worth mentioning that in the above games, the benefits of stubborn players are absolutely greater than those of rational individuals. Regardless of the outcome of the game, stubborn gamblers will have the 0.5 reward they need to satisfy in their hearts.

Assuming the same premise, the psychological gain of the stubborn person changes to 0.25, and the psychological loss of the changed strategy is 0.5.What are the changes in the current situation? When A is a rational person and B is a stubborn gamer among these two individuals, there is a three-quarters chance of achieving a better Nash equilibrium, that is, only a worse equilibrium with an initial starting point in the lower right corner may lead to the inability of both parties to reach a better equilibrium. Meanwhile, with the initial starting point on the upper right, B gains lower benefits than A. In other cases, A's returns are still strictly lower than B. Lowering the psychological gains of stubborn gamblers again will reveal that as long as the psychological gains are less than 0.5, their specific values have no impact on this outcome. When both A and B are stubborn gamblers, the result is still the same.

The game still follows this hypothetical pattern, but the player insists that the initial psychological gain chosen is 0.5, while the psychological loss of the changed strategy is 0.25.Under this premise, when A is a rational person and B is a stubborn gamer among these two individuals, the situation is exactly the same as the previous assumption, that is, there is a 3/4 chance of achieving a better Nash equilibrium, and only a worse equilibrium with an initial starting point in the lower right corner may lead to the inability of both parties to reach a better equilibrium. Meanwhile, with the initial starting point on the upper right, B gains lower benefits than A. In other cases, A's returns are still strictly lower than B. Reducing B's psychological loss will reveal that its specific value has no impact on this result.

Reduce the communication cost of the stubborn gamer to 0, and he insists on a psychological benefit of 0.5 for the initial choice, while the psychological loss if the strategy is changed is 0.5. It will be found that stubborn gamblers are unable to make changes to their initial strategy. But once either the psychological gain or psychological loss falls below 0.5, the behavior of stubborn gamblers is no different from that of rational people. At the same time, stubborn gamblers have a three-quarters chance of obtaining profits lower than rational people, and a quarter chance of being the same as rational people.

Table 1: Payoff of a game

4.2. Big payoff game

As shown in Table 2,this is a classic prisoner's dilemma game. It was in 1950 that Merrill Flood and Melvin of the Rand Corporation in the United States developed a theory related to the dilemma, which was later elaborated by consultant Albert Tucker in a prisoner's manner and named the "Prisoner's Dilemma". Two individuals who conspired to commit crimes were imprisoned and unable to communicate with each other. If neither person exposes the other, each person will be imprisoned for one year due to uncertain evidence; If one person exposes while the other remains silent, the whistle-blower shall be immediately released for meritorious service, and the silent shall be imprisoned for 20 years for non cooperation; If exposed to each other, both parties will be sentenced to 9 years in prison due to conclusive evidence. In our case, it is assumed that both parties in the game can communicate.

When the communication cost of a stubborn person is greater than or equal to 8, it is impossible for the stubborn person to establish communication with the game object. Regardless of whether the game object is a rational person or not, the stubborn person's decision will not change. However, after determining the stubborn person's strategy, a rational person cannot change their own strategy. Therefore, the game result is bound to achieve a worse Nash equilibrium. At the same time, due to not changing strategies through communication, stubborn individuals will gain psychological benefits from adhering to the initial strategy, and the benefits obtained by stubborn individuals are higher than those of rational individuals.

Table 2: Payoff of a prisoner's dilemma

4.3. A's payoffs

The Figure 1 shows the function graph of the game strategy of Stone Scissor Cloth and its corresponding strategy. The x coordinate represents the mixed strategy probability of A, and the y coordinate represents the mixed strategy probability of B. Therefore, when one player determines the strategy, the other party will definitely have the corresponding optimal strategy. In the game of two rational people playing rock scissors, the equilibrium point of Nash equilibrium is the probability of both sides averaging out the rock scissors, which is one-third of the probability that most of us will randomly make gestures. Rational individuals with bounded rationality tend to gradually approach the Nash equilibrium point in games.

When rational people deal with stubborn opponents in a game, stubborn players tend to maintain their original strategies, which often leads to them changing their strategies and slowing down their speed towards the equilibrium point. At the same time, the equilibrium point of Nash equilibrium will also shift on the function graph. In this game, compared to facing rational opponents, a rational player can gain greater benefits when playing against stubborn players.

Meanwhile, assuming that the players in this game are two stubborn players, they may not even adopt the best strategy to deal with each other on the function graph when reaching Nash equilibrium.

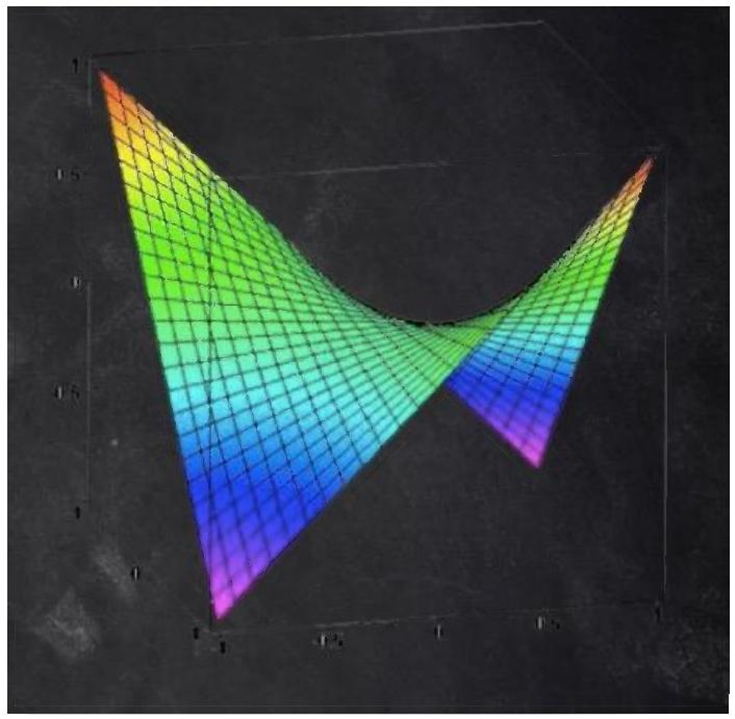
Figure 1: Stereoscopic functional model

5. Discussion

By digitalize all the behaviors of stubborn individuals in games, we can understand their actions in life and empathize with them through understanding. When we no longer consider stubbornness as an unstable factor and instead consider it a very important characteristic, we can discuss its impact more objectively. This paper aims to discuss stubbornness as a true part of nature in this way.

Stubbornness is actually just a natural instinct of humans, and it is due to the theory of adaptive evolution that it is beneficial for our survival and has always influenced us. Through game theory and data-driven methods, we can intuitively understand the role and necessity of stubbornness in our lives. Meanwhile, this also helps us understand human rationality from another perspective: in games, we believe that irrational behavior is actually the optimal solution calculated by others.

In (4,1), by comparison, it can be concluded that when our game is a game that requires cooperation rather than confrontation, as long as our game partner is a stubborn person, regardless of who we are, our profits are likely to be lower than the same situation when our cooperation partner is a rational person. Hong Zhang also mentioned in an article studying the same issue: "Both stub born operators and stub born defects in the evolution of cooperation. Stubborn operators play a prior role in the inhibition of cooperation. The stub born players prevent the expansion of cooperative clusters in different ways." [4]However, when we collaborate, the likelihood of returns being higher when I am a stubborn person than when I am a rational person is higher.

From this, it can be seen that stubbornness in cooperation is often a characteristic that benefits oneself at the expense of others, and there is a chance that it may lead to a decrease in one's own interests. This characteristic is equivalent to sharing the risk of not gaining benefits, but sometimes it also harms one's own interests. It can be said that stubbornness can be associated with conservatism and fear of risk. When a person is neither trusting himself but nor trust others, it is easy to fall into a stubborn mentality. In this situation, I believe that encouragement and positive expression would be a good way to reduce stubbornness in cooperation; At the same time, by adhering to commitments in the game and providing good and correct suggestions, it is also possible to effectively prevent unnecessary stubbornness from the outside world. At the same time, as a stubborn party, one can also trace their stubbornness back to the purpose, distinguish when to let go of their stubbornness, and when to change their strategy. I have observed that when stubborn people encounter them, they are more likely to recognize each other compared to losing both sides. This is because they trust each other and reduce communication costs due to their adherence to strategies. (Reference)

In (4, 2), by controlling variables, we can know that stubbornness is a characteristic that reduces the likelihood of obtaining the optimal solution and ultimately harms the public interest as a whole. In situations similar to the prisoner's dilemma, only multiple games or interest binding can break the fate of both parties losing. In situations where stubborn individuals may lead to reduced communication efficiency, we can solve the prisoner's dilemma through interest binding. Although stubbornness in life may not be completely eliminated through interest binding, this is a more rational approach. If we give up cooperation without calculation due to negative impressions of stubborn individuals, it may actually be a manifestation of stubbornness in us. Meanwhile, from a perspective that goes beyond theory, "A small noise can resist the discriminative effects induced by the stub players." [5]

In (4, 3), we can see that when we are opponents of stubborn individuals in the game, we often gain greater benefits than when we are opponents of rational individuals because we do not fully share our goals. And this is not a win-win situation. From this perspective, we can also say that stubbornness can help us transform many zero sum games into positive sum games. This is also the magic that our hearts need and the mystery of life, which is another evidence that stubbornness, which we have not yet discovered, is beneficial.

In summary, we have learned that as rational individuals, we should respond correctly to stubbornness, or as stubborn individuals, we should make the most of our stubbornness. Meanwhile, we have demonstrated with great certainty that stubbornness is a characteristic that needs to be viewed with a positive perspective.

6. Conclusion

This article aims to explore the application of game theory in psychology, but due to capacity issues, it is not possible to fully utilize mathematical knowledge for calculations and summaries. At the same time, due to the limited introduction of related concepts, there is also limited information available for application.

Introducing mathematical methods into psychology is a good way to conduct practical research on many difficult psychological theories, and I believe it can lead to more professional and scientific development. At the same time, it is necessary to discuss the nature of many people who were originally biased towards us, which can help more people build confidence and build understanding of the world. I believe this is one of the ways psychology benefits humanity.