1.  Introduction

1.1.  Background and significance

1.1.1.  Development and application fields of drone technology

Drones have rapidly evolved from niche gadgets to mainstream tools in the last decade as the manufacturing costs have decreased. Alongside the lower costs, many drone-related technologies have also improved, such as sensors. To adapt to the many different environments in which drones are being used today, flight controllers must be well-tested and exhibit desirable control even under extreme conditions,as shown in Figure 1 and Figure 2.

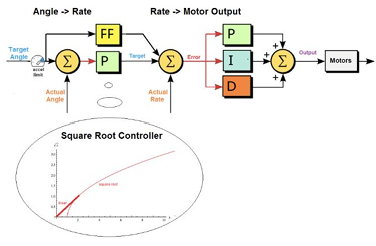
Drones typically consist of an inner loop for stability and control, and an outer loop for high-level tasks, such as navigation. Many algorithms are used to achieve these abilities, such as computer vision-based obstacle avoidance, and AI models for path planning and controls. The inner loop is implemented predominantly with PID. Despite the great performance of PID in stable environments, a different algorithm is definitely needed to navigate a harsher and more unpredictable environment [2].

1.1.2.  Key role of attitude control

A drone’s attitude—its roll, pitch and yaw—is the single variable that separates controlled flight from an uncontrolled tumble: being inherently unstable, the airframe must be re-levelled dozens of times per second to stay upright, and any gust or ground-reflected turbulence only tightens that deadline. The same angles also constitute the machine’s only steering mechanism: every translation order is executed by tilting the airframe just enough to vector part of the thrust, so forward flight demands a few degrees of nose-down pitch while hovering in a crosswind requires an opposite roll into the breeze. Because the human stick commands are therefore fulfilled only to the extent that those micro-tilts are accurate and timely, a well-tuned attitude loop is what ultimately gives the pilot the impression of an obedient, “easy-flying” aircraft that will sit motionless in the sky until the next intentional nudge [3].

1.1.3.  Potential of reinforcement learning in attitude control

Reinforcement learning (RL) treats control as a sequential decision-making problem, where an agent (the drone’s controller) learns a policy by interacting with the environment and receiving feedback in the form of rewards. Unlike traditional model-based approaches, RL is model-free: it does not require an explicit dynamics model. Instead, the system learns an optimal control policy through trial-and-error, optimizing behavior to maximize cumulative rewards. Modern deep RL algorithms use neural networks to handle high-dimensional state inputs and continuous action outputs, making them well-suited for complex drone dynamics [4].

1.2.  Purpose and problem

1.2.1.  Limitations of traditional controllers

Traditional controllers—cascaded PID, LQR or linear MPC—depend on a fixed, low-order model and on an IMU whose drift-prone, noisy outputs must be continuously filtered; they treat the drone as a time-invariant plant and tune gains for a narrow hover envelope. Once mass shifts, rotors age, wind becomes gusty, or the airframe enters aggressive maneuvers, the same gains over- or under-react, excite un-modeled flexible modes, and saturate motors, so performance drops and manual re-tuning is required—an inherent limitation that motivates learning-based, adaptive alternatives [5].

1.2.2.  Applicability of PPO in drone attitude control

PPO (Proximal Policy Optimization) is a learning-based controller. Instead of hand-tuning gains or relying on a fixed model, PPO learns a policy—a mapping from the drone’s state (angles, rates, etc.) to motor commands—by practice (usually in simulation first). During training, it tries many actions, sees what works, and improves step by step. PPO adds a simple safety idea to training: only allow small, careful policy updates each round, which keeps learning stable [6].

It's particularly suitable for drone attitude control for the following reasons:

1. The drone’s true behavior changes with battery voltage, prop damage, wind, and payload. PPO doesn’t need a perfect model; it learns how to react from experience, including tricky cases (e.g., wind, ground effect), so it can handle nonlinear and changing dynamics naturally.

2. Instead of tuning KP, KI, KD (the values for a PID controller) by hand, you design a reward that encodes what you care about (small angle error, low rates, smoothness, low power). PPO then tunes itself to balance those goals. That makes it easier to target multiple objectives at once.

3. When you train in simulation with varied conditions (different masses, winds, sensor noise), PPO learns a single policy that works across them. This “practice on many scenarios” often yields robust behavior without per-scenario gain tables.

4. PPO can take in many signals at once (attitude, rates, motor temps, vibration metrics). Classical loops typically use a few signals and assume the rest is constant/insignificant. PPO can learn to weigh these inputs to make better choices.

1.2.3.  Points of innovation

First, I adopted Reinforcement Learning algorithm (PPO) in drone attitude control to achieve better stability than traditional PID and LQR controllers, without spending too much extra computation budget.

Second, rather than report error only, I measured actuator command distribution and second-moment statistics to show that PPO achieves improved stability without unreasonable actuation spikes (smooth overall action instead of sudden twitches that minimizes error).

2.  PPO algorithm

2.1.  Core principals and mathematical derivation of PPO

TRPO derives a theory-backed update rule that contains each policy step using a KL-divergence-based trust region, yielding conservative updates with monotonic improvement guarantees. In practice, however, directly penalizing the KL term can be overly stringent and lead to very small steps unless the penalty weight is carefully tuned. Moreover, a single penalty coefficient that works across tasks, or even across phases of training on the same task, can be hard to pick [7].

A useful way to describe the KL-penalized step is:

$$ {\text{∆}\text{θ}}^{\text{∗}}\text{=}\text{arg}\underset{\text{Δ}\text{θ}}{\text{max}}{\text{L}}_{\text{θ}\text{+Δ}\text{θ}}\text{−}\text{β}{\text{D}}_{\text{KL}}\left({\text{π}}_{\text{θ}}\Vert {\text{π}}_{\text{θ}\text{+Δ}\text{θ}}\right)$$(1)

where  $$ \text{L}$$  is the policy gradient term and  $$ \text{β}\text{>0}$$  is the KL penalty coefficient. The central difficulty is choosing  $$ \text{β}$$ so that updates are neither too timid nor aggressive.

With PPO, one widely used variant (PPO Clip) replaces the explicit KL penalty with a clipped probability-ratio objective. Let

$$ {\text{r}}_{\text{t}\left(\text{θ}\right)}\text{=}\frac{{\text{π}}_{\text{θ}\left({\text{a}}_{\text{t}}|{\text{s}}_{\text{t}}\right)}}{{\text{π}}_{{\text{θ}}_{\text{old}}}\left({\text{a}}_{\text{t}}|{\text{s}}_{\text{t}}\right)}$$(2)

 $$ {\widehat{\text{A}}}_{\text{t}}$$ an advantge estimate and choose a small clipping hyper-parameter $epsilon$. The clipped surrogate is

$$ {\text{L}}_{\text{clip}}\left(\text{θ}\right)\text{=}\text{E}\left[\text{min}\left({\text{r}}_{\text{t}\left(\text{θ}\right)}{\widehat{\text{A}}}_{\text{t}}\text{,}\text{clip}\left({\text{r}}_{\text{t}\left(\text{θ}\right)}\text{,1−}\text{ε}\text{,1+}\text{ε}\right){\widehat{\text{A}}}_{\text{t}}\right)\right]$$(3)

if  $$ {\text{r}}_{\text{t}}$$  tries to move outside of  $$ \left[\text{1−ε,1+ε}\right]$$ , the term is surrogated, so pushing further gives no extra improvement in the objective (the gradient contribution vanishes in those regions). Intuitively, positive advantage actions can only be up-weighted to about  $$ \text{1+ε}$$  times their old probability, and negative actions can only be down-weighted to about  $$ \text{1−ε}$$ . This prevents oversize policy jumps while still permitting meaningful changes. The original PPO paper shows that clipping yields a conservative lower bound on the unconstrained objective.

PPO clipped is generally preferred as it's much easier to implement while still maintaining trust region like behavior. The original study also found PPO clipped to be more stable and generally better-performing than PPO penalty (another variant that relies on an adaptive KL penalty, but due to relevance, I will not go too deep into how it works) across multiple benchmarks [8].

2.2.  Construction and optimization of objective function

Within PPO, the objective function is commonly a clipped function, to control the steps of policy updates.

$$ {\text{L}}_{\text{clip}}\left(\text{θ}\right)\text{=}\text{E}\left[\text{min}\left({\text{r}}_{\text{t}\left(\text{θ}\right)}{\widehat{\text{A}}}_{\text{t}}\text{,}\text{clip}\left({\text{r}}_{\text{t}\left(\text{θ}\right)}\text{,1−}\text{ε}\text{,1+}\text{ε}\right){\widehat{\text{A}}}_{\text{t}}\right)\right]$$(3)

where,  $$ {\text{r}}_{\text{t}\left(\text{θ}\right)}\text{=}\frac{{\text{π}}_{\text{θ}\left({\text{a}}_{\text{t}}|{\text{s}}_{\text{t}}\right)}}{{\text{π}}_{{\text{θ}}_{\text{old}}}\left({\text{a}}_{\text{t}}|{\text{s}}_{\text{t}}\right)}$$  is the probability,  $$ {\widehat{\text{A}}}_{\text{t}}$$  is the advantage estimate,  $$ \text{ε}$$  is the super parameter for the clipping region. This objective function guarantees the steps taken won't be overly aggressive, which improves stability.

Update the policy parameters $theta$ by performing gradient ascent to maximize the clipped objective. At each update, compute the policy loss  $$ {\text{L}}_{\text{clip}}\left(\text{θ}\right)$$ , then use backpropagation to obtain the gradients and apply an optimizer to update the parameters of the policy network.

Objective Function Construction and Optimization process for Value Function Update

The goal of updating the value function is to make its predictions as close as possible to the ground truth values. This is typically achieved by minimizing the mean squared error between the predicted value and the actual target. Specifically, the optimization objective for the value function is:

$$ {\text{L}}_{\text{VE}}\left(\text{θ}\right)\text{=}{\text{E}}_{\text{t}\left[{\left({\text{V}}_{\text{θ}}\left({\text{s}}_{\text{t}}\right)\text{−}{\text{V}}_{\text{target}}\left({\text{s}}_{\text{t}}\right)\right)}^{\text{2}}\right]}$$(4)

where  $$ {\text{V}}_{\text{target}}\left({\text{s}}_{\text{t}}\right)$$  is the target value, often computed using a smoothed advantage estimate. The value-function parameters  $$ \text{φ}$$  are then updated by gradient descent to minimize this mean squared error loss at every step.

3.  Application and design of PPO in drone attitude control

3.1.  Experimental environment

In this project, I have chosen the CQ230 Open Source Drone Development Kit as our platform. This kit combines a Raspberry Pi 4B with a Pixhawk 2.4.8 flight controller (FC) to form a compact quadrotor. The Pixhawk FC runs the open source ArduPilot firmware, while the Raspberry Pi hosts development tools. Together, these features make the CQ230 kite ideal for my project [9].

3.1.1.  Overall setup

The drone design comprises two main aspects: the structural design and the electrical design. The CQ230 kit provides all necessary hardware components, allowing us to focus primarily on algorithm implementation and system integration.

3.1.2.  Structural design

The CQ230 drone kit uses a custom designed anti-collision frame as its structural backbone,as shown in Figure 3.

The frame has a 230 mm diagonal motor spacing in a symmetric quadcopter layout. The overall dimensions are approximately 350 by 360 by 300 mm, and the fully assembled weight is around 612 grams. This compact, lightweight design enables operation in confined, indoor spaces. In summary, the CQ230’s structural design balances miniaturization and robustness, providing a reliable hardware foundation for our experiments.

3.1.3.  Hardware

All hardware used in the project is listed in Table 1.

Table 1. Hardware

Name	Image	Description
Pixhawk 2.4.8 Flight Controller		Acts as the drone’s brain. It features a 32-bit STM32F427 processor, an onboard BMP561 barometer, and multiple I/O ports.
Raspberry Pi 5B		Serves as the companion computer, running Ubuntu with pre-installed libraries. It handles high-level tasks such as computer vision, path planning, and network communication.
Brushless Motors (2205)		Four 2205-series brushless motors paired with 5045 propellers deliver thrust and maneuverability.
Electronic Speed Controllers (30 A ESC)		Each motor is controlled by a 20 A ESC, which receives PWM signals from the Pixhawk and precisely regulates motor RPM.
Battery (4S, 16.8V 2300 mAh)		A single 4S battery provides enough power to sustain 7 minutes of flight.
Power Module (Ledi Mini Pix)		Distributes battery power to the FC and provides voltage/current telemetry back to the FC for low-voltage warnings and failsafe logic.
Optical Flow Sensor (MF-01)		Combines a downward-facing optical flow camera with a laser/ultrasonic rangefinder to provide position and height feedback.
GPS Module (Ublox M8N)		Provides outdoor GNSS positioning with 2-3 m horizontal accuracy.
RC Transmitter/Receiver (FlySky FS-i6)		A 6-channel 2.4 GHz transmitter and receiver allow manual control during testing and a range up to 700 meters.
Buzzer (BB Alarm Buzzer)		Signals various flight events through audible alerts.

3.1.4.  Software environment and simulation setup

Operating system: On the drone, a Raspberry Pi 5B is used, with Ubuntu 24 installed, combined with Pixhawk to realize the control of the drone.Ground station uses: Windows + Anaconda + PyCharm/VScode.Programming language and toolchain: Python is used for the development of the PPO algorithm, and reinforcement learning libraries such as Stable-Baselines3 are used to accelerate implementation.Simulation platform: A UAV dynamics simulation environment based on PyBullet is constructed for algorithm training and preliminary verification.

3.2.  Reinforcement learning framework design

3.2.1.  Action space and state space definition

The action space A is defined as:

$$$ \text{A}\text{=}\left[\text{Δ}{\text{ω}}_{\text{1}}\text{,Δ}{\text{ω}}_{\text{2}}\text{,Δ}{\text{ω}}_{\text{3}}\text{,Δ}{\text{ω}}_{\text{4}}\right]$$$

where:

•  $$ \text{Δ}{\text{ω}}_{\text{1}}\text{,Δ}{\text{ω}}_{\text{2}}\text{,Δ}{\text{ω}}_{\text{3}}\text{,Δ}{\text{ω}}_{\text{4}}$$ represent the variations in the rotational speeds of the four motors.

• The range of rotational speed variation is  $$ \left[\text{−0.08,0.08}\right]$$ , expressed in terms of relative changes in rotational speed. This formulation facilitates exploration and learning for the reinforcement learning algorithm.

def __init__(self):

super(DroneGymEnv, self).__init__()

self.state_dim = 15

self.state_space = Box(low=-np.inf, high=np.inf, shape=(self.state_dim,), dtype=np.float32)

self.action_dim = 4

self.action_space = Box(low=-0.08, high=0.08, shape=(self.action_dim,), dtype=np.float32)

3.2.2.  Reward function

The design of the reward function is crucial for the performance of reinforcement learning algorithms. In the task of attitude stabilization control of drones, the reward function $R$ is defined as:

$$$ \text{R}\text{=}\text{α}{\text{R}}_{\text{1}}\text{+}\text{β}{\text{R}}_{\text{2}}\text{+}\text{γ}{\text{R}}_{\text{3}}\text{+}\text{δ}{\text{R}}_{\text{4}}\text{+}\text{ε}{\text{R}}_{\text{5}}$$$

•  $$ {\text{R}}_{\text{1}}$$ : Positional deviation reward: $$ {\text{R}}_{\text{1}}\text{=−}\left|\text{x}\text{−}{\text{x}}_{\text{target}}\right|\text{−}\left|\text{y}\text{−}{\text{y}}_{\text{target}}\right|\text{−}\left|\text{z}\text{−}{\text{z}}_{\text{target}}\right|$$ 

•  $$ {\text{R}}_{\text{2}}$$ : Velocity reward: $$ {\text{R}}_{\text{2}}\text{=−}\left|{\text{v}}_{\text{x}}\right|\text{−}\left|{\text{v}}_{\text{y}}\right|\text{−}\left|{\text{v}}_{\text{z}}\right|$$ 

•  $$ {\text{R}}_{\text{3}}$$ : Attitude reward: $$ {\text{R}}_{\text{3}}\text{=−}\left|\text{θ}\right|\text{−}\left|\text{φ}\right|\text{−}\left|\text{ψ}\right|$$ 

•  $$ {\text{R}}_{\text{4}}$$ : Angular velocity reward: $$ {\text{R}}_{\text{4}}\text{=−}\left|{\text{ω}}_{\text{x}}\right|\text{−}\left|{\text{ω}}_{\text{y}}\right|\text{−}\left|{\text{ω}}_{\text{z}}\right|$$ 

•  $$ {\text{R}}_{\text{5}}$$ : Control effort reward: $$ {\text{R}}_{\text{5}}\text{=−}\left|\text{Δ}{\text{F}}_{\text{1}}\right|\text{−}\left|\text{Δ}{\text{F}}_{\text{2}}\right|\text{−}\left|\text{Δ}{\text{F}}_{\text{3}}\right|\text{−}\left|\text{Δ}{\text{F}}_{\text{4}}\right|$$ 

Here,  $$ \text{α,β,γ,δ,ε}$$  are the weighting coefficients. Their relative weighting is set such that:

$$$ \text{γ>α,β,δ>ε}$$$

which ensures attitude stability is prioritized.

def _calculate_reward(self, state, action):

x, y, z, v_x, v_y, v_z, pitch, roll, yaw, omega_x, omega_y, omega_z, wind_x, wind_y, wind_z = state

delta_omega1, delta_omega2, delta_omega3, delta_omega4 = action

r_position = - (abs(x) + abs(y) + abs(z))

r_velocity = - (abs(v_x) + abs(v_y) + abs(v_z))

r_attitude = - (abs(pitch) + abs(roll) + abs(yaw))

r_angular_velocity = - (abs(omega_x) + abs(omega_y) + abs(omega_z))

r_action = - (abs(delta_omega1) + abs(delta_omega2) + abs(delta_omega3) + abs(delta_omega4))

reward = 0.1 * r_position + 0.2 * r_velocity + 0.3 * r_attitude + 0.3 * r_angular_velocity + 0.1 * r_action

return reward

In the experiments, the weighting parameters will be tuned according to the specific tasks and environmental conditions of the drone, in order to achieve optimal control performance. The reward function is designed to comprehensively account for the drone’s position, velocity, attitude, angular velocity, and control effort, thereby guiding the drone toward stable flight in complex environments.

3.2.3.  Model evaluation

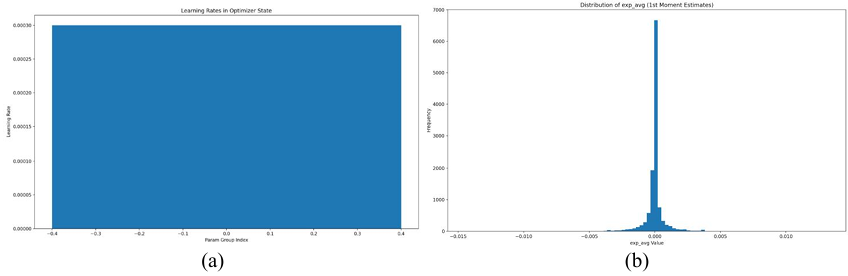
Figure 4(a) illustrates the distribution of learning rates across different parameter groups in the optimizer. It can be observed that all parameter groups share a constant learning rate of  $$ \text{0.0003}$$ , indicating that the optimizer adopts a unified learning rate strategy. Such a configuration helps maintain convergence and stability during training, preventing instability that may arise from large discrepancies in learning rates. The choice of  $$ \text{0.0003}$$  was based on preliminary hyper parameter tuning experiments, where this value consistently delivered good performance—striking a balance between rapid convergence and avoiding oscillations caused by excessively large update steps. Future work may explore dynamic learning rate adjustment strategies, such as learning rate decay or adaptive learning rate methods, to achieve better performance across different training stages.

Figure 4(b) shows the histogram of the frequency distribution of exp_avg values, where the horizontal axis represents the exp_avg values and the vertical axis represents frequency. The results indicate that most exp_avg values are concentrated around zero, forming a sharp peak. This distribution suggests that the algorithm tends to reduce the magnitude of policy updates during training, thereby promoting more stable policy improvement. The sharpness of the distribution also implies relatively low variance in updates, which benefits learning efficiency and stability. However, such a distribution may limit the algorithm’s ability to explore new strategies, since most update steps are small. Future research may focus on balancing exploration and exploitation to enhance adaptability and flexibility in more complex environments.

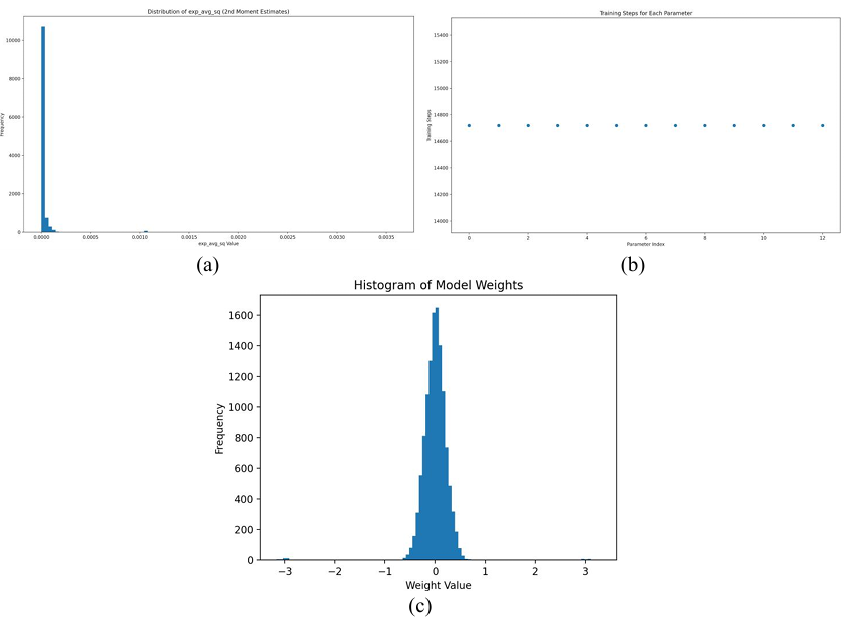
Figure 5(a) presents the histogram of the frequency distribution of exp_avg_sq values. The results show an even sharper concentration around zero, with nearly all estimates clustered extremely close to zero. This highly concentrated distribution indicates effective control over the second-moment estimates of policy updates, which likely helps reduce variance in updates and further improves training stability.

Figure 5(b) depicts the number of training steps corresponding to each parameter index. The data reveal that all parameters were updated at a relatively stable rate of approximately  $$ \text{14700}$$  steps, suggesting balanced updates across all model parameters. Such uniformity ensures that every parameter receives sufficient training, thereby preventing under-trained parameters from degrading overall model performance.

In this setup, the total number of time steps was set to  $$ \text{95000}$$ , with a fixed learning rate of $0.0003$ to ensure stable learning. The discount factor was set to  $$ \text{0.99}$$  to balance the importance of immediate and future rewards. For variance reduction and bias improvement, we adopted the Generalized Advantage Estimator (GAE) with  $$ \text{λ = 0.95}$$ . The entropy coefficient was set to 0 to avoid encouraging randomness during training, while the value function coefficient was set to  $$ \text{0.5}$$  to balance updates between policy and value function. To prevent gradient explosion, the maximum gradient norm was clipped at  $$ \text{0.5}$$ . Each training iteration used a batch size of  $$ \text{64}$$ , with  $$ \text{10}$$  epochs per update. Finally, the clipping range of PPO was set to  $$ \text{0.2}$$ , limiting policy update magnitude to further enhance training stability.

Figure 5(c) reveals that the weight values are primarily concentrated around zero and approximately follow a normal distribution, with the highest frequency occurring between  $$ \text{−1}$$  and  $$ \text{1}$$ . This distribution indicates that the model weights were effectively regularized during training, which helps prevent overfitting and improves generalization. Moreover, maintaining a well-balanced weight distribution is crucial for model performance and stability, since excessively large or small weights can lead to overfitting or underfitting.

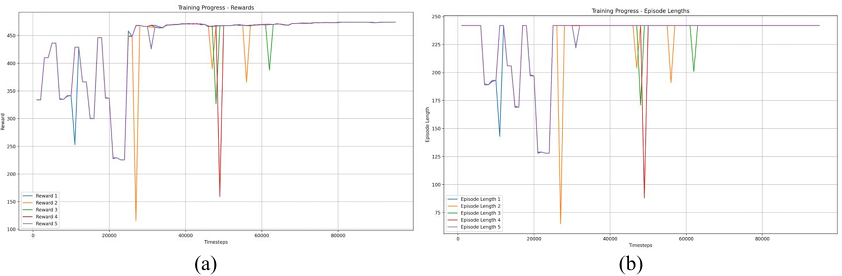
PPO training exhibits an early exploratory phase followed by convergence; Reward  $$ \text{1}$$  and Reward  $$ \text{5}$$  dominate in magnitude and stability ( $$ \text{≈450}$$ ) in later training, indicating their primary role in optimizing drone attitude stabilization, while other reward terms contribute less,as shown in Figure 6.

Episode lengths show high variability during exploration but converge to stable values across all five episode types as training proceeds, indicating policy maturation and consistent task performance.

3.3.  Experimentation

3.3.1.  Simulation verification

^* There are more levels, but for the purposes of this research, up to level 5 is enough.

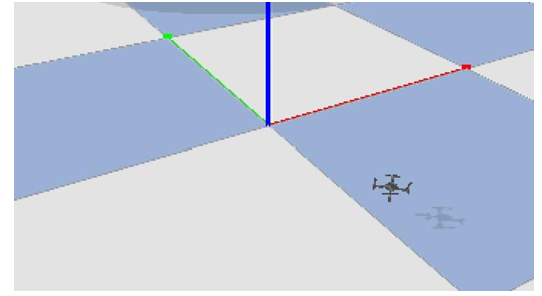
To comprehensively evaluate the performance of Proximal Policy Optimization (PPO) versus a conventional PID controller for drone attitude stabilization, we conducted a set of simulation experiments in the PyBullet environment. Simulations covered a range of wind conditions from Beaufort-scale equivalent level  $$ \text{0}$$  to level  $$ \text{5}$$  (approximately  $$ \text{0}$$  to  $$ \text{8.0}$$  m/s),as shown in Table 2. For each wind condition we recorded key performance metrics, including attitude angles (pitch, roll, and yaw), position error, angular velocities, and control command magnitudes. These measurements were used to quantify stability, tracking accuracy, control effort, and robustness to aerodynamic disturbance,as shown in Figure 7 and Figure 8.

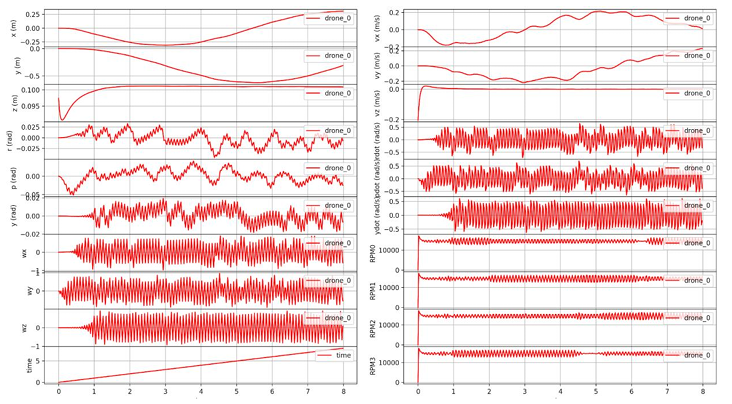
In simulations with progressively increasing wind speed, the PPO controller exhibited superior attitude stability. Even under strong winds equivalent to Beaufort scale  $$ \text{5}$$  ( $$ \text{≈8.0}$$  m/s), attitude deviations remained within  $$ \text{±5°}$$ , whereas the PID controller’s attitude excursions under the same conditions expanded to approximately  $$ \text{±15°}$$ . This indicates that PPO substantially improves disturbance rejection and reduces the accumulation of attitude error in adverse aerodynamic conditions,as shown in Figure 9.

Position-error measurements further confirm PPO’s advantage. Across wind levels, the PPO-controlled vehicle maintained lower position deviations. For example, under level-3 winds ( $$ \text{≈3.4−5.4}$$  m/s), the mean position error with PPO was only  $$ \text{0.8}$$ m, compared with  $$ \text{1.5}$$ m for PID control. This improvement is attributable to PPO’s capacity for timely corrective actions and more precise compensation for wind disturbances, enabling the vehicle to track the target position more closely during gusty flight.pics/experiment_materials.png

3.3.2.  Physical experimentation

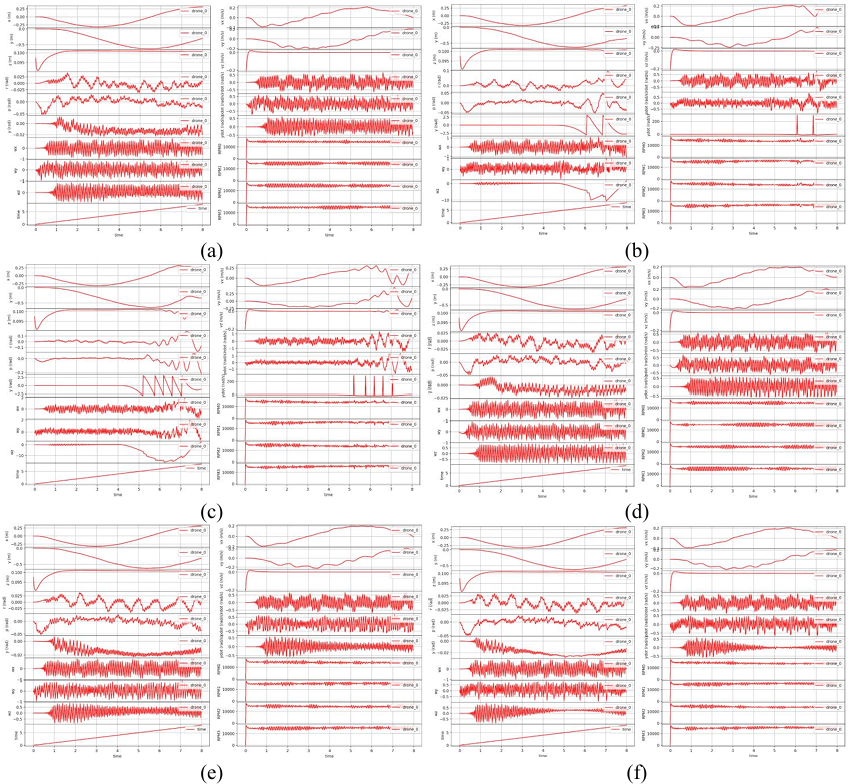
Due to environmental constraints and the power limitations of household fans, the UAV state under level-3 wind conditions,as shown in Figure 10.

Figure 11. (a)Attitude angle of PID at Level 0 wind. (b) Attitude angle of PID at level 3 wind. (c)Attitude angle of PPO at level 3 wind

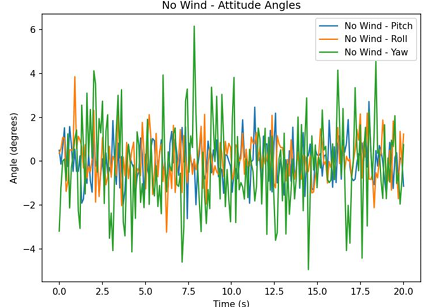
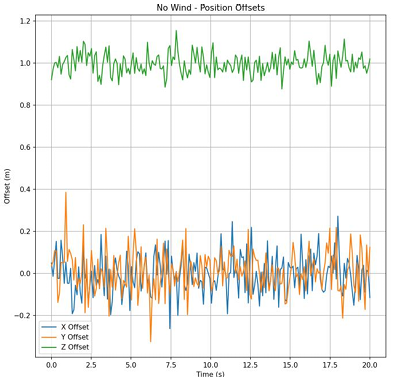
Under no-wind conditions, the drone’s horizontal displacements in both the X and Y axes were tightly regulated, with mean values effectively zero and a standard deviation of approximately  $$ \text{0.10}$$ m,as shown in Figure 11. Altitude was held stably at the  $$ \text{1.0}$$ m setpoint with only minor fluctuations (standard deviation $$ \text{≈0.5}$$ m). Under natural level-3 winds, the horizontal displacement variability increased markedly: the standard deviation in X and Y rose to  $$ \text{≈0.3}$$ m, indicating degraded position stability; altitude remained centered on  $$ \text{1.0}$$  m but with an increased standard deviation of  $$ \text{≈0.10}$$  m. When controlled by the reinforcement-learning (PPO) controller, however, the drone’s positional performance under level-3 winds improved substantially: horizontal displacement standard deviations were reduced to  $$ \text{≈0.15}$$ m in both X and Y, and altitude fluctuation was constrained to a standard deviation of  $$ \text{≈0.07}$$ m. These results demonstrate the superiority of the learned controller in maintaining precise position and altitude in moderately windy conditions, reinforcing its suitability for disturbance-robust drone operation.

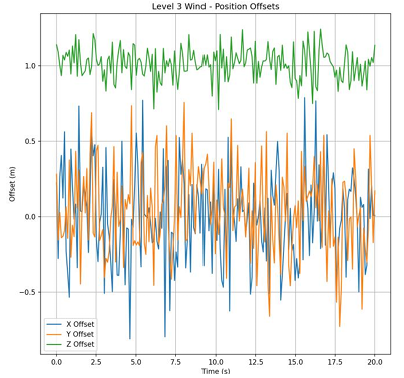
Figure 12. (a) Positional offset of PID at level 0 wind. (b) Positional offset of PID at level 3 wind. (c) Positional offset of PPO at level 3 wind

With no wind, the drone's  $$ \text{x}$$  and  $$ \text{y}$$  displacements were tightly regulated, with mean values effectively  $$ \text{0}$$  and a standard deviation of approximately  $$ \text{0.1}$$ m,as shown in Figure 12. Altitude was held stably at the  $$ \text{1.0}$$ m setpoint with minor fluctuations (standard deviation  $$ \text{≈0.5}$$ m). When exposed to natural level-3 wind, horizontal variability increased. The standard deviation in  $$ \text{x}$$  and  $$ \text{y}$$  rose to around  $$ \text{0.3}$$ m, indicating degraded lateral position stability; altitude remained centered on  $$ \text{1.0}$$ m, but with a increased standard deviation of about  $$ \text{0.1}$$ m. By contrast, the reinforcement-learning controller substantially mitigated these disturbances. Under the same level-3 wind,  $$ \text{x}$$  and  $$ \text{y}$$  standard deviation were reduced to approximately  $$ \text{0.15}$$ m, and altitude variability was constrained to a standard deviation of  $$ \text{0.07}$$ m. These results highlight the learned controller's superior ability to provide precise positional regulation in moderately windy conditions and demonstrate its potential to improve disturbance-robust operation [10].

4.  Conclusion and outlook

4.1.  Summary of research results

This study compared a learned controller (PPO) against a conventional cascaded PID baseline for attitude stabilization and position holding on a small quadrotor platform (CQ230-style hardware in simulation). Key findings are:

• Attitude stability under wind. In progressively stronger simulated winds PPO maintained attitude excursions within  $$ \text{±5°}$$  at  $$ \text{≈8.0}$$ m/s, whereas the tuned PID’s excursions grew to roughly  $$ \text{±15°}$$  under the same conditions.

• Position accuracy. Under level-3 winds ( $$ \text{≈3.4−5.4}$$ m/s) the PPO policy produced a mean position error of  $$ \text{~0.8}$$ m versus  $$ \text{~1.5}$$  m for PID; horizontal displacement standard deviations improved from  $$ \text{~0.30}$$ m under PID to  $$ \text{~0.15}$$ m under PPO. Altitude variability also reduced from  $$ \text{≈0.10}$$ m with PID to  $$ \text{≈0.07}$$ m with PPO.

• Practical observation. PPO’s advantage stems from its ability to (1) implicitly learn nonlinear compensation for wind and actuator effects, (2) optimize multi-objective trade-offs encoded in the reward, and (3) generalize across a range of simulated disturbances when trained with sufficient scenario variety.

These results demonstrate that reinforcement learning, when carefully trained, can improve robustness and stability for small consumer drones relative to traditional control tuned around a single operating point.

4.2.  Deficiencies and future work

All experiments used simulated wind (PyBullet) and household-fan test with limited uniformity and power. The learned policy may not directly transfer to physical hardware without domain randomization, system identification, or real-world fine tuning. Also, the simulator and the household wind setup do not fully reproduce turbulent, spatially varying wind fields, ground effect, or detailed propeller aerodynamics. These unmodeled effects can degrade real-world performances of PPO [11].

Also, due to using Reinforcement Learning Algorithms, important safety behaviors require additional verification, fallback controllers (which still have to be tuned), or runtime monitors. Also, training required many interactions: on-board learning or frequent re-training is impractical unless sample efficiency improves or efficient online adaptation schemes are implemented. Additionally, deploying neural network policies onboard requires attention to latency, quantization, and computational power on embedded platforms. Performance depends strongly on reward engineering. Learned behaviors can be brittle if reward terms are misaligned. Interpreting why a learned policy behaves a certain way also remains difficult. Experiments covered a finite set of wind magnitudes and conditions. Generalization to all other payloads, motor faults, and extreme maneuvers was not evaluated, and therefore lead to degraded performances in those scenarios [12].

Therefore, some suggested next steps includes:

• Add domain randomization (mass, sensor noise, delay, wind patterns) and system identification to narrow simulation-to-real gap.

• Explore more hybrid architectures (such as PPO with PID/LQR as fallback) in the case of PPO failure.

• Investigate explainability tools and systematic ablation studies to better understand reward-term contributions.